Главная
Лекция 10. Исследование колебаний механических систем.
В данной лекции рассматриваются следующие вопросы:
1. Основные определения колебательного движения.
2. Малые свободные колебания системы.
3. Свободные колебания системы с учетом сил
сопротивления движению.
4. Вынужденные колебания системы.
5. Влияние сопротивления на вынужденные колебания.
Изучение
данных вопросов необходимо для изучения колебательных движений механической
системы в дисциплине «Детали машин», для решения задач в дисциплинах «Теория
машин и механизмов» и «Сопротивление материалов».
Основные определения колебательного движения.
Колебательным движением материальной системы называется такое ее движение, при котором она через некоторые
промежутки времени постоянно возвращается к определенному положению.
Нетрудно обнаружить, что большинство окружающих нас
систем совершают колебательное движение.
Если время, за которое все точки системы возвращаются
к любому определенному положению с равными скоростями, постоянно и одинаково,
то такое время Т называется периодом колебаний. А эти
колебания – периодическим колебательным движением.
На рис.1 показан пример изменения какой-то обобщенной
координаты q при довольно сложном колебательном процессе. А на рис.2 – при
более организованных, периодических колебаниях.
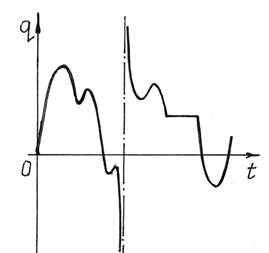
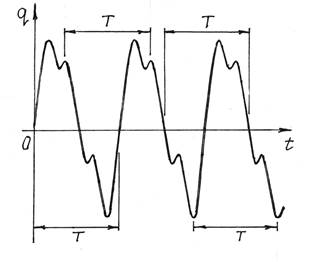
Рис.1 Рис.2
При периодическом процессе значения функции,
описывающей движение системы, повторяются через каждый период Т, т.е.
q(t)=q(t+T). (1)
Если эта функция имеет вид
, (2)
то такое колебательное движение называется гармоническим. График такого
движения дан на рис.3.
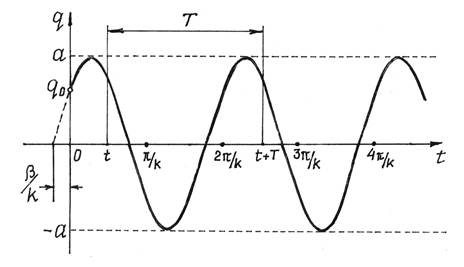
Рис.3
По (2) 
– начальная
координата, определяющая положение системы в начале движения;
A – амплитуда колебаний, имеет размерность обобщенной
координаты;
– фаза
колебаний, 
– начальная
фаза;
k – частота колебаний,
размерность ее с-1.
Период колебаний найдем
используя свойство (1):
Отсюда, т.к. период синуса равен 
, 
. Значит,
период колебаний
Вообще, существует много всяких типов колебаний. Выделим,
в первую очередь, линейные и нелинейные колебания. Названия их определяются
видом дифференциальных уравнений, которые описывают колебательное движение
материальной системы.
Исследование нелинейных колебаний значительно
усложняется, т.к. нет общих методов решения нелинейных дифференциальных
уравнений.
Но, если рассматривать малые колебания, такие, при
которых координата и скорость изменяются на малую величину, то многие
нелинейные уравнения станут линейными и исследование движения значительно упростится.
В дальнейшем мы будем рассматривать лишь малые,
линейные колебания. И, мало того, колебания системы только с одной степенью
свободы.
Естественно, колебания системы могут совершаться
только около устойчивого положения равновесия.
Если система консервативная, то найти положение
равновесия и определить устойчивость его можно с помощью потенциальной энергии.
Ранее было установлено, что в положении равновесия
выполняется условие 
и если в
положении равновесия 
, то равновесие будет устойчиво.
Договоримся отсчитывать координату от положения
равновесия 
а потенциальную
энергию там считать равной нулю (П0=0)
Тогда, по определению малых колебаний, обобщенная координата q всегда
будет малой величиной.
Разложим потенциальную энергию в ряд Маклорена около положения равновесия:
Так как П(0) = 0 и 
и, отбросив
члены третьего и выше порядка малости, получим
, (4)
где коэффициент 
по условию
устойчивости.
Поэтому потенциальная энергия колебательной системы,
отсчитываемая от положения устойчивого равновесия, будет всегда положительной.
Кинетическую энергию системы при малых колебаниях
также можно преобразовать.
Кинетическая энергия системы 
,
а так как радиус-вектор точек 
и
q=q(t), то 
Поэтому 
, где 
Эту функцию A(q) можно разложить в ряд Маклорена
по степеням q около положения равновесия и учесть только первый
член: A(q)=A(0)+… .
Остальные члены можно не учитывать, т.к. после подстановки A(q) в Т, они станут величинами третьего и выше порядка.
Обозначив постоянную A(0)=a получим
T=aq2/2. (5)
Коэффициент a называется
коэффициентом инерции. Конечно, a>0 т.к. кинетическая энергия не может быть
отрицательной.
Замечание.
Практически, при исследовании конкретных колебательных систем приходится
раскладывать в ряд функции, содержащие, чаще всего, sinx, cosx, ex.
Разложение их с точностью до малых второго порядка известны: sinx=x, cos=1-x2/2, ex=1+x+x2/2.
Малые свободные колебания системы.
Свободными колебаниями называется колебательное
движение системы, выведенной из положения равновесия и предоставленной самой
себе.
Составим уравнение Лагранжа для консервативной
системы:
Используя (4) и (5), получим дифференциальное
уравнение свободных колебаний 
или, обозначив c/a=k2,
=0. (6)
Решение этого однородного линейного дифференциального
уравнения второго порядка с постоянными коэффициентами известно:
q=C1coskt+C2sinkt (7)
или, использовав другие
постоянные 
и 
,
. (8)
Следовательно, малые свободные колебания –
гармонические колебания, причем амплитуда колебаний и начальная фаза
определяются начальными условиями (q и 
при t = 0), а частота колебаний k и период Т не зависят от начальных условий, определяются
только конструкцией системы.
Обычно частоту колебаний находят сравнением
полученного дифференциального уравнения с уравнением (6).
Пример 1. Тело весом Р
подвешено на нити,
перекинутой через блок и
прикрепленной к пружине (рис.4). Вес блока G, радиус - r; жесткость пружины с. Определим период
свободных колебаний системы.
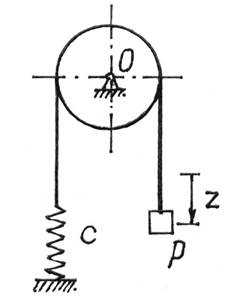
Рис.4
Назначим обобщенной координатой смещение z груза по вертикали от положения
равновесия, при котором пружина была растянута на величину f.
Тогда потенциальная энергия относительно положения
равновесия 
. Где (z+f) - полная
деформация пружины, а cf2/2 -
потенциальная энергия пружины в положении
равновесия, которую вычитаем
из потенциальной энергии полностью деформированной пружины. Раскрыв
скобки, получим
В положении равновесия должно выполняться условие 
. Отсюда P=cf,
значит, П=cz2/2
Кинетическая энергия системы
Составив уравнение Лагранжа, получим 
или 
Сравнивая с (6), находим
частоту колебаний 
и затем период 
Свободные колебания системы с учетом сил
сопротивления движению.
Известно, что свободные колебания не длятся очень
долго. Как правило они, как говорят, затухают и
довольно скоро. Причиной этому является чаще всего – сопротивление среды, в
которой движутся части колебательной системы.
Обычно считают это сопротивление пропорциональным
скорости. Пусть на каждую точку материальной системы действует сила
сопротивления 
. Обобщенная сила, соответствующая этим силам,
Скорость
точек
так как 
– сложная функция, 
а q=q(t). Поэтому 
Значит, 
Обозначим 
. Тогда обобщенная сила сопротивления 
Заметим, что по форме эта функция Ф аналогична кинетической энергии Т. Поэтому, если разложить ее в ряд Маклорена и учесть члены лишь второго порядка малости,
результат получится тоже аналогичным (5): 
(коэффициент b также будет положительным). И тогда
обобщенная сила сопротивления движению
Функция Ф называется диссипативной или функцией
рассеивания энергии системы.
После подстановки в уравнение Лагранжа 
, получим дифференциальное уравнение 
или
(10)
Где n=b/2a - коэффициент
сопротивления, 
- частота
свободных колебаний без сопротивления.
Найдем решение уравнения (10). Характеристическое
уравнение: z2+2nz+k2=0 Корни его 
, могут быть и комплексными, и вещественными в
зависимости от сопротивления, от величины коэффициента n.
а) Случай малого сопротивления (n < k).
Корни получаются комплексными 
, где 
, 
. Решение дифференциального уравнения ищем в виде
(11)
или
(12)
где постоянные C1 и C2 или 
и 
находятся по
начальным условиям.
Сравнивая решение (12) с (2), делаем вывод, что это будут
колебания, но не гармонические, так как амплитуда колебаний, равная 
, не постоянная, уменьшается с течением времени.
Поэтому такие колебания и называются затухающими.
График таких колебаний дан на рис. 5.
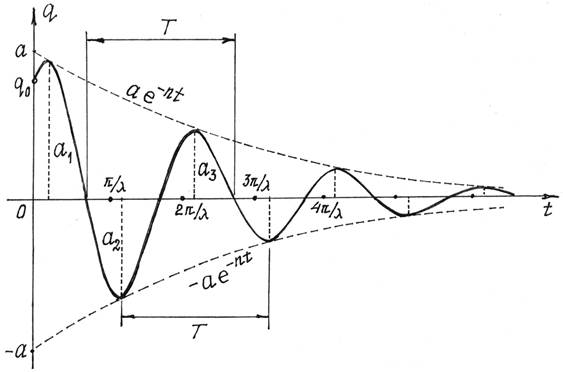
Рис.5
Следует заметить, что колебательный процесс не будет
периодическим. Но, так как система проходит через положение равновесия через
равное время, все-таки вводят понятие периода 
.
Если сравнить этот период колебаний с периодом
колебаний системы без сопротивления (3), увидим, что сопротивление увеличивает
период колебаний и уменьшает их частоту.
Интересна закономерность изменения амплитуды. Найдем
отношение соседних амплитуд (через полпериода T/2):
То есть амплитуды уменьшаются по закону геометрической
прогрессии, знаменателем которой является величина 
.
Натуральный логарифм ее, равный nT/2, называется логарифмическим декрементом колебаний.
Конечно, через период амплитуда уменьшится в 
раз, а через m периодов – в 
раз.
б) Случай большого сопротивления (n>k).
Корни характеристического уравнения получатся
вещественными: . В этом случае, как известно из курса математики,
решение дифференциального уравнения (10):
Решение явно неколебательное,
непериодическое.
Графики таких движений показаны на рис.6. Вид движения
зависит от начальных условий и величины коэффициента сопротивления n.
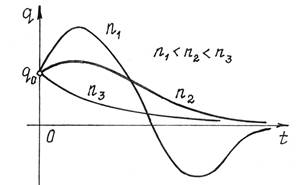
Рис.6
в) Случай
равного сопротивления (n = k).
Корни характеристического уравнения получаются равными:
. Поэтому решение дифференциального уравнения
. (14)
Движение и в этом случае не будет колебательным.
Вынужденные колебания системы.
Если сила, которая вывела систему из положения
равновесия, продолжает действовать, то такое колебание не будет свободным,
будет вынужденным. И эта сила называется возмущающей
силой.
Рассмотрим колебательное движение под действием
обобщенной возмущающей силы, изменяющейся по гармоническому закону 
, где 
- максимальная
величина возмущающей силы; р – частота изменения силы; 
– начальная фаза изменения силы.
Дифференциальное уравнение вынужденных колебаний
получится таким
(15)
Решение этого линейного неоднородного дифференциального
уравнения состоит из общего решения соответствующего однородного уравнения и
частного решения. Общее решение уже было получено в (7) или (8). Частное решение ищем в виде 
Подставив его в дифференциальное уравнение (15),
получим
Отсюда
Значит полное решение уравнения (15)
(17)
Так как общее и частное решения совершаются с разными
частотами, то вынужденные колебания не будут гармоническими. Но, как нам уже
известно, общее решение определяет свободные колебания, которые с течением
времени довольно быстро затухают. Поэтому интерес представляют только установившиеся
колебания:
Отсюда следует, что установившиеся вынужденные
колебания будут гармоническими с частотой р,
равной частоте возмущающей силы и, что они не зависят от начальных условий.
И, самое интересное, – амплитуда колебаний А
зависит от частоты р возмущающей силы. График
этой зависимости дан на рис.7.
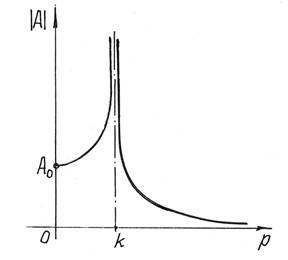
Рис.7
Первое, что надо отметить, при p = k
(частота возмущающей силы равна частоте
свободных колебаний) амплитуда увеличивается до бесконечности.
Это явление называется резонансом.
Как известно из курса высшей математики, при p = k
решение (17) не будет удовлетворять
уравнению (15). Частное решение надо искать
в другом виде:
Подставив его в уравнение (15), получим:
Отсюда 
и частное
решение, определяющее вынужденные колебания при резонансе, получится таким
Видим, что амплитуда колебаний беспредельно равномерно
увеличивается (рис.8). Амплитуда не сразу становится бесконечно большой. И даже
малая возмущающая сила может раскачать систему до больших амплитуд и вызвать
разрушение конструкции.
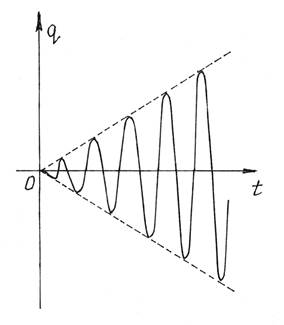
Рис.8
Интересен еще один случай, при котором частота р возмущающей силы
близка к частоте свободных колебаний, 
, но не равна
ей.
Воспользуемся
решением (17), положив для
простоты 
. Пусть в начале движения координата и скорость равнялись нулю (при t = 0 q = 0 и 
). Подставим эти начальные условия в уравнения
Получим два уравнения: 0=C1 и 0=C2k+Ap, из которых находим C1=0, C2=-Ap/k. Тогда
уравнение колебаний 
Так как 
и 
то, по (16),
Кроме того 
Уравнение
движения получится таким
(20)
Рассматривая функцию, стоящую перед cospt, как амплитуду колебаний, замечаем, что она
изменяется по гармоническому закону с периодом 
от нуля до
максимального значения 
(рис.9).
Сами колебания совершаются с частотой р и периодом 
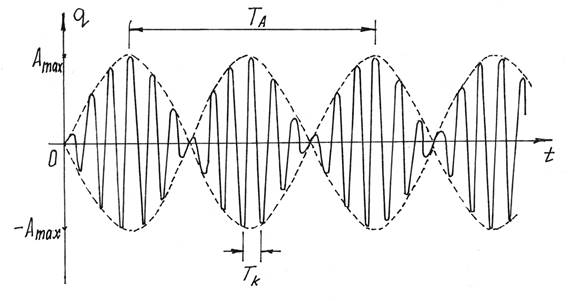
Рис.9
Чем ближе частота возмущающей силы р
к частоте k, т.е. чем ближе к резонансу,
тем больше будет период амплитуды TA и больше амплитуда Amax.
И тем больше будет похож график на рис.9 на график на
рис.8, изображающий колебания при
резонансе. Эти колебания с периодически изменяющейся амплитудой называются биениями. Такое явление часто
встречается, например, в радиотехнике.
Мы исследовали вынужденные колебания под действием
возмущающей силы, изменяющейся по гармоническому закону. Но нередко она
оказывается более сложной. Приходится использовать специальные математические
методы, чтобы получить более-менее точный результат.
Если возмущающая сила периодическая и ее можно разложить
в ряд Фурье, то решение может оказаться не очень сложным.
Пусть возмущающая сила описывается периодической
функцией Q =
Q(t) с
периодом 
, р – частота изменения этой функции. И пусть конструкция ее позволяет разложить
функцию в ряд Фурье:
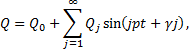
где Qj и 
- коэффициенты
Фурье, определяемые по специальным формулам.
Частное решение дифференциального уравнения (15)
получится в виде ряда:
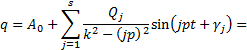
Количество s членов этого
ряда стараются иметь не очень большим, если ряд хорошо
сходится.
Решение получается как сумма нескольких синусоид
(«гармоник») с кратными частотами. Наименьшая частота р
– называется основной частотой.
Интересно, что в полученном решении возможно несколько
резонансов, столько, сколько гармоник: при p = k, p=k/2, p=k/3 и т.д.
Влияние сопротивления на вынужденные
колебания.
Если учесть сопротивление среды пропорциональное
скорости, как это было сделано выше, дифференциальное уравнение колебаний
получится таким
. (21)
Решение его состоит из общего и частного решений.
Общее мы уже находили выше. Например, при малом сопротивлении (n < k)
где 
Частное решение будем искать в виде 
. Чтобы определить коэффициенты А и 
, подставим это решение в уравнение (21). Получим
(правую часть уравнения (21)
представили как синус суммы двух углов: 
. Полученное уравнение обратится в тождество,
если будут выполнены два условия (сгруппировав члены, содержащие 
и 
:
и 
Из этих уравнений получим
Полное решение уравнения (21) будет таким
(23)
Очевидно, за счет сопротивления с течением времени
первый член стремится к нулю. Поэтому можно заключить, что установившиеся
вынужденные колебания и с учетом сопротивления среды будут гармоническими.
Причем, во-первых, частота колебаний равна частоте
изменения возмущающей силы; во-вторых, колебания не зависят от начальных
условий и, в-третьих, амплитуда колебаний А зависит от частоты р и от сопротивления среды, характеризующегося
коэффициентом n.
График этой зависимости от р
и n дан
на рис.10.
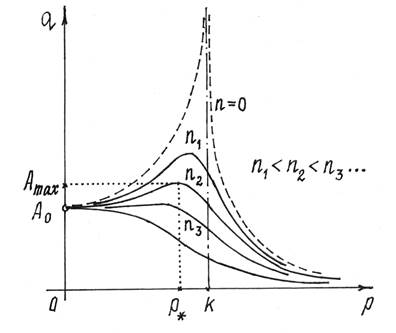
Рис.10
Из графика видно, что при сопротивлении амплитуда колебаний –
конечная величина. И максимум
амплитуды будет не при p = k, а при несколько меньшей частоте 
. Ее можно определить, отыскав максимум амплитуды А или, лучше, минимум функции F=(k2-p2)2+4n2p2
Приравняв к нулю производную, 
найдем 
И тогда
величина максимальной амплитуды, подставив в (22), 
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
