Главная

Лекция 12. Об ударе.

В данной лекции рассматриваются следующие вопросы:

1. Явление удара.

2. Прямой центральный удар двух тел.

3. Удар по вращающемуся телу.

Изучение данных вопросов необходимо для изучения колебательных движений механической системы в дисциплине «Детали машин», для решения задач в дисциплинах «Теория машин и механизмов» и «Сопротивление материалов».

Явление удара.

Ударом будем называть кратковременное действие на тело некоторой силы . Силы, возникающей, например, при встрече двух массивных тел.

Опыт показывает, что взаимодействие их очень кратковременно (время контакта исчисляется тысячными долями секунды), а сила удара довольно велика (в сотни раз превышает вес этих тел). Да и сама сила – не постоянна по величине. Поэтому явление удара - сложный процесс, сопровождающийся к тому же деформацией тел. Точное исследование его требует знания физики твердого тела, законов тепловых процессов, теории упругости и др. При рассмотрении столкновений необходимо знать форму тел, массы покоя, скорости движения и их упругие свойства.

При ударе возникают внутренние силы, значительно превышающие все внешние силы, которыми можно в этом случае пренебречь, поэтому соударяющиеся тела можно рассматривать как замкнутую систему и применять к ней законы сохранения энергии и импульса. Кроме того, эта система консервативна, т.е. внутренние силы консервативны, а внешние силы стационарны и консервативны. Полная энергия консервативной системы не изменяется со временем.

Мы же воспользуемся довольно простыми методами исследования, но которые, как подтверждает практика, достаточно правильно объясняют явление удара.

Поскольку сила удара очень велика, а продолжительность его, время , мало, при описании процесса удара будем пользоваться не дифференциальными уравнениями движения, а теоремой об изменении количества движения. Потому что измеряемой конечной величиной является не сила удара, а импульс ее

Чтобы сформулировать первые особенности явления удара, рассмотрим сначала действие такой силы на материальную точку.

Пусть к материальной точке М, движущейся под действием обычных сил по некоторой траектории (рис.1), в какой-то момент была приложена мгновенная, большая сила . С помощью теоремы об изменении количества движения за время удара составляем уравнение где и - скорости точки в конце и в начале удара; - импульс мгновенной силы . Импульсами обычных сил, под действием которых точка двигалась, можно пренебречь – за время они будут очень малы.

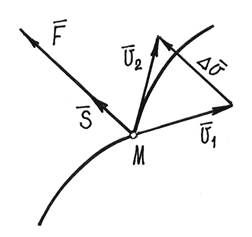
Рис.1

Из уравнения находим изменение скорости за время удара (рис.1):

.

Это изменение скорости оказывается конечной величиной.

Дальнейшее движение точки начнется со скоростью и продолжится под действием прежних сил, но по траектории, получившей излом.

Теперь можно сделать несколько выводов.

1. При исследовании явления удара обычные силы можно не учитывать.

2. Так как время мало, перемещением точки за время удара можно пренебречь.

3. Единственный результат действия удара – только изменение вектора скорости.

Прямой центральный удар двух тел.

Удар называется прямым и центральным, если центры масс тел до удара двигались по одной прямой, по оси х, точка встречи их поверхностей оказывается на этой же прямой и общая касательная Т к поверхностям будет перпендикулярна оси х (рис.2).

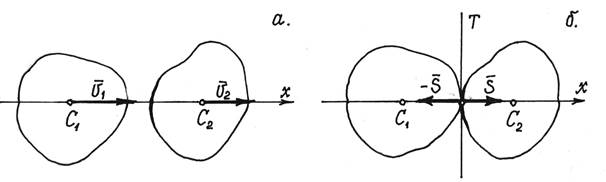
Рис.2

Если касательная Т не перпендикулярна этой оси, удар называется косым

Пусть тела двигались поступательно со скоростями их центров масс и . Определим каковы будут их скорости и после удара.

За время удара на тела действуют ударные силы , импульсы которых, приложенные в точке касания, показаны на рис.2,б. По теореме об изменении количества движения, в проекциях на ось х, получим два уравнения

где и - массы тел; - проекции скоростей на ось х.

Конечно, этих двух уравнений недостаточно для определения трех неизвестных ( и S). Нужно еще одно, которое, естественно, должно характеризовать изменение физических свойств этих тел в процессе удара, учитывать упругость материала и его диссипативные свойства.

Рассмотрим сначала удар пластичных тел, таких, которые по окончании удара не восстанавливают деформированный объем и продолжают двигаться как одно целое со скоростью u, т.е. . Это и будет недостающее третье уравнение. Тогда имеем

Решив эти уравнения, получим

Так как величина импульса S должна быть положительной, то для того чтобы произошел удар, требуется выполнение условия .

Нетрудно убедиться, что удар пластичных, неупругих тел сопровождается потерей их кинетической энергии.

Кинетическая энергия тел до удара

После удара

Отсюда

Или, учитывая (2),

И, подставив значение импульса S, по (4), получим

Эта «потерянная» энергия расходуется на деформацию тел, на нагревание их при ударе, (можно убедиться, что после нескольких ударов молотком, деформированное тело сильно нагревается).

Заметим, что если одно из тел до удара было неподвижным, например , то потерянная энергия

(так как энергия тел до удара в этом случае была только у первого тела, ). Таким образом, потеря энергии, энергии затраченной на деформацию тел, составляет часть энергии ударяющего тела.

Следовательно, при ковке металла, когда желательно чтобы было побольше, отношение нужно сделать как можно меньше, . Поэтому наковальню делают тяжелой, массивной. Аналогично, при клепке какой-либо детали, молоток надо выбирать полегче.

И, наоборот, при забивании гвоздя или сваи в грунт, молоток (или бабу копра) надо брать потяжелее, чтобы деформация тел была меньше, чтобы большая часть энергии пошла на перемещение тела.

В абсолютно неупругом ударе закон сохранения механической энергии не выполняется, но выполняется закон сохранения импульса. Потенциальная энергия шаров не меняется, меняется только кинетическая энергия – она уменьшается. Уменьшение механической энергии рассматриваемой системы обусловлено деформацией тел, которая сохраняется после удара.

Перейдем теперь к удару упругих тел.

Ударный процесс таких тел происходит гораздо сложнее. Под действием ударной силы деформация их сначала увеличивается, увеличивается до тех пор пока скорости тел не уравняются. А затем, за счет упругости материала, начнется восстановление формы. Скорости тел начнут изменяться, изменяться до тех пор пока тела не отделятся друг от друга.

Разделим процесс удара на две стадии: от начала удара до того момента, когда скорости их уравняются и будут равными u; и от этого момента до конца удара, когда тела разойдутся со скоростями и .

Для каждой стадии получим по два уравнения:

где S₁ и S₂ – величины импульсов взаимных реакций тел для первой и второй стадий.

Уравнения (6) аналогичны уравнениям (2). Решая их, получим

В уравнениях (7) три неизвестные величины (). Не хватает одного уравнения, которое опять должно характеризовать физические свойства этих тел.

Положим отношение импульсов S₂/S₁=k. Это и будет дополнительное третье уравнение.

Опыт показывает, что величину k можно считать зависящей только от упругих свойств этих тел. (Правда, более точные эксперименты показывают, что есть некоторые зависимости и от их формы). Определяется этот коэффициент экспериментально для каждых конкретных тел. Называется он коэффициентом восстановления скорости. Величина его . У пластичных тел k = 0, у абсолютно упругих тел k = 1.

Решая, теперь, уравнения (7) и (6), получим скорости тел после окончания удара.

(8)

Скорости имеют положительный знак, если они совпадают с положительным направлением оси, выбранной нами, и отрицательный – в противном случае.

Проанализируем полученные выражения для двух шаров различных масс.

1) m₁=m₂ ⇒

Шары равной массы «обмениваются» скоростями.

2) m₁>m₂, v₂=0,

u₁<v₁, следовательно, первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью;

u₂>u₁, следовательно, скорость второго шара после удара больше, чем скорость первого после удара.

3) m₁<m₂, v₂=0,

u₁<0, следовательно, направление движения первого шара при ударе изменяется – шар отскакивает обратно.

u₂<v₁, следовательно, второй шар в ту же сторону, в которую двигался первый шар до удара, но с меньшей скоростью.

4) m₂>>m₁ (например, столкновение шара со стенкой)

u₁=-v₁, , следовательно, получившее удар большое тело останется в покое, а ударившее малое тело отскочит с первоначальной скоростью в противоположную сторону.

Можно найти, как и при ударе пластичных тел, потерю кинетической энергии при ударе упругих тел. Она получится такой

Заметим, что при ударе абсолютно упругих тел (k = 1) кинетическая энергия не изменяется, не «теряется» ( T₁=T₂).

Пример 1. Металлический шарик падает с высоты h₁ на горизонтальную массивную плиту. После удара он подскакивает на высоту h₂ (рис.3).

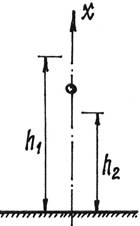
Рис.3

В начале удара о плиту проекция скорости шарика на ось х а скорость неподвижной плиты . Считая, что масса плиты , много больше массы шарика, можно положить u = 0 и u₂ = 0. Тогда по (8) . (Теперь, кстати, понятно почему коэффициент k называется коэффициентом восстановления скорости.)

Итак, скорость шарика в конце удара и направлена вверх (u₁ > 0). Шарик подскакивает на высоту h₂, связанную со скоростью формулой Значит, =k и По последней формуле, кстати, и определяется коэффициент восстановления k для материалов, из которых сделаны шарик и плита.

Пример 2. Шар массой m₁=2 кг движется со скоростью v₁=3 м/с и нагоняет шар массой m₂=8 кг, движущийся со скоростью v₂=1 м/с (рис.4). Считая удар центральным и абсолютно упругим, найти скорости u₁ и u₂ шаров после удара.

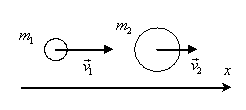
Рис.4

Решение. В случае абсолютно упругого удара выполняются законы сохранения импульса и энергии:

Отсюда следует, что

Умножив это выражение на m₂ и вычтя результат из а затем, умножив это выражение на m₁ и сложив результат с получим скорости шаров после абсолютно упругого удара

Спроецировав скорости на ось х и подставив данные задачи, получим

Знак «минус» в первом выражении означает, что в результате абсолютно упругого удара первый шар начал двигаться в обратном направлении. Второй шар продолжил движение в прежнем направлении с большей скоростью.

Пример 3. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем (рис.5). Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l= 1 м. Найти скорость v пули, если известно, что стержень с шаром отклонился от удара пули на угол α=10°.

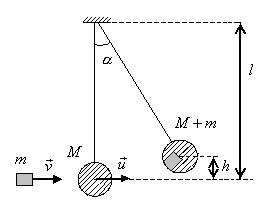
Рис.5

Решение. Для решения задачи необходимо использовать законы сохранения. Запишем закон сохранения импульса для системы «шар-пуля», полагая, что их взаимодействие подпадает под описание так называемого неупругого удара, т.е. взаимодействия, в результате которого два тела движутся как единое целое:

Учтем, что шар покоился и движение пули, а затем шара с пулей внутри происходило в одну сторону, получим уравнение в проекциях на горизонтальную ось в виде: mv=(m+M)u.

Запишем закон сохранения энергии

Поскольку h=l=lcos𝛼=l(1-cos𝛼), то , и, тогда

Учитывая, что M=1000m, получим

Пример 4. Шар массой m, двигаясь со скоростью v, упруго ударяется о стенку под углом α. Определить импульс силы F∆t, полученный стенкой.

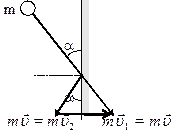
Рис.6

Решение. Изменение импульса шара численно равно импульсу силы, который получит стенка

Из рис.6 F∆t=2mv∙sinα.

Пример 5. Пуля (рис.7) веса Р₁, летящая горизонтально со скоростью u, попадает в закрепленный на неподвижной тележке ящик с песком веса Р₂. С какой скоростью будет двигаться тележка после удара, если трением колес о Землю можно пренебречь?

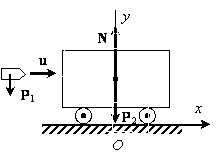
Рис.7

Решение. Будем рассматривать пулю и тележку с песком как одну систему (рис. 7). На нее действуют внешние силы: вес пули Р₁, вес тележки Р₂, а также силы реакции колес. Поскольку трение отсутствует, то эти последние направлены вертикально вверх и их можно заменить равнодействующей N. Для решения задачи воспользуемся теоремой об изменении количества движения системы в интегральной форме. В проекции на ось Ox (см. рис. 77) тогда имеем

где – количество движения системы до удара, а – после удара. Поскольку все внешние силы вертикальны, то правая часть этого уравнения равна нулю и поэтому .

Так как до удара тележка покоилась, то . После удара система движется как единое целое с искомой скоростью v и, следовательно, Q_2x=(P₁+P₂)v/g. Приравнивая эти выражения, находим искомую скорость: v=P₁u/(P₁+P₂).

Пример 6. Тело массой m₁ = 5 кг ударяется о неподвижное тело массой m₂ = 2,5 кг. Кинетическая энергия системы двух тел непосредственно после удара стала W_к = 5 Дж. Считая удар центральным и неупругим, найти кинетическую энергию W_к1 первого тела до удара.

Решение.

1) Используем закон сохранения импульса:

где v₁ - скорость первого тела до удара; v₂ - скорость второго тела до удара; v - скорость движения тел после удара.

v₂=0 т.к. по условию второе тело до удара неподвижно

2)

Т.к. удар неупругий, то скорости двух тел после удара равны, таким образом, выразив v через ω_k, получим:

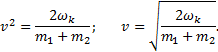
3) Отсюда имеем:

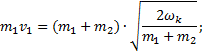
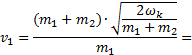
4) Подставив данное значение, найдем кинетическую энергию первого тела до удара:

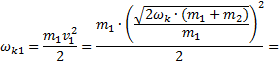
Ответ: Кинетическая энергия первого тела до удара ω_k1=7,5 Дж.

Пример 7. В конец стержня, имеющего горизонтальную ось вращения, попадает пуля массой m и застревает в нем (рис.7.1). Сохраняются ли в системе «стержень - пуля» при ударе: а) импульс; б) момент импульса относительно оси вращения стержня; в) кинетическая энергия?

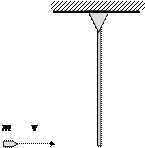
Рис.7.1

Решение. На указанную систему тел действуют внешние силы тяжести и реакции со стороны оси. Если бы ось могла перемещаться, то она после удара передвинулась бы вправо. Вследствие жесткого крепления, например, к потолку здания, импульс силы, полученный осью при взаимодействии, воспринимает вся Земля в целом. Поэтому импульс системы тел не сохраняется.

Моменты указанных внешних сил относительно оси вращения равны нулю. Следовательно, закон сохранения момента импульса выполняется.

При ударе пуля застревает вследствие действия внутренней силы трения, поэтому часть механической энергии переходит во внутреннюю (тела нагреваются). А поскольку в данном случае потенциальная энергия системы не изменяется, то уменьшение полной энергии происходит за счет кинетической.

Пример 8. На нити подвешен груз. Пуля, летящая горизонтально, попадает в груз (рис.7.2). При этом возможны три случая.

1) Пуля, пробив груз и сохранив часть скорости, летит дальше.

2) Пуля застревает в грузе.

3) Пуля после удара отскакивает от груза.

В каком из этих случаев груз отклонится на наибольший угол α?

Рис.7.2

Решение. При ударе материальных точек выполняется закон сохранения импульса. Обозначим скорость пули до удара через v, массы пули и груза через m₁ и m₂ соответственно, скорости пули и груза после удара - u₁ и u₂. Совместим координатную ось х с вектором скорости пули.

В первом случае закон сохранения импульса в проекции на ось х имеет вид:

причем, u₂>u₁.

Во втором случае закон сохранения импульса имеет тот же вид, но скорости тел после удара совпадают u₂=u₁=u:

В третьем случае закон сохранения импульса принимает следующий вид:

Из выражений (1) - (3) выразим импульс груза после удара:

Видно, что в третьем случае импульс груза наибольший, следовательно и угол отклонения принимает максимальное значение.

Пример 9. Материальная точка массы m упруго ударяется о стенку (рис.7.3). Изменяется ли при ударе момент импульса точки:

1) относительно точки А;

2) относительно точки В?

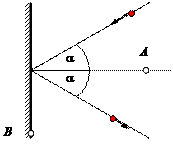
Рис.7.3

Решение. Эту задачу можно решить двумя способами:

1) используя определение момента импульса материальной точки,

2) на основе закона изменения момента импульса.

Первый способ.

По определению момента импульса имеем:

где r - радиус-вектор, определяющий положение материальной точки, p=mv - ее импульс.

Модуль момента импульса рассчитывается по формуле:

где α - угол между векторами r и р.

При абсолютно упругом ударе о неподвижную стенку модуль скорости материальной точки и, следовательно, модуль импульса не изменяются p_I=p_II=p, кроме того, угол отражения равен углу падения.

Модуль момента импульса относительно точки А (рис.7.4) равен до удара

после удара

Направления векторов L_I и L_II можно определить по правилу векторного произведения; оба вектора направлены перпендикулярно плоскости рисунка “к нам”.

Следовательно, при ударе момент импульса относительно точки А не изменяется ни по величине, ни по направлению.

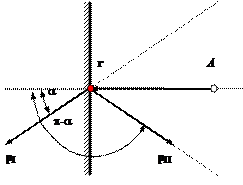
Рис.7.4

Модуль момента импульса относительно точки В (рис.7.5) равен как до, так и после удара

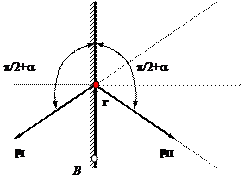
Рис.7.5

Ориентации векторов L_I и L_II в данном случае будут различны: вектор L_I по-прежнему направлен “к нам”, а вектор

L_II - “от нас”. Следовательно, момент импульса относительно точки В претерпевает изменение.

Второй способ.

Согласно закону изменения момента импульса имеем:

где M=[r,F] - момент силы взаимодействия материальной точки со стенкой, его модуль равен M=Frsinα. Во время удара на материальную точку действует упругая сила, возникающая при деформации стенки и направленная по нормали к ее поверхности (сила нормального давления N). Силой тяжести в данном случае можно пренебречь, за время удара она практически не оказывает влияния на характеристики движения.

Рассмотрим точку А. Из рис.7.6 видно, что угол между вектором силы N и радиус-вектором , проведенным от точки А к взаимодействующей частице, α=π, sinα=0. Следовательно, М = 0 и L_I=L_II. Для точки В α=π/2, sinα=1. Следовательно, и момент импульса относительно точки В изменяется.

Рис.7.6

Пример 10. Молекула массой m, летящая со скоростью v, ударяется о стенку сосуда под углом α к нормали и упруго отскакивает от нее (рис.7.7). Найти импульс, полученный стенкой за время удара.

Рис.7.7

Решение. При абсолютно упругом ударе выполняется закон сохранения энергии. Поскольку стенка неподвижна, кинетическая энергия молекулы, а следовательно и модуль скорости не изменяется. Кроме того, угол отражения молекулы равен углу, под которым она движется к стенке.

Изменение импульса молекулы равно импульсу силы, полученному молекулой от стенки:

p_II-p_I=F∆t,

где F - средняя сила, с которой стенка действует на молекулу, p_I=mv, p_II=mv - импульсы молекулы до и после удара.

Спроектируем векторное уравнение на оси координат:

Σx=0: mv∙cosα-(-mv∙cosα)=F_x∆t,

Σy=0: mv∙sinα-mv∙sinα=F_y∆t, F_y=0.

откуда величина импульса силы, полученного молекулой, равна

F∆t=F_x∆t=2mv∙cosα.

По третьему закону Ньютона величина силы, с которой стенка действует на молекулу равна силе, действующей со стороны молекулы на стенку. Поэтому стенка получает точно такой же импульс F∆t=2mv∙cosα, но направленный в противоположную сторону.

Пример 11. Боек свайного молота массой m₁ падает с некоторой высоты на сваю массой m₂. Найти КПД удара бойка, считая удар неупругим. Изменением потенциальной энергии сваи при ее углублении пренебречь.

Решение. Рассмотрим систему тел, состоящую из бойка молота и сваи. До удара (состояние I) боек движется со скоростью v₁, свая неподвижна. Суммарный импульс системы p_I=m₁v₁, ее кинетическая энергия (затраченная энергия)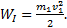

После удара оба тела системы движутся с одинаковой скоростью u. Их суммарный импульс p_II=(m₁+m₂)u, а кинетическая энергия (полезная энергия)

По закону сохранения импульса p_I=p_II имеем

откуда выражаем конечную скорость

Коэффициент полезного действия равен отношению полезной энергии к затраченной, т.е.

Следовательно,

С помощью выражения (1) окончательно получаем:

Удар по вращающемуся телу.

При исследовании удара по вращающемуся телу кроме теоремы об изменении количества движения приходится использовать и закон моментов. Относительно оси вращения его запишем так и, после интегрирования за время удара , или где и - угловые скорости тела в начале и в конце удара, - ударные силы.

Правую часть надо немного преобразовать. Найдем, сначала, интеграл момента ударной силы относительно неподвижной точки О:

При этом предполагалось, что за малое время удара τ радиус-вектор считался неизменным, постоянным.

Проектируя результат этого векторного равенства на ось вращения z, проходящую через точку О, получим , т.е. интеграл равен моменту вектора импульса ударной силы относительно оси вращения. Закон моментов в преобразованном виде запишется, теперь, так:

. (10)

В качестве примера рассмотрим удар вращающегося тела о неподвижную преграду.

Тело, вращаясь вокруг горизонтальной оси О, ударяется о преграду А (рис.8). Определим ударные импульсы сил, возникающих в подшипниках на оси, и .

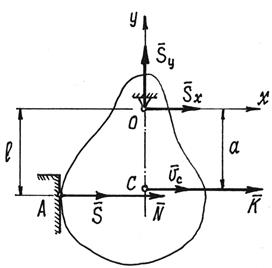
Рис.8

По теореме об изменении количества движения в проекциях на оси х и у получим два уравнения:

где скорости центра масс С в начале и конце удара Поэтому первое уравнение станет таким .

Третье уравнение, по (10), получится в виде из которого находим .

И, так как коэффициент восстановления

то (в нашем примере , поэтому ударный импульс S > 0, то есть направлен так, как показано на рисунке).

Находим импульсы реакции оси:

Обязательно надо обратить внимание на то, что при ударные импульсы в подшипниках оси будут равны нулю.

Место, точка удара, расположенная на этом расстоянии от оси вращения, называется центром удара. При ударе по телу в этом месте ударные силы в подшипниках не возникают.

Кстати, заметим, что центр удара совпадает с точкой где приложены равнодействующая сил инерции и вектор количества движения.

Вспомним, что при ударе длинной палкой по неподвижному предмету, мы нередко испытывали рукой неприятный ударный импульс, как говорят – «отбивали руку».

Нетрудно найти в этом случае центр удара – место, которым следует ударить, чтобы не почувствовать это неприятное ощущение (рис.9).

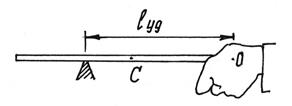
Рис.9

Так как (l – длина палки) и a=OC=0,5l то

Следовательно, центр удара находится на расстоянии трети длины от конца палки.

Понятие центра удара учитывают при создании различных ударных механизмов и других конструкций, где встречаются ударные процессы.

Пример 12. Стержень массы m₂ и длины l, который может свободно вращаться вокруг неподвижной горизонтальной оси, проходящей через один из его концов, под действием силы тяжести переходит из горизонтального положения в вертикальное. Проходя через вертикальное положение, нижний конец стержня ударяет о небольшой кубик массы m₁, лежащий на горизонтальном столе. Определить:

а) на какое расстояние переместится кубик m₁, если коэффициент трения о поверхность стола равен μ;

б) на какой угол отклонится стержень после удара.

Рассмотреть случаи абсолютно упругого и неупругого ударов.

Рис.10

Решение. В задаче описывается несколько процессов: падение стержня, удар, движение кубика, подъем стержня. Рассмотрим каждый из процессов.

Падение стержня. На стержень действует потенциальная сила тяжести и сила реакции оси, которая работы при вращательном движении стержня не совершает, т.к. момент этой силы равен нулю. Следовательно, выполняется закон сохранения энергии.

В начальном горизонтальном состоянии стержень обладал потенциальной энергией

где h - высота подъема центра масс стержня H=l/2,

В конечном вертикальном состоянии (до удара) стержень обладал кинетической энергией вращательного движения

где J - момент инерции стержня относительно оси, проходящей через его конец:

ω - угловая скорость. Следовательно,

По закону сохранения энергии W_I=W_II получаем:

откуда угловая скорость стержня до удара равна

Процесс удара. Система состоит из двух тел - стержня и кубика. Рассмотрим случаи неупругого и упругого ударов.

Неупругий удар. При ударе материальных точек или твердых тел, движущихся поступательно, выполняется закон сохранения импульса. Если хотя бы одно из взаимодействующих тел совершает вращательное движение, то следует применять закон сохранения момента импульса. При неупругом ударе оба тела после удара начинают движение с одной и той же угловой скоростью, скорость кубика совпадает с линейной скоростью нижнего конца стержня.

До удара (состояние II) двигался только стержень, его момент импульса относительно оси, проходящей через точку подвеса, равен:

После удара (состояние III) движутся стержень и кубик с одинаковой угловой скоростью ω₃. Их момент импульса равен

Здесь - момент инерции кубика (материальной точки) относительно рассматриваемой оси.

По закону сохранения момента импульса L_II=L_III имеем

Откуда

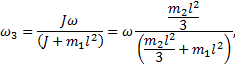
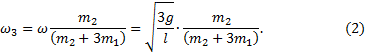
Линейная скорость кубика равна

Упругий удар. После абсолютно упруго удара оба тела движутся по отдельности. Кубик движется со скоростью v, стержень - с угловой скоростью ω₃. Кроме закона сохранения момента импульса для этой системы тел выполняется закон сохранения энергии.

До удара (состояние II) двигался только стержень, его момент импульса относительно оси, проходящей через точку подвеса, равен

а кинетическая энергия определяется выражением

После удара (состояние III) момент импульса стержня , момент импульса кубика (материальной точки , поэтому суммарный момент импульса системы

Кинетическая энергия вращательного движения стержня составит , а кинетическая энергия кубика , поэтому полная энергия системы равна

Применим законы сохранения энергии W_II=W_III и момента импульса L_II=L_III:

Получили систему двух уравнений с двумя неизвестными. Преобразуем ее к виду:

Разделим (6) на (7) и учтем, что

Подставляя в уравнение (7)

получим выражение для угловой скорости стержня.

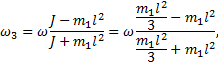
Скорость кубика

Подъем стержня (рис.11). Этот процесс, также как и первый, описывается законом сохранения энергии.

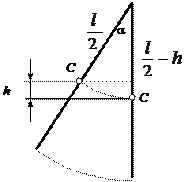
Рис.11

Кинетическая энергия стержня превращается в его потенциальную энергию , то есть

откуда высота подъема центра масс стержня

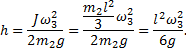
Определим угол отклонения стержня. Проведем расчет только для неупругого удара. Из рисунка видно, что

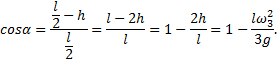
Подставим формулу (2) в последнее выражение:

Движение кубика. В процессе движения на кубик действуют сила тяжести m₁g, сила нормального давления N и сила трения скольжения Кинетическая энергия кубика уменьшается до нуля вследствие того, что сила трения совершает работу. Следовательно, по теореме о кинетической энергии

откуда перемещение кубика составит

где скорость при неупругом ударе определяется выражением (3).

Вопросы для самопроверки

- Какое явление называется ударом?

- Чем характеризуется ударная сила?

- Какой эффект имеет действие ударной силы на материальную точку?

- Охарактеризуйте действие ударной силы на материальную точку.

- Сформулируйте теорему об изменении количества движения механической системы при ударе в векторной форме и в проекциях на оси координат.

- Могут ли внутренние ударные импульсы изменить количество движения механической системы?

- Что называют коэффициентом восстановления при ударе и как он определяется опытным путем? В каких пределах находятся его числовые значения?

- Какова зависимость между углами падения и отражения при ударе о гладкую неподвижную поверхность?

- Чем характеризуются первая и вторая фазы упругого удара? В чем состоит особенность абсолютно упругого удара?

- Как определяются скорости двух шаров в конце каждой фазы прямого центрального удара (неупругого, упругого, абсолютно упругого)?

- Какова зависимость между ударными импульсами второй и первой фаз при абсолютно упругом ударе?

- Какова потеря кинетической энергии двух соударяющихся тел при неупругом, упругом и абсолютно упругом ударах?

- Как формулируется теорема Карно?

- Как формулируется теорема об изменении кинетического момента механической системы при ударе в векторной форме и в проекциях на оси координат?

- Могут ли внутренние ударные импульсы изменить кинетический момент механической системы?

- Какие изменения вносит действие ударных сил в движение твердых тел: вращающегося вокруг неподвижной оси и совершающего плоское движение?

- При каких условиях опоры вращающегося тела не испытывают действия внешнего ударного импульса, приложенного к телу?

- Что называют центром удара и каковы его координаты?

Задачи для самостоятельного решения

Задача 1. Снаряд массой 100 кг летящий горизонтально вдоль железнодорожного пути со скоростью 500 м/с, попадает в вагон с песком массой 10 т и застревает в нем. Какую скорость получит вагон, если: 1) вагон стоял неподвижно, 2) вагон двигался со скоростью 36 км/ч в том же направлении, что и снаряд, 3) вагон двигался со скоростью 36 км/ч в направлении, противоположном движению снаряда?

Задача 2. Тело массой 2 кг движется со скоростью 3 м/с и нагоняет второе тело массой 3 кг, движущееся со скоростью 1 м/с. Найти скорости тел после столкновения, если: 1) удар был неупругий, 2) удар был упругий. Тела движутся по одной прямой. Удар - центральный.

Задача 3. Пуля массой 10 г, летевшая со скоростью 400 м/с, пробив доску толщиной 5 см, уменьшила скорость вдвое. Определить силу сопротивления доски движению пули.

Задача 4. Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шара 0,2 кг, масса второго 100 г. Первый шар отклоняют так, что его центр тяжести поднимается на высоту 4,5 см, и отпускают. На какую высоту поднимутся шары после соударения, если: 1) удар упругий, 2) удар неупругий?

Задача 5. Пуля, летящая горизонтально, попадает в шар, подвешенный на очень легком жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от точки подвеса стержня до центра шара равно 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара пули на угол 10°.

Задача 6. Молот массой 1,5 т ударяет по раскаленной болванке, лежащей на наковальне и деформирует болванку. Масса наковальни вместе с болванкой равна 20 т. Определить КПД при ударе молота, считая удар неупругим. Считать работу, совершенную при деформации болванки, полезной.

Задача 7. Молот массой m₁ = 5 кг ударяет небольшой кусок железа, лежащий на наковальне. Масса наковальни m₂ = 100 кг. Массой куска железа пренебречь. Удар неупругий. Определить КПД удара молота при данных условиях.

Задача 8. Тело массой 2 кг движется со скоростью 3 м/с и нагоняет второе тело массой 3 кг, движущееся со скоростью 1 м/с. Найти скорости тел после столкновения, если: 1) удар был неупругий, 2) удар был упругий. Тела движутся по одной прямой. Удар - центральный.

Задача 9. Пуля массой 10 г, летевшая горизонтально, попадает в подвешенный шар массой 2 кг, и, пробив его, вылетает со скоростью 400 м/с, причем шар поднимается на высоту 0,2 м. Определить: а) с какой скоростью летела пуля; б) какая часть кинетической энергии пули при ударе перешла во внутреннюю.

Задача 10. Деревянный шар массой М лежит на штативе, верхняя часть которого выполнена в виде кольца. Снизу в шар попадает пуля, летящая вертикально, и пробивает его. При этом шар поднимается на высоту h. На какую высоту поднимется пуля над штативом, если ее скорость перед ударом о шар была v ? Масса пули m.

Задача 11. В ящик с песком массой M=5 кг, подвешенный на длинной нити l=3 м, попадает пуля массой m=0,05 кг и отклоняет его на угол α=10°. Определить скорость пули.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00