Главная

Лекция 7. Приложение общих теорем к динамике твердого тела.

В данной лекции рассматриваются следующие вопросы:

1. Неинерциальные системы отсчета.

2. Силы инерции при поступательном движении.

3. Центробежная сила инерции.

4. Сила Кориолиса.

5. Принцип Даламбера.

6. Главный вектор и главный момент сил инерции твердого тела.

7. Вращательное движение твердого тела.

8. Физический маятник.

9. Плоскопараллельное движение твердого тела.

10. Сложное движение твердого тела и системы тел.

11. Движение тела с переменной массой.

12. Совместное применение законов динамики и методов решения кинематических задач.

13. Совместное применение законов динамики и законов сохранения. Выбор способа решения.

14. Решение задач различными способами.

15. Применение неинерциальной системы отсчета.

16. Решение нестандартных задач.

17. Решение многоходовых задач.

Изучение данных вопросов необходимо для изучения демпферов в дисциплине «Детали машин», для решения задач в дисциплинах «Теория машин и механизмов» и «Сопротивление материалов».

Неинерциальные системы отсчета.

До сих пор движение тела рассматривалось по отношению к какой-либо одной из бесчисленного множества инерциальных систем отсчета. В такой системе отсчета основным уравнением движения тела является уравнение, выражающее второй закон Ньютона:

Законы Ньютона выполняются только в инерциальных системах отсчета. Относительно всех инерциальных систем данное тело движется с одинаковым ускорением . Поставим теперь задачу найти уравнение движения в неинерциальных системах отсчета, т.е. таких системах, в которых первый закон Ньютона не выполняется.

Любая неинерциальная система отсчета движется относительно инерциальных систем с некоторым ускорением, поэтому ускорение тела в неинерциальной системе отсчета будет отлично от .

Обозначим разность ускорения тела в инерциальной и неинерциальной системах символом :

В частном случае, когда неинерциальная система отсчета движется относительно инерциальной поступательно, ускорение тела одинаково для всех точек пространства (=const) и представляет собой ускорение неинерциальной системы отсчета.

Систему отсчета, связанную с Землей, приближенно можно считать инерциальной при решении большинства задач.

Силы инерции при поступательном движении.

Ускорение точки в неинерциальной системе отсчета можно в соответствии с (2) представить в виде:

Подставим выражение (3) в уравнение (1) и получим:

Это и есть уравнение движения материальной точки относительно неинерциальной системы отсчета. Если в неинерциальной системе отсчета определять силу как вектор, равный произведению массы материальной точки на ее ускорение в этой системе отсчета, то правая часть уравнения (6.4) и является силой, действующей на материальную точку, движущуюся ускоренно в неинерциальной системе отсчета. Эта сила слагается из двух существенно различных составляющих. Первая оставляющая является результатом взаимодействия тел и проявляется в инерциальной системе отсчета.

Совсем иной характер имеет составляющая – . Она возникает не из-за взаимодействия тел, а из-за ускоренного движения системы отсчета. Она называется поступательной силой инерции. При переходе к другой ускоренно движущейся системе отсчета меняются и силы инерции. Эти силы инерции отличаются от настоящих сил, возникающих при взаимодействии тел. Второе отличие состоит в том, что силы инерции не подчиняются закону действия и противодействия (третьему закону Ньютона).

При описании движения тел относительно ускоренно движущейся поступательно системы отсчета наряду с силами, обусловленными взаимодействием тел друг с другом, необходимо учитывать так называемые силы инерции . Эти силы следует полагать равными произведению массы тела на взятое с обратным знаком ускорение движущейся неинерциальной системы отсчета относительно инерциальной системы:

Соответственно, уравнение движения в неинерциальной системе отсчета будет иметь вид

Существует много явлений, которые могут быть интерпретированы как проявление силы инерции. Когда поезд набирает скорость, пассажиры в вагоне испытывают действие силы, направленной против движения поезда. Это и есть сила инерции. Силы инерции вызывают перегрузки, действующие на летчика при больших ускорениях самолета. Если в ускоренно движущемся вагоне висит шарик массы m, то сила инерции отклоняет его в сторону, противоположную ускорению (рис.1).

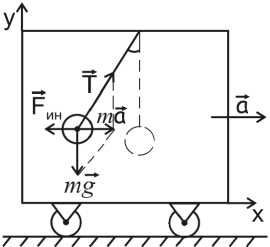
Рис.1

Нить отклоняется на такой угол, чтобы результирующая двух сил () сообщала шарику ускорение , с которым движется вагон. Относительно системы отсчета, связанной с вагоном, шарик покоится. Это можно объяснить, если ввести силу инерции , уравновешивающую результирующую двух сил и .

Введение сил инерции дает возможность описывать движение тел в любых системах отсчета с помощью одних и тех же уравнений движения.

Силы инерции имеют характерные особенности: они не отражают взаимодействие тел, а обусловлены характером неинерциальных систем отсчета, поэтому для сил инерции неприменим третий закон Ньютона. Характерным свойством сил инерции является их пропорциональность массе тела. Благодаря этому свойству силы инерции оказываются аналогичными силам тяготения. Движение тел под действием сил инерции сходно с движением в гравитационном поле. В качестве примера можно привести невесомость, возникающую в свободно падающем лифте. В свободно падающем лифте вес тела массой m всегда равен нулю: .

Действительно:

Рассмотрим силы инерции, возникающие во вращающихся системах отсчета.

Центробежная сила инерции.

Рассмотрим два случая проявления центробежной силы инерции.

Случай 1. Рассмотрим вращающийся диск с закрепленными на нем стойками с шариками, подвешенными на нитях (рис.2). При вращении диска с постоянной угловой скоростью w шарики отклоняются на некоторый угол, тем больший, чем дальше он находится от оси вращения. Относительно инерциальной системы отсчета (неподвижной) все шарики движутся по окружности соответствующего радиуса R, при этом на шарики действует результирующая сила (рис.3).

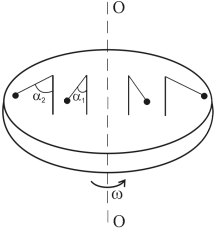
Рис.2

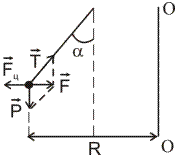
Рис.3

Согласно второму закону Ньютона

учитывая, что F/P=tgα, можно записать

т.е. угол отклонения шарика зависит от угловой скорости и от его удаления от оси вращения диска.

Относительно неинерциальной системы отсчета, связанной с вращающимся диском, шарик находится в покое.

Это возможно в том случае, если сила (8) уравновешена силой инерции , называемой центробежной силой инерции:

Случай 2. Рассмотрим диск, вращающийся вокруг перпендикулярной к нему вертикальной оси z с угловой скоростью ω. Вместе с диском вращается надетый на тонкую спицу шарик, соединенный с центром диска пружиной (рис. 4).

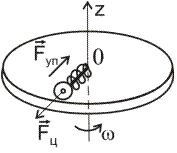
Рис.4

Шарик занимает на стержне некоторое положение, при котором сила натяжения пружины (она будет центростремительной) оказывается равной произведению массы шарика m на его ускорение:

где – нормальное ускорение на шарике; r – расстояние от оси вращения до центра шарика.

Относительно системы отсчета, связанной с диском, шарик покоится. Это формально можно объяснить тем, что кроме силы упругости на шарик действует сила инерции, модуль которой равен силе упругости (7):

Сила инерции направлена вдоль радиуса от центра диска. Силу инерции (8), возникающую в равномерно вращающейся системе отсчета, называют центробежной силой инерции. Эта сила действует на тело во вращающейся системе отсчета, независимо от того, покоится тело в этой системе или движется относительно нее со скоростью . Если положение тела во вращающейся системе отсчета характеризовать радиус-вектором , то центробежную силу можно представить в виде

где – компонента радиус-вектора, направленная перпендикулярно оси вращения.

Центробежные силы, как и всякие силы инерции, существуют только в ускоренно движущихся (вращающихся) системах отсчета и исчезают при переходе к инерциальным системам отсчета.

Действию центробежной силы подвергается, например, пассажир в движущемся автобусе на поворотах. Если в центробежной машине подвесить на нитях несколько шариков и привести машину в быстрое вращение, то центробежные силы инерции отклонят шарики от оси вращения. Угол отклонения тем больше, чем дальше шарик отстоит от оси. Центробежные силы используются в центробежных сушилках для отжима белья, в сепараторах для отделения сливок от молока, в центробежных насосах, центробежных регуляторах и т.д. Их надо учитывать при проектировании быстровращающихся деталей механизмов.

Сила Кориолиса.

При движении тела относительно вращающейся системы отсчета, кроме центробежной силы, появляется еще одна сила, называемая силой Кориолиса.

Рассмотрим рис.5. Шарик массой m движется прямолинейно со скоростью от центра к краю диска. Если диск неподвижен, то шарик попадает в точку М, а если диск вращается с постоянной угловой скоростью ω, то шарик попадает в точку N. Это обусловлено тем, что на шарик действует сила Кориолиса.

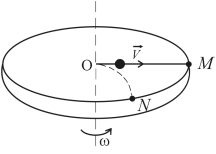
Рис.5

Появление силы Кориолиса можно обнаружить, если рассмотреть пример с шариком на спице на вращающемся диске, но без пружины. Для того чтобы заставить шарик двигаться с некоторой скоростью вдоль спицы, необходима боковая сила. Шарик вращается вместе с диском с постоянной угловой скоростью w, поэтому его момент импульса равен:

Если шарик будет перемещаться вдоль спицы с постоянной скоростью , то с изменением момент импульса шарика изменится. А это означает, что на движущееся во вращающейся системе тело должен действовать некоторый момент силы, который согласно основному уравнению динамики вращательного движения равен

Для того чтобы заставить шарик двигаться по вращающемуся диску вдоль радиальной прямой со скоростью , необходимо прилагать боковую силу

направленную перпендикулярно . Относительно вращающейся системы (диска) шарик движется с постоянной скоростью.

Это можно объяснить тем, что сила уравновешивается приложенной к шарику силой инерции , перпендикулярной к скорости (рис.6). Сила и есть Кориолисова сила инерции. Она определяется выражением

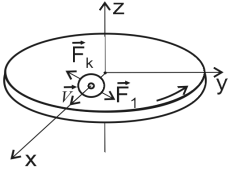
Рис.6

С учетом направления силу Кориолиса можно представить в виде

Сила Кориолиса всегда перпендикулярна скорости тела . Во вращающейся системе отсчета при = 0 эта сила отсутствует. Таким образом, Кориолисова сила инерции возникает только тогда, когда система отсчета вращается, а тело движется относительно этой системы. Действием силы Кориолиса объясняется ряд эффектов, наблюдающихся на поверхности Земли, например, поворот плоскости колебаний маятника Фуко относительно Земли, отклонение к востоку от линии отвеса свободно падающих тел, размытие правого берега рек в северном полушарии и левого в южном, неодинаковый износ рельсов при двухколейном движении.

Принцип Даламбера.

Все методы решения задач динамики, которые мы до сих пор рассматривали, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являющихся следствиями этих законов. Однако, этот путь не является единственным. Оказывается, что уравнения движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Даламбера.

Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой . Под действием приложенных к ней внешних и внутренних сил и (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение .

Введем в рассмотрение величину

,

имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки (иногда даламберовой силой инерции).

Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам и прибавить силу инерции , то полученная система сил будет уравновешенной, т.е. будет

.

Это выражение выражает принцип Даламбера для одной материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает . Перенося здесь член в правую часть равенства и придем к последнему соотношению.

Повторяя проделанные высшее рассуждения по отношению к каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики.

Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Кроме того, в соединении с принципом возможных перемещений, который будет рассмотрен в следующей главе, принцип Даламбера позволяет получить новый общий метод решения задач динамики.

Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы и , возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями . Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции - это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики.

Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систе6му. Тогда на основании принципа Даламбера должно быть:

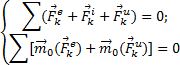
Введём обозначения:

Величины и представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:

Применение уравнений (16), вытекающих из принципа Даламбера, упрощает процесс решения задач, т.к. эти уравнения не содержат внутренних сил.

В проекциях на оси координат эти равенства дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, надо знать выражение главного вектора и главного момента сил инерций.

Пример 1. При каком минимальном значении скорости тяжелый шарик пройдет высшую точку петли радиуса R, не отрываясь от нее (рис.6.1)? Петля расположена в вертикальной плоскости.

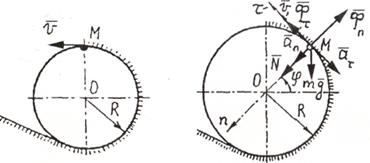
Рис.6.1

Решение. Будем считать шарик материальной точкой в промежуточном положении на его траектории. Приложим к шарику силу тяжести mg, нормальную реакцию петли , касательную и нормальную силы инерции , .

Согласно принципу Даламбера для точки получим уравновешенную в любой момент времени систему сил

Проектируя эту систему сил на главную нормаль Mn получим

где Ф_n = ma_n, а_n = v²/R - нормальное ускорение шарика, (v— скорость шарика).

По условию задачи при ψ= 90° нормальная реакция в верхней точке петли N= 0, то есть

Отсюда

Скорость шарика

Пример 2. Однородный стержень АВ длиной l и массой т, закрепленный шарнирно на валу OO₁ вращается вокруг оси Оу с постоянной угловой скоростью ω (рис.6.2). Стержень удерживается под углом α к вертикали при помощи горизонтальной тяги BD. Найти реакции шарниров А и В.

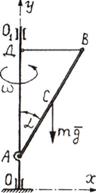
Рис.6.2

Решение. Применим для решения задачи принцип Даламбера. Приложим к стержню силу тяжести mg, составляющие реакции и шарнира А вдоль осей координат, реакцию шарнира В (рис.6.3).

Силы инерции точек стержня заменим равнодействующей нормальной силой инерции , приложенной в точке К, причем

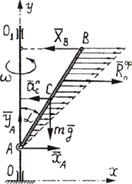
Рис.6.3

Получена уравновешенная в любой момент времени система сил

где - нормальное ускорение центра масс стержня (точки С); АС= СВ.

Условия мгновенного динамического равновесия стержня имеют вид

Из составленной системы уравнений с учетом значения силы последовательно находим

Пример 3. Однородный гладкий диск массы m и радиуса r установлен между валом OO₁ и стержнем АВ, прикрепленным к нему под углом ѱ. Стержень и вал вращаются с постоянной угловой скоростью w вокруг оси Оу (рис.6.4). Определить давление диска на стержень и вал.

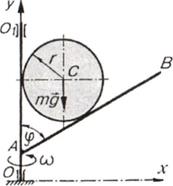
Рис.6.4

Решение. Воспользуемся принципом Даламбера.

Приложим к диску силу тяжести mg, реакцию вала и реакцию стержня , а также равнодействующую нормальную силу инерции всех точек диска, причем

где - нормальное ускорение центра масс диска (точки С).

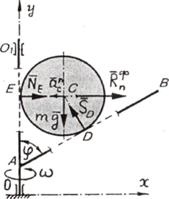
Рис.6.5

Сходящаяся система сил (mg, , , ) является уравновешенной в любой момент времени.

Составим уравнения мгновенного динамического равновесия диска (указанной выше сходящихся системы сил)

Из этой системы уравнений с учетом значения силы находим:

Давление диска на стержень и вал в точках В и D равны соответствующим реакциям стержня и вала

Q_D = S_D; Р_Е = N_Е.

Главный вектор и главный момент сил инерции твёрдого тела.

Система сил инерции твёрдого тела можно заменить одной силой, равной и приложенной в центре О, и парой с моментом, равным . Главный вектор системы сил, как известно, не зависит от центра приведения и может быть вычислен заранее. Т.к. , то

Следовательно, главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.

Прикладывается главный вектор к точке приведения, которую можно назначить в любом месте, т.е. он не зависит от выбора этой точки.

Если ускорение разложить на касательное и нормальное, то вектор разложиться на составляющие

С определением главного момента сил инерции возникает немало сложностей. Рассмотрим несколько частных случаев.

1. Поступательное движение. В этом случае тело никакого вращения вокруг центра масс С не имеет. Отсюда заключаем, что , и равенство (1) даёт .

Следовательно, при поступательном движении силы инерции твёрдого тела приводят к одной равнодействующей, равной и проходящей через центр масс тела.

2. Плоскопараллельное движение. Пусть тело имеет плоскость симметрии и движется параллельно ей. Вследствие симметрии главный вектор и результирующая пара сил инерции, так же как и центр масс С тела, лежат в плоскости симметрии.

Тогда, помещая центр приведения в точке С, получим из равенства (16) . С другой стороны . Отсюда заключаем, что

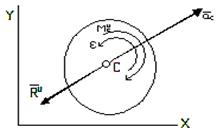
Рис.7

Таким образом, в рассмотренном случае движение системы сил инерции приводится к результирующей силе, равной [формула (18)] и приложенной в центре масс С тела (рис.7), и к лежащей в плоскости симметрии тела паре, момент которой определяется формулой (18). Знак минус в формуле показывает, что направление момента противоположно направлению углового ускорения тела.

3. Вращение вокруг оси, проходящей через центр масс тела. Пусть опять тело имеет плоскость симметрии, а ось вращения СZ перпендикулярна к этой плоскости и проходит через центр масс тела. Тогда данный случай будет частным случаем предыдущего. Но при этом а следовательно, и .

Таким образом, в рассмотренном случае система сил инерции приводится к данной паре, лежащей в плоскости, перпендикулярной к оси вращения тела, и имеющей момент

.

При решение задач по формулам (16) и (18) вычисляются модули соответствующих величин, а направление их указывают на чертеже.

Приложение общих теорем к динамике твердого тела.

Вращательное движение твёрдого тела.

Рассмотрим приложения общих теорем динамики к некоторым задачам о движении абсолютно твёрдого тела. Так как изучение поступательного движения твёрдого тела сводится к задачам динамики точки, то мы начнём непосредственно с рассмотрения вращательного движения.

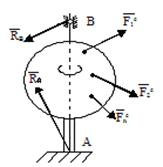
Рис.8

Пусть на твёрдое тело, имеющее неподвижную ось вращения Z (рис.8), действует система заданных сил . Одновременно на тело действуют реакции подшипников и . Чтобы исключить из уравнения движения эти наперед неизвестные силы, воспользуемся теоремой моментов относительно оси Z. Так как моменты сил и относительно оси Z равны нулю, то получим:

Будем в дальнейшем величину называть вращающим моментом.

Подставляя в предыдущее равенство значение , найдём:

Уравнение представляет собой дифференциальное уравнение вращательного движения твёрдого тела. Из него следует, что произведение момента инерции тела относительно оси вращения на угловое ускорение равно вращающему моменту:

Равенство показывает, что при данном чем больше момент инерции тела, тем меньше угловое ускорение и наоборот. Следовательно, момент инерции тела действительно играет при вращательном движении такую же роль, как масса при поступательном, т.е. является мерой инертности тела при вращательном движении.

Отметим следующие частные случаи:

1) Если , то , т.е. тело вращается равномерно.

2) Если , то и , т.е. тело вращается равнопеременно.

Пример 3. Стержень весом Р и длиной l качается как маятник в вертикальной плоскости, вращаясь вокруг горизонтальной оси О (рис.9).

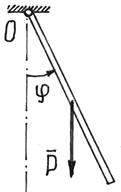
Рис.9

Решение. Составим уравнение качаний стержня.

Так как и реакции оси не учитываются, то получим

Физический маятник

Физическим маятником называется твёрдое тело, которое может совершать колебания вокруг неподвижной горизонтальной оси под действием силы тяжести.

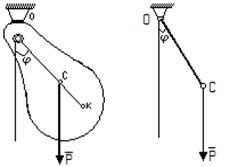
а) б)

Рис.10

Изобразим сечение маятника плоскостью, перпендикулярной оси подвеса и проходящей через центр масс маятника С (рис.10, а).

Введём обозначения: Р – вес маятника, а – расстояние ОС от центра масс до оси подвеса, I₀ – момент инерции маятника относительно оси подвеса. Положения маятника будет определять угол отклонение линии ОС от вертикали.

Для определения закона колебаний маятника воспользуемся дифференциальным уравнением вращательного движения. В данном случае (знак минус взят потому, что при момент отрицателен, а при – положителен) и уравнение принимает вид:

Деля обе части равенства на I₀ и вводя обозначение

найдём дифференциальное уравнение колебаний маятника в виде

Полученное дифференциальное уравнение в обычных функциях не интегрируется. Ограничимся рассмотрением малых колебаний маятника, считая приближенно (это можно сделать, когда угол меньше одного радиана). Тогда будем иметь

Это дифференциальное уравнение совпадает по виду с дифференциальным уравнением свободных прямолинейных колебаний точки, и его общее решение по аналогии имеет вид:

Полагая, что начальный момент t = 0 маятник отклонён на малый угол и отпущен без начальной скорости (), найдём для постоянных интегрирования значения: С₁ = 0, С₂ =. Тогда закон малых колебаний маятника при данных начальных условиях будет:

Следовательно, малые колебания физического маятника являются гармоническими. Период малых колебаний физического маятника, если заменить k его значением, определяется формулой:

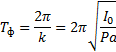
Полученные результаты охватывают и случай так называемого математического маятника, т.е. груза малых размеров (которые будем рассматривать как материальную точку), подвешенного на нерастяжимой нити длиной l, массой которой, по сравнению с массой груза, можно пренебречь (рис.57, б). Для математического маятника, т.к. он представляет собой систему, состоящую из одной материальной точки, очевидно, будет

.

Подставляя эти величины в равенство, найдем, что период малых колебаний математического маятника определяется формулой

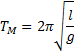
Из сравнения формул и видно, что при длине

период колебаний математического маятника совпадает с периодом колебаний соответствующего физического маятника.

Длина такого математического маятника, период колебания которого равен периоду колебаний данного физического маятника, называется приведенной длиной физического маятника. Точка K, отстоящая от оси подвеса на расстоянии , называется центром качания физического маятника (рис.57).

Замечая, что по теореме Гюйгенса , мы можем привести формулу к виду

Отсюда следует, что расстояние OK всегда больше чем OC = a, т.е. что центр качаний физического маятника всегда расположен ниже его центра масс.

Плоскопараллельное движение твердого тела.

Положение тела, совершающего, плоскопараллельное движение, определяется в любой момент времени положением полюса и углом поворота тела вокруг полюса. Задачи динамики будут решаться проще всего, если за полюс взять центр масс С тела (рис.11) и определять положение тела координатами X_C, Y_C и углом .

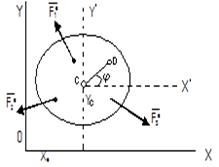
Рис.11

На рис.5 изображено сечение тела плоскостью, параллельной плоскости движения и проходящей через центр масс С. Пусть на тело действуют внешние силы , лежащие в плоскости этого сечения. Тогда уравнения движения точки С найдём по теореме о движении центра масс

,

а вращательное движение вокруг центра С будет определятся уравнением

т.к. теорема, из которой получено это уравнение, справедливо и для движения системы вокруг центра масс. В результате, проектируя обе части равенства на координатные оси, получим:

Эти уравнения представляют собой дифференциальные уравнения плоскопараллельного движения твёрдого тела. С их помощью можно по заданным силам определить закон движения тела или, зная закон движения тела, найти главный вектор и главный момент действующих сил.

При несвободном движении, когда траектория центра масс известна, уравнения движения точки С удобно составлять в проекциях на касательную τ и главную нормаль n к этой траектории. Тогда получим:

где - радиус кривизны траектории центра масс.

Пример 4. Однородный круглый цилиндр скатывается по наклонной плоскости (рис.12). Цилиндр совершает плоскопараллельное движение.

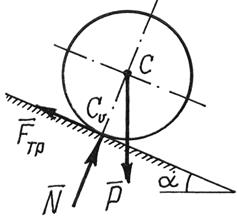
Рис.12

Решение. Так как и, значит, составим дифференциальное уравнение вращения относительно оси проходящей через мгновенный центр скоростей.

Момент инерции цилиндра относительно оси

Поэтому уравнение получится таким

Знак (–) указывает на направление углового ускорения – по часовой стрелке.

Обратим внимание на то, что реакции не вошли в уравнение.

Чтобы определить реакцию F_тр, составим еще одно дифференциальное уравнение вращения, относительно центральной оси С :

Отсюда

Конечно, . Чтобы тело катилось без скольжения должно выполняться условие или . Поэтому коэффициент трения скольжения должен удовлетворять условию .

Пример 5. Балочка АВ длиной l и весом Р падает, скользя концами по гладким поверхностям стены и пола (рис.13). Составим дифференциальное уравнение вращения.

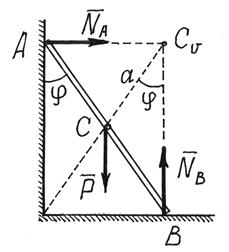
Рис.13

Решение. Здесь . Поэтому опять выгоднее составить дифференциальное уравнение вращения относительно оси . Тем более, что неизвестные реакции и не войдут в это уравнение.

Так как то уравнение получится таким: .

Отсюда

Пример 6. Тело, имеющее форму половины кругового цилиндра, катается по горизонтальной плоскости без скольжения (рис.14). Вес его – Р. Положение центра тяжести определяется расстоянием , момент инерции относительно оси О: I₀=0,5Mr²

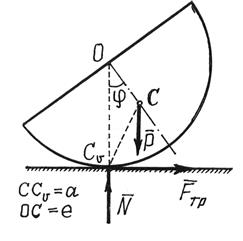
Рис.14

Решение. Поскольку неизвестны ни сила трения F_тр, ни нормальная реакция N, конечно следует составлять дифференциальное уравнение вращения относительно оси .

Момент инерции тела относительно оси по теореме Гюйгенса-Штейнера, , а I₀=I_C+Me², поэтому .

Количество движения

Составляем дифференциальное уравнение:

После подстановки значения a, получим

и, окончательно, подставив значение ,

Пример 7. Стержень качался как маятник, вращаясь в вертикальной плоскости вокруг шарнира О (рис.15). В момент, когда стержень был в вертикальном положении и угловая скорость его была , шарнир разрушился. Определим дальнейшее движение стержня.

Решение. Стержень начнет совершать плоскопараллельное движение. На рис.62 показано его промежуточное положение.

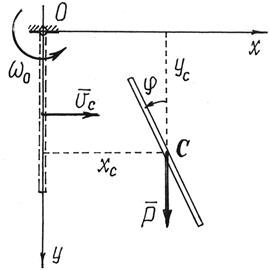
Рис.15

Составим дифференциальные уравнения движения.

Интегрируем их дважды:

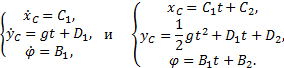
Начальные условия: при t = 0

Подставив их в последние шесть уравнений, получим

Тогда уравнения плоскопараллельного движения стержня

Например, стержень займет горизонтальное положение, , в момент когда центр масс его будет в точке с координатами

Сложное движение твердого тела и системы тел.

Пример 8. На гладкое проволочное кольцо радиуса R надет маленький шарик. Кольцо вместе с шариком вращается вокруг вертикальной оси, проходящей через диаметр кольца, с угловой скоростью ω. Где находится шарик?

Решение. Решение этой задачи можно осуществить, применяя разные системы отсчета - как инерциальную (ИСО), связанную с Землей, так и неинерциальную (НИСО), связанную с кольцом; различным может быть и выбор осей координат. Чтобы показать, что в любом случае состав операций, приведенный в алгоритмическом предписании, не зависит от выбора системы отсчета, будем указывать их номера.

Решение задачи в ИСО

1. Рассмотрим решение этой задачи в инерциальной системе отсчета, связанной с Землей (рис.16).

Рис.16

2. Шарик можно рассматривать как материальную точку, которая вращается вместе с кольцом с угловой скоростью ω.

3. На шарик действуют две силы: сила тяжести со стороны Земли mg и реакция кольца N. Поскольку по условию задачи кольцо гладкое, силой трения можно пренебречь.

4. Второй закон Ньютона в векторной форме имеет вид

5. Шарик движется по окружности радиуса r=R∙sinα с постоянной угловой скоростью ω. Его ускорение равно

и направлено к центру окружности C. Совместим с вектором ускорения ось х, ось у направим вертикально вверх, как показано на рисунке.

6. Запишем второй закон Ньютона в проекциях на оси координат:

7. Из (3) находим Подставляя это выражение и формулу (1) в уравнение (2), получаем

Из полученного уравнения находим следующие условия равновесия:

Это означает, что при вращении с малой угловой скоростью шарик подниматься не будет, равновесие соответствует значению . При вращении с большой угловой скоростью , что эквивалентно условию cosα<1, равновесное положение соответствует углу

Решение задачи в НИСО

1. Рассмотрим решение этой же задачи в неинерциальной системе отсчета, вращающейся с угловой скоростью ω (рис.17). В этой системе отсчета шарик покоится.

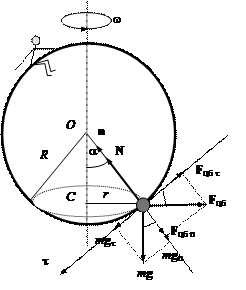
Рис.17

2. Кроме реальных сил взаимодействия, действующих на шарик - силы тяжести mg и нормального давления , следует ввести центробежную силу инерции F_цб, величина которой равна

Шарик не движется относительно кольца, следовательно, его ускорение равно нулю.

3. Второй закон Ньютона превращается в условие равновесия шарика в системе отсчета, связанной с кольцом:

4. Спроектируем векторное уравнение на тангенциальное τ (касательное к окружности) и нормальное n (перпендикулярное касательной) направления.

или с учетом (1)

Из уравнения (3) получим те же условия равновесия, что и ранее:

откуда

Пример 9. Внутри конуса, установленного в ракете, поднимающейся вертикально вверх с ускорением а₀, находится небольшое тело (рис.18). Конус имеет при вершине угол 2α и вращается вокруг своей оси с угловой скоростью ω. На каком максимальном расстоянии l от вершины конуса будет находиться тело, если коэффициент трения между телом и поверхностью конуса равен μ? Ось конуса совпадает с продольной осью ракеты.

Рис.18

Решение.

1. Система отсчета (наблюдатель находится на конусе) - неинерциальная. Относительно наблюдателя на Земле она движется вверх с ускорением а₀ и вращается с угловой скоростью ω.

2. Тело (материальная точка) неподвижна относительно конуса, вместе с конусом вращается, а вместе с ракетой движется равноускоренно с ускорением а₀.

3. На тело кроме реальных сил взаимодействия - силы тяжести mg, нормального давления N и силы трения F_тр,

следует ввести центробежную силу инерции F_цб, величина которой равна

и силу инерции, связанную с поступательным прямолинейным движением системы отсчета: F_ин = - mа₀. Модуль этой силы равен

Тело в выбранной системе отсчета неподвижно, его ускорение равно нулю.

4. Второй закон Ньютона превращается в условие равновесия:

5. Далее решение задачи очевидно: проектировать векторное уравнение на оси координат и разрешать полученную систему алгебраических уравнений. Оси координат указаны на рисунке.

6. Второй закон Ньютона в проекциях на оси координат имеет вид

7. Подставляя в уравнения (4) - (5) выражения (1) - (3), разрешаем систему относительно радиуса окружности

Следовательно, расстояние от вершины конуса до тела равно

Пример 10. На горизонтальной шероховатой поверхности лежит катушка ниток массы m. Ее момент инерции относительно собственной оси , где β - числовой коэффициент, R - внешний радиус катушки. Радиус намотанного слоя ниток равен r. Катушку без скольжения начали тянуть за нить с помощью постоянной силы F, направленной под углом α к горизонту. Найти модуль и направление ускорения оси катушки.

Решение. Рассмотрим два варианта решения этой задачи. Во-первых, движение катушки можно считать наложением двух видов движения: поступательного со скоростью центра масс и вращения вокруг оси симметрии. Соответственно, записываются два динамических закона: уравнение движения центра масс и уравнение динамики вращательного движения. Во-вторых, движение катушки можно представить как чисто вращательное движение вокруг мгновенной оси О, проходящей через точки касания катушки о горизонтальную поверхность. В этом случае достаточно одного динамического уравнения - уравнения вращательного движения.

Обратимся к первому варианту решения задачи. Движение катушки можно считать наложением двух видов движения: поступательного со скоростью центра масс и вращения вокруг оси симметрии.

Выбираем инерциальную систему отсчета, связанную с Землей.

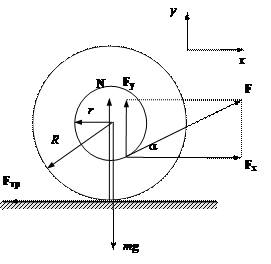
Рис.19

На катушку действуют Земля с силой тяжести mg, нить с силой F и горизонтальная поверхность с силами нормального давления N и трения F_тр.

Поскольку катушка движется без проскальзывания, то

Рассмотрим поступательное движение. Уравнение движения центра масс в векторной форме имеет вид

Оси координат указаны на рис.19. Спроектируем векторное уравнение на оси координат:

Рассмотрим вращательное движение. Уравнение динамики вращательного движения катушки относительно ее оси в векторной форме имеет вид

Моменты сил F и F_тр направлены вдоль оси вращения, но в противоположные стороны. Поэтому Учитывая, что M_mg=0, M_N=0, J=mR², запишем уравнение динамики вращательного движения в проекции на ось z, направленную вдоль оси вращения “от нас”:

Составим уравнение, связывающее кинематические величины, входящие в уравнения (1) и (3), a_c и ε. Для этого изобразим катушку в двух состояниях.

Рис.20

Из рис.20 видно, что перемещение центра катушки s_c при отсутствии проскальзывания равно длине дуги, на которую опирается угол поворота катушки φ вокруг оси С. Следовательно,

Продифференцируем это выражение дважды по времени

Учитывая определения линейного и углового ускорений

получим уравнение кинематической связи:

Систему уравнений (1) - (4) нетрудно разрешить относительно искомой величины:

Анализ полученного выражения приводит к заключению, что при ускорение оси катушки a_c>0 и катушка движется в направлении оси х. При ускорение a_c<0 и катушка движется в противоположном направлении. При катушка покоится a_c=0.

Рассмотрим второй вариант решения задачи - катушка вращается вокруг мгновенной оси О (рис.21).

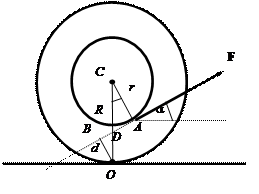
Рис.21

Относительно этой оси моменты силы тяжести mg, силы нормального давления N и силы трения F_тр равны нулю, так как линии действия этих сил проходят через мгновенную ось. Уравнение динамики вращательного движения примет вид

где J₀ - момент инерции относительно оси О. По теореме Штейнера

Плечо d силы F находим геометрически. Из треугольника ACD выразим гипотенузу CD через прилежащий катет AC = r:

Затем находим а из треугольника OBD

Подставляя (6) и (7) в (5), получаем

откуда выражаем угловое ускорение

Ускорение центра масс катушки a_c является тангенциальным ускорением точки С при вращении вокруг оси О, оно связано с угловым ускорением ε соотношением: . Следовательно, мы получаем прежнее выражение для ускорения центра масс

Данный способ описания облегчает анализ направления движения. Действительно, если линия действия силы проходит выше мгновенной оси О , то момент силы F вызывает вращение по часовой стрелке, катушка движется вправо (рис.22).

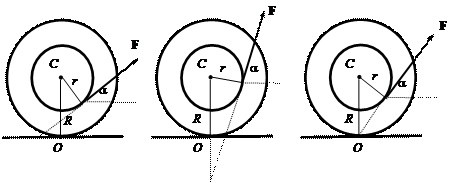
Рис.22

Если же линия действия силы проходит ниже оси О , момент силы F вызывает вращение против часовой стрелки, катушка движется влево.

Если линия действия силы F проходит через мгновенную ось О, катушка неподвижна, т.к. момент силы равен нулю. Из рисунка видно, что равновесию соответствует угол α, удовлетворяющий условию что согласуется с ранее полученным результатом.

Пример 11. В установке известны массы тел m₁ и m₂, коэффициент трения μ между телом m₁ и горизонтальной плоскостью, а также масса блока m, который можно считать однородным диском (рис.23). Скольжения нити по блоку нет. В момент t = 0 тело m₂ начинает опускаться. Пренебрегая массой нити и трением в оси блока, найти ускорения всех тел.

Рис.23

Решение. В системе тел, изображенной на рис.23, бруски движутся поступательно и их движение описывается вторым законом Ньютона:

Спроектируем эти уравнения на оси координат:

Блок массивный, поэтому для описания его вращения запишем основное уравнение динамики вращательного движения:

Учитывая, что момент инерции сплошного однородного диска равен , а модули моментов сил, действующих на блок,

спроектируем последнее векторное уравнение на ось z, направленную перпендикулярно плоскости рисунка “от нас” (направление оси соответствует направлению вектора углового ускорения):

Чтобы система уравнений была полной, в нее следует включить уравнения кинематической связи. Для ее записи изобразим систему тел в двух состояниях (рис.24) и найдем соотношение между перемещениями обоих грузов и углом поворота блока. Из условия нерастяжимости нити следует, что AA’=BB’=CC’, или

Рис.24

Дифференцируя это выражение дважды по времени, получаем уравнение связи между ускорениями:

Систему (1)-(5) с учетом соотношения нужно разрешить относительно ε и a. Из уравнения (2) N=m₁g, следовательно, . Тогда уравнение (1) перепишется в виде

Подставляя T₁ из (6), T₂ из (3) и из (5) в уравнение (4), получаем

откуда

Эта задача позволяет сделать вывод о натяжении нитей в приближении невесомого блока. Положив в формуле (4) m= 0, получаем: T₁=T₂, т.е. натяжение вдоль невесомой нити одинаково по обе стороны блока. Это условие постулировалось при решении ряда задач в школьном курсе физики.

Пример 12. Наклонная доска, составляющая с горизонтом угол 60°, приставлена к горизонтальному столу (рис.25). Два груза массой по 1 кг каждый соединены легкой нитью, перекинутой через невесомый блок, и могут перемещаться соответственно по доске и столу. Найти силу натяжения нити a и ускорение системы T, если коэффициент трения тел о поверхность доски и стола одинаков и равен 0,3.

Дано: m₁=m₂=m=1 кг, α=60°, μ=0,3

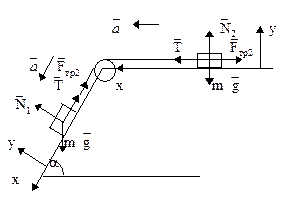
Рис.25

Решение. На рисунке укажем все силы, действующие на каждое тело.

Уравнение движения для любого тела

В проекциях на оси Х и Y:

I тело

x: ma=mg∙sinα - T-F_тр1

y: N₁-mg∙cosα=0,

но F_тр1=μN₁=μmg∙cosα, тогда

ma=mg∙sinα - T- μmg∙cosα. (1)

II тело

x: ma= T-F_тр1

y: N₂-mg =0,

но F_тр2=μN₂=μmg, тогда

ma= T- μmg. (2)

Решая систему уравнений (1) и (2),получим

T=m(a+μg).

a=2 м/с; Т=5 Н.

Пример 13. Две гири массами m₁=2 кг и m₂=1 кг соединены нитью и перекинуты через невесомый блок (рис.26). Найти ускорение, с которым движутся гири, и силу натяжения нити. Трением в блоке пренебречь.

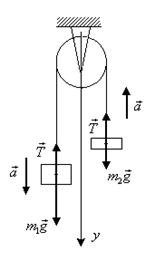
Рис.26

Решение. Условие невесомости и нерастяжимости нити позволяет сделать вывод о том, что сила натяжения нити на всех участках одинакова и грузы движутся с одинаковым ускорением, т.е. T=T₁=T₂; a=a₁=a₂. Запишем законы движения для каждого груза.

Выберем направление оси y вниз и спроецируем на нее силы и ускорения:

Отсюда

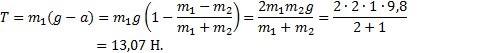
Пример 14. Три груза массами соединены невесомыми нерастяжимыми нитями (рис. 27). Нити переброшены через невесомые блоки, закрепленные на трапециевидном твердом теле ABCD массы . Первый груз перемещается вниз по закону , приводя в движение всю систему. Определить закон движения тела ABCD вдоль гладкой горизонтальной плоскости и его давление на эту плоскость. Угол BAD равен , в начальный момент времени система покоилась.

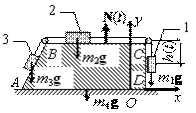
Рис.27

Решение. На данную систему (тело ABCD с закрепленными на нем блоками и грузами, соединенными нитями) действуют следующие внешние силы: вес тела , веса грузов и сила нормальной реакции гладкой плоскости N (см. рис. 27). Согласно теореме о движении центра масс,

(1)

где .

В проекции на горизонтальную ось Ox соотношение (1) дает: . Следовательно, . Постоянная C₁=0, так как в начальный момент времени система покоилась. Но тогда х_с = const или х_с(t) = х_с(0) для любого момента времени t, следовательно,

где – абсциссы центров масс грузов и тела.

Выберем начало O системы координат Oxy так, чтобы , т.е. так, что ось Oy проходит через центр масс тела ABCD в начальный момент времени. В этой системе отсчета координаты грузов и тела связаны соотношениями

.

Подставляя эти соотношения в уравнение (2), получим закон движения тела ABCD: . Знак "минус" означает, что призма перемещается влево относительно плоскости.

Давление тела ABCD на плоскость с точностью до знака совпадает с нормальной реакцией плоскости. Уравнение для ее определения получается, если спроектировать (1) на ось . Откуда

(3)

где ордината центра масс системы определяется соотношением

My_c = m₁y₁ + m₂y₂ + m₃y₃ + m₄y₄. (4)

Здесь – ординаты центров масс грузов и тела. Для нахождения y_c продифференцируем дважды по времени равенство (4), учитывая, что

,

.

Подставляя полученное в уравнение (3), находим

.

Движение тела с переменной массой.

Под точкой переменной массы подразумевается геометрическая точка, в которой сосредоточена конечная масса т, изменяющаяся во время движения по определенному закону.

Так, при движении масса ракеты изменяется за счет выбрасываемых из нее продуктов сгорания. Поступательное движение этой ракеты может быть легко сведено к изучению движения какой-либо ее характерной точки. Дифференциальные уравнения движения этой точки будут представлять собой дифференциальные уравнения движения точки переменной массы m(t). Другим примером тела переменной массы может служить рулон газетной бумаги, так как при разматывании его на валу печатной машины масса его уменьшается. Классическим примером динамической задачи, где необходимо учитывать изменения масс движущихся тел, является шахтный подъемник. При опускании груза в шахту длина подъемного каната, а следовательно, и его масса увеличиваются за счет уменьшения массы каната, навитого на барабане. При подъеме груза наблюдается обратное явление. Можно привести еще ряд примеров, когда масса тел при движении увеличивается. Так, при падении на Землю метеоритов масса Земли увеличивается. Масса Солнца в результате лучеиспускания уменьшается, а при присоединении космической пыли возрастает.

Основоположник механики тел переменной массы И. В. Мещерский (1859-1935) в основу своих исследований положил гипотезу близкодействия отбрасываемых частиц. При этом допускалось, что при отделении от тела частицы происходит удар, при котором за весьма малый промежуток времени отбрасываемая частица получает относительную скорость, и тогда дальнейшее взаимодействие отбрасываемой частицы с данным телом прекращается. Пользуясь этой гипотезой, И. В. Мещерский вывел основное уравнение движения точки переменной массы. Существенно подчеркнуть, что здесь речь идет о движении тел переменной массы в пределах классической механики. При этом масса тел определяется обычным путем и изменяется по заранее заданному закону. Поэтому переменная масса, которая рассматривается в данном разделе, не имеет ничего общего с переменной массой, фигурирующей в теории относительности.

Второй закон Ньютона в виде ma=F предполагает постоянство массы движущего тела. В тех случаях, когда масса тела изменяется (например, в ракетах в результате сгорания топлива) или при изменении соотношения между движущейся и неподвижной частями рассматриваемого тела, то производить расчеты по указанной формуле нельзя и следует воспользоваться другой записью второго закона Ньютона:

Отметим, что второй закон Ньютона в данной формулировке справедлив и для случая движения тела со скоростью, близкой к скорости света, то есть является основным законом релятивистской динамики.

Пример 15. Кобра массой m и длиной l поднимается вверх с постоянной скоростью v (рис.28). С какой силой кобра давит на пол?

Рис.28

Решение. Изменение импульса кобры в данном случае связано не с изменением скорости, а с изменением массы, участвующей в движении. Будем считать массу тела кобры равномерно распределенной по ее длине. За время dt движущаяся масса возрастает на величину

где dx - увеличение длины движущейся части кобры. Приращение импульса за это время составляет

Под действием каких сил происходит изменение импульса в данном случае?

На кобру действуют две силы: сила тяжести mg и сила реакции пола N. По третьему закону Ньютона кобра давит на пол с силой, равной N по абсолютному значению. Запишем второй закон Ньютона с учетом направлений сил и приращения импульса

Подставляя в него формулу (1) и учитывая определение скорости , находим искомую силу:

Рассмотрим теперь два примера, условия которых на первый взгляд почти не отличаются, но при более внимательном подходе оказываются существенно различными, вследствие чего примеры имеют разные решения.

Пример 16. Платформа массой m начинает двигаться под действием постоянной горизонтальной силы F. Из неподвижного бункера на нее высыпается песок. Скорость погрузки постоянна и равна μ (кг/с). Найти зависимость от времени скорости и ускорения платформы в процессе погрузки. Трение пренебрежимо мало.

Пример 17. Тележка с песком движется по горизонтальной поверхности под действием постоянной силы F, совпадающей по направлению с ее вектором скорости. При этом песок высыпается через отверстие в дне с постоянной скоростью μ (кг/с). Найти ускорение и скорость тележки в момент времени t, если в момент t = 0 тележка с песком имела массу m₀ и скорость ее была равна нулю. Трением пренебречь.

Решение. В этих примерах рассматривается движение тел переменной массы, в первой задаче движущаяся масса возрастает, во второй - уменьшается. В обоих примерах тела движутся под действием постоянной силы при отсутствии трения. Для тел переменной массы обычно применяют второй закон Ньютона в виде

Отметим, что в данном случае это уравнение записано для тележки (или платформы) с песком. Однако необходимо обсудить, что влияет на изменение импульса в первом и во втором случаях.

Поскольку бункер неподвижен (пример 16), песок, ссыпаясь вертикально на платформу, не изменяет ее горизонтального импульса. Импульс платформы с песком изменяется (возрастает) благодаря действию постоянной силы F. Изменение импульса за время dt равно dp=Fdt. Интегрирование этого соотношения дает p-p₀=F(t-t₀) или, учитывая, что в начальный момент времени платформа покоилась (t₀=0, p₀=0), p=Ft. Отсюда Учитывая зависимость массы от времени m=m₀+μt, получаем

Используя определение ускорения , находим его зависимость от времени

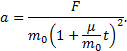
Во второй задаче (пример 17) импульс тележки с песком изменяется не только вследствие действия силы, часть импульса “уносится” вместе с высыпающимся песком, который перестает “принадлежать” тележке. Если в момент времени t тележка (и песок, находящийся на ней) имели скорость v и за время dt высыпалась масса песка dm, имеющая импульс dmv, то импульс тележки за это же время изменился на

В данном случае dm - величина отрицательная (масса песка на тележке убывает), высыпание песка из движущейся тележки приводит к уменьшению импульса на dmv, сила, действующая в направлении движения, увеличивает импульс тележки на величину, равную Fdt.

Из определения импульса p=mv следует, что его изменение

dp=dm∙v+m∙dv.

Таким образом,

dm∙v+m∙dv=F∙dt+dm∙v,

откуда

Учитывая зависимость массы от скорости

и определение ускорения

получаем зависимость ускорения от времени

Изменение скорости за время dt равно

Интегрирование этого выражения приводит к искомой зависимости скорости от времени:

Совместное применение законов динамики и методов решения кинематических задач.

Пример 18. На небольшое тело массы m, лежащее на гладкой горизонтальной поверхности (рис.29), в момент t=0 начала действовать сила, зависящая от времени по закону F = kt, где k - постоянная. Направление этой силы все время составляет угол α с горизонтом. Найти скорость тела в момент отрыва от плоскости и путь, пройденный телом к этому моменту.

Рис.29

Решение. Эта несложная с точки зрения применения законов динамики задача интересна тем, что в ней рассматривается результат действия переменной силы F. Возрастающая вертикальная составляющая силы F_y приводит к уменьшению силы N взаимодействия тела и горизонтальной опоры, а в момент отрыва N = 0.

На тело действует Земля с силой mg, горизонтальная опора с силой нормального давления N (сила трения пренебрежимо мала, т.к. поверхность по условию задачи гладкая) и переменная сила F, модуль которой пропорционален времени: F = kt.

По второму закону Ньютона

Спроектируем векторное уравнение на оси координат:

Уравнение (1) позволяет найти ускорение как функцию времени:

Определение пути, пройденного телом, и скорости в момент отрыва - это кинематическая задача первого класса. Воспользуемся определением ускорения и найдем изменение скорости за время dt:

Проинтегрируем это уравнение по времени от t = 0 до произвольного момента времени t и учтем, что начальная скорость тела v₀=0:

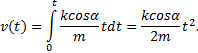
Установив зависимость скорости от времени, можно с помощью определения скорости получить зависимость координаты х от времени t.

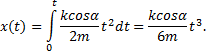
Рассмотрим момент отрыва тела от поверхности (задача четвертого класса - применение уравнений к конкретным состояниям). В уравнении (2) положим N = 0 и найдем, в какой момент времени произойдет отрыв:

Подставляя это выражение в кинематические уравнения движения, получим

Пример 19. Сплошному однородному цилиндру массы m и радиуса R сообщили вращение вокруг оси с угловой скоростью ω₀ (рис.30). Затем его положили боковой поверхностью на горизонтальную плоскость и предоставили самому себе. Коэффициент трения между цилиндром и плоскостью равен μ. Найти время, в течение которого движение цилиндра будет проходить со скольжением, а также скорость, которую приобретет цилиндр к этому моменту.

Рис.30

Решение. Силы, действующие на цилиндр, очевидны: сила тяжести mg, сила нормального давления N и сила трения F_тр. Последняя направлена в сторону, противоположную вектору скорости в точках касания цилиндра, и тормозит его вращение.

Следует обратить внимание на следующее обстоятельство: при проскальзывании цилиндра сила трения

Как только цилиндр начинает катиться без проскальзывания, это соотношение применять нельзя.

Цилиндр участвует в двух движениях: поступательном перемещении вместе с центром масс, которое описывается уравнением движения центра масс

и вращении вокруг оси, проходящей через центр масс, для которого справедливо уравнение динамики вращательного движения

Спроектируем векторные уравнения на оси координат:

Учитывая, что перепишем уравнение (3) в виде

Из уравнения (2) N=mg, F_тр=μmg. Из уравнения (1)

из уравнения (3а)

Отсутствие проскальзывания означает, что при перемещении центра цилиндра на расстояние s_c цилиндр повертывается на угол (рис.31).

Рис.31

Однократное дифференцирование этого соотношения по времени дает связь между скоростью центра масс и угловой скоростью вращения

Поскольку при движении с постоянным ускорением законы зависимости скорости от времени известны, применим их к движению данного цилиндра. Центр масс перемещается равноускоренно, его начальная скорость равна нулю, следовательно,

Вращение цилиндра является равнозамедленным, его начальная угловая скорость равна ω₀, следовательно,

Решая совместно систему кинематических уравнений (4)-(6), находим время, в течение которого цилиндр движется со скольжением

а также скорость цилиндра, которую он приобретает к этому моменту

Пример 20. Небольшой шарик массы m, подвешенный на нити, отвели в сторону так, что нить образовала прямой угол с вертикалью, а затем отпустили (рис.32). Найти: 1) полное ускорение шарика и натяжение нити в зависимости от угла отклонения нити φ от вертикали; 2) угол φ между нитью и вертикалью в момент, когда вектор полного ускорения направлен горизонтально.

Рис.32

Решение. Шарик движется по окружности под действием постоянной силы тяжести, равной mg, и под действием переменной, зависящей от угла φ силы натяжения нити T.

Запишем второй закон Ньютона в векторной форме:

В данной задаче целесообразно векторное уравнение проектировать на тангенциальное и нормальное направления:

Поскольку обе составляющие ускорения зависят от угла φ, необходимо выразить их через угловые величины:

(Знак “минус” связан с уменьшением угловой скорости ω при увеличении угла φ).

Решение уравнения (2) позволяет определить зависимость угловой скорости от угла. Подставляя в (2), приходим к дифференциальному уравнению, содержащему две разделяющиеся переменные ω и φ:

Разделяя переменные и интегрируя от ω₀=0 до ω и от φ₀=π/2 до φ,

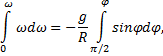
получаем , откуда выражаем зависимость угловой скорости от угла

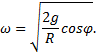
Подставляя нормальное ускорение в формулу (1),

находим натяжение нити в зависимости от угла φ:

Подставляя выражения для нормального и тангенциального ускорений a_n=2g∙cosφ и a_τ=g∙sinφ в формулу , получаем величину полного ускорения

Теперь ответим на второй вопрос задачи (рис.33). Вектор полного ускорения a направлен горизонтально при условии, что его составляющие связаны соотношением . Подстановка в это выражение a_n=2g∙cosφ и a_τ=g∙sinφ приводит к условию , то есть

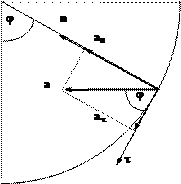
Рис.33

Следовательно, вектор полного ускорения направлен горизонтально, если нить, на которой подвешен шарик, составляет с вертикалью угол, равный

Совместное применение законов динамики и законов сохранения. Выбор способа решения.

Пример 21. Небольшое тело А начинает скользить с вершины гладкой сферы радиуса R. Найти угол φ, соответствующий точке отрыва тела от сферы, и скорость в момент отрыва (рис.34).

Рис.34

Решение. Тело А перемещается из состояния I в состояние II под действием двух сил - силы тяжести mg и силы нормального давления N (рис.35). Поскольку характер сил известен, можно решить задачу динамическим способом - применить второй закон Ньютона. С другой стороны, поскольку сила тяжести потенциальная, а сила нормального давления работы не совершает, энергия тела не изменяется, то есть можно воспользоваться законом сохранения энергии.

Рис.35

Рассмотрим оба способа решения задачи.

Динамический способ

По второму закону Ньютона

Спроектируем это векторное уравнение на нормальное и тангенциальное направления

Учитывая, что где ω - угловая скорость, ε - угловое ускорение, перепишем уравнения (1) - (2) в виде:

Откуда

то есть получена зависимость углового ускорения ε от угла φ. Далее следует решить кинематическую задачу по преобразованию уравнений третьего класса. Дополним уравнение (4) соотношениями

Из формулы (5) выразим и подставим в выражение (6), которое, в свою очередь, подставим в уравнение (4):

Из последнего выражения следует, что

Интегрирование уравнения

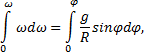
приводит к следующему выражению:

Подставим в уравнение (3), которое с учетом, что при отрыве сила нормального давления N=0, примет вид :

Из последнего уравнения получим

Выражение для угловой скорости в момент отрыва тела от поверхности сферы примет вид

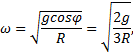
а для линейной скорости –

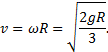
Сочетание энергетического и динамического подходов

Применим закон сохранения энергии. В состоянии I тело обладает потенциальной энергией

в состоянии II – кинетической

Поскольку , то

или

Нормальное ускорение можно выразить через линейную скорость как Тогда второй закон Ньютона в проекции на направление нормали для состояния II примет вид , или

Приравнивая выражения (7) и (8), , приходим к полученному ранее выражению Видно, что применение закона сохранения энергии целесообразнее решения уравнения (2).

Пример 22. Небольшой брусок начинает скользить по наклонной плоскости, составляющей угол α с горизонтом (рис.36). Коэффициент трения зависит от пройденного пути х по закону μ=kx, где k – постоянная. Найти путь, пройденный бруском до остановки.

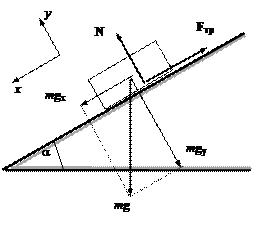
Рис.36

Решение.

Применение законов динамики

В данной задаче рассматривается движение под действием переменной результирующей силы.

На брусок действует Земля с силой тяжести mg и наклонная плоскость с силой нормального давления N и силой трения F_тр, величина которой равна

По второму закону Ньютона в векторной форме имеем:

Спроектируем это векторное уравнение на оси координат, указанные на рисунке,

Разрешая полученную систему уравнений относительно ускорения, получим зависимость ускорения от координаты х:

Далее решается кинематическая задача, связанная с преобразованием уравнений (задача третьего класса). Воспользуемся определениями скорости и ускорения

v = dx/dt, a = dv/dt,

и исключим переменные a и dt. В результате получим дифференциальное уравнение с разделяющимися переменными v и х:

Интегрируя это уравнение от момента, соответствующего началу движения (v₀=0, x₀=0) до остановки (v_ост=0, x=x_ост), получим

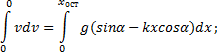
откуда искомая координата остановки равна

(корень x_ост=0 соответствует началу движения).

Энергетический способ

Значительно чаще эта задача решается с помощью закона изменения энергии.

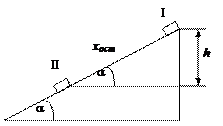
Рис.37

В состоянии I (рис.37) тело обладает потенциальной энергией

в состоянии II (рис.37) - как кинетическая, так и потенциальная энергия равна нулю

Энергия изменяется вследствие работы, совершаемой силой трения:

величина силы трения, как отмечалось раньше, составляет

Как видно из формулы, сила трения зависит от пройденного расстояния (координаты х). При перемещении на расстояние dx совершается работа

Полная работа до остановки составит

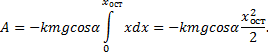
Подставим полученные выражения в применяемый закон:

и выразим искомую величину - путь, пройденный телом до остановки,

Видно, что и в этом случае энергетический способ решения задачи оказывается более предпочтительным.

Решение задач различными способами.

В существующих учебных пособиях каждая задача решается, как правило, одним способом, что приводит к неверному представлению о существовании единственно возможного пути решения конкретной задачи. Убедимся, что это не так.

Пример 23. На сплошной однородный цилиндр симметрично намотаны две тонкие нерастяжимые и невесомые нити, свободные концы которых закреплены (рис.38). Под действием силы тяжести цилиндр, вращаясь, опускается вниз. Определить ускорение а_с, с которым перемещается центр масс этого цилиндра.

Рис.38

Решение. На цилиндр действуют сила тяжести mg, точкой приложения которой можно считать центр масс цилиндра, и две одинаковые по величине силы натяжения нити Т.

Применение законов динамики. Вариант 1

Рассмотрим движение цилиндра как наложение двух видов движения: перемещение цилиндра как целого с ускорением, равным ускорению центра масс и вращение вокруг оси, проходящей через центр масс (рис.39). Поэтому применяются два закона динамики, каждый из которых описывает соответствующий вид движения.

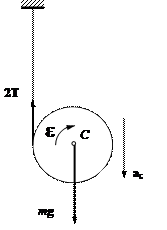
Рис.39

Первый вид движения подчиняется уравнению движения центра масс:

второй - уравнению динамики вращательного движения:

Момент инерции цилиндра относительно оси, проходящей через центр масс составляет , моменты M_mg=0, M_2T=2TR. С учетом этих соотношений уравнение (2) принимает вид

Уравнение кинематической связи, как и при решении других подобных ранее рассмотренных задач, имеет вид

Разрешим систему уравнений (1) - (3) относительно искомой величины. Выразим из (3) угловое ускорение и подставим в формулу (2):

Полученную из последнего выражения силу натяжения нити подставим в (1) откуда и получим искомое ускорение

Применение законов динамики. Вариант 2

Движение цилиндра можно рассматривать как чисто вращательное относительно мгновенной оси О с угловым ускорением ε (рис.40).

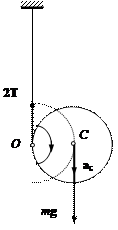
Рис.40

Уравнение динамики вращательного движения в данном случае имеет вид

в котором момент инерции относительно оси вращения находится по теореме Штейнера Подстановка выражения дает

Моменты сил относительно оси О также имеют иной вид, отличающийся от предыдущего случая: M_mg=mgR, M_2T=0. Ускорение центра масс а_с является тангенциальным при движении точки С по окружности радиуса R, следовательно Подстановка полученных выражений в уравнение (1) приводит к тому же выражению искомого ускорения

Применение законов динамики во второй формулировке

Как в предыдущем случае, будем рассматривать движение цилиндра как чисто вращательное относительно мгновенной оси О (рис.41).

Рис.41

Уравнение динамики вращательного движения можно представить в ином виде, а именно, скорость изменения момента импульса равна сумме моментов сил, действующих на тело:

Момент импульса цилиндра относительно оси О , моменты сил M_mg=mgR, M_2T=0, поэтому

Учитывая определение углового ускорения и формулу связи приходим к выражению для ускорения цилиндра

Безусловно, законы динамики во второй формулировке можно применять и при интерпретации движения цилиндра как сочетания поступательного и вращательного.

Применение закона сохранения энергии. Вариант 1

Закон сохранения энергии, как и законы динамики, можно применять по разному, в зависимость от описания движения цилиндра.

Рассмотрим первый способ, при котором движение цилиндра рассматривается как сложное. Пусть центр масс за время t опустился на расстояние h. В начальном состоянии цилиндр обладал потенциальной энергией , спустя время t - кинетической, , причем . Угловая скорость вращения относительно оси, проходящей через центр масс связана с линейной скоростью центра масс соотношением Тогда

Подставим полученные выражения в закон сохранения энергии

Учтем, что при движении с постоянным ускорением Тогда последнее выражение принимает вид из которого легко получить ускорение цилиндра

Применение закона сохранения энергии. Вариант 2

Рассмотрим вращение цилиндра относительно мгновенной оси с угловой скоростью ω. Скорость центра масс связана с угловой скоростью соотношением . В данном случае выражение кинетической энергии принимает вид По закону сохранения энергии с учетом соотношений получается прежний ответ.

Применение закона изменения момента импульса

Рассмотрим движение цилиндра как чисто вращательное относительно мгновенной оси О. Закон изменения момента импульса имеет вид

В начальном состоянии момент импульса цилиндра L_I=0, спустя время t после начала движения , моменты внешних сил M_mg=mgR, M_2T=0; поэтому

или

Учитывая, что , и определение ускорения , находим ускорение цилиндра

Применение законов изменения импульса и момента импульса

Если описывать сложное движение цилиндра, то, кроме закона изменения момента импульса, необходимо применить и закон изменения импульса.

В начальном состоянии момент импульса цилиндра относительно оси, проходящей через центр масс L_I=0, спустя время t после начала движения , моменты внешних сил M_mg=0, M_2T=2TR; поэтому

Закон изменения импульса примет вид

Исключая из системы уравнений силу натяжения нити Т и учитывая, что , приходим к выражению

Здесь представлено семь способов решения задачи. Это не означает, что любую задачу можно решить множеством способов. Иногда существует один единственно возможный путь решения, например в том случае, когда недостаточно сведений о характере взаимодействия тел в системе. В частности, это относится к описанию процессов взрыва или удара. Тем не менее, иметь представление о существующих возможностях весьма полезно.

Применение неинерциальной системы отсчета.

Пример 24. Плоскую спираль из жесткой гладкой проволоки, расположенную в горизонтальной плоскости, вращают с постоянной угловой скоростью ω вокруг неподвижной вертикальной оси О (рис.42). По спирали без трения скользит небольшая муфта массой m. Найти ее скорость относительно спирали v’ как функцию расстояния r от оси вращения, если муфта начала двигаться от этой оси со скоростью .

Рис.42

Решение. В условии задачи как известная величина (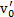), так и искомая (v’) заданы в системе отсчета, связанной со спиралью. На муфту действуют реальные силы тяжести mg и реакции со стороны спирали N. Силой трения пренебрегаем, так как проволока гладкая. Поскольку муфта движется относительно вращающейся системы отсчета, в перечень сил следует включить как центробежную силу F_цб, так и кориолисову силу инерции F_кор. Выражения для сил инерции имеют вид

Центробежная сила направлена от оси вращения, кориолисова сила согласно правилу векторного произведения направлена перпендикулярно векторам и ω (рис.43).

Рис.43

Сила тяжести, сила реакции спирали и кориолисова сила работы не совершают, так как они перпендикулярны к направлению перемещения. Поэтому изменение кинетической энергии муфты происходит только за счет работы центробежной силы

Выражения для кинетической энергии в состояниях, о которых говорится в условии задачи, имеют вид

Получим выражение для работы центробежной силы. При перемещении на расстояние ds совершается элементарная работа , где α - угол между векторами силы и перемещения. Проекция вектора перемещения на направление вектора силы равна dr=dscosα. Поэтому с учетом выражения для центробежной силы получаем элементарную работу После интегрирования находим выражение для полной работы

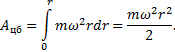
Подставляя выражения для кинетической энергии и работы в формулу (1)

находим скорость муфты относительно спирали как функцию расстояния от оси вращения:

Решение нестандартных задач.

Пример 25. Тело массы m₁ = 1 кг скользит без трения по гладкому горизонтальному столу и въезжает на подвижную горку массы m₂ = 5 кг. Высота горки H = 1,2 м. Трение между столом, горкой и телом отсутствует. Найти конечные скорости тела и горки. Начальная скорость тела v₀ = 5 м/с.

Примечания: 1) Обратить внимание на анализ физической ситуации, описанной в условии задачи. 2) Обратить внимание на зависимость поведения механической системы от ее параметров и начальных условий.

Решение. Из условия задачи неясно, перевалило тело горку или, поднявшись на некоторую высоту, скатилось назад. Поэтому сформулируем и решим вспомогательную задачу: определим максимальную высоту h, на которую тело может подняться. Если h<H, то тело скатывается назад, при h>H - переваливает через горку.

При отсутствии трения полная механическая энергия системы “горка + тело” сохраняется, поскольку сила реакции со стороны стола направлена вертикально, и ее работа равна нулю. В начальном состоянии I горка неподвижна (рис.44), движется только тело со скоростью v₀, его кинетическая энергия равна Будем считать потенциальную энергию системы в рассматриваемом состоянии равной нулю. Тогда полная механическая энергия системы равна кинетической энергии тела:

Рис.44

Когда тело въезжает на горку, его скорость уменьшается, а скорость горки возрастает. В момент, когда тело достигает максимальной высоты подъема h (состояние II) (рис.45), оно движется вместе с горкой с некоторой скоростью v, кинетическая энергия системы равна Учитывая, что тело массы m₁ приобретает потенциальную энергию запишем выражение для полной энергии в этом состоянии:

Рис.45

Согласно закону сохранения механической энергии W_I=W_II имеем

Это уравнение содержит две неизвестные величины v и h. Необходимо составить еще одно уравнение.

Внешние силы, действующие на тело и горку (силы тяжести и сила реакции стола) направлены вертикально. Импульс системы как в первом состоянии p_I=m₁v₀, так и во втором – p_II=(m₁+m₂)v, направлен горизонтально, внешние силы в этом направлении не действуют. Следовательно, импульс системы сохраняется, то есть p_I=p_II, или

Полученную систему уравнений легко разрешить. Из уравнения (2) выразим скорость и подставим в уравнение (1):

Найдем максимальную высоту подъема тела:

Таким образом, тело, поднявшись на высоту h<H, не перевалило горку, а скатилось назад.

Обозначим конечные скорости тела и горки через v₁ и v₂. Рассмотрим состояния I и III (рис.46) и применим законы сохранения энергии и импульса:

Рис.46

Система уравнений (3) - (4) является замкнутой, то есть число уравнений равно числу неизвестных. Выразим v₂ из уравнения (4)

и подставим в уравнение (3). В результате получится квадратное уравнение относительно v₁:

Откуда

Видно, что система уравнений имеет два решения.

Первое решение соответствует рассматриваемому случаю (поэтому скорость тела v₁ получилась отрицательной). Второе решение описывает ситуацию, когда тело перевалило через горку и продолжает двигаться в том же направлении с прежней скоростью v₀, а горка осталась неподвижной.

Пример 26. На гладкой горизонтальной плоскости лежит небольшая шайба и тонкий однородный стержень длины l, масса которого в n раз больше массы шайбы. Шайбе сообщили скорость v - в горизонтальном направлении перпендикулярно к стержню, после чего она испытала упругое соударение с концом стержня. Найти скорость шайбы и угловую скорость стержня после столкновения. При каком значении n скорость шайбы после столкновения будет равна нулю; изменит направление на противоположное?

Решение. Обозначим массу шайбы через m₁, массу стержня - m₂. Согласно условию m₂ = nm₁. Рассмотрим процесс упругого удара, в результате которого стержень приводится в движение. Это движение можно рассматривать как наложение двух простых видов: поступательного со скоростью центра масс стержня v₂ и вращательного с угловой скоростью ω относительно оси, проходящей через центр масс.

На систему тел “шайба + стержень” действуют силы тяжести и нормального давления со стороны горизонтальной поверхности. Эти силы направлены вертикально в противоположные стороны и уравновешивают друг друга. Силами трения согласно условию задачи можно пренебречь. Во время столкновения на каждое тело системы действует упругая сила, являющаяся внутренней.

Изменение импульса и момента импульса обусловлено только внешними силами. Равнодействующая внешних сил тяжести и нормального давления равна нулю, поэтому для системы тел выполняется закон сохранения импульса

где v_1x - проекция скорости шайбы после удара на направление ее первоначального движения.

Суммарный момент двух противоположно направленных сил, одинаковых по абсолютному значению и приложенных в одной точке, относительно любого центра или любой оси равен нулю. Следовательно, для рассматриваемой системы тел выполняется закон сохранения момента импульса

где J - момент инерции стержня относительно оси, проходящей через его центр,

При абсолютно упругом ударе диссипативных процессов не происходит, и имеет место закон сохранения энергии

Разрешим систему уравнений (1)-(3) относительно неизвестных v_1x, v₂ и ω. С учетом выражения для момента инерции стержня и соотношения между массами шайбы и стержня приведем ее к виду

Из уравнения (5) выразим проекцию скорости шайбы через угловую скорость

из сравнения уравнений (4) и (5) найдем скорость центра масс стержня как функцию ω

Подставляя полученные выражения в уравнение (6) и разрешая его относительно ω, находим угловую скорость стержня

и проекцию скорости шайбы

Нетрудно видеть, что при n = 4 скорость шайбы будет равна нулю (v_1x=0), при n > 4 шайба изменит направление движения на противоположное (v_1x<0).

Решение многоходовых задач.

Ряд задач требует применения большого количества формул - законов, соотношений, такие задачи называют многоходовыми.

Пример 27. Материальная точка массой m движется по дуге окружности радиусом R так, что ее криволинейная координата изменяется по закону . Определить зависимость от времени: 1) момента силы, действующей на точку; 2) момента импульса точки; 3) мгновенной мощности.

Решение.

1. Связь между угловой координатой и длиной дугой окружности имеет вид

2. Определение угловой скорости:

3. Определение углового ускорения:

4. Уравнение динамики вращательного движения: , где - момент инерции материальной точки,

5. Связь между моментом импульса и угловой скоростью:

6. Выражение для элементарной работы при вращательном движении: dA=Mdφ.

7. Определение мгновенной мощности:

Таким образом, мы пришли к выводу, что момент силы пропорционален первой степени времени, момент импульса пропорционален квадрату времени, мгновенная мощность пропорциональна кубу времени.

Ответы на вопросы, поставленные в условии задачи, выделены подчеркиванием.

Пример 28. Твердое тело начинает вращаться вокруг неподвижной оси. Положительные углы поворота отсчитываются по часовой стрелке. На рис.47 приведен график зависимости углового ускорения ε от времени t.

1) Укажите направление вращения через 2, 3, 4, 5, и 6 секунд после начала движения; 2) Сравните значения кинетической энергии в моменты времени 1 с и 4 с.

Рис.47

Решение. Направление вращения определяется знаком угловой скорости: если 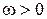, тело вращается по часовой стрелке, при 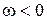- против часовой стрелки.

Изобразим схематически ход решения задачи.

Выпишем формулы, соответствующие каждому переходу и проанализируем их.

1. Запишем определение углового ускорения: ε=dω/dt и выразим изменение угловой скорости за бесконечно малый промежуток времени dt: dω=εdt (рис.48). Геометрически dω выражается площадью прямоугольника высотой ε и шириной dt.

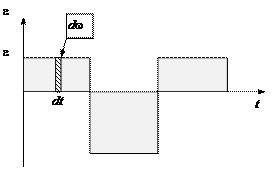
Рис.48

Проинтегрируем это выражение:

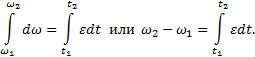
Геометрически интеграл можно интерпретировать как площадь. При этом следует иметь в виду, что на участках, где ε>0, интеграл, а следовательно, и приращение угловой скорости положительны, где ε<0 - отрицательны.

По условию задачи в начальный момент времени угловая скорость равнялась нулю, следовательно, зависимость угловой скорости от времени можно представить в виде

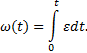
Вычислим геометрически значения угловой скорости в указанные моменты времени, их значения для каждого состояния указаны на соответствующем рисунке (рис.49).

2. Кинетическая энергия вращательного движения рассчитывается по формуле: где J - момент инерции. Для указанных состояний кинетическая энергия принимает значения , . Видно, что W_k4>W_k1 в 4 раза.

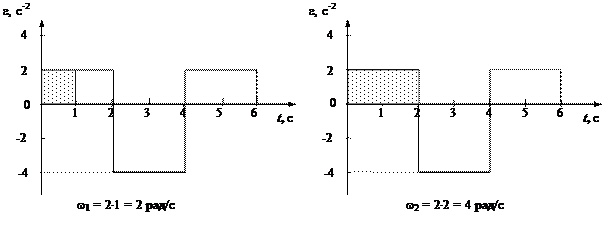
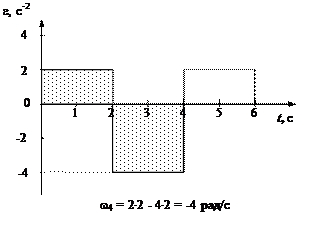
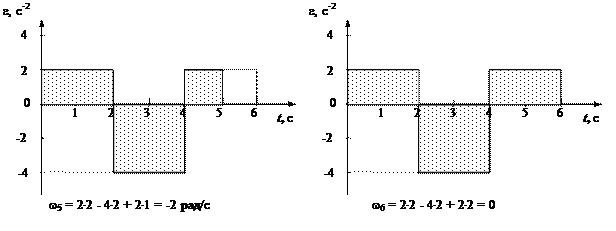
Рис.49

Вопросы для самопроверки

- Что называется силой инерции материальной точки?

- Какая система отсчета называется инерциальной?

- Какая система отсчета не является инерциальной?

- Какое движение точки называется относительным?

- Записать основной закон относительного движения точки.

- Какое движение точки называтся переносным?

- Что называется переносной силой инерции?

- Каким образом можно ввести понятие о силе инерции? Напишите формулу, выражающую силу инерции материальной точки.

- Чему равна и как направлена переносная сила инерции, если переносное движение является поступательным?

- Как определяется переносная сила инерции, если переносное движение является равномерным вращением вокруг неподвижной оси?

- Что называется силой инерции Кориолиса?

- Как направлена сила инерции Кориолиса?

- Записать модуль силы инерции Кориолиса.

- Сформулируйте принцип Даламбера для механической системы.

- Приведите определения главного вектора и главного момента сил инерции относительно центра.

- Какая механическая система называется динамически уравновешенной?

- В каком случае динамические составляющие подпятника и подшипника обращаются в нуль?

- В чем заключается принцип Даламбера для материальной точки?

- Сформулируйте принцип Даламбера для несвободной механической системы.

- Как вычисляется главный вектор и главный момент сил инерции тела при различных случаях его движения?

- Как определяются динамические реакции опор на ось быстро вращающегося тела?

- При соблюдении каких условий динамические реакции опор на ось быстро вращающегося тела не отличаются от статических реакций?

- Каким условиям удовлетворяют в любой момент времени главные векторы внешних задаваемых сил, реакции связей и сил инерции точек несвободной механической системы и главные моменты этих сил относительно любого неподвижного центра?

- Каковы модуль и направление главного вектора сил инерции механической системы?

- К чему приводятся силы инерции точек твердого тела:

а) при поступательном движении тела;

б) при вращении тела, имеющего плоскость материальной симметрии, вокруг неподвижной оси, перпендикулярной этой плоскости;

в) при плоском движении тела, имеющего плоскость материальной симметрии?

- При каких условиях динамические давления вращающегося тела на опоры равны нулю?

- Каково число и каков вид уравнений, выражающих принцип Даламбера для несвободной механической системы в проекциях на оси координат, в случаях, когда задаваемые внешние силы, реакции связей и силы инерции материальных точек твердого тела образуют:

а) плоскую систему параллельных сил;

б) систему сил, произвольно расположенных на плоскости;

в) систему параллельных сил в пространстве;

г) произвольную систему сил в пространстве?

- Каковы дифференциальные уравнения поступательного движения твердого тела?

- По какой формуле вычисляется кинетический момент твердого тела, вращающегося вокруг неподвижной оси, относительно этой оси?

- Какой вид имеет дифференциальное уравнение вращения твердого тела вокруг неподвижной оси?

- При каких условиях тело вращается вокруг неподвижной оси: а) ускоренно, б) равномерно, в) замедленно?

- Мерой чего является момент инерции твердого тела относительно оси?

- Записать дифференциальные уравнения движения материальной точки относительно системы координат, движущейся поступательно.

- Записать дифференциальные уравнения движения точки относительно системы координат, совершающей вращение вокруг неподвижной оси.

- Каковы основные типы задач, которые можно решать с помощью дифференциального уравнения вращения тела вокруг неподвижной оси?

- Какое положение механики иллюстрируется с помощью скамейки Жуковского?

- Что называют приведенной длиной, центром и осью качания физического маятника?

- По какой формуле вычисляется приведенная длина физического маятника?

- Каким свойством обладает ось привеса и ось качаний физического маятника?

- По какой формуле вычисляется период малых колебаний физического маятника?

- Назовите способы опытного определения моментов инерции твердых тел и укажите, в чем заключается их сущность.

- Сформулируйте теорему о зависимости между кинетическими моментами механической системы относительно неподвижного центра и относительно центра масс системы в векторной форме и в проекциях на оси координат.

- Как формулируется теорема об изменении кинетического момента механической системы в относительном движении по отношению к центру масс в векторной форме и в проекциях на оси координат?

- Почему сила тяжести не влияет на изменение кинетического момента механической системы относительно центра масс и относительно любой оси, проходящей через центр масс системы?

- Почему кинетический момент Солнечной системы относительно ее центра масс не изменяется?

- Какой вид имеют дифференциальные уравнения плоского движения твердого тела и на основании каких теорем они получены?

- Каким видом дифференциальных уравнений плоского движения твердого тела удобно пользоваться, если задана траектория центра масс тела?

- Каковы дифференциальные уравнения движения свободного твердого тела?

- При каких условиях движение свободного твердого тела является поступательным?

- По каким формулам вычисляются кинетические моменты твердого тела относительно неподвижной точки и относительно координатных осей при его сферическом движении?

- Чему равны кинетические моменты твердого тела относительно главных осей инерции, проведенных из неподвижной точки тела, при его сферическом движении?

- Какой вид имеют динамические уравнения Эйлера?

- Принцип Даламбера формулируется следующим образом:

1) при движении системы сумма работ всех активных сил и сил инерции системы равны нулю;

2) в каждый момент времени заданные силы и реакции связей, действующие на материальную точку (тело) как бы уравновешиваются силой инерции;

3) сумма работ всех внешних и внутренних сил, приложенных к системе равна изменению количества движения системы.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00