Главная

Тема 2. Механика классической Греции. Два вида движения: естественное и насильственное. Аристотель и параллелограмм скоростей

Началом расцвета механики как науки можно считать XVII век – век бурного развития математического естествознания. Именно тогда сформировались основные законы классической механики. Однако зарождение механических знаний относится к глубокой древности, а термин «механика» применялся в античном мире. Правда, ему в течение долгого времени, по крайней мере до середины XVII в., придавали иной смысл. Происходит он от древнегреческого слова mechane, которым называли все искусно придуманное, понимая при этом механическое искусство. Это относилось как к различным машинам и механизмам, так и вообще к «хитроумным» изобретениям. Слово mechane употреблялось и в более узком смысле. Первоначально оно обозначало название подъемных машин, в частности машин, с помощью которых в греческих театрах поднимали и опускали актеров, и вообще механизмов, позволяющих посредством силы поднимать значительные тяжести на достаточно большую высоту.

Позже этим словом стали называть различные метательные машины, применявшиеся в античной технике.

В настоящее время теория машин и механизмов является одним из разделов механики, а название «механика» распространено на науку о всех видах механического движения.

Простейшее определение науки можно сформулировать так: наука есть систематическое собрание теоретических положений и практических методов исследования заданного предмета или совокупности предметов. Отсюда следует, что изложение истории науки можно начинать с появления письменных трактатов, касающихся этой науки. Однако могут быть и исключения: например, основные сочинения по религии и философии индийцев долгое время передавались устно без какой-либо записи; то же самое наблюдалось и в Европе, где священные книги галльских друидов выучивались наизусть, вследствие чего полная система их религиозных и философских представлений осталась неизвестной; однако эти исключения лишь подтверждают правило.

В этом отношении история науки отличается от истории техники, в которой материальные памятники имеют доминирующее значение. Можно изучать технику Древнего Египта, Вавилона, даже технику эпохи палеолита, но для изучения истории науки решающую роль играют письменные памятники.

Историю механики как науки о машинах и механизмах можно начинать с очень глубокой древности. Уже в эпоху неолита и бронзового века появилось колесо, несколько позже применяются рычаг и наклонная плоскость. Регулярное применение рычага и наклонной плоскости начинается в связи со строительными работами в древневосточных государствах. И, разумеется, все это время шел процесс выработки, осознания ряда более или менее абстрактных понятий, таких, как сила, сопротивление, перемещение, скорость.

Народы, создавшие великие цивилизации в бассейнах Нила, Тигра и Евфрата, были хорошо знакомы с такими механическими орудиями, как рычаг и клин. Первые египетские пирамиды строились примерно за три тысячи лет до нашей эры. На сооружение самой высокой из них – пирамиды фараона Хуфу (Хеопса) пошло 23 300 000 каменных глыб, средний вес которых равен 2,5 т. При сооружении храмов, колоссальных статуй и обелисков вес отдельных глыб достигал десятков и даже сотен тонн. Такие глыбы из каменоломен доставлялись на место сооружения храма на специальных салазках. В каменоломнях для отрыва каменных глыб от породы служил клин. Подъем тяжестей осуществлялся с помощью наклонной плоскости. Например, наклонная дорога к пирамиде Хафра (Хефрена) имела подъем 45,8 м и длину 494,6 м. Следовательно, угол наклона к горизонту составлял около 5,3°, и выигрыш в силе при поднятии тяжестей на эту высоту был значительным. Для облицовки и пригонки камней, а возможно, и при подъеме их со ступеньки на ступеньку применялись качалки. Для поднятия и горизонтального перемещения каменных глыб служил также рычаг. С древнейших времен был известен в Египте и рычаг для подъема воды (шадуф).

Ирригационные сооружения междуречья Тигра и Евфрата (Древний Вавилон), Средней Азии (Древний Хорезм, Согдиана) и Ирана, высокий уровень строительной техники, о котором свидетельствуют многочисленные памятники этой эпохи, позволяют предположить, что при их постройке также использовались «простые машины»: рычаг, клип, наклонная плоскость. С давнего времени (и почти до наших дней) в ирригационных сооружениях Средней Азии для подъема воды служил чигирь – усовершенствованный вариант египетского шадуфа.

Однако до нас не дошел ни один древнеегипетский или вавилонский текст с описанием действия подобных машин. Поэтому остается открытым вопрос, были ли известны тогда, например, свойства рычага, которые греки позднее выразили при помощи пропорций, ныне знакомых каждому школьнику. То же относится к древней Средней Азии и Ирану, где письменные источники практически не сохранились: найдены лишь небольшие фрагменты древнехорезмийских и согдийских рукописей. Основная масса их была уничтожена во время арабского завоевания Средней Азии в VIII в. н. э.

Таким образом, механику Древнего Востока можно отнести к предыстории современной механики. Этот период предыстории характеризуется применением результатов накопленного практического опыта, и эти результаты, видимо, не подвергались теоретической обработке.

Известно, однако, что некоторой теоретической обработке в Древнем Вавилоне подвергались результаты астрономических наблюдений. С точки зрения истории механики значительный интерес представляют вавилонские методы вычисления параметров движения небесных тел, которые реконструированы, правда, на основании изучения вавилонских астрономических текстов достаточно поздней эпохи – эпохи Селевкидов (III – I вв. до н. э.). Это таблицы эфемерид Солнца, Луны и планет, содержащие константы периодического движения светил.

Так как наблюдательные инструменты вавилонян не могли гарантировать точность даже в секундах, а данные таблиц имеют точность до терций, естественно предположить, что вавилонские астрономы обрабатывали результаты наблюдений таким образом, чтобы представить их в виде арифметических рядов, соответствующих ступенчатой и линейной зигзагообразной функциям. На таком уровне научного мышления представление о скорости движения должно было принять достаточно абстрактный характер.

Характер античной механики определялся экономическими основами рабовладельческого хозяйства. Развитие рабства в Греции явилось предпосылкой для более широкого разделения труда в производстве. До известного периода это обеспечивало более быстрый рост техники и производительных сил, рабовладельцы же получили досуг для интеллектуальной деятельности. Однако рабовладельческое хозяйство содержало в себе элементы, тормозившие дальнейший рост техники. Рабам в основном поручались такие примитивные работы, которые или вообще не требовали орудий труда, или выполнялись крайне грубыми орудиями, так как раб, низведенный сам до степени орудия труда, не был заинтересован пи в сохранности, ни в совершенствовании этих орудий.

Таким образом, из особенностей рабовладельческой экономики вытекали примитивный характер античной техники и ее медленная эволюция. К рычагу и клину в эллинистическую эпоху, начавшуюся на рубеже IV – III вв. до п. э., добавляются еще блок и винт. В виноделии и маслоделии использовался пресс, как рычажный, так и основанный на принципе вдавливаемого клина, а затем винтовой. Для подъема и горизонтального передвижения тяжестей греки и римляне применяли ворот – с горизонтальной осью в первом случае и с вертикальной – во втором. В строительном деле употреблялись также блоки и системы блоков – полиспасты. Вращательные движения преобразовывали с помощью систем зубчатых колес. Более сложные механические орудия (водяное колесо, червячная передача, винт, насос, и т. д.) применялись сравнительно редко – рабский труд препятствовал распространению механических приспособлений.

Однако в античном мире были виды деятельности, не связанные или почти не связанные с применением рабского труда. Это – военное и морское дело, потребностями которых в значительной степени определялось развитие античной техники. На греческих и римских судах, как гражданских, так и военных, рабы использовались лишь в качестве гребцов. Более ответственные операции – управление рулями, парусами и т. д. – были делом свободных граждан.

Уровень развития техники в военном деле (особенно в эллинистический и римский периоды) был значительно выше, чем в сельском хозяйстве. Уже в V в. до н. э. (Пелопонесская война) в афинской армии применялись тараны, которые достигали гигантских размеров. Для метания больших стрел пользовались катапультами; прототипом пулемета был полибол для непрерывного метания стрел; баллисты служили для метания камней. С их помощью ядро в 4 фунта могло быть брошено на расстояние до 300 м. Существовали специальные прицельные приспособления и приборы для изменения траектории.

Очень важным видом деятельности, способствующим развитию техники и механических приспособлений, явилось ремесленное производство, которое (особенно в Греции и эллинистическом мире) было в значительной степени уделом свободных граждан. Именно с ремесленным производством связана разработка различных способов поднятия и перемещения тяжестей при помощи механических приспособлений, «хитроумных устройств», в ткацком, гончарном, ювелирном деле и т. д., т. е. всего того, что, пользуясь современной терминологией, можно объединить в понятие «техническая механика».

Значительным стимулом совершенствования механических устройств было развитие торговли (как внутренней, так главным образом и международной), связанной с применением золота в качестве менового эквивалента и распространением драгоценных камней. Это способствовало использованию рычага в различных его видах, так как торговые операции требовали более точных способов взвешивания. Появляются весы и безмены самых разнообразных конструкций: с перемещающейся точкой опоры, с неподвижной точкой опоры, но перемещающимся грузом и т. д. Практика взвешивания грузов на безменах основывалась на эмпирическом знании закона рычага, и сама она в свою очередь доводила эти законы до степени очевидности. Устройство безмена было основано на твердом убеждении, что двойному грузу, подвешенному к одному плечу рычага (с неподвижной точкой опоры и постоянным по величине противовесом), соответствует вдвое большее удаление противовеса от точки опоры.

Следует признать, что теоретическая механика начала развиваться в Греции. Теоретическая механика возникла в Греции в V в. до н.э. одновременно с появлением в театре греческой трагедии Эсхилла, Софокла и Еврипида. На первый взгляд может показаться странным, что такая строгая наука получила свое начало в театре; нужно, однако, отметить, что это произошло не только с механикой: другая, не менее строгая наука – оптика – родилась тоже в театре в связи с необходимостью писать декорации требовалась теория перспективы.

Объяснить это можно тем, что основой античной культуры было рабовладение; в Риме рабский труд применялся в сельском хозяйстве (в больших фермах – латифундиях), а в Греции – в промышленности; рабы работали в мастерских. Изобретать машины для увеличения производительности труда не было смысла: рабам давали самые грубые и дешевые инструменты, а повышение производительности труда достигалось при помощи других мер.

Немного позже слово mechan получило и другое значение: так стали называться военные машины. В дальнейшем после возникновения Римской империи слово mechan, или machine, стало употребляться для обозначения всякого производственного приспособления, где при помощи малой силы требовалось получить большую.

Здесь имеется характерное отличие античной техники от современной. В настоящее время используются мощности в десятки тысяч лошадиных сил, но при этом экономятся материалы, мировые запасы полезных ископаемых подсчитаны.

В Греции положение было обратным: двигателями были люди и животные, наибольшей мощностью была одна слоновья сила, да и то слоны применялись только в военном деле; зато материала греки имели для своих потребностей вполне достаточно.

Принципиально новым для античной механики по сравнению с научными достижениями Древнего Востока было то, что наряду со стихийным применением результатов многовекового практического опыта появляются и механические теории.

Характерной чертой античной механики является разобщенность учения о движении – кинематики и учения о равновесии – статики. Развитие этих основные областей механики в течение длительного времени (вплоть до XVII в. – периода объединения их в единую науку) шло независимо друг от друга. И это в значительной мере предопределено традициями античной науки. Учение о движении разрабатывалось в рамках общего учения о природе: вопрос о сущности движения был одной из фундаментальных проблем древнегреческой философии. Чисто кинематическое описание движений стало делом астрономов, создававших и достаточно сложные инструменты для своих наблюдений и измерений, и механические модели мироздания: движение небесных тел, согласно общепринятым в античной науке взглядам, не требовало причинных объяснений. Учение о равновесии развивалось на основе опыта применения различных приспособлений.

Таким образом, есть основание выделить три направления и три линии развития в теоретической механике античного мира, которая зародилась в Древней Греции в VI – V вв. до н. э. и развивалась затем в эллинистических государствах и в созданной римлянами империи примерно до V в. н. э. Статика была почти непосредственно связана с техническими запросами; ее основными проблемами был расчет выигрыша в силе, достижимого с помощью известных механических приспособлений, и вывод условий равновесия при взвешивании и плавании тел. Кинематическое направление находилось, по крайней мере в эллинистическую эпоху, в русле астрономической традиции, к тому времени имевшей многовековую историю. В обеих этих областях был достигнут достаточно высокий уровень математизации этой науки – с использованием геометрии, тригонометрии и методов инфинитезимального характера. Общее учение о движении, чем занимались философы, было в основном качественной теорией. Оно в соответствии с установками главных философских школ эпохи оставляло в стороне количественную сторону дела и искало объяснения механических явлений, опираясь на повседневный опыт и наблюдения, путем сравнений и сопоставлений.

О греческой динамике можно составить полное представление из следующих сочинений Аристотеля (374-322 гг. до н.э.): «Физика», «О небе», «О возникновении и уничтожении», «О метеорах» и отчасти «Метафизика». Что касается так называемых «Механических проблем», то они вышли из аристотелевской школы, но вряд ли они принадлежат самому Аристотелю.

Аристотель под движением (kinesis) понимал изменение вообще, различая количественные и качественные изменения, а также изменения в отношении места, которые составляют то, что теперь называют механическими движениями. Кроме этого, Аристотель называл движением переход из одного состояния в другое, например «из бытия в небытие», из здоровья в болезнь и обратно. Эта направленность из чего-нибудь во что-нибудь – определение начала и конца цели – была характерной для философии Аристотеля.

Для нас существенным является направление движения, для греков же – начальная и конечная точки. Это относится не только к философии: в греческой геометрии прямой называется то, что сейчас определяется как отрезок. Греки понимали, что такое бесконечность, но пользоваться ею избегали.

В механике определение движения по начальной и конечным точкам приводило к некоторым неудобствам: круговое движение Аристотель определял как движение из чего-нибудь в то же самое и специально подчеркивал, что круговое движение едино. Поэтому механики-практики, например Герон, рассматривая движение зубчатых колес, прибегали к таким описательным выражениям: колесо, в котором верхняя половина движется слева направо, а нижняя справа налево, и т.д.

В астрономии различались движения: в направлении последовательности знаков зодиака (видимое движение планет по небесному своду) и против последовательности знаков (суточное вращение неба, объясняющее восход и заход светил). Но небо у греков было резко отделено от Земли; нижний, подлунный мир был местом возникающего и уничтожающегося, подверженного переменам, тогда как верхний надлунный мир был вечным, совершенным и неизменяемым. Различие между обоими мирами замечалось и в характере движений.

Греки различали два вида движений: естественные и насильственные. Естественные движения происходили сами собой без вмешательства посторонней силы (их можно назвать инерционными); насильственные же движения требовали некоторого двигателя. Естественные движения представляли стремления тел занять свое «естественное место»; для тяжелых тел таким местом была Земля; выпущенный из рук камень падал вниз сам по себе, а для сообщения ему движения вверх надо было приложить какую-то силу.

С другой стороны, огонь, например, обладал естественным движением вверх, а чтобы сбить его вниз, нужно было приложить некоторые усилия. Это естественное стремление получило название ϱοπ (корень ), а выражающий это движение глагол (в неопределенной форме ) – рыпаться; по-польски ruch – движение (одинаковый корень со словом «рушиться»). Так как в подлунном мире все является преходящим, то и естественные движения должны были иметь начало и конец – быть прямолинейными. В надлунном же мире, где все является вечным и неизменным, должны быть вечными и естественные движения, иными словам, они должны быть равномерными и круговыми.

Понятие ϱοπ соответствует нашему понятию об инерции, или силе инерции, в том смысле, как ее понимал Ньютон, а также большинство людей, не очень знакомых с теоретической механикой. Однако современные понятия об инерции значительно отличаются от тех, которые имелись у древних греков. Для нас понятие об инерции тесно связывается с прямолинейным и равномерным движением; когда движущееся равномерно тело встречает препятствие, то инерция уступает место подействовавшим на тело силам. У греков же, наоборот, ϱοπ начинало проявлять себя именно, когда движущееся тело встречало препятствие. Если какая-либо точка тела оказывалась неподвижной, то инерция остальных точек заставляла их продолжать свое движение, иными словами, вращаться вокруг неподвижной точки.

Таким образом, ϱοπ проявлялась в виде вращающего момента. Если ϱοπ различных точек взаимно нейтрализовывались, то тело останавливалось; наступало состояние, которое теперь называют равновесие, а греки называли ισοϱϱοπια, что можно перевести как равномоментность.

В настоящее время закрепленную точку, вызывающую равновесие, называют центром тяжести и рассматривают как точку приложения равнодействующей всех сил тяжести отдельных точек тела; греки называли ее ϰέντϱον ϱοπης (центром моментов); название ϰέντϱον του βάϱος (центр тяжести) появилось позднее, так как ϱοπή считалась пропорциональной весу тела. Центр тяжести у греков определялся как точка, при закреплении которой тело оставалось неподвижным во всяких положениях.

Дальнейшей задачей исследования было определение величины ϱοπή численно. Греки в своих теоретических исследованиях шли несколько иным путем: они говорили не о числовом значении, а о равенстве, или пропорциональности, двух значений одной и той же величины. Для ϱοπή эта задача была решена Архимедом, который показал, что ϱοπή двух материальных точек весом Р и Q одинаковы, если их расстояния а и b до закрепленной точки обратно пропорциональны соответствующим весам:

На практике это равенство давало условие равновесия рычага.

Следующей задачей, которую поставил и для отдельных случаев решил Архимед, было определение центра моментов, или тяжести, плоских фигур. Совокупность этих исследований дала прочную базу для исследования работы машин, основанных на принципе рычага (воротов, блоков, полиспастов и т. д.), но не могла решить вопроса относительно работы машин, основанных на принципе наклонной плоскости (клин, винт и т. п.). Эта задача была решена значительно позже, в XIII в., и уже на основании других принципов, которые были связаны с другим понятием о силе, а именно о силе, производящей насильственные движения.

Эту силу Аристотель назвал δύναμις (dynamis) и определил ее так. Если А —движущее, В — движимое, Г — длина, на которую оно продвинуто, Δ — время, в течение которого оно двигалось, то в такое же время сила, равная A, продвинет половину В на двойную длину Г, а на целую Г — в половину времени Δ; такова пропорция. Кроме того, считалось, что «двигатель» и «движимое» находились в непосредственном соприкосновении.

В современных терминах формулу Аристотеля можно выразить так:

где F — (у Аристотеля А) — сила, Р — вес движимого тела, L и Т — длина и время движения, k — отсутствующий у Аристотеля коэффициент пропорциональности.

Строго говоря, у Аристотеля величину Р можно понимать и как сопротивление, но поскольку реальными сопротивлениями были вес поднимаемого тела или пропорциональная весу сила трения, то при наличии коэффициента пропорциональности k можно полагать величину В равной весу Р.

Если обратить взимание на размерность величин, входящих в формулу Аристотеля, то станет ясным, что его понятие dynamis имеет размерность мощности. Это станет очевидным, если учесть, что греческое слово dynamis переводится латинским potentia, которое в свою очередь соответствует французскому puissance, т. е. мощности.

Определение Аристотеля вполне соответствовало уровню техники, когда движущая сила получалась от живых двигателей — рабов или животных. Для перевозки вдвое более тяжелого груза или для

получения вдвое большей скорости требовалось и двойное количество животных. Такое понимание до сих пор соответствует термину «лошадиная сила».

Однако в определении Аристотеля имелся очень большой недостаток. Если отношение пройденной длины L ко времени Т заменить измеряемой этим отношением скоростью v, то формула Аристотеля примет вид

Очевидно, что если F = 0, то и v = 0, и обратно. Но не всегда при v, не равном нулю, F = 0. Были явления, которые заставляли Аристотеля задумываться над тем, какая сила заставляет двигаться стрелу; выпущенную из лука? В этом случае еще можно было предположить, что спущенная тетива возмущает воздух, который потом и несет стрелу (так называемая теория антиперистасиса), но «кабинетность» этого объяснения чувствовалась очень сильно. Можно даже сказать, что, когда Аристотель писал свою формулу, она уже не соответствовала действительному положению вещей.

Что же было основной причиной этого изменения? Ее следует искать, конечно, не в каком-нибудь промышленном перевороте, маловероятном в рабовладельческом обществе; он произошел совсем в другой области, а именно в военном деле.

Положение Греции в пору ее наибольшего расцвета — в середине V в. До н. э. — достаточно хорошо известно. В 431 г. началась описанная Фукидидом Пелопоннесская война, сыгравшая в истории Греции очень важную роль. Греческие войска в ту эпоху составлялись из граждан, которые должны были вооружаться и кормиться за свой счет. Походы не были особенно продолжительными, а самое главное —греки не очень умели брать города.

В ходе этой войны Афины решили завоевать Сицилию, но их поход (415—413 гг. до н. э.) оказался неудачным; главный город Сицилии Сиракузы отстоял свою свободу. Через четыре года после отражения афинян Сицилии стала грозить опасность с другой стороны — от карфагенян. Карфаген представлял государство другой типа, обладавшее развитой промышленностью.

В 409 г. до н. э. в Сицилии высадился карфагенский полководец Ганнибал, использовав большое количество кораблей, на которых доставлялись осадные машины, стрелы и другие запасы. Благодаря, применению техники он разрушил и завоевал многие сицилийские города.

В 405 г. до н. э. в Сиракузах Дионисий Старший начинает готовиться к войне. Во время этой подготовки он объявляет первую в мировой истории мобилизацию промышленности. Он собрал техников (τεχνίταζ) из подчиненных ему городов, из Италии и Греции, из мест, подчиненных Карфагену, привлекая их большим жалованьем. Зная, что война будет тяжелой и продолжительной, он задумал приготовить в изобилии вооружения и разнообразные метательные орудия и, кроме того, корабли с четырьмя и пятью рядами весел (тетреры и пентеры), которые в то время еще не были в употреблении.

Стандартным судном в Греции V в. до н. э. была триера (у римлян — трирема) — судно с тремя рядами весел.

В то время было открыто искусство строить катапульты в Сиракузах, где были собраны сильные инженеры. Они изобрели многие виды метательных машин и новых орудий.

В 397 г. Дионисий снова начал войну с карфагенянами. Ему удалось остановить успехи карфагенян, но полностью изгнать их из Сицилии он не смог: карфагеняне оставались на западе острова еще около полутораста лет.

После этого новые изобретения перешли и в Восточную Грецию; следующий, IV век до н. э. был временем наемных войск и совершенствования военной техники. Особенного расцвета эта техника достигла в войсках Филиппа и Александра Македонских. Учитель Александра Македонского — Аристотель ничего не писал о военной технике. В науке он был биологом, естественником; в математике он разбирался достаточно хорошо (его логические сочинения воспроизводят в большой степени методику греческих математиков того времени), но творческим математиком он не был.

Но можно назвать одного человека, который был и математиком, и инженером, и мог иметь некоторое отношение по крайней мере к теоретической разработке новой техники. Он был автором первого, хотя и не дошедшего до нас, труда по механике. Это был Архит Тарентский, живший примерно около 400 года, пифагореец и друг Платона. Он решил знаменитую делийскую задачу об удвоении куба при помощи необыкновенно остроумного стереометрического построения.

Птолемей называл его крупнейшим пифагорейским теоретиком музыки. Он размышлял также относительно взаимной связи наук и физической природы звука. Он был первым, кто дал систематическую разработку механики на математических основаниях. Согласно Витрувию (автору труда «Об архитектуре») он писал о машинах и даже сам строил машины.

Для истории теоретической механики особенно интересно решение задачи об удвоении куба. Первоначально эта задача была чисто математической и появилась, когда встал вопрос об измерении величин. Естественный ход таков: определенная величина берется за единицу, затем строится другая, которая была бы в два раза больше первой, дальше получаются величины соответственно в три, четыре и т. д. раз больше, что позволяет построить шкалу для натурального ряда величин. Для длин это производится без затруднений, но при измерении площадей после выбора квадрата, площадь которого принималась за единицу, следовало построить квадрат вдвое большей площадью. Эта задача была решена пифагорейцами при помощи средней пропорциональной: если сторона квадрата единичной площадью равна а, то сторона искомого квадрата получится из пропорции:

откуда

и

Это привело к открытию несоизмеримости .

Следующая стадия — измерение объемов — требовала умения построить куб, объем которого был бы в два раза больше объема куба, принятого за единицу. Гиппократ Хиосский (середина V в.) показал, что эта задача может быть решена при помощи двух средних пропорциональных:

но практически задача оставалась нерешенной.

Значение ее Эратосфен характеризует так, что после ее решения можно вообще любой заданный объем, ограниченный прямоугольниками, превращать в куб, одну форму преобразовывать в другую, делать подобной и увеличивать, сохраняя подобие. Это изобретение будет полезно и для желающих увеличить размеры катапульт и камнеметов, так как для увеличения длины броска нужно пропорционально увеличить все: и ширину, и величину отверстия, и втулки, и вставляемые тяжи, а этого нельзя сделать без нахождения средних пропорциональных.

Теперь известно, что для увеличения вдвое дальности полета снаряда в движении по параболической траектории нужно вдвое увеличить его начальную кинетическую энергию, а так как потенциальная энергия упругого тела при одинаковых напряжениях пропорциональна его объему, то для указанной цели требовалось удвоение объема тяжа.

Решение, данное Архитом, представляет большой интерес и с точки зрения механики; можно сказать, что Архит был одним из первых, кто ввел движение в решение геометрических задач.

Практическое выполнение его построения представляло затруднения; поэтому в дальнейшем многие математики занимались нахождением более удобных решений; одно из них приведено в «Механике» (а также в «Баллистике») Герона Александрийского, что еще раз показывает важность этой задачи и для механики.

Оказалось непригодным и данное Аристотелем определение силы как мощности, так как рассуждение о полете стрелы, поддерживаемой воздухом, никак не могло годиться к объяснению полета камня, выброшенного из катапульты.

Новое определение силы в эллинистическую эпоху (II—I вв. до н. э.) можно восстановить только по цитатам. В частности, оно имелось в сочинениях комментатора Аристотеля Александра Афродизского (около 200 г. н. э.), который заимствовал его у знаменитого астронома Гиппарха (около 150 г., до н. э.). Александр Афродизский был известен Галилею, который упоминает об этом определении в своем юношеском сочинении «О движении».

Согласно этому определению движущееся тело в момент начала движения получает некоторую движущую силу, которая и поддерживает движение (итальянские механики конца средневековья называли эту силу impeto — импульс); когда эта сила иссякает, то движение прекращается.

Эллинистическое определение силы соответствует термину «живая сила», или «работа». Из аристотелевской формулы новое определение получается, если зачеркнуть время Т в знаменателе. Тогда определение силы будет иметь вид

Такое определение силы было и у Декарта, который измерял силу произведением веса поднимаемого тела на высоту его поднятия.

Из простейших машин греки хорошо знали лишь теорию действия рычага, которая и составляет основное содержание приписываемых Аристотелю «Механических проблем». Данное в этом произведении доказательство закона рычага содержит некоторые моменты, очень важные для дальнейшего развития механики.

Основную причину действия рычага автор «Механических проблем» находит в том, что во вращении точки; более удаленные от оси, движутся быстрее, чем точки, менее удаленные (§1).

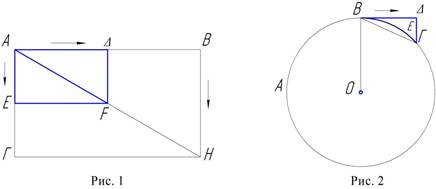
Причиной этих явлений является то, что описывающая круг точка участвует в двух перемещениях. Если бы эти перемещения находились в каком-нибудь отношении, то движущаяся точка пошла бы по прямой, и эта прямая будет диагональю фигуры, образованной двумя составленными вместе прямыми, находящимися в том же отношении (рис. 1).

Пусть отношение прямых, по которым перемещается движущаяся точка, будет такое, какое АВ имеет к АГ, и пусть прямая АГ движется к точке В, а линия АВ переносится к НГ пусть точка А дойдет до Δ, а линия АВ до Е (EF). Если перемещения имеют отношение, как у линий АВ и АГ, то необходимо, чтобы то же самое отношение имели бы и отрезки AΔ и АЕ. Следовательно, малый параллелограмм подобен большому и оба они имеют одну и ту же диагональ, а точка А окажется в H.

Такое же доказательство можно привести и для случая, когда движение прекратится в любой другой точке; точка А все время будет находиться на диагонали.

Выше приведено доказательство параллелограмма перемещений; если скорость равномерного движения равна пути, пройденному в определенное время, то можно считать, что имеется параллелограмм скоростей.

Древние греки знали параллелограмм скоростей по крайней мере для прямолинейных равномерных движений. Как указывается в «Механических проблемах», если бы точка имела два перемещения, ни в какое время не находящихся ни в каком отношении (иными словами, несоизмеримые), то невозможно, чтобы окончательное перемещение было прямолинейным.

Действительно, пусть перемещение будет прямолинейным. Тогда, если взять его как диагональ и дополнить стороны, то движущаяся точка будет перемещаться в отношении сторон, ибо это уже доказано ранее. Следовательно, движение, не находящееся ни в каком отношении, ни в какое время не произведет прямой. Действительно, если бы точка в течение некоторого времени двигалась в некотором отношении, то согласно вышесказанному ее перемещение было бы прямолинейным. Таким образом, если два перемещения не находятся ни в какое время ни в каком отношении, то движущаяся точка окажется перемещающейся криволинейно.

Из этого ясно, что точка, описывающая круг, имеет одновременно два перемещения и что, двигаясь по прямой, она попадает на перпендикуляр, так что эта прямая окажется перпендикулярной к радиусу. Пусть будет (рис. 2) круг АВГ и пусть точка В движется к Δ; по кругу она когда-нибудь достигнет точки Г. Если бы она перемещалась в отношении ВΔ к ΔГ, то она двигалась бы по диагонали ВГ. Поскольку между ВΔ и ΔГ никакого отношения нет, то она будет перемещаться по дуге ВЕГ. Совершенно очевидно, что перемещения отрезков ВΔ и ВГ никак не могут быть соизмеримыми, иначе движение происходило бы по хорде ВГ; в действительности же движение происходит по дуге ВЕГ.

Если отрезок ВΔ будет бесконечно малым первого порядка, то ΔГ окажется бесконечно малым второго порядка, так что указанные отрезки являются несоизмеримыми. Можно отказаться от предположения о бесконечной малости; в таком случае разговор может идти о так называемых неархимедовых величинах, классическим примером которых являются криволинейные углы, т. е. углы, заключенные между прямой и окружностью, в частности между окружностью и касательной к ней.

Следы употребления криволинейных углов имеются у Евклида (определение «угла сегмента» в книге III «Начал»). В дальнейшем развитии греческой геометрии углы между прямой и окружностью были отброшены, по всей вероятности, именно по той причине, что являлись «неархимедовыми» величинами, несоизмеримыми с прямолинейными углами.

Отметим, что схема (рис. 2) была исходной для Гюйгенса, когда он выводил формулу, приведшую к определению нормального ускорения.

Наиболее ранние сочинения античных авторов, содержащие механические теории, не сохранились. Однако несомненно, что большинство этих теорий посвящено проблемам статики и что их основой служил принцип рычага. Известно, что Архит Тарентский (ок. 428 – 365 г. до н. э.) разрабатывал теорию блока полиспастов, но результаты его исследований до нас не дошли. Ему же некоторые античные авторы приписывают изобретение винта. Изобретение бесконечного винта для подъема и передвижения тяжестей и бесконечного водоподъемного винта связывают с именем Архимеда. По-видимому, появление винта вызвало постановку новых технических и математических проблем. Однако, если следовать хронологии источников, надо начинать не с Архимеда, а с философов Древней Греции.

Уже на ранних стадиях развития греческой философии можно обнаружить зачатки двух принципиально различных механических концепций, которые можно назвать кинетической и динамической.

Основные положения динамической концепции древних сводились к следующему: материи чуждо самодвижение – сама по себе она может пребывать лишь в покое; движение материи определяется действием на нее активных движущих начал – сил, существующих независимо от нее и действующих извне. По Эмпедоклу, например, материя приводится в движение двумя противоборствующими мировыми силами: любовью и враждой.

Напротив, с точки зрения кинетической концепции в природе нет каких-либо особых начал движения, не связанных с материей: материи свойственно самодвижение. Наиболее последовательными представителями античного кинетизма были атомисты – Левкипп, Демокрит, Эпикур и Лукреций. Принцип механического самодвижения материи в общей форме выражен в их учении о несоздаваемости и неразрушимости материи и движения. Согласно атомистам, природа ничего не содержит, кроме материи, движущейся в пустом пространстве.

Яркое и определенное выражение идея вечности и неуничтожаемости движения нашла у Гераклита Эфесского (ок. 530 г. – ок. 470 г. до н. э.). Гераклит учил, что все существующее в природе возникает из вечно движущегося огня. Огонь Гераклита нужно понимать не в смысле обычного пламени, но как некую огнеподобную первооснову вещей. Мир как совокупность вещей сотворен не богом или человеком, а был, есть и будет вечно живым огнем, закономерно воспламеняющимся и закономерно угасающим. Об этом фрагменте Ленин замечает: «Очень хорошее изложение начал диалектического материализма».

Учение о вечности движения вызвало реакцию со стороны Парменида и других философов элейской школы, которые считали, что это учение делает невозможным познание, ибо о там, что меняется, нельзя сказать ничего определенного. Элеаты утверждали, что истинное бытие неподвижно и находится вне времени и пространства, а наши представления о пространстве, времени и движении противоречивы и сложны. Это положение защищалось мастером древней диалектики Зеноном в его знаменитых «Парадоксах». Наибольшее же влияние на дальнейшее развитие механики оказало учение Аристотеля.

В аристотелевской натурфилософии фундаментальное место занимает учение о движении. Его сочинения «Физика», «О небе», «О возникновении и уничтожении», «О метеорах» и отчасти «Метафизика» содержит достаточно полное изложение общих понятий механики.

Движение он понимает в широком смысле, как изменение вообще, различая изменения качественные, количественные и изменения в пространстве.

Кроме того, в понятие движения он включает психологические и социальные изменения – там, где речь идет об усвоении человеком технических знаний или об обработке материалов. Понятие движения включает в себя также переход из одного состояния в другое, например из бытия в небытие. Механическое движение, т. е. изменение в пространстве, Аристотель рассматривает, таким образом, как частный случай движения вообще.

Не удовлетворяясь учением о механической причинности, развивающимся древними атомистами, Аристотель различал четыре вида причин: материальную, действующую (или причину движения), формальную pi финальную (цель, или «ради чего»). В первой книге «Метафизики» Аристотель отмечает, что до него ученые указывали на материальную причину (ионийские натурфилософы), затем добавили причину движения (элеаты, Эмпедокл и Анаксагор) и, наконец, некоторые говорили о формальных причинах, признавая идеи за начала вещей (школа Платона), но лишь он впервые указал на цель (или «ради чего») как на четвертую причину образования вещей. Эти телеологические моменты физического учения Аристотеля впоследствии были раздуты средневековой схоластикой.

На основе различения четырех причин Аристотель ставит вопрос об источнике движения. Материя сама по себе является пассивным началом и низшим по отношению к форме: ей чуждо самодвижение. Согласно учению атомистов, в пустоте тела могут сохранять наличное движение само по себе, без внешних импульсов. Напротив, в учении Аристотеля центральным пунктом является идея косности, пассивности материи. На первый план выдвигается различие между движимым и движущим. Даже в самодвижущихся одушевленных телах Аристотель различал движимое и движущее. Они также требуют наличия чего-то движущего; разница лишь в том, что неодушевленные тела имеют источник движения вовне, в то время как самодвижущееся тело имеет такой источник в самом себе. Аристотель выделяет движения прямолинейные, или ограниченные, и круговые, или неограниченные. Круговое движение, которое он считает «совершенным», свойственно небесным телам. Далее Аристотель различает два вида движений: «естественное» и «насильственное». «Естественные» движения совершаются сами собой, без всякого вмешательства извне. «Насильственные» движения для своего осуществления требуют такого вмешательства.

Для объяснения причины «естественного движения», не связанного с движением небесных тел (Вообще движения тел в земных условиях получило название местного), Аристотель вводит понятие «естественного места». Стремление к «естественному месту» заложено в каждом теле, совершающем «естественное движение». Каждому роду тел свойственно свое «естественное место»: для тяжелых тел это Земля, поэтому они на нее падают, а для легких – огонь, т. е. расположенная над воздухом огненная сфера, поэтому они поднимаются вверх. Если какое-либо тело переместить из его «естественного места», оно будет стремиться назад, совершая прямолинейное движение. Небесным телам свойственно стремление к «совершенному» круговому движению.

Для «естественных» движений это нечто, присущее самому телу, а для «насильственных» - внешняя причина движения.

Под силой Аристотель понимает всякую способность, поскольку последняя может быть причиной начала действия или противодействия. «Движущая сила» в «насильственном движении» зависит от «активности» источника движения, т. е. от степени приложенной к движущемуся телу мускульной энергии человека или животного.

Сила для Аристотеля – причина движения, и она должна непрерывно поддерживать движение (В силу логического принципа, «с прекращением причины прекращается ее действие». При этом под прекращением действия понималось и исчезновение результата предыдущего действия причины). Но тогда возникает вопрос: чем же поддерживается движение в телах, оторвавшихся от того, что их двигало, т. е. силы, которая сообщила им движение? Аристотель отмечает, что когда мы толкаем по плоскости тело, например шар на столе, то одновременно приводим в движение и окружающий его воздух. В образующуюся за движущимся шаром пустоту устремляется воздух и как бы подталкивает его. По этой причине шар не останавливается мгновенно после прекращения действия силы, а некоторое время движется вследствие воздействия окружающей среды. Воздушная среда в данном случае является активным началом движения, ибо, не будь ее, тело должно было бы мгновенно прийти в состояние покоя.

В отличие от элеатов Аристотель считает движение вечным. «Невозможно допустить, чтобы не было движения... Движение необходимо существует всегда». Но он расходится и с древними атомистами: материя не самодвижима. Различая движущее и движимое, Аристотель утверждает, что «одни из существующих предметов неподвижны, другие всегда движутся, третьи причастны к покою и движению».

Предположим теперь, что движение тела А₁ обусловлено движением тела А₂, движение тела А₂ – движением тела А₃ и т. д. Чтобы не продолжать без конца этот процесс, полагал Аристотель, мы должны признать существование первого двигателя, который должен быть либо Неподвижным, либо самодвижущимся. В последнем случае нужно различить в нем движимую и движущую части. А так как двигатель в самодвижущемся теле уже ничем не приводится в движение, то сам он должен быть неподвижным, и, следовательно, если рассматривать цепь, в которой всякое последующее звено представляет движимое, то первое звено этой цепи должно быть извечным «первичным неподвижным двигателем».

Первичный неподвижный двигатель, по Аристотелю, порождает простые, однородные, непрерывные и бесконечные движения. Вращательные движения небесных сфер являются примером таких вечных непрерывных и совершенных движений.

Существование неподвижных вечных двигателей аргументируется также ссылкой на вечность движения: если бы не существовало первых начал движения, неподвижных и вечных по своей природе, то движение не могло бы быть вечным.

Таким образом, вечным у Аристотеля является только вращательное движение небесных сфер, да и оно не мыслится без первого двигателя. В земных же условиях движение (местное движение) происходит по упомянутому уже принципу, ставшему догмой средневековой науки: «с прекращением причины прекращается ее следствие». Поэтому как между движением небесных и земных тел, так и между состояниями движения и покоя проводится строгое разграничение – в полном соответствии, заметим, с данными повседневного, «житейского» опыта и наблюдений.

У Аристотеля мы находим и соображения, дающие основание для количественного определения силы. Для того чтобы лучше разобраться в сути дела, введем некоторые современные термины и обозначения. То, что Аристотель называет движущим, мы будем называть силой и обозначать буквой f. Величину движимого будем называть весом, или сопротивлением движимого тела (Различия между массой и весом в античной физике нет), и обозначим буквой р. Тогда приводимые ниже рассуждения Аристотеля сведутся к следующему: сила пропорциональна произведению скорости тела, к которому она приложена, на его вес, т. е.

где s – пройденный путь, t – соответствующее время, а v – скорость (Надо только иметь в виду, что такая запись недопустима для греческих ученых: то же содержание выражалось с помощью пропорций, т.е. приравниванием отношений только однородных величин).

Текст самого Аристотеля (с использованием только что указанных обозначений) примет такой вид: «В равное время t сила, равная f, продвинет половину р на двойную длину s, а на целое s в половину времени t. Такова будет пропорция. И если одна и та же сила движет одно и то же тело в определенное время на определенную длину, а половину – в половинное время, то половинная сила продвинет половину движимого тела и в то же время на равную длину».

Заметим тут же, что в силу соблюдения «принципа однородности» наше определение скорости (средней) v=s:t было чуждым античной науке. Для сравнения скоростей тел сопоставляли либо расстояния, пройденные ими за одинаковое время, либо промежутки времени, за которые пройдено было одинаковое расстояние. Соответственно Аристотель вводит понятие «равноскорого» движения, при котором тело «в равное время движется одинаково». «Равноскорым, - говорил он, - является то, что в равное время продвинулось на равную величину», и «...необходимо более быстрому в равное время двигаться больше, в меньшее время – одинаково».

В «Физике» Аристотеля рассматривается и вопрос о сопротивлении движению (перемещению) со стороны среды, в которой движется тело, и со стороны тела. «Чем бестелеснее среда, через которую происходит движение, чем меньше она показывает сопротивления и чем легче разделима, тем быстрее перемещение».

Условием возможности движения является превосходство силы p над сопротивлением движению r, связанным с телом. Если сила p в определенное время t переместит тело с сопротивлением r на расстояние s, то это не значит, что p/2 продвинет тело с сопротивлением r на 5/2 или что p способна переместить тело с сопротивлением 2r на вдвое меньшее расстояние s/2. При этом может случиться, что никакого движения не произойдет. «Иначе, - замечает Аристотель, - и один человек мог бы двигать судно, если только силу гребцов и длину, на которую они все двигали его, разделить на их число».

Следовательно, заключает он, отношение скоростей становится бесконечно большим, когда сопротивление оказывается равным нулю, а последнее возможно только в пустоте. «Для пустоты не существует никакого пропорционального отношения, в каком она (по своей тонкости) превосходила бы тело, так же как и нуля по отношению к числу». Так как «пустота не стоит ни в каком отношении с наполненной средой, то не существует никакого отношения и между скоростями. «Если через тончайшую среду тело проходит во столько-то времени такую-то длину, то, двигаясь через пустоту, оно превзойдет всякую пропорцию».

Таким образом, всякое движение возможно лишь в наполненном пространстве, так как в пустоте оно происходило бы мгновенно. Поэтому Аристотель отвергает существование пустоты.

Второй аргумент в пользу невозможности пустоты Аристотель выдвигает, обращаясь к изучению падения тел, «естественного» движения, обусловленного стремлением тяжелого тела к своему «естественному месту». Согласно учению Аристотеля, четыре стихии (земля, вода, воздух и огонь) расположены во Вселенной концентрически и таким же образом расположены их «естественные места». Все, за исключением огня, имеет «тяжесть», находясь в своем «естественном месте». Если же вышележащая стихия насильственно перемещена в нижележащую, она проявляет стремление к своему «естественному месту», т. е. приобретает «легкость». Так Аристотель объясняет, почему одни и те же тела (например, дерево) опускаются в воздухе и всплывают в воде. Однако в своих рассуждениях он почти не обращается к рассмотрению движения «легких» тел, а интересуется движением брошенных или падающих «тяжелых» тел, с которым связывает вопросы скорости и ее возрастания. Скорость падения тела в разных средах в силу изложенного выше обратно пропорциональна «тяжести» тела. Аристотель считал, что из двух тел одинакового объема и формы падает в воздухе быстрее то, у которого больше «тяжесть». «Тела, имеющие большую силу тяжести или легкости, если они в остальном имеют одинаковую фигуру, скорее проходят равное пространство в том пропорциональном отношении, в каком указанные величины находятся друг к другу». Различие скоростей падения в материальной среде обусловлено только тем, что более «тяжелые» тела одинакового объема и формы легче «разделяют среду своей силой». Если же рассматривать движение тела в пустоте, то это условие отпадает. Следовательно, в пустоте все тела должны иметь равную скорость, но это невозможно.

В соответствии с этим ни Аристотель, ни его последователи не рассматривали падения тела в пустоте, так как для них пустота является физическим абсурдом. Когда Аристотель говорит о различной скорости падения, он всегда имеет в виду падение в различных средах. Поэтому он отвергает учение атомистов о существовании абсолютно пустого пространства, независимого от находящихся в нем тел и индифферентного ко всякого рода их взаимодействиям. Пространство, понимаемое как чистое протяжение и являющееся пассивным вместилищем тел, несовместимо, по мнению Аристотеля, с понятием движения. Пространство для него – величина, непрерывная по протяженности, а время – величина, непрерывная по последовательности.

Пространство Аристотеля – физическое пространство, свойства и сущность которого связаны с физическим бытием материи. Аристотель определяет «место» не как объем, занимаемый телом в абсолютном, т. е. существующем независимо от тел, пространстве, а как границу объемлющего тела, т. е. тела, соприкасающегося с объемлемым. Место, по Аристотелю, не может быть чем-то принадлежащим предмету. Оно не может быть ни его материей, ни формой, ибо и материя, и форма неотделимы от предмета, в то время как место меняется в процессе движения. О месте в строгом смысле можно говорить лишь при наличии двух тел: объемлющего и объемлемого. Пространство, рассматриваемое как совокупность мест, является наполненным; там, где есть место, должно быть наполненное пространство, ибо место и есть не что иное, как граница объемлющей материальной среды. К пустоте понятие места вообще неприменимо. Земля и небесные тела, отдельно взятые, находятся в известных местах, ибо они окружены мировым эфиром, но мир в целом, сферическая Вселенная античной астрономии, «не находится в месте», так как за пределами этой Вселенной нет больше ничего.

Аргументы атомистов в защиту пустоты Аристотель отводил следующим образом: «Они утверждают, во-первых, что иначе движения по отношению к месту, т. е. перемещения и увеличения, не было бы: нельзя предполагать движения, если не будет пустоты, так как наполненное не имеет возможности воспринять что-либо». «Но нет никакой необходимости, - отвечает Аристотель, если существует движение, признавать пустоту... Это относится только к перемещению, так как тела могут уступать друг другу место одновременно при отсутствии какого-либо отдельного промежутка наряду с ними».

С точки зрения Аристотеля, пустое пространство атомистов является лишь абстракцией чисто геометрических свойств реального физического пространства. Интересно его указание, что если стать па позицию Демокрита, то это с необходимостью повлечет признание неприемлемой для аристотелизма инерции движения. Аристотель пишет: «Никто не может сказать, почему тело, приведенное в движение (в пустоте), где-нибудь остановится, ибо почему оно скорее остановится здесь, а не там. Следовательно, ему необходимо или покоиться, или бесконечно двигаться, если только не помешает что-нибудь сильное». И далее: «Но каким же образом может быть движение по природе, если нет никакого различия в пустоте и в бесконечности; поскольку имеется бесконечность, ничто не будет ни вверху, ни внизу, ни посредине, поскольку пустота – не будет различия между верхом и низом».

Аристотель отвергает учение элеатов об абсолютной неподвижности истинного бытия. «Утверждать, что все покоится, и подыскивать обоснования этому, оставив в стороне свидетельство чувств, будет какой-то немощью мысли и спором... не только против физики, но, так сказать, против всех наук и всех учений, так как все они пользуются движением».

Отвергая существование пустого пространства, Аристотель отвергал и существование «чистого», или «пустого», времени. Вместе с тем он проводил тонкие различия между временем и движением.

Анализируя понятие времени, Аристотель замечает, что некоторые неправильно принимали круговращение неба за само время; в действительности это круговращение служит средством для измерения времени. Если движение не может быть без времени, то и время не существует без движения. «Время не есть движение, но и не существует без движения». Если бы не было изменений, не было бы и времени. При отсутствии изменений все «теперь» были бы тождественны, следовательно, все пребывало бы в едином и нераздельном «теперь». Что же такое время? Так как «мы вместе ощущаем и движение pi время», то «время есть или движение, или нечто, связанное с движением». Но время отлично от движения, так как движения могут иметь различную скорость и, следовательно, они должны измеряться временем. Время же есть «число движений» или «мера движения».

К эпохе античности относится выделение статики в особую теоретическую дисциплину, которую древние называли «искусством взвешивать» и ставили рядом с арифметикой («искусством считать»).

Статика принадлежала к тем естественнонаучным дисциплинам, которые в Древней Греции подвергались наибольшей математизации. Ярким примером этого может служить статика Архимеда, созданная по образцу геометрии Евклида.

К античной эпохе восходит зарождение двух направлений в статике: кинематического и геометрического.

Первое направление, как видно, возникло из практики пользования простыми механизмами (рычагом, наклонной плоскостью и др.) для передвижения и поднятия грузов. При этом законы равновесия тел изучались путем рассмотрения того, что происходит при нарушении равновесия, например, рассматривали неуравновешенный рычаг, т. е. рычаг в движении. Вывод основных теорем статики в этом случае был связан со скрыто или явно принимаемыми допущениями из области динамики.

Второе направление развивалось в связи с расчетом равновесия архитектурных конструкций: балок, плит и т. п., подпертых в одной или нескольких точках, а также равновесия подвешенных тяжелых тел, т. е. всевозможных видов весов (но в таких вопросах использовались и кинематические соображения). При исследовании стремились свести задачу к схеме неподвижного и уравновешенного рычага. С геометрическим направлением статики связано возникновение понятия центра тяжести.

Начало кинематического направления в статике восходит к «Механическим проблемам» псевдо-Аристотеля, геометрическое направление связано прежде всего с именем Архимеда.

«Механические проблемы» - самое давнее дошедшее до нашего времени античное сочинение собственно по механике. Долгое время оно приписывалось Аристотелю. На самом же деле «Механические проблемы» были написаны в начале III в. до н. э. в эллинистическом Египте. На это указывает, например, упоминание о приводящих друг друга в движение бронзовых или железных колесах в святилищах: такие колеса находились в египетских храмах.

Трактат состоит из 36 глав и содержит перечисление и описание ряда механизмов: рычага, колодезного журавля с противовесом, клещей, клина, топора, кривошипа, вала, колеса, катка, полиспаста, гончарного круга, руля и т. д. Не только задачи, но нередко и их решения даются в форме вопросов, т. е. лишь намечаются или даются предположительно.

Центральная тема трактата – принцип рычага, который автор рассматривает как универсальный принцип статики. Поэтому основным содержанием «Проблем» является описание различных видов рычага, к которым сводятся описанные механизмы. Так, например, автор говорит: «Почему два человека, неся одинаковую тяжесть на шесте или на чем-либо подобном, испытывают одинаковую нагрузку только тогда, когда груз находится посредине, и испытывают нагрузку тем большую, чем ближе груз к одному из несущих? Не потому ли, что шест при этих условиях становится рычагом, груз – гипомохлием (точкой опоры) и из носильщиков – тот, кто находится ближе к грузу, становится грузом, приводимым в движение, а второй – грузом, приводящим в движение? Ведь чем дальше этот второй находится от переносимого груза, тем легче он движет и тем более давит книзу на другого, как если бы налегающая тяжесть давила в противоположном направлении и стала гипомохлием. А если груз помещается в середине, то один не оказывается тяжестью для другого и не движет другого, и тот и другой уравновешиваются взаимно». Здесь мы встречаем следующий вопрос: «Почему малый руль, привешенный на корме корабля, имеет столь большую силу?... Быть может, потому, что руль есть рычаг, а рулевой есть то, что приводит его в действие? Стало быть, место, где он прикреплен к кораблю, становится точкой опоры, руль в целом – рычагом, море – грузом, а рулевой – движущей силой».

Попытка более широкого обобщения сделана уже па первой странице сочинения. «Механические проблемы» начинаются словами: «Удивление вызывают из происходящих сообразно природе те явления, причина которых остается неизвестной, а из происходящих вопреки природе те, которые производятся искусством на благо людям... Таковы случаи, когда меньшее одолевает большее и обладающее малой силой приводит в движение большие тяжести, и вообще почти все те проблемы, которые мы называем механическими». И несколько далее: «К затруднениям подобного рода относятся и вопросы о рычаге, ибо кажется несообразным, что большая тяжесть приводится в движение малой силой, и это при еще большей тяжести. Ведь без рычага привести в движение такую тяжесть нельзя, а прибавив тяжесть рычага, можно привести в движение быстрее. Начало причины всего этого заключено в круге, и недаром: ибо вполне оправдано, если что-либо удивительное происходит от чего-то еще более удивительного. Но наиболее удивительно совместное возникновение противоположностей, а круг слагается из таковых. Ведь он сразу же возник из движущегося и покоящегося, чьи природы противоположны друг другу».

Основная часть рассуждений автора сводится к тому, чтобы показать, что один и тот же груз движется тем быстрее, чем дальше он находится от точки опоры рычага, т. е. плечо рычага описывает тем большую дугу, чем оно длиннее.

«Многое удивительное происходит с движениями кругов оттого, что на одной и той же линии, проведенной из центра, ни одна точка не движется с равной скоростью, но всегда более далекая от неподвижного конца движется быстрее...»

Круговое движение точки рассматривается как состоящее из двух движений: тангенциального «сообразно природе» и центростремительного «вопреки природе», которое отклоняет точку от ее естественного прямого пути; отклоняющее движение «вопреки природе» в большом круге меньше, чем в малом. Поэтому за один и тот же промежуток времени точка, более удаленная от центра круга, будет двигаться быстрее и опишет большую дугу, чем менее удаленная.

Далее автор переходит к рассмотрению общего закона рычага, показывая, что равновесие грузов P₁ и Р₂ на его концах зависит от скоростей v₁ и v₂, которые грузы получают при перемещении концов. Свойство рычага связывается со свойством коромысла весов. Весы рассматриваются как прямой равноплечий рычаг первого рода.

Это подтверждает предположение, что закон рычага, по всей вероятности, был практически осознан прежде всего при взвешивании грузов на коромысловых весах (безменах).

«Почему малые силы, как уже было сказано вначале, движут при помощи рычага большие грузы, несмотря на прибавление веса рычага? Ведь легче двигать меньшую тяжесть, а она меньше без рычага. Не оттого ли, что причиной является рычаг, который представляет собой коромысло весов, имеющее веревку снизу и разделенное на неравные части? В самом деле, точка опоры рычага становится здесь заменой веревки, поскольку и та и другая остаются неподвижными в качестве центра. А так как под действием разных тяжестей быстрее движется большая линия, проведенная из центра (в рычаге же имеются три вещи: точка опоры, веревка и центр, во-первых, и, во-вторых и в-третьих, две тяжести – движущая и движимая), то поэтому приводимая в движение тяжесть так относится к приводящей в движение, как одна длина к другой, но в обратном отношении; ведь всегда, чем дальше она отходит от точки опоры, тем быстрее движется. Причина же заключается в сказанном раньше: дальше уходящая из центра описывает больший круг. Таким образом, при одной и той же силе движущая тяжесть, дальше отстоящая от точки опоры, пройдет больше».

Таким образом, если груз А закреплен на конце рычага, то вращать этот груз тем легче, чем дальше от точки опоры движущий груз В. Этот факт автор «Механических проблем» связывает с тем, что движущий груз, укрепленный на большом плече, будет иметь большую скорость v и по отношению к движимому, а следовательно, и больший путь.

Большинство остальных глав трактата посвящено применению правила рычага и решению разнообразных технических задач. Рассматриваются действие гребного весла и руля, действия колес тачки и колесницы, военных метательных машин, условия равновесия тяжелой балки на одной опоре (плечо носильщика) и т. д.

Большой интерес вызывают соображения автора «Механических проблем» о сложении движений. Можно думать, что принцип параллелограмма скоростей и перемещений как в форме сложения, так и в форме разложения движений был известен древним ученым в достаточно развитом виде. В «Механических проблемах» говорится: «Большая линия в равное время описывает больший круг, ибо наружный круг больше внутреннего. Причина этого заключается в том, что линия, описывающая круг, перемещается двумя движениями. Итак, когда она перемещается при определенном соотношении между обоими, она движется необходимо по прямой, и эта прямая становится диагональю той фигуры, которая образуется из линий, сочетаемых в указанном соотношении».

Анализ способа построения касательной к спирали в книге Архимеда «О спиралях» говорит о том, что Архимеду также был известен закон сложения скоростей. Наконец, вся эллинистическая астрономия при описании движений небесных тел основывается на правилах сложения круговых движений.

Архимед – подлинный основатель теоретической статики и гидростатики.

Уже на самых первых этапах научной деятельности, по-видимому, механика интересовала Архимеда больше всего, причем переход к теоретическим обобщениям шел от чисто прикладных вопросов. Но и позже, помимо теоретических исследований в области математики, физики и Механики, Архимед занимался вопросами прикладной механики, в частности в связи с потребностями обороны его родного города Сиракузы. Он обогатил античную технику большим количеством замечательных изобретений. Древние авторы приписывали Архимеду изобретение так называемой улитки – водяного винта, служившего для поливки полей в Египте (правильнее говорить в этом случае об его усовершенствовании). Рассказывают также, что при помощи механических приспособлений Архимед передвигал по суше тяжело нагруженный корабль сиракузского тирана Гиерона. Свидетельства древних расходятся в том, каковы были эти приспособления: одни говорят о рычаге, другие – о полиспасте, третьи – о зубчатых колесах, четвертые – о колесах, т. е. указывают почти все так называемые простые машины. Во время осады Сиракуз римлянами, по рассказу Плутарха (в биографии Марцелла), жители города применяли для обороны военные машины, сооруженные по указаниям Архимеда: орудия, метавшие снаряды, поворотные краны («клювы»), низвергающие огромные камни на вражеские корабли, привязанные к цепям железные лапы, которые захватывали нос корабля и ставили корабль вертикально на корму.

Из сочинений Архимеда, посвященных механике, до нас дошли трактаты в двух книгах «О равновесии плоских фигур, или О центрах тяжести плоских фигур», трактат «О плавающих телах», также в двух книгах, и «Эфод, или Послание к Эратосфену о механических теоремах».

Первыми сочинениями Архимеда по механике были «Книга опор» и «О весах». Поскольку они до нас не дошли, об их содержании можно судить лишь по ссылкам в более поздних работах Герона и Паппа, а также по комментариям Евтокия и Симпликия. Анализ упомянутых сочинений показывает, что во время их написания Архимед еще не знал, что вес тела можно считать сконцентрированным в его центре тяжести, хотя и пользовался последним понятием. Понятие о центре тяжести появилось у Архимеда в итоге практического изучения распределения груза между опорами. Рассматривая давление балки на опоры, Архимед приходит, правда, к неверным результатам, но отсюда он перешел к одноопорной балке – рычагу. Эти ранние работы интересны тем, что в них кроме понятия центра тяжести появляется и понятие центра момента. Папп приводит следующее определение Архимеда для центра тяжести: «Центром тяжести некоторого тела называется некоторая расположенная внутри него точка, обладающая тем свойством, что если за нее (мысленно) подвесить тяжелое тело, то оно останется в покое и сохранит первоначальное положение». Из комментария Евтокия известно определение центра момента. «Архимед называет центром момента плоской фигуры точку, при подвешивании за которую фигура остается параллельной горизонту; центром момента двух или более плоских фигур он называет точку подвеса рычага, остающегося параллельным горизонту, если прикрепить к его концам указанные фигуры».

Теория центра тяжести с точки зрения практической механики, возможно, была развита в дошедшей до нас в виде отдельных фрагментов книге «О рычагах». Математическое изложение теории центра тяжести, очевидно, впервые приведено также в не дошедшем до нас трактате «О равновесии», значительно большем по объему, чем «О равновесии плоских фигур».

В первой книге трактата «О равновесии плоских фигур» изложена теория равновесия рычага. Однако этот трактат имеет гораздо более важное значение: это основы общей теории равновесия, построенной на системе аксиом.

Исходя из действительных и простейших фактов опыта, Архимед сумел обобщить эмпирический материал техники D привести его с помощью математики в научную систему.

Теория рычага основана на следующих предпосылках, которые Архимед считает очевидными:

«1. Равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивают тяжести на большей длине.

2. Если при равновесии тяжестей на каких-нибудь длинах к одной из тяжестей будет что-нибудь прибавлено, то они не будут уравновешиваться, но перевесит та тяжесть, к которой было прибавлено.

3. Точно так же, если от одной из тяжестей будет отнято что-нибудь, то они не будут уравновешиваться, но перевесит та тяжесть, от которой не было отнято.

4. При совмещении друг с другом равных и подобных плоских фигур совместятся друг с другом и их центры тяжести.

5. У неравных же, но подобных фигур центры тяжести будут подобно же расположены.

6. Если величины уравновешиваются на каких-нибудь длинах, то на тех же самых длинах будут уравновешиваться и равные им.

7. Во всякой фигуре, периметр которой везде выпукл в одну и ту же сторону, центр тяжести должен находиться внутри фигуры».

Заметим, что когда Архимед говорит о действии на рычаг подвешенных грузов (тяжестей), он основывается на свойствах центра тяжести, понятие которого считает известным; это также говорит в пользу предположения о том, что этот трактат был не первым его механические сочинением.

В частности, предполагается, что центр тяжести тела, свободно висящего на нити, располагается на линии нити и что подвешенные тела действуют на рычаг в точке подвеса весом, сосредоточенным в центре тяжести. В последующих доказательствах Архимед имеет дело лишь с весами тел и их центрами тяжести.

Далее Архимед доказывает семь теорем, первые три из которых разъясняют смысл сформулированных выше предпосылок. Так, теорема III гласит: «Неравные тяжести будут уравновешиваться на неравных длинах, причем большая тяжесть на меньшей длине».

В теореме IV определяется центр тяжести системы двух тел: «Если две равные величины не имеют одного и того же центра тяжести, то для величины, составленной из обеих этих величин, центром тяжести будет середина прямой, соединяющей центры тяжести этих величин».

В теореме V Архимед применяет этот метод к системе трех тел, расположенных так, что центр тяжести среднего из них находится в середине отрезка, соединяющего центры тяжести крайних. Согласно этой теореме, центр тяжести такой «составной величины» совпадает с центром тяжести среднего тела.

Особо можно выделить теоремы VI и VII, в которых формулируется и доказывается основной закон рычага.

Теорема VI формулируется следующим образом: «Соизмеримые величины уравновешиваются на длинах, которые обратно пропорциональны их тяжестям».

В теореме VII закон равновесия рычага распространяется на случай несоизмеримых фигур. В теореме I второй книги трактата этот закон распространяется на случай криволинейных квадрируемых фигур.

Помимо указанных выше принципов Архимед пользуется в ходе доказательств еще одним, который, однако, в числе исходных предпосылок явно не фигурирует. Этот принцип можно сформулировать следующим образом: равновесие рычага не нарушится, если груз, подвешенный в точке А рычага, заменить двумя равными грузами половинного веса, точки подвеса которых расположены симметрично относительно точки подвеса замещаемого груза. Это положение мы будем называть принципом замещения. Хотя в ходе доказательств принцип замещения Архимед применяет с достаточной отчетливостью, однако он оградил бы свое сочинение от упреков самых требовательных критиков, если бы поставил его в число своих исходных предпосылок.

Заметим также, что аксиомы Архимеда являются первым существенным шагом в развитии понятия момента силы. Архимед с достаточной ясностью отмечает, что действие подвешенного груза на рычаг пропорционально его весу и расстоянию точки подвеса от точки опоры рычага. Оставалось лишь найти форму этой зависимости – и Архимед ее нашел. Он доказал, что действие подвешенного груза на рычаг прямо пропорционально величине груза и расстоянию точки приложения от неподвижной опоры рычага.

«Вникнув в сущность архимедовых аксиом,- писал академик А. Н. Крылов, - мы видим, что он ввел здесь новый элемент, производящий движение, именно произведение силы на ее расстояние до точки опоры, - то, что было впоследствии названо моментом силы и что производит вращательное движение тела». Первая книга трактата «О равновесии плоских фигур» заканчивается определением центров тяжести параллелограмма, треугольника и трапеции.

Во второй книге трактата Архимед переходит к определению центров тяжести фигур, образуемых при пересечении параболы прямой. Доказывается ряд теорем (предложений), например: «Если две площади, ограниченные (каждая) прямой и параболой и могущие быть приложенными к заданной прямой, не имеют одного и того же центра тяжести, то для величины, составленной из них обеих, центр тяжести будет на прямой, соединяющей их центры тяжести, причем вышеупомянутую прямую он разделит таким образом, что ее отрезки будут обратно пропорциональны этим площадям».

«У всякого сегмента, ограниченного прямой и параболой, центр тяжести делит диаметр сегмента так, что прилежащий к вершине сегмента отрезок в полтора раза больше отрезка у основания».

Эти предложения тесно связаны с работами Архимеда по геометрии. Примером применения теоретических положений механики к геометрии может также служить определение площади сегмента параболы, основанное на законе рычага и теоремах о центре тяжести плоских фигур, которое приведено в математическом сочинении Архимеда «Квадратура параболы». О тесной связи методов механики и математики в творчестве Архимеда свидетельствует «Эфод, или послание к Эратосфену о механических теоремах». В этом произведении механика рассматривается как средство решения геометрических задач. Правда, Архимед не считал механический метод строгим, он рассматривал его как удобный прием для получения некоторых геометрических результатов, которым после этого надлежало дать строгое геометрическое доказательство.

Среди теорем «Эфода» большой интерес представляет лемма о центре тяжести конуса, для доказательства которой Архимед разбивает конус плоскостями, параллельными основанию, на тонкие диски равной высоты. Нахождение центра тяжести конуса сводится к нахождению центра тяжести сегмента параболы.

Другим замечательным трудом Архимеда по механике является его более поздний трактат «О плавающих телах». Существует предположение, что это была вообще его последняя работа. Согласно легенде, Архимед пришел к открытию своего основного гидростатического закона случайно, решая задачу о составе короны, которую царь Гиерон заказал сделать из золота, но подрядчик изготовил из сплава золота и серебра.

Античная легенда рассказывает о повелении Гиерона и о случайном наблюдении Архимеда, принимавшего ванну. В действительности же открытие основного закона гидростатики было итогом многовековых эмпирических наблюдений и целой цепи теоретических размышлений.

Представление о частицах жидкости, выталкиваемых более плотными телами, напоминает теории древних атомистов. У Архимеда также находят более правильную и точную формулировку соображения Аристотеля о равновесии и движении тел в различных материальных средах.

В основу всех его выводов положена следующая гипотеза: «Предположим, что жидкость имеет такую природу, что из ее частиц, расположенных на одинаковом уровне и прилежащих друг к другу, менее сдавленные выталкиваются более сдавленными, и что каждая из ее частиц сдавливается жидкостью, находящейся над ней по отвесу если только жидкость не заключена в каком-нибудь сосуде и не сдавливается еще чем-нибудь другим».

В первых двух предложениях трактата Архимед устанавливает шарообразность свободной поверхности воды, окружающей Землю, и совпадение центра этого шара с центром Земли. Опираясь на эти предпосылки и исходя из того, что поверхность жидкости имеет сферическую форму, Архимед доказывает следующие положения:

1. Тела, равнотяжелые с жидкостью, будучи опущены в эту жидкость, погружаются так, что никакая их часть не выступает над поверхностью жидкости, и не будут двигаться вниз (предложение III).

2. Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, не погружается целиком, но некоторая часть его остается над поверхностью жидкости (предложение IV).

3. Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, погружается настолько, чтобы объем жидкости, соответствующий погруженной (части тела), имел вес, равный весу всего тела (предложение V).

4. Тела, более легкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх с силой, равной тому весу, на который жидкость, имеющая равный объем с телом, будет тяжелее этого тела (предложение VI).

5. Тела, более тяжелые, чем жидкость, опущенные в эту жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела (предложение VII).

Далее исследуются вопросы равновесия и устойчивости плавающих тел. Основным методом исследования является способ возмущения состояния равновесия.

Все положения трактата доказываются с помощью единого приема определения центра тяжести всего тела и выступающей части и центра тяжести объема погруженной части тела. Условием равновесия тела является расположение этих точек на одной отвесной линии, когда сила тяжести и сила гидростатического давления, действуя в противоположные стороны вдоль одной прямой, взаимно уравновешиваются при погружении тела в жидкость. Равновесие устойчиво, если при отклонении тела от положения равновесия оно стремится возвратиться в это положение.

Во второй части трактата рассматриваются разнообразные случаи равновесия и устойчивости плавающих в жидкости сегментов сферы и параболоида вращения.

«Эта книга, - писал Лагранж, - является одним из прекраснейших памятников гения Архимеда, она содержит в себе теорию устойчивости плавающих тел, к которой современные ученые прибавили лишь очень немного».

Интересно, что методы, применявшиеся в теории корабля в XVIII в. и позже, имеют немало общего с архимедовским методом изучения плавания сегмента параболоида. Однако Архимед рассмотрел только частные случаи, не создав общей теории.

Несмотря на замечательные исследования Архимеда по гидростатике, мы встречаем в античной науке и после него весьма смутные, а нередко и ложные представления о гидростатических явлениях.

Правильные представления о давлении внутри жидкости были достигнуты лишь в XVI – XVII вв. на основе работ Галилея, Паскаля и Стевина.

Развитие механики в эпоху эллинизма связано прежде всего с именем представителя Александрийской научной школы Герона Александрийского, известного также под именем Герона-Механика. О времени жизни и деятельности этого ученого точных сведений не сохранилось; в настоящее время большинство историков науки считают, что он жил в I – II вв. н. э.

Основное сочинение Герона по механике, обычно называемое «Механикой» Герона, сохранилось только в арабском переводе сирийца Косты ибн-Луки, жившего в конце IX и начале X в. Точное название этого сочинения, согласно Косте ибн Луке, - «Книга Герона о поднимании тяжелых предметов». Это сочинение появилось в 1894 г во французском переводе Карра де Во, а в 1900 г. – в немецком переводе Л. Никса. К обоим переводам приложен арабский текст, а к немецкому, кроме того, отрывки греческого текста, сохранившиеся в передаче Паппа Александрийского.

«Механика» Герона состоит из трех книг. Первая книга посвящена теоретическим вопросам. Здесь наряду с некоторыми чисто геометрическими построениями рассматриваются передача движения с помощью зацепленных кругов, сложение движений по правилу параллелограмма, распределение нагрузки между опорами; определяется центр тяжести. Как указывает Герон, он излагает содержание не дошедшей до нас «Книги опор» Архимеда. Герон пишет: «Нам совершенно необходимо разъяснить кое-что о давлении, передаче и переносе с количественной стороны в той мере, в которой это нужно для изучающих».

Во второй книге «Механики» дается описание пяти простых машин: рычага, ворота, клина, винта и блока. Герои указывает, что в изложении теории рычага он развивает идеи Архимеда из «Книги о равновесии». Помимо описания действия этих машин рассматриваются также соединения рычага, блоков, ворота и винта.

В этой книге даются ответы на 17 вопросов, относящихся к практическому применению простых машин, а также определяются центры тяжести различных фигур. В третьей книге описаны различные конструкции приборов для поднятия тяжестей и прессов, основанных на комбинациях простых машин.

В то же время трактат Герона главным образом представляет собой дальнейшее развитие кинематического варианта статики, восходящего к «Механическим проблемам». Основной метод изучения равновесия у Герона – изучение перемещений, которые получают точки приложения сил при нарушении этого состояния. В результате он вплотную подошел к элементарной форме принципа возможных перемещений - «золотому правилу механики», которое формулирует следующим образом: «Отношение движущей силы ко времени является обратным».

Замечательно следующее рассуждение Герона: «Некоторые люди думают, что тяжести, лежащие на земле, могут быть сдвинуты с места только путем приложения эквивалентной им силы. Этот взгляд ложен. Итак, докажем, что тяжести, лежащие так, как было сказано, могут быть сдвинуты с места посредством силы, меньшей, чем любая известная, и раскроем причину, почему подобное явление не оказывается сразу приметным. Представим себе, стало быть, что груз лежит на земле и что этот груз равномерный, гладкий и плотный. Пусть плоскость, на которой груз лежит, может быть наклонена в обе стороны, а именно вправо и влево. Пусть сначала она будет наклонена вправо. Тогда оказывается, что данный груз скатывается вправо, ибо естественным для грузов является стремление двигаться вниз, если их ничто не подпирает, препятствуя их движению. Если, далее, наклонная сторона опять поднимается до горизонтальной плоскости и вся плоскость придет в состояние равновесия, то тогда груз пребудет в этом положении. А если она наклонится в другую сторону, т. е. в левую, то и груз будет клонить в ту же сторону, даже при самом незначительном наклоне. Следовательно, груз нуждается не в силе, которая его движет, а в силе, которая его подпирает, препятствуя его движению. Допустим теперь, что груз опять приходит в положение равновесия и не склоняется в какую-либо сторону, - тогда он остается в том же положении и пребывает в покое, пока плоскость не наклонится в какую-нибудь сторону, - в последнем случае и он клонит в ту же сторону. Итак, груз, готовый обратиться к любому направлению, нуждается лишь в незначительной силе, чтобы прийти в движение, и притом в соответствии с силой, которая придает ему наклон. Выходит, что груз может быть приведен в движение любой самой малой силой».

Герону принадлежат также три трактата по прикладной механике: «Пневматика» - о механизмах, приводимых в действие нагретым или сжатым воздухом или паром, «Об автоматах» - о конструкциях самодвижущихся приборов и «Белопойика» - о конструкциях луков, катапульт и других видов оружия. Из многочисленных механизмов, сконструированных Героном, отметим шар, вращающийся под действием пара, автомат для открывания дверей храма при зажигании огня на алтаре, пожарный насос, водяной орган, механический театр марионеток. В «Пневматике» имеются и теоретические рассуждения: Герон объясняет упругость воздуха и пара соударениями мельчайших частиц, из которых, по его мнению, состоят воздух и пар. Некоторые рассуждения Герона показывают, что, хотя он был знаком с гидростатическими законами Архимеда, физическая причина кажущейся потери веса погруженных в жидкость тел была ему не известна; он считал эту потерю веса абсолютной.

Представителем Александрийской школы был римский архитектор эпохи Августа – Марк Поллион Витрувий (1в. до н. э.). Десятая книга его знаменитого трактата «Об архитектуре» целиком посвящена механике. Витрувий был строителем-практиком. Поэтому механическая часть его трактата содержит главным образом описание различных механизмов для поднятия тяжестей, а также практических правил и строительных рецептов. Специальный раздел посвящен военным машинам. Витрувий дает следующее определение машины: «Машина есть сочетание соединенных вместе деревянных частей, обладающее огромными силами для передвижения тяжестей».

В 8-й главе X книги трактата рассматривается принцип действия механизмов, основанный на теории равновесия рычага, которую Витрувий излагает согласно «Механическим проблемам» и Герону, придерживаясь, таким образом, кинематического варианта статики.

Механике посвящена и последняя (VIII) книга «Математического собрания» Паппа Александрийского (III в. н. э.). Папп проводит в ней различие между механикой – теоретической наукой и механикой – практическим искусством. Сочинение Паппа представляет собой в основном компилятивный труд, в который включены разнородные сведения из различных источников. В книге приведено большое число отрывков из сочинений Архимеда, некоторые теоремы геометрической статики, относящиеся к определению положения центров тяжести различных фигур, главным образом трапеции и треугольника. Папп рассматривает приложение геометрической статики к конкретным техническим вопросам, например задачу об определении силы, необходимой для того, чтобы на наклонной плоскости сдвинуть груз, который на горизонтальной плоскости сдвигается данной силой. С другой стороны, в трактат включено описание устройства грузоподъемных машин из «Механики» Герона, однако без изложения принципа их действия.

В книге содержатся и собственные исследования автора, например теоремы об объемах тел вращения, которые он выражает через длину окружности, описываемой центром тяжести вращающейся фигуры (теорема Паппа – Гюльдена).

Сочинения Герона и Паппа показывают, что александрийские ученые I – IV вв. н. э. уделяли значительное внимание как теоретическим основам механики (хотя научный уровень их работ был значительно ниже, чем у Архимеда), так и практической механике, конструированию механизмов, оружия и автоматов.

Одним из основных стимулов разработки принципов кинематики и источников развития кинематических представлений в механике была греческая астрономия.

В вавилонской астрономии положения светил на небесной сфере вычислялись арифметическими методами.

Как мы уже упоминали, представители греческой классической философии (Платон, Аристотель) считали круговое движение, свойственное небесным телам, «совершенным». Поэтому греческие астрономы, обращаясь к кинематико-геометрическому моделированию видимых движений небесных тел, представляли эти сложные движения только в виде комбинации нескольких круговых. Первая попытка такого моделирования – теория вращающихся концентрических сфер, предложенная крупнейшим античным математиком и астрономом Евдоксом Книдским (IV в. до н. э.). Теория Евдокса состоит в следующем: вокруг центра, в котором находится покоящаяся Земля, вращаются 27 концентрических сфер. На внешней сфере расположены «неподвижные» звезды. С помощью остальных сфер Евдокс объясняет движение Солнца, Луны и пяти планет. Каждое из упомянутых небесных тел неразрывно связано с некоторой равномерно вращающейся сферой, объемлющей другую, ось которой находится под известным углом к оси первой. Внутренняя вращающаяся сфера увлекается в своем вращении внешней.

Движение Луны описывается с помощью трех сфер. Внешняя сфера Луны, на которой расположена эклиптика, служит для объяснения суточного движения Луны. Она, как и сфера «неподвижных» звезд, совершает один оборот в сутки вокруг полюсов экватора.

Вторая сфера, на которой расположена наклонная к эклиптике орбита Луны, участвуя в движении первой, вращается вокруг полюсов эклиптики, чем объясняется «отступание узлов» лунной орбиты. Третья сфера, на которой расположена Луна, вращается вокруг полюсов лунной орбиты, участвуя, таким образом, в движении обеих внешних сфер.

Движение планет Евдокс объясняет с помощью четырех сфер. Внешняя сфера, совершающая, как и в случае Луны, одно движение, совпадающее с суточным движением «неподвижных» звезд, служит для объяснения суточного движения планет. Вторая сфера, участвуя в движении первой, совершает оборот вокруг полюсов эклиптики за время, равное периоду обращения планеты. Вращения третьей и четвертой сфер служат для объяснения прямого и возвратного движений планет. Третье вращение, полюсами которого служат две неподвижные точки на эклиптике, совершается перпендикулярно ей. Плоскость четвертого вращения наклонена к плоскости третьего. В результате этих двух движений траектория планеты имеет вид петлеобразной кривой в форме лежащей восьмерки – гиппопеды, большая ось которой расположена на эклиптике.

Центр ее вследствие второго вращения проходит за период обращения планеты всю эклиптику.

С помощью системы Евдокса можно было более или менее удовлетворительно описать движение внешних планет (Юпитера и Сатурна).

Астроном Калипп пытался усовершенствовать эту систему, добавив еще по две сферы для Солнца и Луны и по одной для каждой из планет. Аристотель, добавив «вращающиеся назад» сферы, при помощи движения которых он рассматривал вращение любой сферы независимо от объемлющей ее, увеличил их число до 56.

Основным недостатком как гипотезы Евдокса, так и ее улучшенных вариантов было то, что, согласно концентрической модели, расстояния планет от Земли предполагаются неизменными.

Другая, более совершенная кинематико-геометрическая модель движения небесных тел была предложена Аполлонием и развита затем Гиппархом и Птолемеем.

Кинематико-геометрическое моделирование движения небесных тел тесно связано с общими успехами кинематического метода в греческой математике. Античные математики часто обращались к кинематическому методу при решении многих задач, связанных с построением и исследованием кривых.

Архит Тарентский (IV в. до н. э.) конструировал специальные приборы для вычерчивания кривых. Гиппий Элидский, живший около V в. до н. э., построил путем сложения равномерных поступательного и вращательного движений кривую, называемую квадратрисой, которой воспользовался при рассмотрении задачи о трисекции угла.

Аналогичным путем Никомед (II в. до н. э.) определил конхоиду.

К кинематическому методу часто обращался Архимед. Вот, например, его определение спирали: «Если на плоскости проведена прямая линия, которая, сохраняя один свой конец неподвижным и вращаясь с одинаковой скоростью, любое число раз вернется в исходное положение, и если одновременно с вращением этой линии какая-нибудь точка будет с постоянной скоростью перемещаться по этой прямой, начиная движение из неподвижного конца, то эта точка опишет на плоскости спираль».

Заметим, что кинематические расчеты применялись также при изготовлении различного рода автоматов (счетчики проходимых расстояний, часы и т. д.). Так, например, Архимед изготовил знаменитую модель небесной сферы, в которой автоматически воспроизводились видимые движения светил. Архит сконструировал прибор для нахождения двух средних пропорциональных к двум отрезкам (к чему, как известно, может быть сведено решение задачи об удвоении куба). Решение Архита по существу сводится к построению координат точки пересечения трех поверхностей вращения: цилиндра, конуса и тора.

Следует отметить, что применение механических устройств к геометрии встречало осуждение у философов-идеалистов, и прежде всего у Платона. По этому поводу Плутарх в своих «Сравнительных жизнеописаниях» говорит: «Знаменитому и многими любимому искусству построения механических орудий положили начало Евдокс и Архит, стремившиеся сделать геометрию более красивой и привлекательной, а также с помощью чувственных, осязаемых примеров разрешить те вопросы, доказательство которых посредством одних лишь рассуждений и чертежей затруднительно; такова проблема двух средних пропорциональных – необходимая составная часть многих задач, для разрешения которой оба применили механическое приспособление, строя искомые линии на основе дуг и сегментов. Но так как Платон негодовал, упрекая их в том, что они губят достоинство геометрии, которая от бестелесного и умопостигаемого опускается до чувственного и вновь сопрягается с телами, требующими для своего изготовления длительного и тяжелого труда ремесленника, - механика полностью отделилась от геометрии и, сделавшись одною из военных наук, долгое время вовсе не привлекала внимания философии».

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00