Главная
Тема 31. Пьер
Симон Лаплас. Возникновение небесной
механики
Закон всемирного тяготения, выведенный Ньютоном,
позволил Пьеру Симону Лапласу (1749—1827)
в конце XVIII в. разобраться в механике Солнечной системы и определить
устойчивость движений небесных тел. Необъясненным оставалось лишь перемещение
перигелия Меркурия, которое удалось получить в наше время на основе
релятивистской механики.
Лаплас родился в семье крестьянина в Бомоне, небольшом
местечке Нормандии. Первые годы его жизни мало известны.
После окончания Бомонского колледжа, где он увлекался
математикой, двадцатилетний Лаплас порывает со своими родителями й уезжает в
Париж. У него были рекомендации, с которыми он явился к Д'Аламберу. Лаплас во
время ожидания приема изложил свой мнения о механике, которые так понравились Д'Аламберу,
что тот написал Лапласу письмо с назначением свидания, после чего Лаплас
получил место преподавателя математики в Парижской военной школе. Он принял все
меры, чтобы попасть в Академию. После первой неудачи в Париже он хотел получить
место в Берлине, по Лагранж,
ставший президентом Берлинской Академии после отъезда Эйлера в Россию в 1766
г., отсоветовал ему ехать в Берлин» и в 1773 г. Лаплас делается адъюнктом, а в
1785 г. — полноправным членом Парижской Академии.
Два предмета привлекали молодого Лапласа: теория
вероятностей и небесная механика, которой он посвятил свою жизнь. Плодом его
трудов была пятитомная «Небесная механика», написанная в период 1793—1825 гг.
Основной трудностью при определении движения какой-либо планеты была
необходимость учета притяжений и других планет, вызывавших определенные
неравенства в движении. Эти неравенства могли быть вековыми (постоянными),
накоплявшимися со временем, и периодическими, не влиявшими особенно сильно на
движение планеты. Постоянные неравенства могли совершенно изменить движение
планет и даже разрушить устойчивость движения Солнечной системы; поэтому они
доставляли много беспокойства и неприятностей вычислителям.
Лаплас начал эту работу с 1773 г. Ему удалось
показать, что ряд возмущений в планетных движениях, которые считались вековыми,
в действительности после тщательного анализа оказались периодическими. Двенадцать
лет потребовалось Лапласу, чтобы вполне разобраться в этом деле, и еще шесть
лет для того, чтобы подготовить материал к составлению своего основного
сочинения, первый том которого вышел в 1794 г.
Все сочинение состоит из шестнадцати книг, первая из которых
была посвящена теоретической механике. В этой книге он говорит о силах, их
измерении, условиях равновесия (по принципу возможных перемещений) и об
уравнениях движения точки и системы, а также о семи основных интегралах —
движения центра тяжести, законы площадей и кинетической энергии. Для системы,
на которую не действуют никакие внешние силы (а такой считалась Солнечная
система), он формулирует закон сохранения площадей (кинетического момента) и
определяет так называемую неизменяемую плоскость Лапласа, перпендикулярную к
направлению кинетического момента всей Солнечной системы.
Вторая книга посвящена общим законам движения планет и
ряду последовательных приближений, которые приходится делать при вычислении
этих движений. Затем идут книги, трактующие о форме небесных тел, теории
приливов и вращении планет вокруг собственных осей (третья — пятая книги).
Третий и четвертый тома, вышедшие в 1802—1805 гг.,
посвящены определению движений каждой из планет Солнечной системы в
отдельности, Луны, спутников и комет (шестая—девятая книги). Десятая книга
трактует об отдельных частных вопросах (рефракции и т. д.); в ней дается
изложение теории капиллярных явлений.
Наконец, вышедший за два года до смерти Лапласа пятый том (1825)
содержит дополнения, из которых для нас интересна двенадцатая книга — изложение
вопросов притяжения сфер.
Результат работы Лапласа показал, что при помощи
введенной Ньютоном силы всемирного тяготения можно совершенно точно представить
движение всех тел Солнечной системы (кроме движения перигелия Меркурия). Это
вызвало у Лапласа уверенность, что теория всемирного тяготения сможет объяснить
и молекулярные силы; в частности, этого вопроса касалась разработанная Лапласом
теория капиллярности. Следует, однако, отметить, что дальнейшего развития молекулярная
механика не получила: основная причина заключалась в неизвестности законов,
которые управляют этими явлениями. Возрождение этой теории на более высоком
уровне намечается лишь в наше время в связи с развитием физики элементарных
частиц.
В 1812 г. вышел из печати второй большой труд Лапласа
«Теория вероятностей». Занятия Лапласа этим вопросом имеют значение для его
космогонической теории, получившей большую известность в течение XIX в. Эта
теория резко выделяется из ряда других произведений Лапласа. Космогоническая
теория Лапласа подвергалась математической обработке значительно позже у его
последователей; сам Лаплас в вышедшей в 1796 г. работе «Изложение системы мира»
поместил эту теорию в приложении «с осторожностью, которую должно внушать все то,
что не является результатом наблюдения или расчета».
Лаплас считал, что на месте Солнечной системы была
когда-то огромная газовая туманность, простиравшаяся далеко за пределы самой
крайней планеты. Частицы этой туманности обладали беспорядочным движением,
которое управлялось лишь законами случайности. Не было такого направления, по
которому частицы двигались бы преимущественно перед всеми другими, так что всю
туманность можно было считать находившейся как бы в покое. Никаких внешних сил
на эту туманность не действовало и никакие связи не стесняли свободу ее
движений; между частицами действовали только силы всемирного притяжения.
Тогда основные законы позволяли утверждать следующее:
1. Центр инерции этой туманности находится в покое или
двигается прямолинейно и равномерно.
2. Кинетический момент туманности остается постоянным
относительно любого центра.
Пусть этот центр будет центром инерции туманности. По
отношению к нему можно считать туманность находящейся в покое и все частицы
движущимися беспорядочно; для наблюдателя, находящегося в этом центре, примерно
столько же частиц кажутся движущимися по вращению стрелки часов, сколько и
против вращения стрелки. Но можно ли утверждать, что ровно половина всех частиц
должна двигаться по направлению стрелки, а другая — против него?
Если эти направления равновероятны (при наличии
беспорядочности движения), то отношение чисел частиц, движущихся в ту и в
другую сторону, при бесконечном возрастании их числа стремится к единице, но
разность этих чисел, как показывает теория вероятностей, не стремится к нулю;
она возрастает по мере увеличение числа членов. Возрастание этой разности
будет, конечно, отставать от возрастания числа частиц (если их число возрастает
в n раз, то разность увеличится
примерно в 
раз), но может
стать достаточно большой.
Это показывает, что и в случае первоначальной газовой
туманности между числами частиц, движущихся в противоположных направлениях,
должна быть некоторая чисто случайная разность; следовательно, кинетический
момент рассматриваемой туманности не будет равным нулю, и его начальное
значение должно сохраняться постоянным в течение всего времени существования
туманности. Если это значение не очень велико, то в начальных стадиях
туманность можно считать практически не вращающейся; во всяком случае это вращение заметным не будет.
Но по мере того как в результате взаимного притяжения
частиц туманность сжимается и радиус уменьшается, трансверсальные (поперечные)
скорости частиц будут увеличиваться и бывшее сначала незаметным вращательное движение
туманности все время возрастает. Настанет момент, когда вращение станет
настолько сильным, что крайние частицы оторвутся, образуя кольцо, которое в
свою очередь сожмется в планету, унося некоторый вращательный момент; этот
момент проявится в двух формах — планета получит трансверсальную скорость,
заставляющую ее совершать обороты вокруг Солнца, и, кроме того, будет вращаться
вокруг собственного центра; этот вращательный момент при дальнейшем сжимании
оторвавшейся массы может породить спутников планеты, а затем сохраниться в виде
вращения планеты вокруг собственной оси.
Гипотеза Лапласа объяснила, почему центр инерции
Солнечной системы практически совпадает с центром Солнца, почему орбиты планет
находятся в одной примерно плоскости и почему направления движения планет
вокруг Солнца одинаковы и совпадают с направлением вращения самих планет вокруг
своей реи, а также и с направлением движения вокруг планет их спутников; даже
направление собственного вращения Солнца вокруг своей оси остается таким же, как
и направление движения планет вокруг Солнца.
В дальнейшем развитии науки встретились некоторые
трудности: так, спутники Урана вращаются в плоскости, почти перпендикулярной к
плоскости экватора, некоторые спутники вращаются в направлении, обратном направлению
общего вращения, но, самое главное, оказалось, что кинетический момент Солнца
(в его вращении вокруг собственной оси) гораздо меньше общего кинетического
момента всех остальных планет, несмотря на то что
общая их масса несравнима с массой Солнца. Это обстоятельство заставило в
настоящее время отказаться от гипотезы Лапласа, громадное историческое значение
которой остается несомненным: это была первая теория, объясняющая движение
Солнечной системы без божественного вмешательства.
Лаплас принадлежал к числу людей, поражавших своей
разносторонностью;, хотя наибольших результатов он
достиг в области небесной механики, но он много сделал также и в области
анализа, теории вероятностей и теоретической механики.
В области механики Даллас придерживался традиций
Лагранжа или школы кинетической энергии, хотя этого термина тогда еще не
существовало: употребляли термин «живая сила». Как показано выше, понятие о
силе как векторе можно совершенно естественно получить из представления о силе
как производной по времени от количества движения. В случае прямолинейного
движения точки силу, действующую на нее, можно определить тоже при помощи
производной:
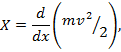
но приведенная формула применима только к прямолинейному движению.
В криволинейном движении точки теорему кинетической
энергии выразим в виде
где
X, Y, Z — суть составляющие силы по
координатным осям.
Если стоящее в правой части выражение элементарной
работы представляет полный дифференциал некоторой функции U от координат точки (Лагранж обозначал ее П, не давая ей никакого
названия), то уравнение кинетической энергии допускает интеграл
Если ввести обозначения 
для
кинетической энергий и 
, то получим закон сохранения механической энергии
откуда
.
Функцию U
Гамильтон назвал силовой. Так как
то
имеем нечто, аналогичное производной по времени от количества движения, но
только в том случае, если силовая функция существует, что бывает не для всех
сил. Очень существенно, что силовая функция имеется для наиболее важных сил, в
том числе для всемирного тяготения, при исследовании которого она и была
введена. Но ее появление было очень существенным шагом в развитии механики. До
сих пор в механике рассматривались материальные точки или твердые тела, имеющие
определенный (конечный) объем и величину. Силовую функцию U(x, у, z) можно рассматривать как характеризующую поле —
пространство, каждой точке которого соответствует определенное число, которое
получим, если подставив значения координат этой точки в выражение U(x, у, z).
Таким образом, получается так называемое скалярное
поле. Можно пойти дальше и каждой точке отнести определенный вектор: тогда
получим векторное поле, в частности силовое поле. При существовании силовой
функции U(x, у, z) каждой точке
соответствует сила, определяемая выражением
Можно образовать эту силу при помощи некоторой
операции, которую можно получить, обобщив понятие производной.
Производная 
функции 
определяется
как предел выражения
Рассмотрим
∆x как интервал изменения
переменной, принимающей по его концам значения f(x) и f(х+∆x).
Предположим, что ∆х—высота
призмы, основания которой равны единице; объем этой призмы 
. Затем на основаниях призмы отметим единичные векторы
нормалей: при входе —1, а при выходе +1. Тогда выражение, сгоящее
в числителе дроби, можно представить в виде
и рассматривать
его как сумму двух площадей, помноженных каждая на соответствующее значение
функции и единичный вектор нормали. Выражение, предел которого хотим найти,
можем рассматривать как распространенную по поверхности полученной призмы сумму
указанных произведений, деленную на объем этой призмы ∆V. Тогда
Эту операцию распространим и на случай скалярного
поля, образованного значениями силовой функции U. Так как значения этой функции изменятся не только по одному направлению,
то окружим рассматриваемую точку замкнутой поверхностью S, разобьем ее на элементы dS, имеющие нормали, определяемые единичными векторами 
, которые умножим на соответствующие значения функции U, и берем сумму всех таких площадок.
Полученный интеграл по замкнутой поверхности принято выражать в виде
.
Эту сумму делим на объем V, ограниченный замкнутой поверхностью, и отыскиваем предел этой
дроби, стягивая объем в точку. Полученное выражение обозначаем 
:
.
Математики доказывают, что величина этого предела не
зависит ни от формы замыкающей поверхности, ни от процесса стягивания ее в
точку. Поэтому возьмем рассматриваемую поверхность форме параллелепипеда, ребра которого dx, dy, dz параллельны направлениям координатных осей; единичные векторы нормалей к граням параллелепипеда соответственно 
. Пусть рассматриваемая функция в
точке, лежащей в центре этого параллелепипеда, имеет значение Uо, расстояния от
нее до граней параллелепипеда соответственно 
.Тогда интеграл представится в виде суммы трех пар площадок —
граней рассматриваемого параллелепипеда, помноженных на соответствующие
значения функции U и на единичные
векторы нормалей. Для пары
площадок, перпендикулярных к оси х,
получим слагаемые
и
аналогично для остальных осей:
Сумма этих слагаемых после очевидных сокращений имеет
вид
Разделив эту сумму на объем 
параллелепипеда, получаем искомую производную
в виде
Эта производная имеет вид
и
носит название градиента скалярной функции U.
Так как проекции действующей силы F на координатные
оси соответственно равны:
то
сила 
получается как
градиент от силовой функции U.
Описанную методику можно распространить и на случай
векторного поля; для этого вместо скаляра U
надо брать значения вектора поля в
соответствующей точке и множить на единичный вектор направления. Так как это
произведение может быть скалярным или векторным, то получаем два вида
производной — дивергенцию и ротацию.
Дивергенция определяется так:
где
S — площадь, а V — объем элемента..
Если — сила,
определяемая силовой функцией U, то
дивергенция вектора
.
В случае ротации
или в раскрытом виде, если 
:
или сокращенно
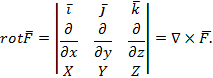
Можно показать, что условие существования силовой
функции для силы 
можно выразить
так:
Векторное поле, для которого ротация равняется нулю,
называется потенциальным.
Если рассматриваемые силы обладают силовыми функциями,
то геометрическое сложение сил можно заменить алгебраическим сложением
соответствующих силовых функций. Особенно это удобно, если рассматриваются
взаимодействия не между отдельными материальными точками, а между их системами.
Задачи такого вида решены в теории притяжения.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
