Главная
Тема 46. А.П.Котельников. Казанская школа математиков
А. П.
Котельников является представителем
Казанской школы математиков, стоящей в одном ряду с
Петербургской и Московской. Основателем этой школы был Н. И. Лобачевский (1792—1856), работа которого определила характер
всей школы, выделившейся своей оригинальностью: если Москва и Петербург в общем следовали западноевропейским классическим
образцам, сохраняя евклидово пространство, то Н. И. Лобачевский и его
последователи пошли своей дорогой, сосредоточив внимание на новых и необычных
образах.
Н. И. Лобачевский родился в Нижнем Новгороде в 1792 г.
В 1807 г. он поступил в Казани в недавно открытый университет, где его
руководителями были близкий к Гауссу математик М. Р. Бартельс
и астроном И. А. Литтров. По окончании университета
он получил степень кандидата. Его первой работой была «Теория эллиптического
движения небесных тел», а второй — «О разрешении алгебраических уравнений хm
— 1 = 0».
В 1816 г. он получает звание экстраординарного
профессора, а после отъезда Бартельса становится
ведущим математиком университета в назначается ординарным профессором кафедры чистой математики и кафедры
физики.
В области теоретической механики Н. И. Лобачевскому
принадлежит напечатанная в 1835 г. в «Ученых записках Московского университета
работа «Условные уравнения для движения и положения главных осей в твердой
системе», но начиная с 1826 г. он целиком обращается к своей основной работе в
области неевклидовой геометрии. Доклад о полученных
результатах (краткое изложение основ геометрии со строгим доказательством
теоремы о параллельных) был сделан им в Казанском университете в 1826 г. и не
встретил одобрения. Вопрос о том, какая геометрия действительно
существует в природе, по его мнению, мог быть решен только опытным путем при
помощи астрономических наблюдений. Он был глубоко прав в том отношении, что
полная история теоремы о параллельных немыслима без
привлечения астрономических исследований.
Прямоугольник был первой фигурой,
рассмотренной в геометрии; его построение требовало проведения параллельных
прямых, точки одной из которых находились постоянно на одинаковых расстояниях
от другой. Таким образом,
определение параллельных прямых как эквидистантных
было исходным. Это видно из того, что в астрономии в эпоху Евклида
«параллелями» назывались круги на небесной сфере, получаемые в сечении
плоскостями, перпендикулярными к оси Земли. Но эти так называемые малые круги
нельзя было отождествить с большими кругами, которые на сфере играли роль
прямых линий в плоской геометрии. Таким образом, Евклид
понял, что эквидистантность не может служить
определением параллельных прямых; поэтому в «Началах» он дал определение
прямой, параллельной данным, как не пересекающей ее, сколь далеко она ни
продолжалась бы. Неудобство такого определения (нельзя определять объект
свойством, которого он не имеет) чувствовали приверженцы строгой логики и,
безусловно, сам Евклид, так как он добавил два постулата (4-й и 5-й).
Определение параллельной и эти постулаты составили «пятно» на геометрии
Евклида, которое греческие, арабские и западноевропейские математики старались
безуспешно снять, пытаясь «доказать» истинность постулатов Евклида.
В самом конце XVIII в. Гаусс, будучи еще студентом
Геттингенского университета, вместе с Больяи-старшим
обсуждал возможность существования другой геометрии, кроме
Евклидовой. Работу Больяи, которая вышла в 1831 г. на
шесть лет позже первого труда Лобачевского, выполнил его сын.
В 1826 г. Н. И. Лобачевский был назначен ректором
Казанского университета. Главой русской математики в то время был М. В.
Остроградский, который на присланную ему в 1832 г. работу Н. И. Лобачевского «О
началах геометрии» прислал отрицательный отзыв.
В 1842 г. по предложению Гаусса Н. И. Лобачевский был избран членом-корреспондентом Геттингенского
научного общества, а среди русских ученых профессор П. И. Котельников (1809—1879) произнес речь, в которой он отметил,
что изумительный труд Н. И. Лобачевского «О началах геометрии» рано или поздно
найдет своих ценителей.
П. И. Котельников был с 1838 г. профессором Казанского
университета по кафедре прикладной механики и одновременно
читал курсы теории функций комплексного переменного основ геометрии и
векторного исчисления. С 1829 по 1862 г. он был деканом физико- математического
факультета и одним из немногих, оценивших геометрические открытия Н. И.
Лобачевского, в то время как гениальный творец неевклидовой геометрии не
получил общего признания.
А. П. Котельников родился 8 октября 1865 г. в Казани.
После окончания в 1883 г. гимназии с серебряной медалью А. П. Котельников
колеблется в выборе между техникой и математикой: сначала он поступает в
Петербургский технологический институт, но уже в следующем году переводится на
физико-математический факультет Казанского университета. В 1888 г. он защищает
кандидатскую диссертацию «О давлении жидкой струи на клин», которое он
определяет по методу Кирхгоффа. Эта диссертация выросла из дипломной работы,
которую он выполнил под руководством профессора И. С. Громеки.
После окончания университета он два года преподает
математику в женской гимназии, а затем остается при университете для подготовки
к профессорскому званию. Атмосфера в университете, в котором ему пришлось
работать, была пропитана идеями Лобачевского. Профессорский состав университета
представляли: Ф. М. Суворов, диссертации которого:
магистерская «О характеристиках систем трех измерений» и докторская «Об
изображении воображаемых точек и воображаемых прямых на плоскости» — были тесно
связаны с работами по неевклидовой геометрии; А. В. Васильев — ученый,
работавший во многих областях математики и пропагандист многих новых идей
математики в России, редактор первого Собрания сочинений Н. И. Лобачевского и
автор его биографии; Г. Н. Шебуев, читавший в
Казани основные курсы по теоретической механике с 1879 по 1888 г., а затем
переехавший в Москву, где он преподавал в Константиновском Межевом институте.
Ему принадлежит работа «Приложения теории кватернионов к механике подобно и
однородно изменяемых систем», изданная в 1893 г. в Казани; в Москве в 1898—1899
гг. он напечатал в «Памятных книжках Константиновского Межевого института»
очерк векторного исчисления и теории кватернионов.
В этом же направлении начинает работать и А. П.
Котельников. В 1893 г. он был утвержден приват-доцентом Казанского
университета, где читает курс графической статики и ведет практические
упражнения по теоретической механике. С этого же года он начинает работу над
своей магистерской диссертацией «Винтовое исчисление и некоторые его применения
к геометрии и механике», которую он защитил в 1896 г.
Пуансо показал, что любую систему сил в пространстве можно
заменить одной силой R — главным
вектором, приложенным к некоторой точке, и парой, момент которой равняется
сумме моментов всех сил системы относительно этой точки. Равным образом, в
кинематике Шаль показал, что любое перемещение твердого тела в пространстве
можно получить в результате сложения поступательного движения, определяемого
скоростью v некоторой точки тела и угловой скоростью Ω вращения вокруг
оси, проходящей через эту точку. Наиболее удобен выбор такой точки тогда, когда
векторы силы и момента пары в статике или скоростей v и Ω бесконечно малого перемещения твердого тела в кинематике
направлены по одной прямой; таким образом, получается силовой винт, или динама, в статике и кинематический винт в теории движения
твердого тела. Прямая линия, представляющая геометрическое место точек,
обладающих таким свойством, носит название центральной оси динамы,
или кинематического винта.
Пусть точка О представляет начало координат. Скорость этой точки 
, а угловая скорость вращения 
.
Пусть координаты точки центральной оси x, у, z. Скорость этой точки
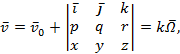
где
k — некоторый коэффициент.
Уравнения центральной оси имеют вид
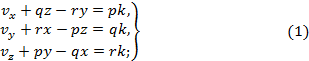
Коэффициент
k — так называемый параметр винта —
представляет отношение скоростей v/Ω для кинематического винта или
отношение наименьшего момента к главному вектору для силового винта (динама). Уравнения (1) представляют собой уравнения
центральной оси, а уравнение (2) определяет величину параметра. Пять координат
(четыре для прямой, пятая для параметра) определяют геометрический винт как для силового, так и для кинематического винта. Для
полного представления остается только добавить вектор угловой скорости Ω в
случае кинематического винта или главный вектор R для силового винта (динамы).
Пять координат, определяемых уравнениями (1) и (2),
вполне определяют геометрический винт. Однако удобнее определять его шестью
однородными координатами, которые представляют векторы скоростей v и Ω в кинематике или главный
вектор и главный момент в статике. Абсолютные величины
v и Ω могут быть какими угодно; существенным является лишь их отношение, т.
е. параметр k.
Английский математик Вильям Клиффорд ввел понятие о
новом виде комплексных чисел. Кроме обычных комплексных чисел
где
i2 = — 1, называемых
гиперболическими, он ввел еще два новых вида:
где
ω2 = +1 — так называемые эллиптические числа, и
где
ω2 = 0 — параболические числа.
А. П. Котельников совокупность двух векторов 
и 
назвал
бивектором и, следуя Клиффорду, определял его в виде
где
ω2 = 0. При помощи этого обозначения он установил правила действия
над винтами, продолжив работу ирландского математика Роберта Болла (1840—1913) в труде «Теория
винтов».
Пусть даны два винта, выраженные в однородных, или плюккеровских, координатах:
Суммой винтов α + β называется винт у, однородные координаты которого равны суммам
соответствующих координат складываемых винтов:
Центральная ось и параметр получающегося винта находятся
по уравнениям (1) и (2), в которых вместо vx, vy, vz,
p, q, r стоят суммы соответствующих
координат. Практическое решение этой задачи было дано Боллом
при помощи линейчатой поверхности» образующие которой параллельны одной плоскости, так называемого
цилиндроида Болла.
Рассмотрим общий случай умножения двух бивекторов.
Пусть даны два бивектора
где
ω — комплексная единица, удовлетворяющая условию ω2 = 0, а 
— единичные
векторы координатных осей, перемножающиеся по
правилам, установленным Гамильтоном.
Это произведение можно представить и так:
где
A и В - кватернионы:
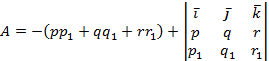
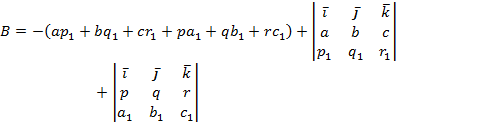
Выражение A + Bω Клиффорд назвал бикватернионом;
таким образом, произведение двух бивекторов дает бикватернион,
аналогично тому, что произведение двух векторов дает кватернион,
распределяющийся на две части — скалярное и векторное
произведения
векторов.
Рассмотренные выше оикватернионы могут
представить движение в евклидовом пространстве. Если положить ω2=+1
или ω2=-1, то можно показать, что соответствующие бикватернионы представляют движение в эллиптическом
пространстве (сферическая геометрия) при ω2=+1 ив
гиперболическом пространстве (геометрия Лобачевского) при ю2
= —1. В остальных частях диссертации А. П. Котельников рассматривает операции
над бикватернионами в евклидовом пространстве, а
также приложения их в геометрии и механике.
Дальнейшая деятельность А. П. Котельникова заключалась
в распространении положений его магистерской диссертации на самый общий случай,
покрывающий как эллиптическое, так и гиперболическое пространства. Это
составило предмет его докторской диссертации «Проективная теория векторов»,
защищенной в 1899 г. За эту диссертацию Ученый совет университета удостоил А.
П. Котельникова степени доктора прикладной математики (механики), а затем и
доктора чистой математики.
В основе всей механики лежит закон параллелограмма,
которому подчиняются и силы, и скорости. Но параллельные
прямые существуют только в евклидовом пространстве; в эллиптическом
пространстве (на сфере) их нет совершенно, а в пространстве Лобачевского задача
о проведении прямой, параллельной данной, не допускает единственного решения.
Таким образом, возникает вопрос, каким образом нужно сформулировать закон
параллелограмма, если рассматриваемое пространство не является евклидовым.
Закон параллелограмма можно выражать в двух формах.
Во-первых, сумма двух векторов 
и 
выражается
диагональю параллелограмма, построенного на обоих векторах. Во-вторых, вместо
параллелограмма можно взять треугольник ОВС
и сформулировать для него теорему синусов
В неевклидовом пространстве можно пользоваться только
второй формой, тем более что теорема синусов справедлива не только в
прямолинейной, но и в сферической тригонометрии; разница лишь в том, что вместо
длин сторон треугольника нужно брать их синусы. Это указывает
еще на одно необходимое изменение: так как прямые являются геодезическими
линиями только на плоскости, то нужно отказаться от прямолинейности сторон.
Поэтому вектор будем рассматривать как упорядоченную комбинацию двух его точек 
, 
, 
, не обращая внимания на вид линии, соединяющей эти
точки. Определение действия сложения двух векторов
должно
удовлетворять следующим условиям:
1. Необходимы распределительный, сочетательный и
переместительный законы.
2. Если складываемые векторы находятся на одной
прямой, то результат сложения выражается их алгебраической суммой.
3. Если длины складываемых векторов одинаковы и они
образуют между собой угол 2х, то
вектор-сумма пойдет по направлению, образующему со складываемыми векторами
одинаковые углы х. При этом, если
«длины» складываемых векторов равны р, то «длина» R
вектора-суммы выражается формулой
где
f(x) —пока еще неизвестная функция
угла х.
Для определения свойств этой функции воспользуемся
следующим Построением.
Пусть из точки О (рис. 41) в одной плоскости проведены четыре одинаковых
прямых ОА, ОА/, ОВ, ОВ/ и пусть углы АОВ и А/ОВ/ равны каждый 2у. Пусть ОС и ОС/ — биссектрисы этих углов
и угол между ними равен 2х. Проводим биссектрису
OD угла СОС/. Пусть р — длина каждого вектора ОА, ОВ, ОА/, ОВ/ требуется определить
вектор-сумму этих четырех векторов.
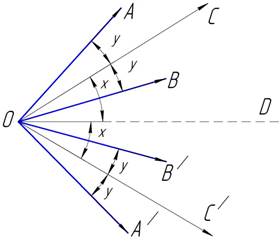
Рис 41
Если сочетательный закон действителен, то можно
произвольно комбинировать складываемые векторы.
Сначала сложим векторы ОА и ОА/: их
сумма имеет направление прямой OD и
равна 
. Сумма ОВ и
ОВ/ тоже пойдет по OD и будет иметь величину 
. Поскольку полученные суммы лежат на одной прямой, то
окончательная сумма всех четырех векторов тоже имеет направление этой прямой и
равна их алгебраической сумме
Эту же сумму можно получить, если сложить сначала
векторы ОА и ОВ, а затем ОА/
и ОВ/. Сумма первых векторов
пойдет по ОС и равна 2pf(y), а сумма двух вторых векторов,
равная тоже 2pf(y), пойдет по ОС. Так как OD является биссектрисой угла СОС/
у то окончательная сумма тоже пойдет по этой прямой и равна
Теперь для определения вида f имеем равенство
или
.
Если использовать формулу тригонометрии
то
в качестве функции, удовлетворяющей условию (а), можно взять функцию coskx, где k может иметь любое значение. Если k = 1, то f(х) = cosx и
сумма двух векторов, равных р и
образующих между собой угол 2х, равна
2рcosα, т. е. получаем теорему
параллелограмма векторов в евклидовом пространстве. Если k> 1, то получаем закон сложения в эллиптическом пространстве, а
при k < 1 — в гиперболическом.
Если теорема доказана для сложения двух равных сил, то
нетрудно провести доказательство и для неравных сил.
Покажем, как изменится параллелограмм, если
складываемые векторы расположены в эллиптическом пространстве, в котором
действуют законы сферической геометрии.
Пусть два вектора ОА
и ОВ приложены в одной точке О (рис. 42). Через три точки О, A, В проводим сферу; точку приложения
О берем в качестве полюса и проводим
для него большой круг (экватор) CDC/.
Через точки А и В — концы векторов — проводим меридианы ОАС/ и OBD до
пересечения их экватором. Затем соединяем большими кругами точки А и D,
В и С/, находим точку Е их пересечения; она и определит вектор
ОЕ — сумму ОА и ОВ.
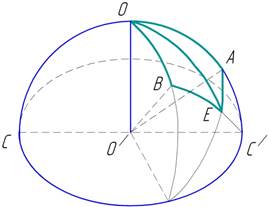
Рис. 42
Если радиус сделать равным бесконечности, то
поверхность полусферы обратится в плоскость, проходящую через точку О, а центр О/ экваториальной
окружности и сама окружность уйдут в бесконечность. Дуги ОА и ОВ обратятся в
прямые линии, расположенные в плоскости ОАВ.
Дуга AD, которая теперь тоже станет
прямой, пересечет меридиан OBD в
бесконечно удаленной точке, т. е. станет параллельной прямой ОВ.
Точно так же дуга ВС
обратится в прямую, параллельную ОА;
поэтому четырехугольник ОАЕВ
представляет параллелограмм, а диагональ ОЕ
этого параллелограмма и будет искомой
суммой векторов ОА и ОВ.
Пользуясь законом двойственности проективной
геометрии, можно еще дальше обобщить понятие о векторе. Так как некоторую точку
пространства можно привести в соответствие с любой плоскостью при помощи
определенного закона соответствий (что делается при построении диаграммы
Кремоны), то любое соотношение, установленное для ряда точек, остается
справедливым и в том случае, когда вместо отдельных точек подставлены
плоскости, соответствующие этим точкам.
В курсах проективной геометрии очень часто делят
страницы пополам: на одной половине доказывается теорема для системы точек, а
на другой — та же теорема, в формулировке которой точки заменены
соответствующими им элементами (в пространстве трех измерений плоскостями, а на
плоскости — прямыми).
В качестве примера таких «двойственных теорем» можно
привести самые простые; например, две точки на плоскости определяют прямую,
проходящую через эти точки; равным образом две прямые на плоскости определяют
точку, в которой они пересекаются, и т. д.
Исходя из этих соображений, А. П. Котельников ввел
новые типы векторов. Так, например, поскольку точку можно заменить плоскостью,
то можно рассматривать вектор, образованный двумя плоскостями. Так как в
пространстве двойственным образом для прямой будет тоже прямая (достаточно
напомнить соответствующее свойство в диаграмме Кремоны), то линии действия
вектора, определяемого двумя точками, при замене этих точек плоскостями будет
соответствовать по закону двойственности прямая пересечения этих плоскостей.
Полученный таким образом преобразованный вектор А. П. Котельников назвал
ротором. Можно рассматривать векторы, образованные точкой и плоскостью, так
называемые «мутовки»; это будет нечто аналогичное динаме, которая определяется
силой и парой. Такие проективные соответствия ясно показывают сущность связей,
которые имеются между векторами сил и угловых скоростей (и те, и другие
складываются по закону параллелограмма), между динамическим (силовым) и
кинематическим винтами, исследованию которых была посвящена первая работа А. П.
Котельникова.
После защиты диссертации А. П. Котельников избирается
по конкурсу заведующим кафедрой механики в открытом в 1898 г. Киевском
политехническом институте. На основании прочитанных им лекций он пишет курс
механики, или, вернее, два курса: «Механика», которая соответствует материалу,
читавшемуся тогда на первом курсе высших технических учебных заведений (в
Московском высшем техническом училище этот курс носил название «Теоретическая
механика»), и «Аналитическая механика»» содержавшая материал читавшийся на
втором курсе. В этих курсах следует отметить применение векторной алгебры,
правда, еще не совсем полное, так как для скалярного произведения двух векторов
А. П. Котельников пользуется обычным в то время названием геометрического.
В 1904 г. А. П. Котельников возвращается в Казань, где
он получает кафедру математики в Казанском университете, которую он занимает до
1914 г. К этому времени относится написанный им «Курс аналитической геометрия»,
в котором тоже применяется векторное исчисление.
В 1914 г. А. П. Котельников начинает работать на
кафедре математики Киевского университета. Он читает лекции по высшей
математике для студентов естественного отделения, а также специальные курсы
(начертательную дифференциальную, проективную и неевклидову геометрию). С 1920
по 1924 г. он читает курс механики в Киевском политехническом институте, а
также преподает математику на Высших женских курсах.
В 1924 г. А. П. Котельников переезжает в Москву, где
начинает читать курс теоретической механики в Московском высшем техническом
училище.
В эти годы шла перестройка педагогической работы на
кафедре теоретической механики. Начиная с 1921 г. организуются групповые
занятия по основным предметам, в том числе й по теоретической механике, и
приглашается большое число новых преподавателей. Затем пересматривается
программа курса механики: выбрасывается теория планетных движений и заменяется
теорией колебаний; устраняется деление на теоретическую и аналитическую
механику и устанавливается единый курс, читающийся два года; на двух первых
семестрах читается статика и полный курс кинематики, в который включается
материал, требовавший знания высшей математики и читавшийся ранее в
«Аналитической механике».
Читавшееся на первом курсе краткое введение в динамику
устраняется и передается на второй курс, где полностью в течение двух семестров
читается весь курс динамики. Программу последнего курса тоже приходится
перестраивать: вследствие необходимости согласования с чтением курса высшей
математики перераспределяется учебный материал механики, т. е. вместо обычного
деления на динамику точки (третий семестр) и динамику системы (четвертый
семестр) на третьем семестре читаются общие теоремы динамики без разделения на
динамику точки и динамику системы, а на четвертом семестре излагаются главным
образом задачи интегрирования дифференциальных уравнений динамики тоже без
разделения на динамику точки и системы.
Кафедру механики на механическом факультете
Московского высшего технического училища А. П. Котельников занимал двадцать
лет.
Кроме МВТУ А. П. Котельников вел курсы теоретической
механики и в других московских вузах: в институте инженеров транспорта, в
химико-технологическом институте, в Московском лесотехническом институте, в
Московском энергетическом институте, а также и в бывшем Комиссаровском, а потом
Ломоносовском институте до его преобразования в Московский вечерний рабочий
институт. Кроме этого, в 1930—1932 гг. он был одним из активных организаторов
Высших инженерно-педагогических курсов, на которых он читал теоретическую
механику.
Двадцатые годы ознаменовались еще одной реформой в
изложении механики — введением векторного исчисления. Инициатором этого направления
в московских вузах был профессор Московского университета Н. Н. Бухгольц,
начавший читать лекции по механике в векторном изложении с самого начала 20-х
годов, когда он заменил в университете Н. Е. Жуковского. В МВТУ это произошло
несколько позднее, примерно около 1925 г., причем большую роль в этом деле
играл профессор математики на энергетическом факультете МВТУ Я. Н. Шпильрейн.
Его инициативу поддержали А. И. Некрасов и А. П. Котельников, который уже
применял такое изложение в Киевском университете.
С 1930 г. А. П. Котельников получает возможность
уделять гораздо больше времени чисто научной работе. К 20-м годам относится его
работа «Принцип относительности и геометрия Лобачевского», опубликованная в
1927 г. в сборнике, посвященном памяти Н. И. Лобачевского, но задуманная ранее:
он доказывал ее в 1923 г. на заседании Московского математического и в 1926 г.
на заседании Казанского физико-математического обществ.
В 1927 г. А. П. Котельников выступил с докладом о
точках Бурместера, относящихся к кинематике плоских механизмов, и в том же году
в «Трудах МММИ им. Баумана» (тогдашнее название МВТУ) опубликовал «Заметку о
графической динамике».
С 1930 г. А. П. Котельников начинает работать в
Центральном аэро-гидродинамическом институте, где он занимается редактированием
Полного собрания сочинений Н. Е, Жуковского. При этом он не ограничивается
редактированием уже имеющегося текста, а занимается восстановлением работ Н. Е.
Жуковского, которые еще не были закончены. Так, им была восстановлена работа
«Действие волнующейся жидкости малой глубины на плавающие на ее поверхности
тела» по черновикам Н. Е. Жуковского, в значительной части состоявшим только из
одних математических вычислений без каких бы то ни было пояснений. К этой
работе он добавил приложение, дополняющее результаты, полученные Н. Е.
Жуковским, а также провел специальное исследование давления жидкости на тело,
качающееся на волнах; последняя задача не была решена Н. Е. Жуковским, но
данные им формулы позволили А. П. Котельникову решить ее до конца.
А. П. Котельников принял также участие в работе над
изданием Собрания сочинений Н. И. Лобачевского, для которого им было написано
несколько статей, в частности «Некоторые применения идей Лобачевского в
механике и физике».
А. П. Котельников является одним из ведущих механиков
XX в., когда неевклидова геометрия и новые пространственные образы играют в
механике и в физике не меньшую роль, чем основные понятия классического
анализа.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
