Главная
Тема 14. Механика
Галилея
Галилео Галилей, сын Винченцо Галилея,
происходившего из обедневшего патрицианского рода, родился во Флоренции 15 февраля
1564 г. Флоренция в его время уже не была тем свободным городом, центром
культурной жизни Италии и вообще Западной Европы, который дал великого поэта
Данте Алигьери (1265—1321), архитектора Филиппо
Брунеллески (1377—1446), живописца Леонардо да Винчи (1452—1519), политика Никколо Маккьявелли (1462—1527)
и, наконец, скульптора Микеланджело Буонаротти (1475—1564)
—свидетелей гибели свободы Флоренции и наступления феодально-католической
реакции в Италии.
Эпоха
Возрождения XIV—XV вв. была временем наивысшего расцвета городской жизни и
культуры Италии. Близкое соседство с Византией, для которой в XIV в. росла
угроза турецкого завоевания, способствовало бегству в Италию греческой
интеллигенции, познакомившей итальянцев с греческим языком и античными классиками.
В Италии стали развиваться литература и искусство, достигшие небывалой высоты.
Средневековая схоластика заменялась гуманизмом, идеалом которого являлся
гармонично развитый человек, далекий от аскетизма и умеющий красиво жить и
свободно мыслить.
Вместе с тем
нельзя не указать и на некоторые отрицательные стороны итальянского гуманизма.
Крушение схоластического мировоззрения способствовало, как это характерно для
переходных эпох, развитию мистических учений, которые особенно ярко проявились
в XVI в.
Появилось
также новое учение — философия Платона, которая сильно привилась в итальянских
городах и больше всего во Флоренции. Наряду с развитием филологии, особенно
классической, физико-математические науки не дали ни одного выдающегося
представителя; новая астрономия Региомонтана, Пурбаха и Коперника создавалась вне Италии.
Развитие самостоятельности итальянских городов наряду с положительными
имело и отрицательные качества: в то время как на Пиренейском полуострове, в
Англии и во Франции, а также я на востоке Европы — в Чехии, Польше, Венгрии и
России — складывались национальные государства, Италия представляла собой ряд
разрозненных городских республик и сделалась ареной борьбы между Испанией и
Францией в первой половине XVI в. Победительницей в этой борьбе
оказалась Испания, подчинившая прямо или косвенно почти всю Италию, за
исключением лишь Венеции. В 1527 г. Рим был взят и разграблен ландскнехтами
Карла V, а после этого — и Флоренция, где городская республика была уничтожена,
сделалась столицей тосканских герцогов из рода Медичи; эпоха Возрождения пришла
к концу и сменилась феодальной реакцией.
В такой
исторической эпохе развивалась научная деятельность Галилео Галилея (1564—1642). С 1589 по 1592 г. он работал
преподавателем в Пизанском университете, в котором получил образование.
Положение его в материальном отношении было очень тяжелым, и он переехал в
Венецию, где стал профессором Падуанского
университета. Годы его пребывания в Венеции (1592—1610) были наиболее
счастливым временем его жизни: он приобрел большое количество друзей (недаром в
его основных сочинениях «Диалоги о двух системах мира» и «Рассуждения о двух
новых науках» действие происходит в Венеции, где закончилось формирование
научного облика Галилея).
В 1609 г. в
жизни Галилея произошло важное событие; услышав об изобретении в Голландии
зрительной трубы, он сконструировал оптический прибор (телескоп), который
демонстрировался венецианским властям и получил их одобрение. Первоначально
этот прибор предназначался для земных наблюдений на далеких расстояниях, но в
январе 1610 г. Галилей направил его на небо и увидел там множество звезд, не
видимых невооруженным глазом; при этом он открыл структуру Млечного пути и
обнаружил у Юпитера наличие четырех спутников. Результаты этих наблюдений,
опубликованных в «Звездном Вестнике», произвели фурор в ученом мире.
О своих
дальнейших наблюдениях (наличие фаз у Венеры и особая форма Сатурна) он сообщил
в зашифрованном виде. Во второй половине 1610 г. спутников Юпитера обнаружили
также астрономы-иезуиты Римской коллегии, и Галилей получил общее признание.
Несмотря на удерживание со стороны венецианских друзей, он перешел на службу к
тосканскому гердогу Козимо
Медичи в качестве придворного философа и математика.
В последний
период его деятельности (l610—1642) Основной задачей, кроме борьбы за систему
Коперника, было подведение итогов своих исследований о
движении свободно падающих и брошенных тяжелых тел.
Первая задача
была им решена недостаточно удачно. Во-первых, он не понял, каким образом
Коперник представлял себе движение Земли; он не знал разницы между настоящим
вращением тела вокруг неподвижной оси и круговым поступательным движением;
во-вторых, описанная им в «Диалогах о двух системах мира» система мира, по
существу, воспроизводила уже отброшенную систему Аристарха Самосского.
Хотя Галилей и
считал, что «книга природы написана математическими знаками», но на практике он
далеко не всегда пользовался математикой, так как предполагал, что законы
природы должны быть выражены очень просто. В этом отношении знаменательно, что
Галилей был дружен с Кеплером, находился с ним в переписке и не мог не знать об
его первом законе, по которому планеты движутся по эллипсам. Далее Галилей
полагал возможным доказать правильность системы Коперника явлением приливов,
как это делал за две тысячи лет до него Селевк
Вавилонский. Наконец (и это самое главное), из всей теории Коперника Галилей
лучше всего усвоил наиболее слабую ее часть, а именно: понятие о космической
инерции.
Самым ценным у
Галилея была не его астрономическая деятельность, а то, что он первым заложил
основы новой динамики; важна не его критика системы Птолемея, а нанесенный им
удар по динамике Аристотеля. Всем известен его «Диалог о двух главнейших
системах мира» (Птолемеевой и Коперниковой), но до. конца XIX в. мало кто обращал
внимание на его «Беседы и математические доказательства, касающиеся двух новых
наук». Этими двумя науками были сопротивление материалов и динамика; поэтому
Галилея можно с полным правом назвать отцом двух этих новых отраслей физико-математических
наук.
Рассмотрим
динамику Галилея, которую он назвал «Наукой о движении относительно места» (movimenti lоcali);
зная классификацию видов движения в «Диалектике природы», можно хорошо понять
значение этого термина.
Сочинение
«Беседы и математические доказательства, касающиеся двух новых начал»
распадается на три части: о равномерном движении, о равномерно ускоренном
движении и о принужденном движении брошенных тел.
Первая часть
представляет интерес как последовательный этап в развитии понятия о скорости. В
античной механике термина «скорость» еще не было. Имелись в виду более или
менее скорые движения, равноскорые с самим собой, но
скорость как особая величина не рассматривалась. У Галилея термин «скорость»
имеется» но он не дает определения скорости или способа ее измерения, а говорит
только об отношениях двух скоростей. Если два тела движутся равномерно, то
отношение скоростей их равняется отношению пройденных расстояний, умноженному
на обратное отношение времен движения.
Во второй
части («О равномерно ускоренном движении») понятие скорости расширяется: если в
первой части Галилей следует античной терминологии, то здесь употребляемые им
выражения являются в основном теми, которыми пользовался автор XIV в. Николь Оресм.
Николь Оресм был наставником французского короля Карла V
(1337—1380) и окончил жизнь епископом Лизье. Он
принадлежит к числу средневековых ученых, ставших известными лишь в недавнее
время и вызвавших немалый интерес историков науки. Его считали предшественником
Коперника, поскольку он предполагал о возможности движения Земли; в
действительности он считал, что центр тяжести Земли должен совпадать с центром
мира, и если на поверхности Земли происходят какие-либо передвижения,
изменявшие положение центра ее тяжести, то Земля тоже должна передвигаться,
чтобы ее центр совпадал с центром мира.
Он был
противником астрологии и доказывал ее ненадежность тем, что вследствие
несоизмеримости периодов движения небесных тел невозможны точные повторения их
соединений, квадратур, противостояний и т. д., на основании которых делались
предсказания. Эти повторения были бы возможны только в том случае, если бы
отношения периодов движений небесных тел выражались рациональными числами. Но
если периоды планетных движений абсолютно независимы между собой, то
вероятность рациональных их отношений равна нулю, так как мощность множества
рациональных чисел (счетное множество) бесконечно мала по сравнению с мощностью
континуума, которым измеряется множество действительных чисел.
Оресма считали изобретателем аналитической геометрии,
поскольку он пользовался геометрическим изображением изменения переменных
величин. Однако соответствующая теория, изложенная Оресмом
в сочинении «De latitudinibus
formarum» (заглавие переводят как «О протяжениях
форм», или «О конфигурации качеств»), имела большое значение для исследований
Галилея; более того, терминология Оресма и до сих пор
в какой-то мере сохраняется в современной науке.
Пусть значение
какой-либо величины остается постоянным с течением времени. Если по горизонтали
отложить последовательные моменты времени, то концы полученных отрезков
окажутся на прямой, параллельной той горизонтали, по которой отложено время.
Такое изменение Оресм называл униформным
(uniformis), т. е. равномерным. Если исследуемая
величина представляет скорость, то график последовательности отложенных
отрезков является прямоугольником,
площадь которого изображает графически расстояние s, пройденное за время t
в равномерном движении со скоростью v
(рис. 30).
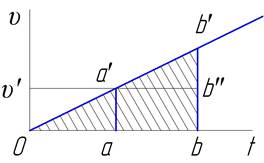
Рис. 30
Если концы
отложенных отрезков лежат на некоторой кривой, то изменение называется
дифформным (difformis); если эта кривая-прямая линия, идущая из начальной точки
отсчета, то соответствующее изменение называется равномерно-неравномерным
(uniformiter difformis); в этом случае пройденное расстояние выражается
площадью треугольника Obb′ или
прямоугольника Oa'bb":
![]()
т. е. оно равняется расстоянию, пройденному за то же
время t в равномерном движении со скоростью, изображаемой отрезком аа′ соответствующей моменту
времени, изображаемому отрезком Оа = ![]() Оb. Это
построение и явилось исходным для теории переменного движения Известно, что
движение свободно падающего тела ускоряется в процессе падения, но закон
соответствующего изменения скорости долго оставался неизвестным; считали, что
стремление тела к своему естественному месту увеличивается в зависимости от
приближения падающего тела к этому месту. Приступая к определению этого закона,
Галилей писал:
Оb. Это
построение и явилось исходным для теории переменного движения Известно, что
движение свободно падающего тела ускоряется в процессе падения, но закон
соответствующего изменения скорости долго оставался неизвестным; считали, что
стремление тела к своему естественному месту увеличивается в зависимости от
приближения падающего тела к этому месту. Приступая к определению этого закона,
Галилей писал:
«Когда я замечаю,
что камень, выведенный из состояния покоя и падающий со значительной высоты,
приобретает все новое и новое приращение скорости, не должен ли я думать, что
подобное приращение происходит в самой простой и ясной для всякого форме? Если
мы внимательно всмотримся в дело, то найдем, что нет приращения более простого,
чем происходящее всегда равномерно».
Для Галилея
оставался невыясненным вопрос, будет ли это изменение пропорциональным
пройденному пути или времени. После некоторых колебаний он склонился к мнению,
что пропорциональность пройденному пути следует отбросить, и определил, что
свободное падение есть равноускоренное движение, в котором в равные промежутки
времени получаются и равные приращения скорости.
В этом
отношении интересна разница между взглядами Галилея и Кеплера. Круговое
движение планет у Галилея Кеплер заменил более сложным движением по эллипсам; в
случае свободного падения он нашел, что скорость падения возрастает
пропорционально квадратному корню из пройденного пути.
Галилей
сначала теоретически, а затем и опытным путем установил, что пройденные пути за
первую, вторую, третью и т. д. секунды возрастают пропорционально ряду
последовательных нечетных чисел: 1:3:5 и т. д. Затем он вывел закон изменения
скорости пропорционально времени:
![]()
и пройденного пути пропорционально квадрату времени
![]()
Соответствующие
измерения Галилей производил на наклонных плоскостях, учитывая данные Иорданом
Неморарием изменения тяжести в зависимости от положения.
Динамические
воззрения Галилея легко обнаруживаются из следующих слов:
«Рассматривая
тело, брошенное вверх, я нахожу, что сила, давшая ему первоначальное движение,
постепенно уменьшается; сила эта поднимает тело до тех пор, пока она
превосходит противодействующую силу тяжести; но как только эти силы
уравновешиваются, тело перестает подниматься и переходит в состояние покоя. При
этом первоначально сообщенный импульс уничтожается не чем иным, как постепенным
погашением первоначального излишка его над весом тела, каковой заставляет тело двигаться
вверх. Так как уменьшение этого импульса продолжается,
следствием чего является перевес силы тяжести, то начинается обратное движение,
или падение тела, происходящее вначале медленно, вследствие противодействия
первой силы, значительная часть которой еще сохраняется в теле; но так как эта
последняя постепенно уменьшается и все в большей степени преодолевается силой
тяжести, то отсюда и возникло постепенное ускорение движения».
Галилей
считал, что сила, двигавшая камень первоначально вверх, исчезает:
«Факт покоя,
предшествующего падению камня и продолжающегося долгое или короткое время, или
же одно лишь мгновение, не имеет никакого значения, так как камень не падает до
тех пор, пока находится под действием силы, противодействующей его тяжести и
достаточной для того, чтобы удержать его в покое».
Отсюда
становится совершенно ясным, что падение камня, которое Аристотель считал
естественным, совершающимся без приложения какой-либо силы, в действительности
является насильственным, происходящим под действием силы тяжести. Это была
«первая брешь в стенах крепости Аристотелевой динамики». Кроме того, Галилей
определил закон движения, совершающегося под действием постоянной силы; сейчас
это соответствует тому, что постоянная сила производит постоянное ускорение, но
во времена Галилея вплоть до самого XIX в. термин «ускорение» был неизвестен.
Этим
исследования Галилея не заканчиваются; он решает стоящую в
начале XVI в. баллистическую задачу — определяет траекторию тела,
брошенного под углом к горизонту; при помощи сложения движений он показывает,
что при отсутствии сопротивления воздуха эта траектория была бы параболой.
Первым,
оценившим громадное значение Галилея в деле создания новой динамики, был Эрнст
Мах в своей книге «Die Mechanic in ihrer Entwicklung» (1883). В дальнейшем
слава Галилея как механика распространялась очень широко. Ему стали приписывать
не только открытие второго закона Ньютона, на что, как
видно, на предыдущего, он имел некоторое право, но
даже и открытие пёрвого закона. Подробное исследование произведений Галилея
показывает, что закон инерции он знал только в той форме, в какой он имеется у
Коперника, — в форме закона космической инерции; движение тела, на которое не
действуют силы, является равномерным движением по окружности.
Посмотрим, как
Галилей показывал несостоятельность некоторых возражений, приводимых против
вращения Земли. В просторном помещении под палубой корабля
находился сосуд с истекающей из него водой и с плавающими рыбками, летающие
мухи, бабочки и др. Если корабль движется равномерно и без качки в ту или
другую сторону, то все явления внутри этого помещения происходят совершенно так
же, как и в случае, когда корабль стоит неподвижно. При использовании
этого для доказательства так называемого Галилеева
принципа относительности необходимо учитывать, что равномерное движение корабля
без изменения курса совершается не по прямой линии, а по окружности большого
круга.
Можно привести
и более сильное доказательство в пользу того, что закон инерции у Галилея
понимался в смысле космической инерции. В «Диалоге о двух главнейших системах
мира» утверждается, что мир есть тело, в высшей степени
совершенное, и что в отношениях его частей должен господствовать
наивысший и наисовершеннейший порядок.
Установив
такое начало, из него можно непосредственно сделать вывод, что если тела,
составляющие Вселенную, должны по природе своей обладать движением, то
невозможно, чтобы движения их были прямолинейными и вообще какими бы то ни
было, кроме как круговыми. То, что движется прямолинейным
движением, меняет место и все больше удаляется от своей исходной точки; если
такое движение ему естественно присуще, то оно с самого начала не находилось на
своем естественном месте, значит, части Вселенной не расположены в совершенном
порядке; стало быть, невозможно допустить, чтобы им, как таковым, по природе
было свойственно менять места, т. е. двигаться прямолинейно.
Кроме того,
так как прямолинейное движение по своей природе бесконечно, ибо прямая линия
бесконечна и неопределенна, то невозможно, чтобы что-нибудь, движущееся от
природы, обладало свойством движения по прямой линии, т. е. к цели, достигнуть
которую невозможно. Если бы кто-нибудь стал утверждать, что природа произвольно
намечает некоторые пределы и вкладывает в свои естественные тела естественные побуждения
двигаться к этим пределам, то это подходит для мифа о том, что получилось из
первичного хаоса. Для приведения его в порядок природа очень удачно
воспользовалась прямолинейными движениями, которые пригодны для того, чтобы
ввести должный порядок в беспорядочные отношения.
Но после того
как достигнуто наилучшее распределение и размещение, невозможно, чтобы в телах
оставалась естественная склонность к прямолинейному движению, в результате
которого получились бы только отклонения от надлежащего и естественного места.
Прямолинейное движение может доставлять материал для сооружения; но раз
последнее готово, то оно или остается неподвижным, идо если и обладает
движением, то только круговым.
Приведенный
текст не оставляет никакого сомнения в том, что во всяком случае в год
окончания «Диалога о двух главнейших системах мира» (1630) Галилей полностью
придерживался идей Коперника о законе космической инерции.
Второе
основное произведение Галилея «Беседа о двух новых науках» было закончено после
катастрофы 1633 г. и вышло незадолго до смерти Галилея в 1638 г. в Нидерландах.
Исследуя
движение брошенных тел, Галилей писал, что когда тело движется по
горизонтальной плоскости, не встречая никакого сопротивления движению, то, как уже
ясно из всего изложенного выше, движение его является равномерным и
продолжалось бы бесконечно, если бы плоскость простиралась в пространстве без
конца. Если же плоскость конечна и расположена высоко, то тело, имеющее вес,
достигнув конца плоскости, продолжает двигаться далее таким образом, что к его
первоначальному равномерному беспрепятственному движению присоединяется другое,
вызываемое силой тяжести, благодаря чему возникает сложное движение,
слагающееся из равномерного горизонтального и естественного ускоренного
движения; он его называл движением бросаемых тел.
Галилей
доказывал, что траектория получающегося движения является полупараболой.
Прочитав приведенную выше формулировку, можно сделать вывод, что в ней
достаточно ясно выражено положение об инерционности по
крайней мере горизонтального равномерного движения. Однако такой вывод был бы
несколько преждевременным.
Участник
диалога «официальный оппонент» Сагредо указал, что ось полученной полупараболы
должна быть перпендикулярна к горизонту и оканчиваться в центре Земли. Так как
горизонтальное составляющее движение все время удаляет брошенное тело от оси
параболы, то никакое брошенное тело не может окончить движение в центре Земли;
следовательно, действительная траектория падающего тела не может быть указанной
полупараболой. В движении по упомянутой горизонтальной плоскости тело все время
удаляется от центра Земли, так что и это горизонтальное движение не может быть
равномерным.
Архимед в
своей механике и книге о квадратуре параболы принимает как правильный принцип,
что коромысло весов является прямой линией, равноудаленной во всех своих точках
от общего центра всех тяжелых тел, и что нити, к которым подвешены тяжелые
тела, параллельны между собой. Как Архимед, так и другие ученые, исходили в своих
рассуждениях из предположения бесконечной удаленности от нас земного центра.
При такой предпосылке заключения их совершенно справедливы и доказательства абсолютно строги.
Таким образом,
вся теория является лишь некоторым приближением к действительности, когда
небольшая дуга окружности может быть принята за отрезок прямой. Следовательно,
Галилею нельзя приписать честь открытия общего закона инерции: он знал его
только в той форме, которую ему придал Коперник, где траекториями инерционного
движения были окружности. Честь открытия закона инерции принадлежит Декарту.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов