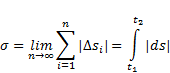Главная

Лекция 1. Кинематика точки и твердого тела.

В данной лекции рассматриваются следующие вопросы:

1. Краткие сведения по истории развития кинематики.

2. Кинематика точки. Введение в кинематику.

3. Способы задания движения точки.

4. Вектор скорости точки.

5. Вектор ускорения точки.

6. Определение скорости и ускорения точки при координатном способе задания движения точки.

7. Определение ускорения в полярных координатах.

8. Определение скорости и ускорения точки при естественном способе задания движения точки. Касательное и нормальное ускорение точки.

9. Некоторые частные случаи движения точки.

Изучение данных вопросов необходимо в дальнейшем для динамики движения материальной точки, динамики относительного движения точки, динамики вращательного движения точки, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».

Краткие сведения по истории развития кинематики

Кинематика, как специальный раздел теоретической механики, возникла позднее статики и динамики, а именно, в начале второй половины XIX в. Появление первых исследований по кинематике связано с изобретением огнестрельного оружия. В первую очередь внимание исследователей привлекали вопросы определения траектории полета снаряда, уточнение понятий о неравномерном и криволинейном движении точки. Леонардо да Винчи (1452—1519) первый экспериментально изучал вопрос о свободном вертикальном падении тяжелого тела. Однако лишь благодаря трудам Г. Галилея (1564—1642) развитие механики тесно связывается с запросами техники того времени. Галилею принадлежит введение понятия об ускорении и доказательство того, что траекторией движения снаряда, брошенного в пустоте под некоторым углом к горизонту, является парабола. Законы, найденные Галилеем, были развиты в исследованиях Э. Торричелли (1608—1647), установившем формулу пропорциональности скорости падения тела корню квадратному из высоты падения. Обобщение понятия ускорения на случай криволинейного движения было получено X. Гюйгенсом (1629—1695), который первым обратил внимание на возможность разложения ускорения при криволинейном движении на касательное и нормальное. Однако строгое доказательство этого было дано Л. Эйлером (1707—1783).

Кинематические законы движения планет были установлены И. Кеплером (1571—1630). Эти законы легли в основу закона всемирного тяготения, открытого Ньютоном.

Л. Эйлеру принадлежат основополагающие исследования по кинематике точки в случае естественного способа задания движения, по кинематике вращательного движения твердого тела вокруг неподвижной точки. Он создал широко применяемый метод кинематического описания движения твердого тела с помощью трех углов, называемых углами Эйлера.

Развитие кинематики системы обязано трудам Ж. Лагранжа (1736-1813).

Однако только бурный рост машиностроения в XIX в. повлек за собой расцвет кинематики как науки. По предложению Ж. Ампера в 1851 г. кинематика выделилась в особый раздел теоретической механики. Появляется ряд глубоких исследований по кинематике твердого тела французских ученых М. Шаля (1793—1886), Л. Пуансо, Г. Кориолиса (1792—1843). П. Л. Чебышев (1821—1894) создал в России научную школу по кинематике механизмов. Богатое научное наследие по кинематике механизмов Чебышева разрабатывается советскими учеными, среди которых, в первую очередь, следует отметить Н. И. Мерцалова (1860—1948), И. И. Артоболевского, А. П. Котельникова (1865—1940), Д. С. Зернова, Л. В. Асура (1878—1920), Я. Л. Геронимуса и др.

«Отцу русской авиации» Н. Е. Жуковскому (1847—1921) принадлежат первоклассные работы по теоретической механике, в том числе и по кинематике, в которых широко внедрены геометрические методы доказательств различных теорем. Ряд замечательных исследований по кинематике принадлежит профессору Одесского университета В. Н. Лигнину (1846—1900), возглавлявшему на Украине научное направление исследований по кинематике.

Кинематика точки. Введение в кинематику.

Кинематикой (от греческого «кинема» — движение) называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.

В кинематике изучают зависимости между пространственно-временными характеристиками механического движения. Поэтому кинематику называют также геометрией движения.

Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

Обычно кинематику подразделяют на две части — кинематику точки и кинематику твердого тела.

Механическое движение - это изменение положения тел (или частей тела) относительно друг друга в пространстве с течением времени.

Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета.

Тело отсчета - тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.

Система отсчета - это система координат, связанная с телом отсчета, и выбранный способ измерения времени (рис. 1).

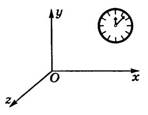
Рис.1

Изображать систему отсчета будем в виде трех координатных осей (не показывая тело, с которым они связаны).

Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство.

Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время t принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматриваются как изменяющиеся с течением времени, т.е. как функции времени t.

В теоретической механике при измерении пространства за основную единицу длины принимают метр (м), а за основную единицу времени — секунду (с). Время предполагается одинаковым в любых системах отсчета (системах координат) и не зависимым от движения этих систем относительно друг друга. Время обозначается буквой и рассматривается как непрерывно изменяющаяся величина, принимаемая в качестве аргумента.

При измерении времени в кинематике различают такие понятия, как промежуток времени, момент времени, начальный момент времени.

Промежутком времени называется время, протекающее между двумя физическими явлениями. Моментом времени называют границу между двумя смежными промежутками времени. Начальным моментом называется время, с которого начинают отсчет времени.

Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано).

Кинематически задать движение или закон движения тела (точки) - значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.

Основная задача кинематики точки и твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих данное движение.

Положение тела можно определить с помощью радиус-вектора или с помощью координат.

Радиус-вектор точки М - направленный отрезок прямой, соединяющий начало отсчета О с точкой М (рис. 2).

Координата х точки М - это проекция конца радиуса-вектора точки М на ось Ох. Обычно пользуются прямоугольной системой координат Декарта. В этом случае положение точки М на линии, плоскости и в пространстве определяют соответственно одним (х), двумя (х, у) и тремя (х, у, z) числами - координатами (рис. 2.1).

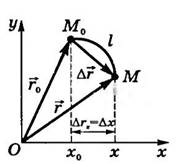
Рис.2

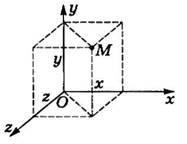
Рис.2.1

Материальная точка - тело, размерами которого в данных условиях можно пренебречь.

Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.

Основной задачей кинематики точки является изучение законов движения точки. Зависимость между произвольными положениями движущейся точки в пространстве и времени определяет закон ее движения. Закон движения точки считают известным, если можно определить положение точки в пространстве в произвольный момент времени. Положение точки рассматривается по отношению к выбранной системе координат.

Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.

В дальнейшем под словом "тело" будем понимать "материальная точка".

Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. На практике форму траектории задают с помощью математических формул (у=f(х) — уравнение траектории) или изображают на рисунке. Вид траектории зависит от выбора системы отсчета. Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей.

В зависимости от вида траектории различают прямолинейное и криволинейное движение.

Путь s - скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s> 0.

Перемещение тела за определенный промежуток времени - направленный отрезок прямой, соединяющий начальное (точка М₀) и конечное (точка М) положение тела (см. рис. 2):

,

где и — радиус-векторы тела в эти моменты времени.

Проекция перемещения на ось Ох: ∆r_x =∆х = х-х₀, где x₀ и x - координаты тела в начальный и конечный моменты времени.

Модуль перемещения не может быть больше пути: ≤s.

Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.

Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:

Способы задания движения точки

Для задания движения точки можно применять один из следующих трех способов:

1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки.

Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор , проведенный из начала координат О в точку М (рис. 3).

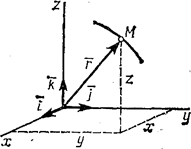
Рис.3

При движении точки М вектор будет с течением времени изменяться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргумента t:

Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.

Геометрическое место концов вектора , т.е. годограф этого вектора, определяет траекторию движущейся точки.

2. Координатный способ задания движения точки.

Положение точки можно непосредственно определять ее декартовыми координатами х, у, z (рис.3), которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т.е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости

x=f₁(t), y=f₂(t), z=f₃(t).

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

Чтобы получить уравнение траектории надо из уравнений движения исключить параметр t.

Нетрудно установить зависимость между векторным и координатным способами задания движения.

Разложим вектор на составляющие по осям координат:

где r_x, r_y, r_z - проекции вектора на оси; – единичные векторы направленные по осям, орты осей.

Так как начало вектора находится в начале координат, то проекции вектора будут равны координатам точки M. Поэтому

Если движение точки задано в полярных координатах

r=r(t), φ = φ(t),

где r — полярный радиус, φ — угол между полярной осью и полярным радиусом, то данные уравнения выражают уравнение траектории точки. Исключив параметр t, получим

r = r(φ).

Пример 1. Движение точки задано уравнениями

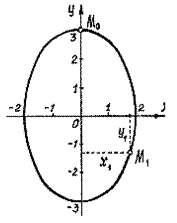
Рис.4

Чтобы исключить время, параметр t, найдём из первого уравнения sin2t=x/2, из второго cos2t=y/3. Затем возведём в квадрат и сложим. Так как sin²2t+cos²2t=1, получим . Это уравнение эллипса с полуосями 2 см и 3 см (рис.4).

Начальное положение точки M₀ (при t=0) определяется координатами x₀=0, y₀=3 см.

Через 1 сек. точка будет в положении M₁ с координатами

x₁=2sin2=2∙0,91=1,82 см, y₁=2cos2=3∙(-0,42)= -1,25 см.

Примечание.

Движение точки может быть задано с помощью и других координат. Например, цилиндрических или сферических. Среди них будут не только линейные размеры, но и углы. При необходимости, с заданием движения цилиндрическими и сферическими координатами можно познакомиться по учебникам.

3. Естественный способ задания движения точки.

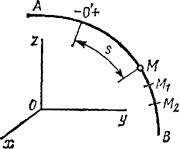
Рис.5

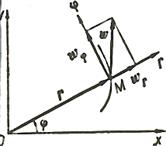
Естественным способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ является траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси).

Тогда положение точки М на траектории будет однозначно определяться криволинейной координатой s, которая равна расстоянию от точки О’ до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M₁, М₂,... . следовательно, расстояние s будет с течением времени изменяться.

Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость

s=f(t).

Уравнение выражает закон движения точки М вдоль траектории. Функция s= f(t) должна быть однозначной, непрерывной и дифференцируемой.

За положительное направление отсчета дуговой координаты s принимают направление движения точки в момент, когда она занимает положение О. Cледует помнить, что уравнение s=f(t) не определяет закон движения точки в пространстве, так как для определения положения точки в пространстве нужно знать еще траекторию точки с начальным положением точки на ней и фиксированное положительное направление. Таким образом, движение точки считается заданным естественным способом, если известна траектория и уравнение (или закон) движения точки по траектории.

Важно заметить, что дуговая координата точки s отлична от пройденного точкой по траектории пути σ. При своем движении точка проходит некоторый путь σ, которой является функцией времени t. Однако пройденный путь σ совпадает с расстоянием s лишь тогда, когда функция s = f(t) монотонно изменяется со временем, т.е. при движении точки в одном направлении. Допустим, что точка М переходит из М₁ в М₂. Положению точки в М₁ соответствует время t₁, а положению точки в М₂ - время t₂. Разложим промежуток времени t₂- t₁ на весьма малые промежутки времени ∆t₁ (i = 1,2, …n) так, чтобы в каждый из них точка совершала движение в одном направлении. Соответствующее приращение дуговой координаты обозначим ∆s_i. Пройденной точкой путь σ будет положительной величиной:

Если движение точки задано координатным способом, то пройденный путь определяется по формуле

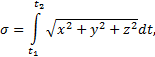
так как

где dx=xdt, dy= ydt, dz=zdt.

Следовательно,

Пример 2. Точка движется по прямой линии, по закону s=2t+3 (см) (рис. 6).

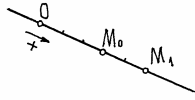
Рис.6

В начале движения, при t=0 s=OM₀=s₀=3 см. Положение точки M₀ называется начальным положением. При t=1 с, s=OM₁=5 см.

Конечно, за 1 сек. точка прошла расстояние M₀M₁=2 см. Так что s – это не путь пройденный точкой, а расстояние от начала отсчёта до точки.

Вектор скорости точки

Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.

Скорость - мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.

Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.

Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.

Для равномерно-прямолинейного движения

∆r=v∆t, (1)

где v – постоянный вектор.

Вектор v называется скоростью прямолинейного и равномерного движения полностью его определяет.

Из соотношения (1) видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени. Из (1) имеем

Направление вектора v указано на рис. 6.1.

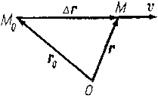
Рис.6.1

При неравномерном движении эта формула не годится. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени.

Пусть движущаяся точка находится в момент времени t в положении М, определяемом радиусом-вектором , а в момент t₁ приходит в положение M₁ определяемое вектором (рис.7). Тогда перемещение точки за промежуток времени ∆t=t₁-t определяется вектором который будем называть вектором перемещения точки. Из треугольника ОММ₁ видно, что ; следовательно,

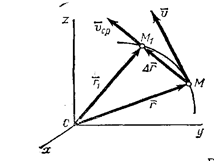
Рис. 7

Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени ∆t:

Скоростью точки в данный момент времени t называется векторная величина v, к которой стремится средняя скорость v_ср при стремлении промежутка времени ∆t к нулю:

Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени.

Так как предельным направлением секущей ММ₁ является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.

Определение скорости точки при координатном способе задания движения

Вектор скорости точки , учитывая, что r_x=x, r_y=y, r_z=z, найдем:

Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.

Зная проекции скорости, найдем ее модуль и направление (т.е. углы α, β, γ, которые вектор v образует с координатными осями) по формулам

Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени.

Направлен вектор скорости по касательной к траектории, которая нам наперед известна.

Определение скорости точки при естественном способе задания движения

Величину скорости можно определить как предел (∆r – длина хорды ММ₁):

где ∆s – длина дуги ММ₁. Первый предел равен единице, второй предел – производная ds/dt.

Следовательно, скорость точки есть первая производная по времени от закона движения:

Направлен вектор скорости, как было установлено ранее, по касательной к траектории. Если величина скорости в данный момент будет больше нуля, то вектор скорости направляется в положительном направлении

Вектор ускорения точки

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.

В СИ единицей ускорения является метр на секунду в квадрате .

Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость v, а в момент t₁ приходит в положение M₁ и имеет скорость v₁ (рис. 8).

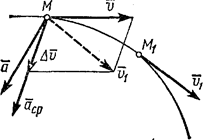
Рис.8

Тогда за промежуток времени ∆t=t₁-t скорость точки получает приращение . Для построения вектора отложим от точки М вектор, равный v₁, и построим параллелограмм, в котором диагональю будет , a одной из сторон . Тогда, очевидно, вторая сторона и будет изображать вектор . Заметим, что вектор всегда направлен в сторону вогнутости траектории.

Отношение приращения вектора скорости к соответствующему промежутку времени ∆t определяет вектор среднего ускорения точки за этот промежуток времени:

Вектор среднего ускорения имеет то же направление, что и вектор , т.е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени t называется векторная величина , к которой стремится среднее ускорение при стремлении промежутка времени ∆t к нулю: Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.

Ускорение точки равно нулю лишь тогда, когда скорость точки v постоянна как по величине, так и по направлению: это соответствует только прямолинейному и равномерному движению.

Найдем, как располагается вектор по отношению к траектории точки. При прямолинейном движении вектор направлен вдоль прямой, по которой движется точка.

При прямолинейном движении с возрастающей по модулю скоростью (рис. 9, а) векторы и сонаправлены () и проекция ускорения на направление движения положительна.

При прямолинейном движении с убывающей по модулю скоростью (рис. 9, б) направления векторов и противоположны () и проекция ускорения на направление движения отрицательна.

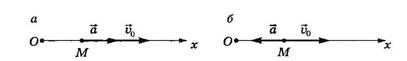
Рис.9

Если траекторией точки является плоская кривая, то вектор ускорения , так же как и вектор , лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор направлен в сторону вогнутости траектории и лежит в плоскости, проходящей через касательную к траектории в точке М и прямую, параллельную касательной в соседней точке M₁ (рис. 8). В пределе, когда точка М стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости, т.е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Следовательно, в общем случае вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.

Определение ускорения при координатном способе задания движения

Вектор ускорения точки в проекции на оси получаем:

Или

т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул

где α₁, β₁, γ₁ - углы, образуемые вектором ускорения с координатными осями.

Пример 3. Движение точки задано уравнениями x=2t, y=3-4t².

Из первого уравнения t=x/2. Подставив во второе, получим уравнение траектории: y=3-x²

Это уравнение параболы. В начале движения, при t=0, точка находилась на самом верху, в положении M₀ (x₀=0, y₀=3 см).

А, например, при t =0,5 c она будет в положении M с координатами x₁=1 см; y₁=2 см.

Проекции скорости на оси v_x==2см∙с^-1, v_y==-8t см∙с^-1.

При t =0,5 c, v_x=2см∙с^-1, v_y=-4 см∙с^-1.

И модуль скорости

Составляющие скорости по осям и вектор её показаны в масштабе на рис. 10.

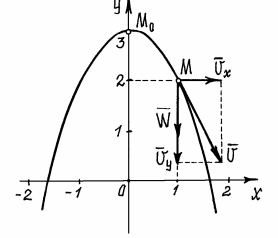
Рис.10

Проекции ускорения a_x= =0, a_y==-8 см∙с^-2. Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрицательна, то вектор ускорения направлен вертикально вниз, и величина его постоянна, не зависит от времени.

Определение ускорения в полярных координатах

Пусть движение точки М в плоскости Оху задано в полярных координатах r= r(t); φ= φ(t). Декартовы координаты выражаются через полярные по формулам

х= r∙соsφ, у= r∙sinφ.

Найдем проекции a_r и a_φ ускорение a точки на радиальное (r) и трансверсальное (φ) направление (рис.10.1)

Для a_x и a_y имеем выражение

a_x=a_rcosφ - a_φsinφ, a_y=a_rsinφ + a_φcosφ

C другой стороны,

a_x=x=rcosφ – 2rφsinφ – rcosφ ∙φ² – rsinφ ∙φ,

a_y=y=rsinφ + 2rφcosφ - rsinφ ∙φ² + rcosφ ∙φ.

Рис.10.1

Таким образом, получим

a_r=r – rφ², a_φ=2rφ + rφ.

Модуль ускорения

Обозначая через θ угол, образованный ускорением с положительным радиальным направлением, определим направление ускорения a точки по формуле

Определение ускорения при естественном способе задания движения. Касательное и нормальное ускорение точки

При естественном способе задания движения вектор определяют по его проекциям на оси Mτnb, имеющие начало в точке М и движущиеся вместе с нею (рис.11). Эти оси, называемые осями естественного трехгранника (или скоростными (естественными) осями), направлены следующим образом: ось Mτ - вдоль касательной к траектории в сторону положительного отсчета расстояния s; ось Mn - по нормали, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось Mb - перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль Mn, лежащая в соприкасающейся плоскости (в плоскости самой кривой, если кривая плоская), называется главной нормалью, а перпендикулярная к ней нормаль Mb - бинормалью.

Естественные оси – это подвижные оси, связанные с движущейся точкой М и образующие правую прямоугольную систему координат. Плоскость, проходящая через обе нормали (главную нормаль n и бинормаль b), называется нормальной плоскостью. Координатная плоскость, проходящая через касательную нормаль n, называется соприкасающейся плоскостью.

Соприкасающуюся плоскость в некоторой точке М кривой можно определить также, как предельное положение плоскости, проходящей через касательную в точке М и любую точку кривой М₁, когда последняя стремится в пределе к совпадению с точкой М.

При движении точки по траектории направления естественных осей непрерывно изменяются.

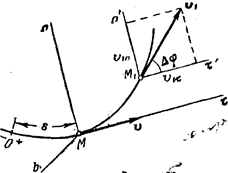
Рис.11

Было показано, что ускорение точки лежит в соприкасающейся плоскости, т.е. в плоскости Mτn; следовательно, проекция вектора на бинормаль равна нулю (a=0).

Вычислим проекции , на две другие оси. Пусть в момент времени t точка находится в положении М и имеет скорость v, a в момент t₁=t+∆t приходит в положение М₁ и имеет скорость v₁.

Тогда по определению

Перейдем в этом равенстве от векторов к их проекциям на оси Mτ и Mn, проведенные в точке М (рис.11). Тогда на основании теоремы о проекции суммы (или разности) векторов на ось получим:

Учитывая, что проекция вектора на параллельные оси одинаковы, проведем через точку М₁ оси , параллельные Mτ, Mn, и обозначим угол между направлением вектора и касательной Mτ через ∆φ. Этот угол между касательными к кривой в точках М и М₁ называется углом смежности.

Напомним, что предел отношения угла смежности ∆φ к длине дуги MM₁=∆s определяет кривизну k кривой в точке М. Кривизна же является величиной, обратной радиусу кривизны ρ в точке М. Таким образом,

Обращаясь теперь к чертежу (рис.11), находим, что проекции векторов и на оси Mτ, Mn, будут равны:

где v и v₁ - численные величины скорости точки в моменты t и t₁.

Следовательно,

Заметим что при ∆t→0 точка М₁ неограниченно приближается к М и одновременно

Тогда, учитывая, что в пределе , получим для a_τ выражение

Правую часть выражения a_n преобразуем так, чтобы в нее вошли отношения, пределы которых нам известны. Для этого умножим числитель и знаменатель дроби, стоящей под знаком предела, на ∆φ∆s. Тогда будем иметь

так как пределы каждого из стоящих в скобке сомножителей при ∆t→0 равны:

Окончательно получаем:

Итак, мы доказали, что проекция ускорения точки на касательную равна первой производной от численной величины скорости или второй производной от расстояния (криволинейной координаты) s no времени, а проекция ускорения на главную нормаль равна квадрату скорости деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю (a_b=0). Эти результаты выражают собою одну из важных теорем кинематики точки.

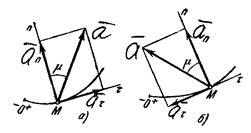
Рис.12

Отложим вдоль касательной Mτ и главной нормали Mn векторы и , численно равные a_τ и a_n (рис. 12). Эти векторы изображают касательную и нормальную составляющие ускорения точки. При этом составляющая будет всегда направлена в сторону вогнутости кривой (величина a всегда положительна), а составляющая может быть направлена или в положительном, или в отрицательном направлении оси Mτ в зависимости от знака проекции a_τ (см. рис.12, а и б).

Вектор ускорения точки изображается диагональю параллелограмма, построенного на составляющих и . Так как эти составляющие взаимно перпендикулярны, то по модулю:

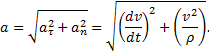
Относительность движения. Сложение скоростей

Как отмечалось выше, для описания движения тела необходимо выбрать тело отсчета и связать с ним систему координат. В качестве тела отсчета может выступать любое тело.

В разных системах отсчета будут различны вид траектории, значения скорости, перемещения и других величин. В этом и заключается относительность движения.

Например, человек идет по палубе парохода со скоростью относительно парохода. Пароход движется поступательно со скоростью относительно берега. Найдем скорость человека относительно берега.

Свяжем неподвижную систему отсчета (хОу) с Землей, а подвижную (х'О'у') — с пароходом.

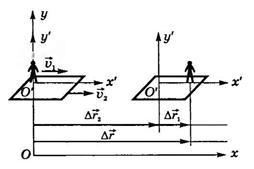
Рис.13

Из рис.13 видно, что перемещение

(1)

где — перемещение человека относительно парохода, — перемещение парохода относительно берега, — перемещение человека относительно берега.

Таким образом, если тело одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею в каждом из движений. В этом состоит установленный экспериментально принцип независимости движений.

Разделив уравнение (1) на промежуток времени, за который произошли перемещения человека и парохода, получим закон сложения скоростей:

Скорость тела относительно неподвижной системы отсчета равна геометрической сумме скорости тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной.

Закон сложения скоростей справедлив и для неравномерного движения, только в этом случае - мгновенные скорости.

Этот закон был установлен Г. Галилеем. Он справедлив только для движений со скоростями, намного меньшими скорости света с = 3∙10⁸ (м/с). Такие скорости в физике называют нерелятивистскими.

Некоторые частные случаи движения точки.

Пользуясь полученными результатами, рассмотрим некоторые частные случаи движения точки.

Равномерное прямолинейное движение

Равномерное прямолинейное движение - это движение, при котором тело за любые равные промежутки времени совершает равные перемещения, т. е. это движение с постоянной по модулю и направлению скоростью:

— уравнение скорости,

— уравнение ускорения.

Пусть в момент времени t₀=0 координата тела х₀, в момент t - х (рис. 14).

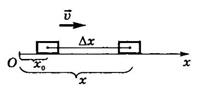
Рис.14

Тогда за промежуток времени Δt=t-t₀=t координата X тела изменилась на величину ∆х = х - х₀. Следовательно, проекция скорости тела

,следовательно,

x=x₀+v_xt- кинематическое уравнение равномерного движения (уравнение зависимости координаты от времени).

Проекция перемещения ∆r_x=х-х₀

∆r_x=v_xt - уравнение перемещения.

При равномерном прямолинейном движении направление скорости не изменяется, поэтому путь . Следовательно, — уравнение пути.

Зависимость кинематических величин от времени можно изобразить графически.

Изобразим графики скорости, перемещения, пути и координаты для трех тел: 1, 2, 3 (рис. 15).

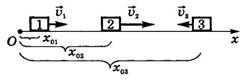
Рис.15

Тела 1, 2 движутся в положительном направлении оси Ох, причем ; тело 3 движется в направлении, противоположном оси Ох; их начальные координаты соответственно , . Графики скорости представлены на рис.16. Площадь заштрихованного прямоугольника численно равна пути s (модулю перемещения), пройденному телом 1 за время t₁. На рис.17 даны графики перемещения , на рис.18 - графики пути s=f(t).

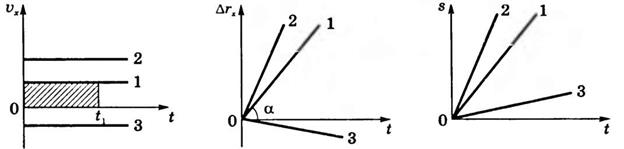
Рис.16 Рис.17 Рис.18

Наклон графика , к оси времени зависит от модуля скорости: .

Графики движения (зависимости координаты от времени) изображены на рис.19.

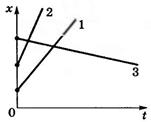
Рис.19

С помощью графика движения можно определить:

1) координаты тела в любой момент времени;

2) путь, пройденный телом за некоторый промежуток времени;

3) время, за которое пройден какой-то путь;

4) кратчайшее расстояние между телами в любой момент времени;

5) момент и место встречи тел и др.

Равноускоренное прямолинейное движение

Равноускоренное прямолинейное движение - это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением.

=сonst — уравнение ускорения.

По определению ускорения .

Пусть в момент времени t₀ скорость тела равна , в момент времени t - . Тогда за промежуток времени ∆t=t-t₀=t скорость изменилась на . Следовательно, ускорение

— уравнение скорости.

Или в проекциях: .

Эти зависимости кинематических величин от времени изобразим графически для трех тел (рис.20).

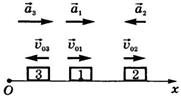
Рис.20

Графики ускорения представлены на рис.21, а графики скорости - на рис.22.

Для нахождения перемещения воспользуемся графиком скорости (рис.23). Для малого промежутка времени ∆t изменением величины скорости можно пренебречь и скорость можно считать постоянной. Тогда перемещение за промежуток времени ∆t будет равно площади узкой густо заштрихованной полоски. Мысленно разбив все время движения тела на малые промежутки времени и найдя перемещение за каждый отдельный промежуток времени, суммируем эти перемещения. Модуль проекции перемещения за промежуток времени ∆t=t-t₀=t в пределе численно равен площади заштрихованной трапеции.

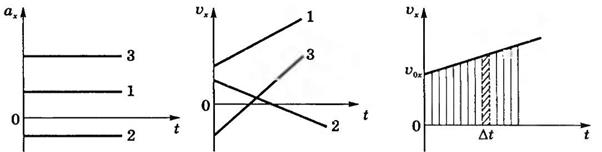
Рис.21 Рис.22 Рис.23

Следовательно, (2)

Подставив значение в (2), получим:

— уравнение перемещения в проекциях;

— уравнение перемещения в векторном виде.

Учитывая, что х=х₀+∆r_х, имеем:

— кинематическое уравнение равноускоренного движения.

Его векторный вид:

Исключая из уравнений скорости и перемещения время t, получим:

.

Сравнивая выражение (2) с формулой , найдем:

- проекция средней скорости при равноускоренном движении.

Графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения (рис.24).

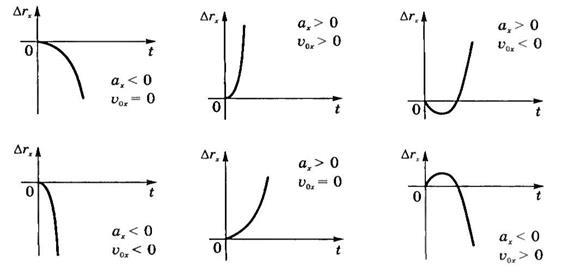
Рис.24

Равномерное криволинейное движение

Равномерным называется такое криволинейное движение точки, в котором численная величина скорости все время остается постоянной: v=const.

Тогда и все ускорение точки равно одному только нормальному:

Вектор ускорения направлен при этом все время по нормали к траектории точки.

Так как в данном случае ускорение появляется только за счет изменения направления скорости, то отсюда заключаем, что нормальное ускорение характеризует изменение скорости по направлению. Найдем закон равномерного криволинейного движения.

Из формулы имеем ds=vdt.

Пусть в начальный момент (t=0) точка находится от начала отсчета на расстоянии s₀. Тогда, беря от левой и правой части равенства определенные интегралы в соответствующих пределах, получим

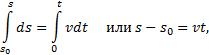
так как v=const. Окончательно находим закон равномерного криволинейного движения в виде

s=s₀+vt.

Если s₀=0, то s даст путь, пройденный точкой за время t. Следовательно, при равномерном движении путь, пройденный точкой, расчет пропорционального времени, а скорость движения равна отношению пути ко времени

s=vt, v=s/t.

Равнопеременное криволинейное движение.

Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиною постоянной: a_τ=const. Найдем закон этого движения, считая, что при t=0: s=s₀, а v=v₀, где v₀ - начальная скорость точки. Согласно формуле имеем dv=a_τdt.

Так как a_τ=const, то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:

v=v₀+a_τt.

Формулу представим в виде

Вторично интегрируя, найдем закон равнопеременного криволинейного движения точки в виде

Если при криволинейном движении точки модуль скорости возрастает, то движение называется ускоренным, а если убывает - замедленным.

Свободное падение тел. Ускорение свободного падения

Свободное падение - это движение тела под действием только силы тяжести.

На тело, падающее в воздухе, кроме силы тяжести действует сила сопротивления воздуха, следовательно, такое движение не является свободным падением. Свободное падение — это падение тел в вакууме.

Ускорение , которое сообщает телу сила тяжести, называют ускорением свободного падения. Оно показывает, на какую величину изменяется скорость свободно падающего тела за единицу времени.

Ускорение свободного падения направлено вертикально вниз.

Галилео Галилей установил (закон Галилея): все тела падают на поверхность Земли под действием земного притяжения при отсутствии сил сопротивления с одинаковым ускорением, т.е. ускорение свободного падения не зависит от массы тела.

Убедиться в этом можно, используя трубку Ньютона или стробоскопический метод.

Трубка Ньютона представляет собой стеклянную трубку длиной около 1 м, один конец которой запаян, а другой снабжен краном (рис. 25).

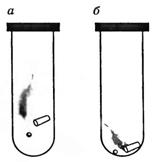
Рис.25

Поместим в трубку три разных предмета, например дробинку, пробку и птичье перо. Затем быстро перевернем трубку. Все три тела упадут на дно трубки, но в разное время: сначала дробинка, затем пробка и, наконец, перо. Но так падают тела в том случае, когда в трубке есть воздух (рис. 25, а). Стоит только воздух откачать насосом и снова перевернуть трубку, мы увидим, что все три тела упадут одновременно (рис. 25, б).

В земных условиях g зависит от географической широты местности.

Наибольшее значение оно имеет на полюсе g=9,81 м/с², наименьшее — на экваторе g=9,75 м/с². Причины этого:

1) суточное вращение Земли вокруг своей оси;

2) отклонение формы Земли от сферической;

3) неоднородное распределение плотности земных пород.

Ускорение свободного падения зависит от высоты h тела над поверхностью планеты. Его, если пренебречь вращением планеты, можно рассчитать по формуле:

где G — гравитационная постоянная, М — масса планеты, R — радиус планеты.

Как следует из последней формулы, с увеличением высоты подъема тела над поверхностью планеты ускорение свободного падения уменьшается. Если пренебречь вращением планеты, то на поверхности планеты радиусом R

Для небольших высот (g<<h) можно считать g=const, для таких высот свободное падение является равноускоренным движением.

Для его описания можно использовать формулы равноускоренного движения:

уравнение скорости:

кинематическое уравнение, описывающее свободное падение тел: ,

или в проекции на ось .

Движение тела, брошенного вертикально

Свободно падающее тело может двигаться прямолинейно или по криволинейной траектории. Это зависит от начальных условий. Рассмотрим это подробнее.

Свободное падение без начальной скорости (=0) (рис. 26).

При выбранной системе координат движение тела описывается уравнениями: .

Из последней формулы можно найти время падения тела с высоты h:

.

Подставляя найденное время в формулу для скорости, получим модуль скорости тела в момент падения: .

Движение тела, брошенного вертикально вверх с начальной скоростью (рис. 27)

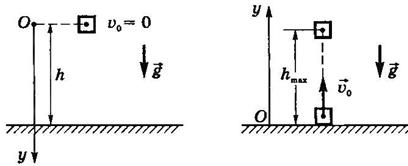
Рис.26 Рис.27

Движение тела описывается уравнениями:

Из уравнения скорости видно, что тело движется равнозамедленно вверх, достигает максимальной высоты, а затем движется равноускоренно вниз. Учитывая, что при y=hmax скорость и в момент достижения телом первоначального положения у=0, можно найти:

— время подъема тела на максимальную высоту;

— максимальная высота подъема тела;

— время полета тела;

— проекция скорости в момент достижения телом первоначального положения.

Движение тела, брошенного горизонтально

Если скорость направлена не вертикально, то движение тела будет криволинейным.

Рассмотрим движение тела, брошенного горизонтально с высоты h со скоростью (рис. 28). Сопротивлением воздуха будем пренебрегать. Для описания движения необходимо выбрать две оси координат — Ох и Оу. Начало отсчета координат совместим с начальным положением тела. Из рис.28 видно, что , , , .

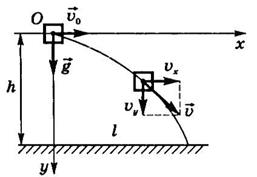
Рис.28

Тогда движение тела опишется уравнениями:

, (3)

, (4)

Анализ этих формул показывает, что в горизонтальном направлении скорость тела остается неизменной, т.е. тело движется равномерно. В вертикальном направлении тело движется равноускоренно с ускорением g, т.е. так же, как тело, свободно падающее без начальной скорости. Найдем уравнение траектории. Для этого из уравнения (3) найдем время

и, подставив его значение в формулу (4), получим:

Это уравнение параболы. Следовательно, тело, брошенное горизонтально, движется по параболе. Скорость тела в любой момент времени направлена по касательной к параболе (см. рис. 28). Модуль скорости можно рассчитать по теореме Пифагора:

Зная высоту h, с которой брошено тело, можно найти время t1, через которое тело упадет на землю. В этот момент координата у равна высоте у₁=h. Из уравнения (4) находим:

Отсюда

Формула (5) определяет время полета тела. За это время тело пройдет в горизонтальном направлении расстояние l, которое называют дальностью полета и которое можно найти на основании формулы (3), учитывая, что l=x₁. Следовательно, — дальность полета тела. Модуль скорости тела в этот момент .

Движение тела, брошенного под углом к горизонту

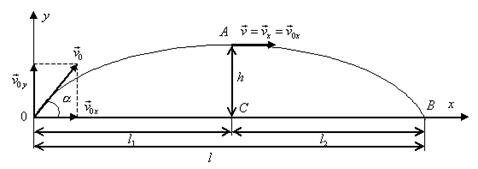
Пусть тело брошено под углом α к горизонту со скоростью . Как и в предыдущих случаях, будем пренебрегать сопротивлением воздуха. Для описания движения необходимо выбрать две оси координат — Ох и Оу (рис. 29).

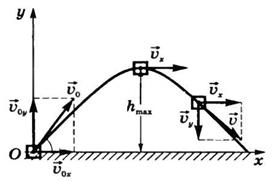
Рис.29

Начало отсчета совместим с начальным положением тела. Проекции начальной скорости на оси Оу и Ох: , . Проекции ускорения: ,

Тогда движение тела будет описываться уравнениями:

(6)

(7)

(8)

(9)

Из этих формул следует, что в горизонтальном направлении тело движется равномерно, а в вертикальном — равноускоренно.

Траекторией движения тела будет парабола. Учитывая, что в верхней точке параболы , можно найти время подъема тела до верхней точки параболы:

Подставив значение t₁ в уравнение (8), найдем максимальную высоту подъема тела:

— максимальная высота подъема тела.

Время полета тела находим из условия, что при t=t₂ координата у₂=0. Следовательно, . Отсюда, — время полета тела. Сравнивая эту формулу с формулой (10), видим, что t₂=2t₁.

Время движения тела с максимальной высоты t₃=t₂-t₁=2t₁-t₁=t₁. Следовательно, сколько времени тело поднимается на максимальную высоту, столько времени оно опускается с этой высоты. Подставляя в уравнение координаты х (6) значение времени t₂, найдем:

- дальность полета тела.

Мгновенная скорость в любой точке траектории направлена по касательной к траектории (см. рис. 29), модуль скорости определяется по формуле

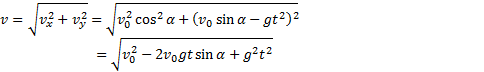
Таким образом, движение тела, брошенного под углом к горизонту или в горизонтальном направлении, можно рассматривать как результат двух независимых движений — горизонтального равномерного и вертикального равноускоренного (свободного падения без начальной скорости или движения тела, брошенного вертикально вверх).

Методические рекомендации по решению задач

Рассмотрим, что может быть целью кинематических задач.

1. Нас может интересовать изменение кинематических величин в процессе движения, т.е. получение сведений об изменении координат, скорости, ускорения, а также соответствующих угловых величин.

2. В ряде задач, например, в задаче о движении тела под углом к горизонту, требуется узнать о значениях физических величин в конкретных состояниях: дальности полета, наибольшей величине подъема и т.д.

3. В случаях, когда тело одновременно участвует в нескольких движениях (например, качение шара) или рассматривается относительное движение нескольких тел, возникает необходимость установить соотношения между перемещениями, скоростями и ускорениями (линейными и угловыми), т.е. найти уравнения кинематической связи.

Несмотря на большое разнообразие задач по кинематике, можно предложить следующий алгоритм их решения:

1. Сделать схематический рисунок, изобразив начальное положение тел и их начальное состояние, т.е. и .

2. Выбрать систему отсчета на основании анализа условия задачи. Для этого нужно выбрать тело отсчета и связать с ним систему координат, указав начало отсчета координат, направление осей координат, момент начала отсчета времени. При выборе положительных направлений руководствуются направлением движения (скорости) или направлением ускорения.

3. Составить на основании законов движения систему уравнений в векторном виде для всех тел, а затем в скалярной форме, спроецировав на координатные оси эти векторные уравнения движения. При записи этих уравнений следует обратить внимание на знаки "+" и "-" проекций входящих в них векторных величин.

4. Ответ необходимо получить в виде аналитической формулы (в общем виде), а в конце произвести числовые расчеты.

Пример 4. Даны уравнения движения точки х = 3t; y=9t^2--4; где х, у - в см, t - в с. Найти уравнение траектории точки и для момента времени t₁ = 1с найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Решение. Уравнения движения точки можно рассматривать как параметрические уравнения ее траектории. Чтобы получить уравнения траектории точки в координатной форме, исключим время t из уравнений ее движения

Траекторией точки является парабола.

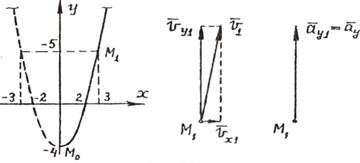
При t₀ = 0 и t₁ = 1 с соответственно получаем точки М₀(0,- 4) и М₁(3,5).

Скорость и ускорение точки

v_х== 3 [см/с];

v_у = = 18t [см/с];

а_х= = 0;

а_у = = 18 [см/с²].

Заметим, что v_x, а_х и а_у не зависят от времени t.

При t_l = 1 с получаем

Касательное и нормальное ускорения точки при t₁ = 1 с

На рисунке показано положение точки М в заданный момент времени(t₁ = 1 с), а также выполнено построение векторов скорости и ускорения точки. Вектор ₁ построен по составляющим и ; этот вектор совпадает по направлению с направлением касательной к траектории. Вектор , построен по составляющим и .

Радиус кривизны траектории при t₁ = 1 с

Расчеты показывают, что радиус кривизны траектории в точке М₀(0,4) при t₀ = 0, ρ₀ = 0,5 [см].

Пример 5. Локомотив движется со скоростью 54 км/ч. При торможении он приобретает ускорение 0,5 м/с². Найти, на каком расстоянии от пункта остановки надо начать торможение и сколько времени оно будет продолжаться.

Решение. Локомотив, принятый за точку, совершает равнозамедленное движение в соответствии с уравнениями

Используя условия задачи, получим

где v₀ = 54 [км/ч] = 15 [м/с]; а = 0,5 [м/с²]; s₀ = 0.

Из составленной системы уравнений находим время остановки и путь остановки локомотива

Пример 6. Сколько времени пассажир, сидящий у окна поезда, который идет со скоростью 54 км/ч, будет видеть проходящий мимо него встречный поезд, скорость которого 36 км/ч, а длина 250 м?

Дано:

Найти: t.

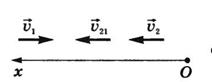
Решение. Неподвижную систему отсчета свяжем с Землей, подвижную – с поездом, в котором находится пассажир. Согласно закону сложения скоростей , где - скорость встречного поезда относительно первого. В проекциях на ось Ох:

.

Так как путь, пройденный встречным поездом относительно первого, равен длине поезда, то время

, t=10 c.

Пример 7. Пароход идет от Нижнего Новгорода до Астрахани 5,0 суток, а обратно - 7,0 суток. Как долго будет плыть плот от Нижнего Новгорода до Астрахани? Стоянки и задержки в движении исключить.

Дано: t₁=5 сут, t₂=7 сут.

Найти: t₃

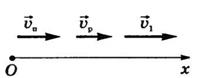
Решение. Неподвижную систему отсчета свяжем с берегом, подвижную – с водой. Будем считать, что скорость воды на всем пути одинакова и скорость парохода относительно воды постоянна и равна модулю мгновенной скорости парохода относительно воды.

Так как плот движется относительно берега со скоростью течения реки , то время его движения , где s – расстояние между городами. При движении парохода по течению его скорость согласно закону сложения скоростей , или в проекциях на ось Ох:

(1)

где - скорость парохода относительно берега, - скорость парохода относительно реки.

Зная время движения, можно найти скорость:

(2)

Из формул (1) и (2) имеем:

(3)

При движении парохода против течения , или в проекциях на ось Ох , где - скорость парохода относительно берега.

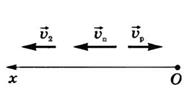
С другой стороны, . Тогда

(4)

Решая систему уравнений (3) и (4) относительно , получим:

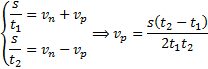
Найдем время движения плота:

t₃=35 сут.

Пример 8. При равноускоренном движении тело проходит за два первых равных последовательных промежутка времени по 4,0 с каждый пути s₁ = 24 м и s₂=64 м соответственно. Определите начальную скорость и ускорение тела.

Дано: t₁=t₂= 4,0 с, s₁ =24 м, s₂ = 64 м.

Найти: .

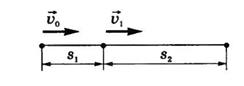
Решение. Запишем уравнения пути для s₁ и (s₁+s₂) соответственно. Так как начальная скорость в этом случае одинакова, то

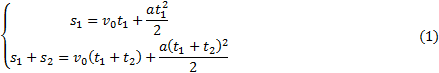
Так как t1=t2, то

(2)

Выразив из (1) и подставив ее в (2), получим:

Тогда начальная скорость

Пример 9. Автомобиль, двигаясь по прямолинейной траектории равноускоренно с начальной скоростью 5,0 м/с, прошел за первую секунду путь, равный 6,0 м. Найдите ускорение автомобиля, мгновенную скорость в конце второй секунды и перемещение за 2,0 с.

Дано:

Найти:

Решение. Зная путь, пройденный телом за первую секунду, можно найти ускорение:

Скорость в конце второй секунды найдем по формуле

Перемещение за 2 с можно рассчитать по формулам:

Пример 10. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x = A + Bt + Ct³, где А=4 м, В=2м/с, С=-0,5 м/с³.

Для момента времени t₁=2 c определить: 1) координату точки х₁ точки; 2) мгновенную скорость v₁; 3) мгновенное ускорение а₁.

Дано: x = A + Bt + Ct³, А=4 м, В=2 м/с, С=-0,5 м/с³, t₁=2 c.

Найти: х₁; v₁; а₁.

Решение. 1.Подставим в уравнение движения вместо t заданное значение времени t₁: x₁ = A + Bt₁ + Ct₁³. Подставим в это выражение значения А, В, С, t₁ и произведем вычисления: х₁ = 4 м.

2. Мгновенная скорость: Тогда в момент времени t₁ мгновенная скорость v₁ = B + 3Ct₁². Подставим сюда значения В,С, t₁: v₁= – 4 м/с. Знак минус указывает на то, что в момент времени t₁=2 c точка движется в отрицательном направлении координатной оси.

3. Мгновенное ускорение: Мгновенное ускорение в момент времени t₁ равно а₁ = 6Сt₁. Подставим значения С, t₁: а₁= –6 м/с². Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.

Пример 11. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид х = A + Bt + Ct², где А=5 м, В=4м/с, С= -1м/с². Определить среднюю скорость v_хср за интервал времени от t₁=1 c до t₂=6 c.

Дано: х = A + Bt + Ct² , А=5м, В=4м/с, С=- 1м/с², t₁=1 c , t₂=6 c.

Найти: v_хср -? а_хср -?

Решение. Средняя скорость за интервал времени t₂-t₁ определяется выражением v_ср=(х₂-х₁)/(t₂- t₁).

х₁ = A + Bt₁ + Ct₁²= 8 м, х₂ = A + Bt₂ + Ct₂²= –7 м.

Подставим значения х₁, х₂, t₁ , t₂ и произведем вычисления: v_хср= -3 м/с.

Пример 12. Из вертолета, находящегося на высоте h = 300 м, сбросили груз. Через какое время груз достигнет земли, если: а) вертолет неподвижен; б) вертолет опускается со скоростью v₀=5 м/с; 3) вертолет поднимается со скоростью v₀=5 м/с. Описать графически соответствующие движения груза в осях s(t), v(t) и a(t).

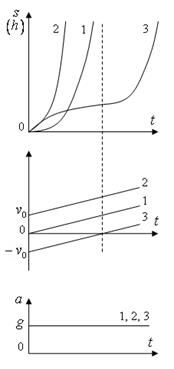
Решение. а) Груз, покинувший неподвижный вертолет, свободно падает, т.е. движется равноускоренно с ускорением свободного падения g. Время движения найдем из соотношения Откуда Графики движение объекта отмечены 1 на рисунке.

б) Движение груза, покинувшего вертолет, который опускается с постоянной скоростью v₀=5 м/с, является равноускоренным движением с постоянным ускорением g и описывается уравнением

Подстановка численных значений дает уравнение 9,8t²+10t-600=0.

Отрицательный результат не имеет физического смысла, поэтому время движения t=7,57 с.

Графики движение объекта отмечены 2 на рисунке.

3) Движение груза, покинувшего вертолет, который поднимается с постоянной скоростью v₀=5 м/с, cостоит из двух этапов. На первом этапе – груз движется равнозамедленно с постоянным ускорением g, направленным противоположно скорости, и описывается уравнениями

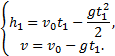
В верхней точке траектории скорость становится равной нулю, поэтому

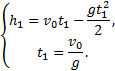
Подставляя второе уравнение системы в первое, получим

На втором этапе – свободное падение с высоты h₀=h+h₁=300+1,28=301,28 м.

Поскольку

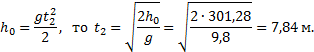
Графики движение объекта отмечены 3 на рисунке.

Пример 13. С воздушного шара, опускающегося вниз с постоянной скоростью 2 м/с, бросили вертикально вверх груз со скоростью 18 м/c относительно земли. Определить расстояние между шаром и грузом в момент, когда груз достигает высшей точки своего подъема. Через какое время груз пролетит мимо шара, падая вниз.

Дано: v₀₁= 2 м/с, v₀₂=18 м/c

Найти: s-? τ -?

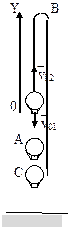
Решение. Направим ось 0Y вертикально вверх, начало совместим с точкой 0, в которой находился шар в момент бросания груза.

Тогда уравнения движения груза и воздушного шара:

Скорость движения груза изменяется по закону v₂=v₀₂ – gt.

В наивысшей точке В подъема груза v₂=0. Тогда время подъема до этой точки Координата груза в точке В

За это время воздушный шар опустился до точки А; его координата

Расстояние между точками А и В:

Через промежуток времени τ, когда камень пролетит мимо шара, координаты тел будут одинаковы: у_1С=у_2С;

Отсюда

Пример 14. С какой скоростью и по какому курсу должен лететь самолет, чтобы за два часа пролететь на север 300 км, если во время полета дует северо-западный ветер под углом 30^о к меридиану со скоростью 27 км/ч?

Дано: t=7,2∙10³ c; l=3∙10⁵ м; α=30° ≈ 0,52 рад; v₂ ≈7,2 м/с.

Найти: v₂ -? φ -?

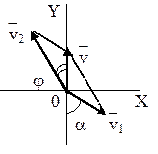
Решение. Рассмотрим движение самолета в системе отсчета, связанной с землей.

Проведем ось ОХ в направлении на восток, а ось OY - на север. Тогда скорость движения самолета в выбранной системе отсчета

(1)

где v=l/t (2)

Уравнение (1) в проекции на оси

ОХ: 0=v₁∙sinα – v₂∙sinφ;

OY: v= v₂∙cosφ - v₁∙cosα, или v₁∙sinα = v₂∙sinφ, v₂∙cosφ=v₁∙cosα + v (3)

Разделив эти уравнения почленно, получим tgφ=v₁sinα/(v₁cosα+ v),

или с учетом (2)

tgφ=v₁∙sinα/(v₁∙cosα+ l/t);

φ=arctgv₁∙sinα/(v₁∙cosα+ l/t) ≈0,078 рад.

Возводя в квадрат правые и левые части уравнений (3) и складывая полученные уравнения, находим

v₂²∙sin²φ + v₂² ∙cos²φ = v₁² sin²α+ (v₁∙cosα + v)²,

откуда , или с учетом (2)

Пример 15. Тело, брошенное вертикально вверх, вернулось на землю через t=3 с. Найти высоту подъема тела и его начальную скорость.

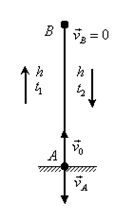
Решение. Движение тела вверх является равнозамедленным с ускорением - g и происходит в течение времени t₁, а движение вниз – равноускоренным с ускорением g и происходит в течение времени t₂. Уравнения, описывающие движение на участках АВ и ВА, образуют систему:

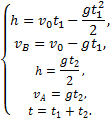
Поскольку v_B=0, то v₀=gt₁. Подставив v₀ в первое уравнение системы, получим . Если сравнить это выражение с третьим уравнением системы, то можно сделать вывод о том, что время подъема равно времени спуска t₁=t₂=t/2=1,5с. Начальная скорость и скорость при приземлении равны друг другу и составляют v₀=v_A=gt₁=9,8∙1,5=14,7 м/с.

Высота подъема тела

Пример 16. Свободно падающее тело в последнюю секунду движения прошло половину пути. Найти высоту, с которой оно брошено и время движения.

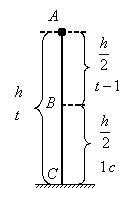
Решение. Зависимость пройденного пути от времени для свободно падающего тела . Поскольку участок ВС, составляющие половину всего пути, пройден за время, равное 1 с, то первая половина пути АВ пройдена за время (t-1) с. Тогда движение на участке ВС может быть описано как .

Решая систему

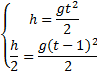
получим t²-4t+2=0. Корни этого уравнения t₁=3,41 с и t₂=0,59 с. Второй корень не подходит, т.к. время движения, исходя из условия задачи, должно превышать одну секунду. Следовательно, тело падало в течение 3,41 с и прошло за это время путь

Пример 17. С башни высотой 25 м горизонтально брошен камень со скоростью 15 м/с.

Найти: 1) сколько времени камень будет в движении, 2) на каком расстоянии он упадет на землю, 3) с какой скоростью он упадет на землю, 4) какой угол составит траектория камня с горизонтом в точке его падения на землю. Сопротивление воздуха не учитывать.

Дано: Н=25 м, v_o=15 м/с

Найти: t-? s_x- ? v - ? φ- ?

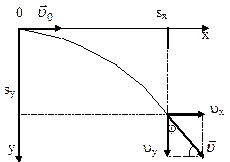
Решение. Перемещение брошенного горизонтально камня можно разложить на два: горизонтальное s_x и вертикальное s_y:

s_y=H=gt²/2,

s_x=v_ot,

где t - время движения.

Отсюда:

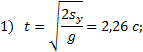
2) s_x=v_ot= 33,9 м;

3) v_y=gt=22,1м/с;

4) sinφ= v_y/v=0,827;

φ=55^о48’.

Пример 18. С башни высотой 25 м горизонтально со скоростью v_x=10 м/c брошено тело.

Найти: 1) время t падения тела, 2) на каком расстоянии l от основания башни оно упадет, 3) скорость v в конце падения, 4) угол, который составит траектория тела с землей в точке его приземления.

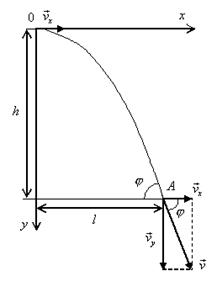
Решение. Движение тела является сложным. Оно участвует в равномерном движении по горизонтали и равноускоренном с ускорением g по вертикали. Поэтому участок АВ описывается уравнениями:

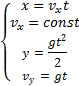
Для точки А эти уравнения принимают вид:

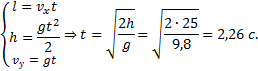
Тогда l=10∙2,26=22,6 м, а v_y=9,8∙2,26=22,15 м/с.

Поскольку , то

Угол, который траектория составляет с землей, равен углу φ в треугольнике скоростей в т. А, тангенс которого , поэтому φ=68,7°.

Пример 19. Для тела, брошенного с горизонтальной скоростью v_x=10 м/с, через время t=2 с после начала движения найти: нормальное, тангенциальное и полное ускорения, а также радиус кривизны траектории в этой точке.

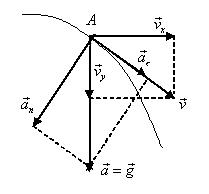
Решение. Вертикальная составляющая скорости v_y=gt=9,8∙2=19,6 м/с

Скорость в точке А:

, то

Векторы образуют треугольник скоростей, а векторы - треугольник ускорений. Как видно из рисунка, эти треугольники подобны, а это означает, что их стороны пропорциональны: .

Отсюда,

Нормальное ускорение , поэтому радиус кривизны траектории

Пример 20. Мяч бросили со скоростью 10 м/с под углом 40^о к горизонту.

Найти: 1) на какую высоту поднимется мяч; 2) на каком расстоянии от места бросания мяч упадет на землю, 3) сколько времени он будет в движении.

Дано: v_o=10 м/с, α=40^о.

Найти: s_y - ? s_x - ? t - ?

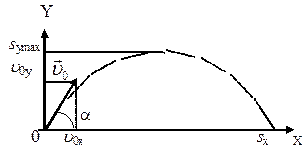
Решение. 1) Найдем наибольшую высоту s_{y max}, на которую поднимается тело, брошенное со скоростью v_o под углом α к горизонту. Имеем (см. рис.):

v_y=v_o sinα – gt; (1)

s_y=v_ot∙sinα – gt²/2. (2)

В верхней точке v_y=0 и из (1) получим v_o∙sin𝛼 = gt₁, отсюда время подъема мяча t₁=v_o∙sinα/g. Подставляя t₁ в (2), получим

s_{y max}= v_o² ∙sin²α/(2g)= 2,1 м.

2) Найдем дальность полета s_{x max} тела, брошенного под углом к горизонту.

Имеем: v_x=v_o∙cosα, (3)

s_x=v_xt=v_ot∙cosα. (4)

Тело упадет на горизонтальную плоскость через время t₂=2t₁=2v_osinα/g.

Подставляя t₂ в (4), получим s_xmax = v_о² sin2α/g=10,0 м.

3) t₂=2t₁=2v_osinα/g=1,3 с.

Пример 21. Тело брошено со скоростью v₀=10 м/с² под углом α=30° к горизонту. На какую высоту тело поднимется. На каком расстоянии от места бросания оно упадет на землю? Какое время он будет в движении?

Решение. Горизонтальная и вертикальная составляющие начальной скорости

Движение на участке ОА можно разложить на два простых движения: равномерное по горизонтали и равнозамедленное по вертикали:

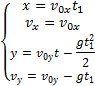
В точке А

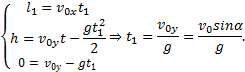
Тогда и

Если тело участвует одновременно в нескольких движениях, то в каждом из них оно участвует независимо от другого, следовательно, время движения на участке АВ определяется временем движения вниз – t₂. Время движения вверх равно времени движения вниз, а, значит,

При равномерном движении по горизонтали за равные промежутки времени тело проходит равные участки пути, следовательно,

Дальность полета

Высота подъема тела

Пример 22. Точка движется прямолинейно на плоскости по закону x=4(t-2)². Каковы начальная скорость v₀ и ускорение точки a? Найти мгновенную скорость точки v_t=5 в начале пятой секунды движения.

Решение.

1) Т.к. v=x’, то v₀=(4∙(t-2)²)’=(4∙(t²-4t+4))’=(4t²-16t+16)’=8t-16

при t=0 v₀=-16 м/с.

2) Т.к. a=, то a=(8t-16)’=8 м/с.

3) При t=4, т.к. до начала 5 с прошло 4 с.

v_t=5=8t-16=8∙4-16=32 м/с.

Ответ: Начальная скорость точки v₀=-16 м/с, ускорение a=8 м/с, скорость точки в начале пятой секунды движения v_t=5=32 м/с.

Пример 23. Движение материальной точки описывается уравнениями: а) s=αt³; б) s=αt²+βt. Сравните среднюю скорость и среднеарифметическую начальной и конечной скоростей v_ср в интервале времени 0 - t. Здесь α и β - положительные постоянные.

Решение. Вспомним определения средней и мгновенной скорости:

Выражения для мгновенной скорости получаются путем дифференцирования уравнения движения.

Выражения для средней скорости находятся как отношение изменения криволинейной координаты к времени:

Получим выражения для среднеарифметической скорости:

Ответим на вопрос условия задачи. Видно, что в случае “а” средняя и среднеарифметическая скорости не совпадают, а в случае “б” - совпадают.

Пример 24. Материальная точка движется равномерно по криволинейной траектории. В какой точке траектории ускорение максимально?

Решение. При движении по криволинейной траектории ускорение складывается из тангенциального и нормального. Тангенциальное ускорение характеризует быстроту изменения величины (модуля) скорости. Если величина скорости не изменяется, тангенциальное ускорение равно нулю. Нормальное ускорение зависит от радиуса кривизны траектории a_n=v²/R. Ускорение максимально в точке с наименьшим радиусом кривизны, т.е. в точке С.

Пример 25. Материальная точка движется согласно закону:

1) Определить начальную координату, начальную скорость и ускорение путем сравнения с законом движения с постоянным ускорением. Записать уравнение для проекции скорости.

Решение. Закон движения с постоянным ускорением имеет вид

Сравнивая это уравнение с уравнением условия задачи, получаем

x₀ = - 1 м,

v_0x = 1 м/с,

a_x = - 0,25 м/с².

Возникает вопрос: какой смысл имеет знак “минус”? Когда проекция вектора отрицательна? Только в том случае, когда вектор направлен против оси координат.

Изобразим на рисунке начальную координату, векторы скорости и ускорения.

Запишем уравнение для скорости в виде

и подставим в него полученные данные (начальные условия)

2) Найти зависимость скорости и ускорения от времени, применяя определения этих величин.

Решение. Применим определения для мгновенных значений скорости и ускорения:

Производя дифференцирование, получим v_x=1-0,25t, a_x = - 0,25 м/с².

Видно, что ускорение не зависит от времени.

3) Построить графики v_х(t) и a_х(t). Охарактеризовать движение на каждом участке графика.

Решение. Зависимость скорости от времени - линейная, график представляет собой прямую линию.

При t = 0 v_х = 1 м/с. При t = 4 с v_х = 0.

Из графика видно, что на участке “а” проекция скорости положительная, а ее величина убывает, т.е. точка движется замедленно в направлении оси х. На участке “b” проекция скорости отрицательная, а ее модуль возрастает. Точка движется ускоренно в направлении, противоположном оси х. Следовательно, в точке пересечения графика с осью абсцисс происходит поворот, изменение направления движения.

4) Определить координату точки поворота и путь до поворота.

Решение. Еще раз отметим, что в точке поворота скорость равна нулю. Для этого состояния из уравнений движения получаем:

Из второго уравнения получаем t_пов = 4 с. (Видно, чтобы получить это значение не обязательно строить и анализировать график). Подставим это значение в первое уравнение: x_пов=-1+4-4²/8 = 1 м. Изобразим, как двигалась точка.

Путь до поворота, как видно из рисунка, равен изменению координаты: s_пов=x_пов-x₀=1-(-1)=2 м.

5) В какой момент времени точка проходит через начало координат?

Решение. В уравнении движения следует положить х = 0. Получаем квадратное уравнение 0=-1+t-t²/8 или t²-8t+8=0. У этого уравнения два корня: 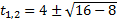. t₁ = 1,17 с, t₂ = 6,83 с. Действительно, точка проходит через начало координат два раза: при движении “туда” и “обратно”.

6) Найти путь, пройденный точкой за 5 секунд после начала движения, и перемещение за это время, а также среднюю путевую скорость на этом участке пути.

Решение. Прежде всего найдем координату, в которой оказалась точка после 5 секунд движения и отметим ее на рисунке.

x(5)=-1+5-5²/8= 0,875 м.

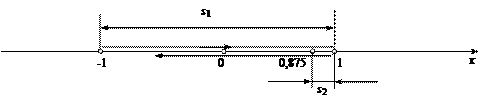
Поскольку в данном состоянии точка находится после поворота, то пройденный путь уже не равняется изменению координаты (перемещению), а складывается из двух слагаемых: пути до поворота

s₁ = x_пов - x₀ = 1 - (-1) = 2 м

и после поворота

s₂ = x_пов - x(5) = 1 - 0,875 = 0,125 м,

s = s₁ + s₂ = 2,125 м.

Перемещение точки равно

s_х = x(5) - x₀ = 0,875 - (-1) = 1,875 м

Средняя путевая скорость вычисляется по формуле

В рассмотренной задаче описан один из наиболее простых видов движения - движение с постоянным ускорением. Тем не менее, данный подход к анализу характера движения является универсальным.

Пример 26. При одномерном движении с постоянным ускорением зависимости координаты и скорости частицы от времени описываются соотношениями:

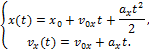
Установить связь между координатой частицы и ее скоростью.

Решение. Из этих уравнений исключаем время t. Для этого используем метод подстановки. Из второго уравнения выражаем время 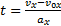и подставляем в первое уравнение:

Если движение начинается из начала координат (х₀ =0) из состояния покоя (v_0x =0), то полученная зависимость принимает вид

хорошо знакомый из школьного курса физики.

Пример 27. Движение материальной точки описывается уравнением: , где i и j - орты осей х и у, α и β - положительные постоянные. В начальный момент времени частица находилась в точке х₀ =у₀=0. Найти уравнение траектории частицы у(х).

Решение. Условие задачи сформулировано с применением векторного способа описания движения. Перейдем к координатному способу. Коэффициенты при единичных векторах представляют собой проекции вектора скорости, а именно:

Вначале получим зависимости x(t) и y(t), решая задачу первого класса.

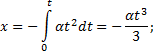
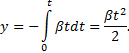
Из полученных уравнений исключим время t. Из первого уравнения . Из второго уравнения получаем

Обратим внимание, что координата х должна быть отрицательной, что соответствует положительным значениям времени t.

Пример 28. Частица движется в положительном направлении оси x так, что ее скорость меняется по закону , где α - положительная постоянная. Учитывая, что в момент времени t = 0 она находилась в начале координат (x₀ = 0), найти зависимость от времени скорости частицы.

Решение. Установим уравнения, связывающие v и x.

По условию задачи . В тоже время можно записать .

Отсюда (ее исключить проще всего). Получилось дифференциальное уравнение с разделяющимися переменными.

Разделяя переменные и интегрируя от 0 до t и от 0 до х, , получаем: , откуда находим зависимость координаты от времени

Искомую зависимость скорости от времени можно получить, применяя любое из двух исходных уравнений. Например,

Пример 29. Частица движется в положительном направлении оси x так, что ее ускорение меняется по закону a=α-βx, где α и β - положительные постоянные. Учитывая, что в момент времени t = 0 она покоилась и находилась в начале координат (x₀ = 0), найдем зависимость скорости частицы от координаты.

Решение. Установим уравнения, связывающие а и x.

a=α-βx, (1)

В эти три уравнения входят четыре переменных: x, v, a, t. Исключим a и t. Выразим из (2) и подставим в (3):

С учетом выражения (1) получаем дифференциальное уравнение

Разделяя переменные

и производя интегрирование

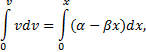
получаем

Искомая зависимость скорости от координаты имеет вид

Пример 30. С башни высотой h бросили камень со скоростью v₀ под углом α к горизонту. Найти:

1) какое время камень будет в движении;

2) на каком расстоянии s он упадет на землю;

3) с какой скоростью он упадет на землю;

4) какой угол β составит траектория камня с горизонтом в точке его падения;

5) нормальное и тангенциальное ускорения камня в этой точке, а также радиус кривизны траектории;

6) наибольшую высоту подъема камня.

Сопротивлением воздуха пренебречь.

Решение. На примере этой задачи покажем, как в обобщенном виде можно установить приведенный алгоритм решения любой задачи данного класса.

1. В задаче рассматривается движение материальной точки (камня) в поле силы тяжести Земли. Следовательно, это движение с постоянным ускорением свободного падения g, направленным вертикально вниз.

2. Движение камня рассматривается относительно наблюдателя, находящегося на земле. Движение двумерное - по горизонтали и вертикали. Применим координатный способ описания. Начало координат поместим на поверхности земли, ось х направим горизонтально, ось у - вертикально вверх.

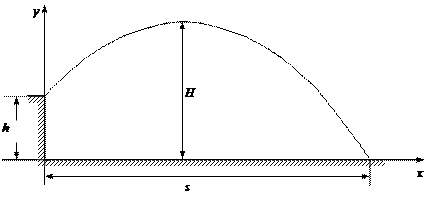
3. В условии задачи рассматривается начальное состояние, состояние А, соответствующее моменту непосредственно перед ударом камня о землю, и состояние В, соответствующее наивысшей точке траектории. Изобразим эти состояния на рисунке и нарисуем векторы скорости в каждом состоянии. Поскольку применяется координатный способ описания, каждый вектор разложим на составляющие. Как было отмечено ранее, вектор ускорения во всех состояниях одинаков и равен g.

4. Движение с постоянным ускорением описывается хорошо известными уравнениями:

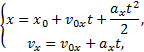
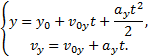
Конкретизируем их для данной задачи. По оси х камень движется из начала координат без ускорения (равномерно) со скоростью v_0x. По оси y камень движется из точки с координатой h с ускорением свободного падения, направленным против оси у и с начальной скоростью v_0у. Отразим эти данные в начальных условиях

x₀=0, v_0x=v₀cosα, a_x=0,

y₀=h, v_0y=v₀sinα, a_y=-g.

и подставим их в уравнения движения.

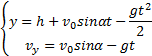
5A. Рассмотрим состояние А. В этом состоянии камень оказался спустя t_A секунд после начала движения. Координаты этой точки равны х_А = s, у_А = 0. На рисунке указаны вектор скорости в этой точке v_A (направленный по касательной к траектории) и его составляющие. Применим уравнения движения к данному состоянию:

В эти четыре уравнения входят следующие неизвестные: t_A , s, v_Аx и v_Аy.

6А. Разрешим полученную систему уравнений относительно указанных неизвестных. Видно, что в уравнение (3) входит одна неизвестная величина - t_A. Решим это квадратное уравнение, преобразовав его предварительно к приведенному виду:

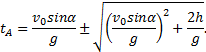
Проанализируем полученный результат. Время не может быть отрицательным, следовательно, отрицательный корень не имеет смысла. Поэтому

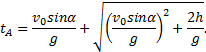
Уравнения (1), (2), (4) позволяют найти все оставшиеся величины: s, v_Аx и v_Аy. Модуль скорости выразим по теореме Пифагора

Из рисунка видно, что

Чтобы найти нормальную и тангенциальную составляющие вектора ускорения, разложим вектор g.

Из рисунка видно, что

Учитывая, что нормальное ускорение связано с модулем скорости соотношением

выразим радиус кривизны траектории в данной точке:

5В. Рассмотрим состояние В. В этом состоянии камень оказался спустя t_В секунд после начала движения. Координаты этой точки равны х_В, у_В = H. На рисунке указан вектор скорости в этой точке v_В, направленный горизонтально по оси х. Следовательно, вертикальная составляющая скорости равна нулю v_Вy =0. Применим уравнения движения к данному состоянию:

Время t_В найдем из уравнения (4)

а максимальную высоту подъема - из уравнения (3)

Видно, что уравнения (1) и (2) не потребовались при решении этой задачи.

Пример 31. Трамвай движется прямолинейно от остановки А до следующей остановки В с ускорением, меняющимся по закону a=α-βx, где α и β - положительные постоянные, х - расстояние между трамваем и остановкой А. Найти расстояние между остановками и максимальную скорость трамвая.

Решение. Решим задачу в соответствии с установленным алгоритмом.

1) Трамвай можно считать материальной точкой, которая движется по прямолинейной траектории. Отличительной чертой его движения является заданная в условии задачи зависимость ускорения от координаты.

2) Применим координатный способ описания движения. Совместим начало координат с остановкой А. Отметим положение остановки В и тоски С, в которой скорость трамвая максимальна.

3) Установим, какая информация о координатах, скоростях, ускорениях содержится в условии задачи, какую требуется определить. В начальном и конечном состояниях скорости равны нулю, а в состоянии С скорость максимальна, поэтому ускорение (производная скорости по времени) равно нулю.

Состояния объекта и их характеристики	Точка А t = 0	Точка С t = tC	Точка В t = tB
Координаты	x0 = 0	-	xB = s - ?
Скорости	v0 = 0	vC = vmax - ?	vB = 0
Ускорения	-	aC = 0	-

4) В условии задана зависимость ускорения от координаты

a=α-βx, (1)

известны или требуют нахождения значения координаты и скорости в состояниях В и С. Следовательно, необходимо уравнение, связывающее v и x.

5) Применим кинематические уравнения к состоянию В. Подставим в уравнение (2) соответствующие значения координаты и скорости

Поскольку в состоянии В s≠0, то 2α-βs=0, откуда

Применим кинематические уравнения к состоянию С. Подставим в уравнения (1) и (2) соответствующие значения координаты и ускорения.

a_C=0=α-β∙x_C, (1a)

Из (1а) выразим координату точки С

и подставим в уравнение (2а):

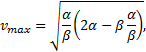
Откуда

Вопросы для самопроверки

- Что изучает кинематика?

- Какие задачи решает кинематика точки и твердого тела?

- В чем различие между телом отсчета и системой отсчета?

- Что понимают под системой отсчета? системой координат? радиус-вектором?

- Дайте определение основных кинематических характеристик движения.

- Что такое "алгебраическая" скорость точки? В каком направлении происходит движение точки при положительном и отрицательном значении алгебраической скорости?

- В чем отличие естественных осей координат от декартовых?

- Какие кинематические величины зависят от выбора системы отсчета? одинаковы в различных системах отсчета?

- Может ли человек, находясь на движущемся эскалаторе метро, быть в покое в системе отсчета, связанной с поверхностью Земли?

- Совпадает ли направление ускорения с направлением скорости материальной точки при равноускоренном движении? при равнозамедленном движении?

- Какие кинематические характеристики движения остаются постоянными при равномерном прямолинейном движении? при равноускоренном движении?

- Какие величины, характеризующие движение, можно определить по графику скорости?

- Два поезда идут навстречу друг другу; один ускоренно на север, другой замедленно на юг. Как будут направлены векторы ускорений поездов?

- Чем отличаются движения, уравнения которых приведены x₁=3-5t-2t²; x₂=-3+5t-2t²?

- Какие существуют способы описания движения материальной точки?

- Перечислите основные способы задания движения точки.

- Дайте определение скорости и ускорения точки при векторном способе задания ее движения.

- Дайте определение скорости и ускорения точки при координатном способе задания ее движения.

- Как определяется характер движения точки при векторном способе задания ее движения?

- Как определяется характер движения точки при координатном способе задания ее движения?

- Каковы условия ускоренного, замедленного движения точки при естественном способе задания ее движения?

- Запишите и покажите на рисунке связь между векторами полного, нормального и касательного ускорений.

- Движение точки задано в полярной системе координат. Как найти уравнение ее траектории?

- Что должно быть известно при естественном способе задания движения точки?

- Какие кинематические способы задания движения точки существуют и в чем состоит каждый из этих способов?

- Запишите в общем виде закон движения в естественной и координатной форме?

- Как разложить вектора скорости и ускорения точки по осям естественного трехгранника?

- Запишите формулы для скорости, касательного и нормального ускорений точки через дуговую координату.

- Как найти проекции ускорения точки на оси естественной системы координат?

- Что называют траекторией движения?

- Как определяется скорость движения при естественном способе задания движения?

- В чем различие понятий "путь" и "дуговая координата"?

- Запишите формулы для определения касательного, нормального и полного ускорений.

- При каких условиях вектор полного ускорения совпадает с вектором: а) нормального ускорения; б) касательного ускорения?

- Что характеризует касательное ускорение и как оно направлено по отношению к вектору скорости?

- Чему равно скалярное произведение векторов скорости и нормального ускорения точки?

- При каких условиях значение дуговой координаты точки в некоторый момент времени равно пути, пройденному точкой за промежуток от начального до данного момента времени?

- Чем является траектория точки при векторном способе задания движения точки?

- Как по уравнениям движения точки в координатной форме определить ее траекторию?

- Сформулируйте теорему о проекции производной вектора на неподвижные координатные оси.

- Приведите определения соприкасающейся, спрямляющей и нормальной плоскостей.

- Как выбираются направления единичных векторов касательной, нормали и бинормали?

- Запишите формулу для определения модуля вектора кривизны плоской кривой.

- Что называется перемещением точки за фиксированный промежуток времени?

- Как направлена средняя скорость точки за некоторый промежуток времени?

- Какие существуют способы определения скорости движения точки?

- Запишите формулы, определяющие модуль и направление скорости точки при координатном способе задания ее движения.

- Как выражается скорость точки через криволинейную координату при естественном способе задания движения?

- Дайте определение среднего ускорения точки за некоторое время.

- Как выражаются модуль и направляющие косинусы вектора ускорения точки через проекции ускорения на прямоугольные координатные оси?

- Как классифицируется движение точки по ускорениям?

- В каких случаях движение точки обращаются в нуль: а) касательное ускорение; б) нормальное ускорение; в) полное ускорение?

- В какой плоскости расположено ускорение точки и чему равны его проекции на естественные координатные оси?

- Как найти проекции ускорения точки на оси неподвижной системы координат Декарта?

- Запишите формулы для нормального и касательного ускорений при естественном способе задания движения.

- Чему равен вектор скорости точки в данный момент времени и какое направление он имеет?

- Как связан орт касательной к кривой с радиусом-вектором движущейся точки?

- Чему равна проекция скорости точки на касательную к ее траектории и модуль ее скорости?

- Как определяются проекции скорости точки на неподвижные оси декартовых координат?

- Что представляет собой годограф скорости и каковы его параметрические уравнения?

- Какой вид имеет годограф скорости прямолинейного неравномерного движения и равномерного движения по кривой, не лежащей в одной плоскости?

- Чему равен вектор ускорения точки и как он направлен по отношению к годографу скорости?

- Как направлены естественные координатные оси в каждой точке кривой?

- Каковы модуль и направление вектора кривизны кривой в данной точке?

- В какой плоскости расположено ускорение точки и чему равны его проекции на естественные координатные оси?

- Что характеризует собой касательное и нормальное ускорения точки?

- При каком движении точки равно нулю касательное ускорение и при каком - нормальное ускорение?

- Как классифицируются движения точки по ускорениям?

- В какие моменты времени нормальное ускорение в криволинейном движении может обратиться в нуль?

- В какие моменты времени касательное ускорение в неравномерном движении может обратиться в нуль?

- Чем отличается график пути от графика движения точки?

- Как по графику движения определить алгебраическое значение скорости точки в любой момент времени?

- Как по графику скорости прямолинейного движения точки определить алгебраическое значение ускорения точки в любой момент времени?

- Запишите формулу ускорения при прямолинейном движении?

- Запишите формулу ускорения (полного) при криволинейном движении.

- Сравните время падения тела, брошенного горизонтально с некоторой высоты и свободно падающего с той же высоты.

- Три тела брошены так: первое — вниз без начальной скорости, второе — вниз с начальной скоростью, третье — вверх. Что можно сказать об ускорениях этих тел при их движении?

- Как будет изменяться дальность полета снарядов при увеличении угла наклона орудия к горизонту?

- Как направлено ускорение при криволинейном движении?

- Как направлена мгновенная скорость материальной точки при криволинейном движении?

- Является ли движение по окружности с постоянной по модулю скоростью равноускоренным?

- Автомобиль движется на повороте. Одинаковые ли расстояния проходят при этом правые и левые колеса автомобиля?

- Велосипедист движется по прямолинейному участку дороги со скоростью (см.рис.). С какой скоростью движутся точки А, В, С, D колеса велосипеда относительно оси? относительно дороги?

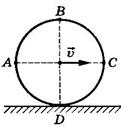
- Два велосипедиста движутся навстречу друг другу. Модуль скорости первого велосипедиста увеличивается, а модуль скорости второго — уменьшается. Различаются ли направления ускорений велосипедистов относительно дороги?

- Как направлен вектор ускорения в случаях аи б,представленных на рисунке?

- Выразите в радианах угол поворота часовой стрелки за 1 ч, 3 ч, 6 ч, 12 ч, 24 ч.

- Колесо вращается вокруг неподвижной оси, проходящей через его центр. Обладает ли любая точка на ободе колеса тангенциальным и нормальным ускорениями, если вращение происходит с постоянной угловой скоростью? с постоянным угловым ускорением?

- Катер со спортсменом на водных лыжах движется по окружности. Спортсмен может следовать за ним по той же окружности, а также вне и внутри этой окружности. Каково соотношение скоростей спортсмена и катера в этих случаях?

- Частица движется вдоль оси OX,проходя за каждую секунду по одному метру. Будет ли движение частицы равномерным?

- На рисунке представлены графики зависимости координат тел от времени. Напишите уравнения движения тел. Нарисуйте графики v_x(t).

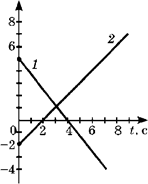
- Два тела одновременно начинают двигаться прямолинейно. Уравнения их движения имеют вид: х₁=6-2t; х₂=4t (величины, входящие в уравнение, заданы в СИ).

1) Нарисуйте траектории движения тел.

2) Определите время встречи и координату местав стречи тел.

3) Нарисуйте графики v_1x(t), v_2x(t), x₁(t), x₂(t).

- По заданному уравнению движения точки S=25+1,5t+6t² определите вид движения и без расчетов, используя законы движения точки, ответьте, чему равны начальная скорость и ускорение?

- По заданному уравнению движения точки S=22t-4t² постройте графики скорости и касательного ускорения?

- Задано уравнение движения тела S=f(t). Как определяют скорость и ускорение?

- Для заданного закона (уравнения) движения φ=2,28+12t+3t² определите угловое ускорение в момент времени t=5 с?

- Определите модуль и направление полной скорости точки, если заданы проекции скорости на оси координат: v_x=3 м/с, v_y=4 м/с.

- Какое движение точки называется гармоническим колебательным движением и какие величины характеризуют это движение?

- Как направлено ускорение гармонического колебательного движения? В какие промежутки времени это движение происходит ускоренно и в какие – замедленно?

- Основная задача кинематики:

1) установить закон механического движения;

2) определить поступательное движение;

3) определить вращательное движение;

4) определить плоскопараллельное движение;

5) определить сложное движение.

- Какая величина является векторной

1) масса;

2) длина траектории;

3) перемещение;

4) время движения;

5) нет правильного ответа.

- Какая величина является векторной

1) масса;

2) длина траектории;

3) работа;

4) время движения;

5) нет правильного ответа.

- Какие из перечисленных ниже величин являются векторными?

1) путь;

2) скорость;

3) масса;

4) все перечисленные величины векторные.

- Какая величина является скалярной

1) сила;

2) перемещение;

3) ускорение;

4) скорость;

5) нет правильного ответа.

- Какая величина является скалярной

1) сила;

2) длина траектории;

3) ускорение;

4) скорость;

5) перемещение.

- Укажите в каких нижеследующих случаях тело можно принять за материальную точку?

1) при установке ракеты на старте;

2) при расчете траектории ракеты;

3) при расчете угловой скорости суточного вращения Земли вокруг оси.

- Понятие «длины пути»:

1) длина расстояния, пройденного точкой вдоль траектории;

2) кривая линия, образованная точками пространства, через которые движется точка;

3) прямая линия, соединяющая начальную и конечную точку траектории.

- Каким образом направлен вектор скорости точки в данный момент времени?

1) вектор скорости направлен по нормали к траектории;

2) вектор скорости направлен вдоль хорды в сторону движения точки;

3) вектор скорости направлен по касательной к траектории в сторону движения.

- Понятие траектории:

1) векторная величина, соединяющая начало и конец пути;

2) прямая линия, соединяющая начало и конец пути;

3) расстояние от начала координат до конца перпендикуляра, опущенного на координатную ось из рассматриваемой точки;

4) перемещение точки;

5) кривая линия, образованная точками пространства, через которые пройдет движущаяся точка.

- Можно ли определить траекторию движения точки, если известно, как изменяются во времени координаты точки в прямоугольной системе координат (например x=at²; y=bt²)?

1) можно;

2) нельзя.

- Можно ли только по заданной траектории точки определить пройденный ее путь?

1) можно;

2) нельзя.

- Перемещение:

1) направленный отрезок прямой, соединяющий начальное положение точки с последующим;

2) линия, вдоль которой движется материальная точка;

3) кривая, которую описывает конец вектора скорости;

4) изменение скорости за время;

5) изменение перемещения за малое время.

- Точка движется по прямой с постоянным ускорением, направленным противоположно скорости. Определить, как движется точка?

1) равномерно;

2) равномерно-ускоренно;

3) равномерно-замедленно.

- Какая составляющая ускорения точки характеризует изменение значения скорости?

1) нормальное ускорение;

2) касательное ускорение.

- Эскалатор в метрополитене поднимается со скоростью 1 м/с. Может ли человек, находящийся на нем, быть в состоянии покоя в системе отсчета, связанной с Землей?

1) может, если движется в противоположную сторону со скоростью 1 м/с;

2) может, если движется в ту же сторону со скоростью 1 м/с;

3) может, если стоит на эскалаторе;

4) не может ни при каких условиях.

- Два автомобиля движутся в одном направлении по прямому шоссе с одинаковыми скоростями v. Чему равна скорость первого автомобиля относительно второго?

1) 0;

2) v;

3) -v.

- Направление мгновенной скорости:

1)

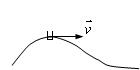
2)

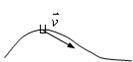
3)

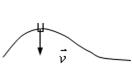
4)

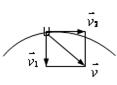
5)

- На рисунках изображены графики зависимости модуля ускорения от времени для разных видов движения. Какой из графиков соответствует равномерному движению?

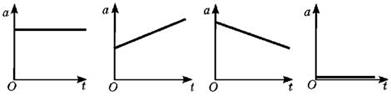
1) 1;

2) 2;

3) 3;

4) 4.

- Формула мгновенной скорости.

1)

2)

3)

4)

5)

- Формула модуля скорости через составляющие.

1)

2)

3)

4)

5)

- Значение скорости в данный момент времени.

1)

2)

3)

4)

5)

- Формула тангенциального ускорения.

1)

2)

3)

4)

5)

- Формула нормального ускорения.

1)

2)

3)

4)

5)

- Автомобиль, трогаясь с места, движется с ускорением 3 м/с². Через 4 с скорость автомобиля будет равна:

1) 12 м/с;

2) 0,75 м/с;

3) 48 м/с;

4) 6 м/с.

- Зависимость координаты от времени для некоторого тела описывается уравнением х=8t-t². В какой момент времени проекция скорости тела на ось ОХ будет равна нулю?

1) 8 с;

2) 4 с;

3) 3 с;

4) 0 с.

- От высокой скалы откололся и стал свободно падать камень. Какую скорость он будет иметь через 3 с после начала падения?

1) 30 м/с;

2) 10 м/с;

3) 3 м/с;

4) 2 м/с.

- Стрела пущена вертикально вверх. Проекция ее скорости на вертикальное направление меняется со временем согласно графику на рисунке. В какой момент времени стрела достигла максимальной высоты?

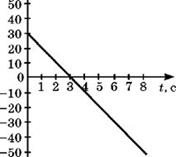
1) 1,5 с;

2) 3 с;

3) 4,5 с;

4) 6 с.

- Трамвайный вагон движется на повороте по закруглению радиусом 40 м. Рассчитайте скорость трамвая, если центростремительное ускорение равно 0,4 м/с².

1) 2 м/с;

2) 1 м/с;

3) 4 м/с;

4) 5 м/с.

- Какова частота вращения тела, движущегося по окружности радиусом 5 м со скоростью 5 м/с?

1) 2 Гц;

2) 0,5 Гц;

3) 4 Гц;

4) 0,2 Гц.

- Плот равномерно плывет по реке со скоростью 6 км/ч. Человек движется поперек плота со скоростью 8 км/ч. Чему равна скорость человека в системе отсчета, связанной с берегом?

1) 10 км/ч;

2) 7 км/ч;

3) 14 км/ч;

4) 2 км/ч.

- Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 7-ой секунды, считая, что характер движения тела не изменится.

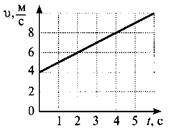
1) 8 м/с;

2) 11 м/с;

3) 16 м/с;

4) 18 м/с.

- На рисунке представлена зависимость проекции скорости тела от времени. Модуль ускорения имеет максимальное значение на участке

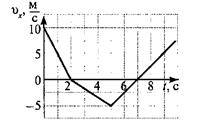
1) от 0 с до 2 с;

2) от 2 с до 5 с;

3) от 2 с до 7 с;

4) ускорение на всех участках одинаково.

- Зависимость пути от времени для прямолинейно движущегося тела имеет вид: S(t)=2t+t², где все величины выражены в СИ. Ускорение тела равно

1) 1 м/с²;

2) 2 м/с²;

3) 3 м/с²;

4) 6 м/с².

- На рисунке представлен график зависимости проекции скорости тела от времени. Какой путь прошло тело за интервал времени от 2 до 8 с?

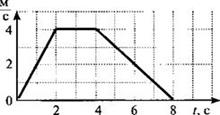
1) 32 м;

2) 20 м;

3) 16 м;

4) 8 м.

- Тело упало с некоторой высоты с нулевой начальной скоростью и при ударе о землю имело скорость 40 м/с. Чему равно время падения? Сопротивлением воздуха пренебречь.

1) 0,25 с;

2) 4 с;

3) 40 с;

4) 400 с.

- Материальная точка движется по окружности с постоянной скоростью. Как изменится центростремительное ускорение точки, если скорость увеличить в 2 раза и радиус окружности увеличить в 2 раза;

1) уменьшится в 2 раза;

2) увеличится в 2 раза;

3) увеличится в 4 раза;

4) уменьшится в 8 раз.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00