Главная
Лекция 4. Сложное движение точки и тела
В данной лекции
рассматриваются следующие вопросы:
1.
Сложное движение точки.
2.
Относительное, переносное и абсолютное движения.
3.
Теорема сложения скоростей.
4.
Теорема сложения ускорений. Ускорение Кориолиса.
5.
Сложное движение твердого тела.
6.
Цилиндрические зубчатые передачи.
7.
Сложение поступательного и вращательного движений.
8.
Винтовое движение.
Изучение данных вопросов необходимо в
дальнейшем для динамики плоского движения твердого тела, динамики
относительного движения материальной точки, для решения задач в дисциплинах
«Теория машин и механизмов» и «Детали машин».
Сложное
движение точки.
Относительное, переносное и абсолютное движения.
До сих пор мы изучали движение точки или тела по
отношению к одной заданной системе отсчета. Однако в ряде случаев при решении
задач механики оказывается целесообразным (а иногда и необходимым)
рассматривать движение точки (или тела) одновременно по отношению к двум системам отсчета, из
которых одна считается основной или условно неподвижной, а другая определенным
образом движется по отношению к первой. Движение, совершаемое при этом точкой (или телом), называют составным
или сложным. Например, шар, катящийся по палубе движущегося
парохода, можно считать совершающим по отношению к берегу сложное движение,
состоящее из качения по отношению к палубе (подвижная система отсчета), и
движение вместе с палубой парохода по отношению к берегу (неподвижная система
отсчета). Таким путем сложное движение шара разлагается на два более простых и
более легко исследуемых.
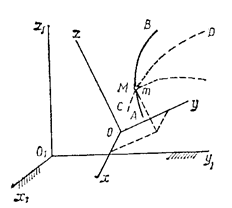
Рис.1
Рассмотрим точку М,
движущуюся по отношению к подвижно
системе отсчета Oxyz, которая в свою очередь как-то движется относительно
другой системы отсчета O1x1y1z1, которую
называем основной или условно неподвижной (рис.1). Каждая из этих систем
отсчета связана, конечно, с определенным телом, на чертеже не показанным. Введем
следующие определения.
1. Движение, совершаемое точкой М по отношению к подвижной системе отсчета (к осям Oxyz), называется относительным движением (такое
движение будет видеть наблюдатель, связанный с этими осями и перемещающийся
вместе с ними). Траектория АВ,
описываемая точкой в относительном движении, называется относительной
траекторией. Скорость точки М по
отношению к осям Oxyz называется относительной скоростью (обозначается 
), a ускорение -
относительным ускорением (обозначается 
). Из определения следует, что при вычислении 
и можно движение
осей Oxyz
во внимание не принимать (рассматривать их как неподвижные).
2. Движение, совершаемое подвижной системой отсчета Oxyz (и всеми неизменно связанными с нею точками
пространства) по отношению к неподвижной системе O1x1y1z1,
является для точки М переносным движением.
Скорость той неизменно связанной с подвижными осями Oxyz точки m, с которой в данный момент времени совпадает движущаяся точка М, называется переносной скоростью точки
М в этот момент (обозначается 
), а ускорение этой точки m - переносным ускорением точки М (обозначается 
). Таким образом,
Если представить себе, что относительное движение
точки происходит по поверхности (или внутри) твердого тела, с которым жестко
связаны подвижные оси Oxyz,
то переносной скоростью (или ускорением) точки М в данный момент времени будет скорость (или ускорение) той точки
т тела, с которой в этот момент совпадает точка М.
3. Движение, совершаемое точкой по отношению к
неподвижной системе отсчета O1x1y1z1, называется абсолютным или сложным. Траектория CD этого
движения называется абсолютной траекторией, скорость - абсолютной скоростью (обозначается 
) и ускорение - абсолютным ускорением (обозначается 
).
В приведенном выше примере движение шара относительно
палубы парохода будет относительным, а скорость - относительной скоростью
шара; движение парохода по отношению к берегу будет для шара переносным
движением, а скорость той точки палубы, которой в данный момент времени касается шар будет в этот момент его переносной скоростью;
наконец, движение шара по отношению к берегу будет его абсолютным движением, а
скорость - абсолютной скоростью шара.
При исследовании
сложного движения точки полезно применять «Правило остановки». Для того, чтобы неподвижный наблюдатель увидел относительное
движение точки, надо остановить переносное движение.
Тогда будет происходить
только относительное движение. Относительное
движение станет абсолютным. И наоборот, если остановить
относительное движение, переносное станет абсолютным и неподвижный наблюдатель увидит только это
переносное движение.
В
последнем случае, при
определении переносного движения точки, обнаруживается одно очень важное
обстоятельство. Переносное движение точки зависит от того в какой момент будет
остановлено относительное движение, от
того, где точка находится
на среде в этот момент. Так как, вообще говоря, все
точки среды движутся по-разному. Поэтому логичнее определять переносное
движение точки как абсолютное движение той точки среды, с которой совпадает в
данный момент движущаяся точка.
Teopeмa сложения скоростей.
Пусть некоторая точка М совершает движение по отношению к системе отсчета Oxyz, которая сама движется произвольным образом по
отношению к неподвижной системе отсчета O1x1y1z1,
(рис.2).
Конечно, абсолютное
движение точки М
определяется уравнениями
Относительное движение – в движущихся осях
уравнениями
Рис. 10.3.
Уравнений,
определяющих переносное движение
точки, не может быть вообще.
Так как, по определению,
переносное движение точки М –
это движение относительно
неподвижных осей той
точки системы O1x1y1z1, с которой
совпадает точка в данный момент.
Но все точки подвижной системы движутся по-разному.
Положение подвижной системы отсчета может быть также
определено, если задать положение точки О радиусом-вектором 
, проведенным из начала неподвижной системы отсчета, и
направления единичных векторов 
подвижных осей Оx, Oy, Oz.
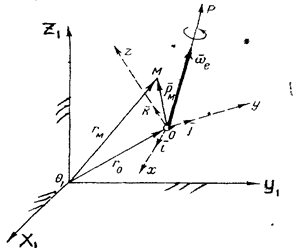
Рис.2
Произвольное переносное движение подвижной системы
отсчета слагается из поступательного движения
со скоростью 
точки О и движения
вокруг мгновенной оси вращения ОР,
походящей через точку О, с мгновенной
угловой скоростью 
. Вследствие переносного движения подвижной системы
отсчета радиус-вектора 
и направления
единичных векторов изменяются.
Если векторы 
заданы в
функции времени, то переносное движение подвижной системы отсчета вполне определено.
Положение точки М
по отношению к подвижной системе отсчета можно определить радиусом-вектором
,
где координаты x,
y, z точки М изменяются с
течением времени вследствие движения точки М
относительно подвижной системы отсчета. Если радиус-вектор задан в функции
времени, то относительное движение точки М,
т.е. движение этой точки относительно подвижной системы отсчета, задано.
Положение точки М относительно неподвижной системы
отсчета O1x1y1z1, может
быть определено радиусом-вектором 
. Из рис.2 видно, что
. (1)
Если относительные координаты x,y,z точки М и векторы определены в функции времени, то слагающееся
из относительного и переносного движений составное движение точки М, т.е. движение этой точки по отношению
к неподвижной системе отсчета, также
надо считать заданным.
Скорость составного движения точки М, или абсолютная скорость этой точки,
равна, очевидно, производной от радиуса-вектора точки M по времени t
Поэтому, дифференцируя равенство (1) по времени t, получим
Разобьем слагаемые в правой части этого равенства на
две группы по следующему признаку. К
первой группе отнесем те слагаемые, которые содержат производные только от
относительных координат x,y,z, а ко второй - те слагаемые, которые содержат
производные от векторов , т.е. от величин, изменяющихся только вследствие
переносного движения подвижной системы отсчета
Каждая из групп слагаемых, обозначенных через и 
, представляет собой, по крайней мере, по размерности
некоторую скорость. Выясним физический смысл скоростей
и .
Скорость , как это следует из равенства (3), вычисляется в
предположении, что изменяются только относительные координаты x,y,z точки М, но векторы остаются постоянными,
т.е. подвижная система отсчета Oxyz как бы условно считается неподвижной. Итак, скорость представляет
собой относительную скорость точки М.
Скорость вычисляется
так, как будто бы точка М не
двигалась относительно подвижной системы отсчета, так как производные x,y,z в
равенство (4) не входят. Поэтому скорость представляет
собой переносную скорость точки М.
Итак, 
. (5)
Это равенство выражает теорему сложения скоростей в случае,
когда переносное движение является произвольным: абсолютная скорость точки М равна геометрической сумме переносной
и относительной скоростей этой точки.
Пример 1. Колечко М движется по вращающемуся стержню (рис.3) так, что OM=s=3t2
(см) и
(рад).
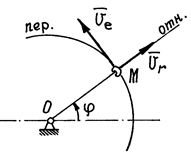
Рис.3
Ранее было
установлено, что траектория
относительного движения –
прямая линия, совпадающая
со стержнем, и движение это определяется
уравнением s=s(t).
Траектория переносного движения
точки М в момент времени t –
окружность радиуса OM=s.
Поэтому
относительная скорость 
. И
направлена по касательной к
траектории вдоль стержня (рис.3). Переносная
скорость колечка, как при вращении вокруг оси, 
. Направлен вектор этой скорости по касательной к
траектории переносного движения, перпендикулярно стержню.
Абсолютная
скорость колечка 
. Величина ее, т.к. 
.
.
Теорема сложения ускорений. Ускорение
Кориолиса.
Ускорение составного движения точки М, или абсолютное ускорение этой точки,
равно, очевидно, производной от абсолютной скорости точки М по времени t
Поэтому, дифференцируя равенство по времени, получим
Разделим слагаемые правой части этого равенства на три группы.
К первой группе отнесем слагаемые, содержащие только
производные от относительных координат x,y и z, но не
содержащие производные от векторов :
Ко второй группе отнесем слагаемые, которые содержат
только производные от векторов 
, но не содержащие производных от относительных
координат x,y,z:
Осталась еще одна группа слагаемых, которые не могли
быть отнесены ни к первой, ни ко второй, так как они содержат производные от всех
переменных x, y, z, . Обозначим эту группу слагаемых через
:
Каждая из выделенных групп представляет собой, по
крайней мере по размерности, некоторое ускорение.
Выясним физический смысл всех трех ускорений: 
.
Ускорение , как это видно из равенства, вычисляется так, как
если бы относительные координаты x,y,z изменялись с течением времени, а векторы оставались
неизменными, т.е. подвижная система отсчета
Oxyz как бы покоилась, а точка М двигалась. Поэтому ускорение 
представляет собой относительное ускорение точки М. Так как ускорение (и скорость) относительного движения
вычисляется в предположении, что подвижная система отсчета находится а покое,
то для определения относительного ускорения (и скорости) можно пользоваться
всеми правилами, изложенными ранее в кинематике точки.
Ускорение , как это видно из равенства, вычисляется в
предположении, что сама точка М
покоится по отношению к подвижной
системе отсчета Oxyz (x =const, y =const, z
=const) и перемещается вместе с этой системой отсчета по
отношению к неподвижной системе отсчета O1x1y1z1. Поэтому
ускорение представляет
собой переносное ускорение точки М.
Третья группа слагаемых определяет ускорение , которое не может быть отнесено не к относительному
ускорению , так как содержит в своем выражении производные 
не к
переносному ускорению , так как содержит в своем выражении производные 
.
Преобразуем правую часть равенства, припомнив, что
Подставляя эти значения производных в равенства,
получим
или 
Здесь вектор 
есть
относительная скорость точки М, поэтому
Ускорение называют ускорением
Кориолиса. Ввиду того, что ускорение Кориолиса появляется в случае
вращения подвижной системы отсчета, его называют еще поворотным ускорением.
С физической точки зрения появление поворотного
ускорения точки объясняется взаимным влиянием переносного и относительного
движений.
Итак, ускорение Кориолиса точки равно по модулю и
направлению удвоенному векторному произведению угловой скорости переносного
движения на относительную скорость точки.
Равенство, которое теперь можно сокращенно записать в
виде
представляет
теорему сложения ускорений в случае, когда переносное движение является
произвольным: абсолютное ускорение точки равно векторной сумме переносного,
относительного и поворотного ускорений. Эту теорему часто называют теоремой
Кориолиса.
Из формулы следует, что модуль поворотного ускорения
будет
где 
- угол между
вектором 
и вектором . Чтобы определить направление поворотного ускорения , нужно мысленно перенести вектор в точку М и руководствоваться правилом векторной
алгебры. Согласно этому правилу, вектор 
нужно
направлять перпендикулярно к плоскости, определяемой векторами и , и так, чтобы, смотря с конца вектора 
, наблюдатель мог видеть кратчайший поворот от к происходящим
против движения часовой стрелки.
Для определения направления можно также
пользоваться следующим правилом Н. Е. Жуковского: чтобы получить направление
поворотного ускорения , достаточно составляющую 
относительной
скорости точки М, перпендикулярную к вектору , повернуть (в
плоскости, перпендикулярной к вектору ) на прямой угол вокруг точки М в направлении переносного вращения (рис.4).
Рис.4
Если переносное движение подвижной системы отсчета
есть поступательное движение, то =0 и поэтому
поворотное ускорение 
точки также равно
нулю. Поворотное ускорение равно, очевидно, нулю и в том случае, когда в данный
момент времени обращается в нуль.
Кроме того, поворотное ускорение точки может,
очевидно, обращаться в нуль, если:
а) вектор относительной скорости точки
параллелен вектору угловой скорости переносного
вращения, т.е. относительное движение точки происходит
по направлению, параллельному оси переносного вращения;
б) точка не имеет движения относительно подвижной
системы отсчета или относительная скорость точки в данный
момент времени равна нулю (
).
Пример 2. Пусть тело вращается вокруг неподвижной оси z. По
поверхности его движется точка М
(рис. 5). Конечно, скорость этого движения точки – относительная скорость , а скорость
вращения тела – угловая скорость переносного движения .
Ускорение Кориолиса 
, направлено перпендикулярно этим двум векторам, по
правилу направления вектора векторного произведения. Так, как показано на
рис. 5.
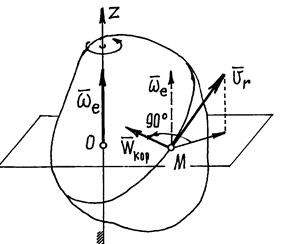
Рис.5
Нетрудно сформулировать более удобное правило определения направления вектора 
: нужно
спроектировать вектор относительной скорости на плоскость
перпендикулярную оси переносного вращения и затем повернуть эту проекцию на
90 градусов в плоскости по направлению переносного вращения. Конечное положение
проекции вектора укажет
направление кориолисова ускорения. (Это правило было
предложено Н.Е. Жуковским).
Пример 3. (Вернемся к примеру 1).
Найдем абсолютное ускорение колечка М:
. (6)
Переносное ускорение при движении колечка по
окружности радиусом OM=s:
, где 
.
Значит 
(рис.6).
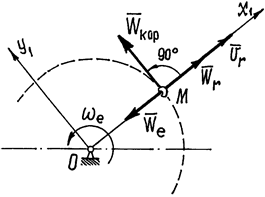
Рис.6
Относительное
ускорение 
.
Ускорение Кориолиса 
.
Вектор 
направлен
перпендикулярно стержню в сторону вращения (по правилу Жуковского).
Рис. 10.7.
Величину абсолютного ускорения
колечка М найдем с помощью проекций на подвижные оси x1 и y1 проектируя
равенство (6) на оси, получим:
Тогда 
Сложное
движение твердого тела.
Так же как при
сложном движении точки
нередко и движение тела можно
рассматривать как сумму
нескольких движений. Например, состоящее из
двух поступательных движений или поступательного движения и вращения
в округ оси. Часто встречаются движения, состоящие из двух вращений вокруг
осей или поступательного движения
и вращения вокруг точки. Исследование
движения точек принадлежащих
телу, совершающему сложное
движение, можно проводить методами, изложенными выше и
никаких особых трудностей не вызывает. Но анализ сложного движения тела,
состоящего из нескольких вращений, обнаруживает некоторые особенности, которые
следует рассмотреть специально.
1.
Сложение вращений тела вокруг двух осей
На рис. 7 изображено тело, которое совершает сложное
движение – вращение вокруг оси, которая сама вращается вокруг другой, неподвижной
оси. Естественно, первое вращение следует назвать относительным движением
тела, второе – переносным, а соответствующие оси обозначить 
.
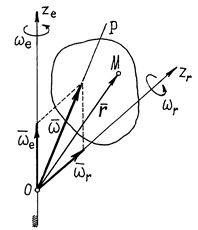
Рис.7
Абсолютным движением будет вращение вокруг точки
пересечения осей О. (Еcли тело имеет
больший размер, то его точка, совпадающая с О, все время будет неподвижной). Угловые
скорости переносного вращения и относительного вращения изображается векторами и 
, отложенными из неподвижной точки О, точки пересечения осей, по
соответствующим осям.
Найдем абсолютную скорость какой-нибудь точки М тела, положение которой определяется радиусом-вектором 
(рис.7).
Как известно, она складывается из двух скоростей, относительной и переносной: 
. Но
относительное движение точки (используя правило остановки), есть вращение с угловой
скоростью вокруг оси 
, определяется радиусом-вектором
. Поэтому, 
.
Рис. 11.1.
Переносное движение точки в
данный момент времени, опять используя
правило остановки, тоже есть вращение, но вокруг оси
с угловой
скоростью и будет
определяться тем же радиусом-вектором 
. Поэтому и переносная скорость r.
Абсолютная же скорость, скорость при вращении вокруг
неподвижной точки О,
при сферическом движении, определяется
аналогично 
, где 
-
абсолютная угловая скорость,
направленная по мгновенной оси вращения Р.
По формуле сложения
скоростей получим: 
или 
.
Отсюда 
То есть мгновенная
угловая скорость, угловая скорость абсолютного движения, есть векторная
сумма угловых скоростей переносного и относительного движений. А мгновенная ось
вращения P, направленная по вектору , совпадает с диагональю параллелограмма, построенного
на векторах и (рис.7).
Частные случаи:
1. Оси вращения 
и 
параллельны, направления вращений одинаковы (рис. 8).
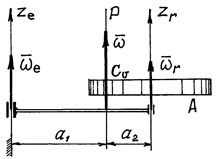
Рис.8
Так как векторы и параллельны и
направлены в одну сторону, то абсолютная
угловая скорость по величине равна сумме их модулей 
и вектор ее
направлен в туже сторону. Мгновенная ось вращения Р делит расстояние между осями на части обратно пропорциональные 
и 
:
.
(аналогично равнодействующей
параллельных сил).
В этом частном
случае тело А
совершает плоскопараллельное движение. Мгновенный центр скоростей 
находится на
оси Р.
2. Оси
вращения параллельны, направления
вращений противоположны (рис.9).
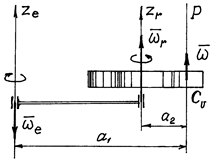
Рис.9
В этом случае 
(при 
).
Мгновенная ось вращения
и мгновенный центр
скоростей находятся за вектором
большей угловой скорости на расстояниях таких, что (опять по
аналогии определения
равнодействующей параллельных сил).
3. Оси
вращения параллельны, направления
вращений противоположны и угловые
скорости равны.
Угловая скорость абсолютного движения 
и,
следовательно, тело совершает поступательное
движение. Этот случай
называется парой вращений, по
аналогии с парой сил.
Пример 4. Диск радиусом R вращается
вокруг горизонтальной оси с угловой скоростью 
, а эта ось вместе с рамкой вращается вокруг вертикальной
неподвижной оси с угловой скоростью (рис.10).
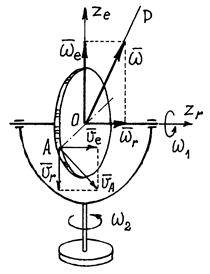
Рис.10
Горизонтальная
ось – это
ось относительного вращения ; вертикальная
ось – ось переносного вращения . Соответственно угловые скорости 
векторы их
направлены по осям и .
Абсолютная угловая скорость , а величина ее, так как 
,
.
Скорость точки А, например, можно найти или как сумму переносной и относительной
скоростей: 
, где 
и 
,
или как при абсолютном движении, при вращении вокруг
мгновенной оси Р,
.
Вектор
скорости 
будет
расположен в плоскости перпендикулярной вектору и оси Р.
Пример 5. Водило ОА с
укрепленными на нем двумя колесами 2 и 3 вращается вокруг оси
О с угловой скоростью 
. Колесо 2 при этом будет обкатываться по неподвижному
колесу 1 и заставит вращаться
колесо 3. Найдем угловую скорость 
, этого колеса. Радиусы колес R1, R2, R3 (рис.11).
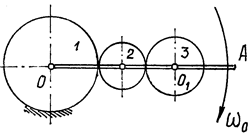
Рис.11
Колесо 3 участвует в
двух движениях. Вращаться вместе с водилом
вокруг оси О
и относительно оси O1. Ось О будет переносной осью, ось O1 – относительной. Переносная угловая
скорость колеса 3 – это угловая
скорость водила 
, направленная
по часовой стрелке, как .
Чтобы
определить угловую скорость
относительного движения, наблюдателю нужно находиться на водиле. Он увидит водило
неподвижным, колесо 1 вращающимся
против часовой стрелки со
скоростью (рис. 12), а
колесо 3 – вращающимся с
относительной угловой скоростью , против часовой
стрелки. Так как 
, то 
. Оси вращения
параллельны, направления вращений
противоположны. Поэтому 
и направлена так же как , против
часовой стрелки. В частности,
если R3=R1, то 
и 
. Колесо 3
будет двигаться поступательно.
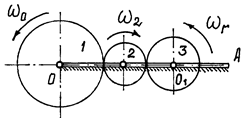
Рис.12
Исследование движения других подобных конструкций
(планетарных и дифференциальных редукторов,
передач) ведется аналогичным
способом.
Переносной
угловой скоростью является
угловая скорость водила (рамки, крестовины
и т.п.), а чтобы определить относительную скорость
какого-либо колеса, нужно
водило остановить, а неподвижное колесо заставить вращаться
с угловой скоростью водила,
но в противоположную сторону.
Угловые
ускорения тела в абсолютном
движении можно искать как производную 
, где . Покажем (рис.13) единичные векторы 
и 
(орты осей и ), а векторы
угловых скоростей запишем так:
.
Тогда 
и угловое
ускорение, при 
,
Рис. 11.7.
Здесь
Поэтому 
или
и 
,
где 
– угловое
ускорение переносного вращения; 
– угловое
ускорение относительного вращения; 
– добавочное
угловое ускорение, которое определяет
изменение относительной угловой
скорости при переносном движении. Направлен этот вектор
перпендикулярно осям и , как скорость
конца вектора . Модуль
добавочного углового ускорения 
, где - угол между
осями.
Конечно, если оси
вращения параллельны, это угловое
ускорение 
будет равно
нулю, так как 
.
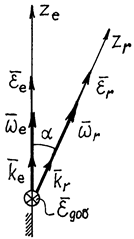
Рис.13
2. Общий
случай движения тела
Произвольное движение тела – это общий случай движения.
Его можно рассматривать как сумму двух движений: поступательного вместе с
произвольно выбранным полюсом С
и вращения вокруг этого полюса.
Первое движение определяется уравнениями движения полюса, точки С:
А второе движение – уравнениями вращения
вокруг точки С с помощью углов Эйлера:
Скорости и ускорения
точек тела в общем случае, при произвольном движении, определяются такими же методами, как при сложном движении
точки (см. раздел выше).
3. Цилиндрические зубчатые передачи.
Рассмотрим основные виды этих передач.
1. Рядовой назовем передачу, в которой все оси колес,
находящихся в последовательном зацеплении, неподвижны. При этом одно из колес (например,
колесо 1 на рис.14) является ведущим, а остальные ведомыми.
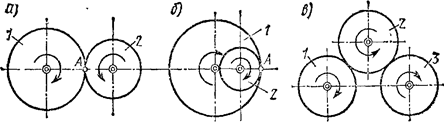
Рис.14
В случае внешнего (рис.14,а) или внутреннего
(рис.14,б) зацепления двух колес имеем 
, так как скорость точки сцепления А у обоих колес одинакова.
Учитывая, что число z зубцов сцепленных колес пропорционально их радиусам, а
вращения колес происходят при внутреннем зацеплении в одну сторону, а при
внешнем в разные, получаем
При внешнем зацеплении трех колес (рис.14, в) найдем,
что
Следовательно, отношение угловых скоростей крайних
шестерен в этой передаче обратно пропорционально их радиусам (числу зубцов) и
не зависит от радиусов промежуточных (паразитных) шестерен.
Из полученных результатов следует, что при рядовом
сцеплении шестерен
где k - число внешних зацеплений (в случае, изображенном на
рис.14,а имеется одно внешнее зацепление; на рис.61, в
- два внешних зацепления, на рис.14,б
внешних зацеплений нет).
Передаточным числом данной зубчатой передачи
называется величина 
, дающая отношение угловой скорости ведущего колеса к
угловой скорости ведомого:
=
2. Планетарной называется передача (рис.15), в которой
шестерня 1 неподвижна, а оси остальных шестерен, находящихся в последовательном
зацеплении, укреплены на кривошипе АВ, вращающемся вокруг оси неподвижной
шестерни.
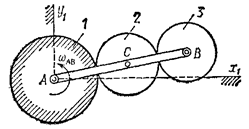
Рис.15
3. Дифференциальной называется передача, изображенная на
рис. 62, если в ней шестерня 1 не является неподвижной и может вращаться вокруг
своей оси А
независимо от кривошипа АВ.
Расчет планетарных и дифференциальных передач можно
производить, сообщив мысленно всей неподвижной плоскости Ах1y1 вращение с угловой скоростью - 
, равной по модулю и противоположной по направлению
угловой скорости кривошипа АВ (метод
остановки или метод Виллиса).
Тогда кривошип в этом сложном движении будет
неподвижен, а любая шестерня радиуса 
будет иметь
угловую скорость
,
где 
- абсолютная
угловая скорость этой шестерни по отношению к осям Ах1y1 (рис.15).
При этом оси всех шестерен будут неподвижны и зависимость
между 
можно будет определить, приравнивая скорости точек сцепления.
Расчет планетарных и дифференциальных передач можно
также производить с помощью мгновенных центров скоростей.
4. Сложение поступательного и вращательного
движений. Винтовое движение.
Если сложное движение тела слагается из вращательного
вокруг оси Аа
с угловой скоростью и
поступательного со скоростью v, направленной
параллельно оси Аа
(рис.16), то такое движение тела называется винтовым. Ось Аа называют осью винта. Когда
векторы v и направлены в
одну сторону, то при принятом нами правиле изображения 
винт будет
правым; если в разные стороны, - левым.
Расстояние, проходимое за время одного оборота любой
точкой тела, лежащей на оси винта, называется шагом h винта.
Если величины v и постоянны, то
шаг винта также будет постоянным. Обозначая время одного оборота через Т, получаем в
этом случае 
и 
, откуда h=2πv/ω.
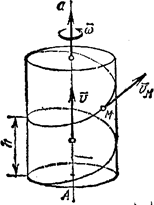
Рис.16
При постоянном шаге любая точка М тела, не лежащая на оси винта, описывает винтовую линию. Скорость
точки М, находящейся от оси винта на
расстоянии 
, слагается из поступательной скорости 
и перпендикулярной ей
скорости, получаемой во вращательном движении, которая численно равна 
. Следовательно,
.
Направлена скорость 
по касательной
к винтовой линии. Если цилиндрическую поверхность, по которой движется точка М, разрезать вдоль образующей и
развернуть, то винтовые линии, обратятся в прямые,
наклоненные к основанию цилиндра под углом 
.
Методические
рекомендации по решению задач
Рассматривается а) сложное движение одного тела, б)
относительное движение нескольких тел.
Требуется установить соотношения между скоростями
(линейными и угловыми), а также ускорениями (линейными и угловыми), при сложном
или относительном движении тел.
Можно
предложить следующий алгоритм решения:
1) Изобразить (или
при наличии некоторого опыта представить) тело или систему тел в двух
состояниях.
2) Из рисунка найти связь между перемещениями -
линейными и угловыми.
3) Продифференцировать полученное соотношение по
времени и учесть определения скорости и ускорения (линейных
и угловых).
Пример 6. На клин с углом наклона α положен брусок. Под действием силы тяжести брусок
опускается со скоростью vб. Найти скорость клина.
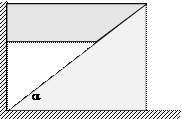
Рис.17
Решение. 1) Под
действием силы тяжести брусок движется вниз, вытесняя клин и заставляя его
перемещаться вправо. Изобразим систему тел в двух состояниях (рис.18).
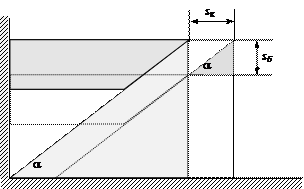
Рис.18
2) Обозначим перемещение клина sк, а
перемещение бруска sб. Из
рисунка легко найти связь между ними:
3) Продифференцируем полученное соотношение по времени
и учтем определение скорости
В результате получим уравнения кинематической связи
Пример
7. На горизонтальной плоскости находится катушка, на которую намотана нить
(рис.19). Радиус намотанного слоя ниток равен r, наибольший радиус катушки равен R. Свободный конец нити перемещают с
ускорением aK. Найти
ускорение центра масс катушки aC и угловое
ускорение ε, если катушка движется без
проскальзывания.
Рис.19
Решение. Решим задачу в
соответствии с приведенным алгоритмом.
1. Изобразим катушку
в двух состояниях.
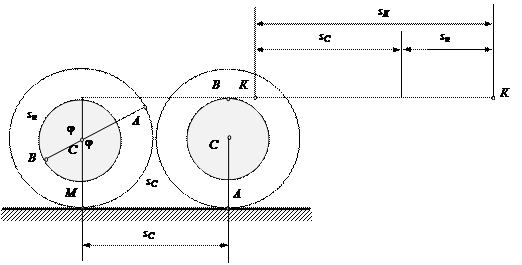
Рис.20
2. Из рисунка найдем связь между перемещениями. Пусть
центр масс С
переместился на расстояние sC. При этом точка А заняла нижнее положение, а
радиус, соединяющий точки А и С повернулся на угол φ. При отсутствии проскальзывания длина дуги АМ равна перемещению центра масс.
Учитывая связь между длиной дуги и углом φ,
опирающимся на эту дугу, получаем
Найдем перемещение конца нити К. При повороте катушки на угол φ точка В заняла
верхнее положение, в результате чего свободная часть нити увеличилась на длину
дуги sн = φ∙r. Следовательно, перемещение конца нити происходит,
во-первых, за счет перемещения самой катушки, во-вторых, за счет увеличения
свободного участка нити:
3. Дважды продифференцируем полученные соотношения по
времени:
и учтем определения ускорения
В результате получим уравнения кинематической связи в
виде
Из этих соотношений выразим искомые величины через
данные условия задачи:
Пример
8. В кулисном механизме при качании
кривошипа ОС вокруг оси О, ползун А,
перемещаясь вдоль кривошипа ОС, приводит в движение стержень АВ, движущийся в вертикальных
направляющих К (рис.21). Расстояние OK=l.
Определить скорость движения ползуна А относительно кривошипа ОС в
функции от его угловой скорости со и угла поворота φ.
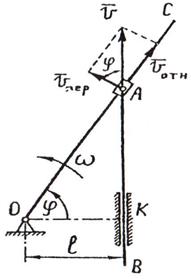
Рис.21
Решение.
Рассмотрим движение точки (ползуна
А). Абсолютным движением этой точки является прямолинейное движение по вертикали.
Движение точки А вдоль
кривошипа ОС, считая кривошип неподвижным, является относительным.
Движение точки А вместе с кривошипом во вращательном
движении вокруг оси О является
переносным.
Абсолютная
скорость точки А
Причем
Пример
9. Кривошип OA и кулиса 01В вращаются вокруг горизонтальных осей О и
O1 (рис.22,а).
Ползун А шарнирно скреплен с кривошипом OA и скользит в прорези кулисы О1В. Угловая
скорость кривошипа ωOA = 4 c-1. Определить угловую скорость кулисы в указанном
положении, если OA =
а)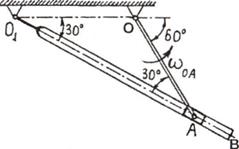
б)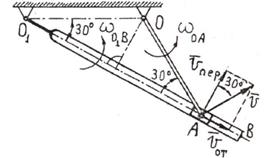
Рис.22
Решение. Абсолютное движение точки А - движение по окружности с
центром в точке О. Разложим это движение на два движения.
Движение точки А
ползуна кривошипа вдоль прорези кулисы, считая кулису неподвижной, является
относительным.
Движение точки А
ползуна кривошипа вместе с кулисой представляет собой переносное движение (как
будто ползун А жестко связан с
кулисой).
Абсолютная скорость точки А (рис.22,б)
Найдем абсолютную и переносную скорости
точки А:
Угловая скорость кулисы
Относительная скорость точки А
Пример
10. Вдоль прорези диска радиусом R = 10 см
движется ползун М, расстояние
которого от центра диска изменяется по закону ОМ = х = (10t - 3t2) см. Диск вращается с постоянной угловой скоростью w = 2 с-1.
Определить абсолютную скорость и абсолютное ускорение ползуна при t1 = 4 с.
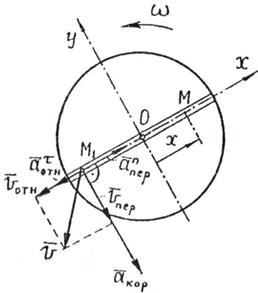
Рис.23
Решение. Движение точки (ползуна M) по прорези диска, считая диск неподвижным, является
относительным. Движение точки М вместе с диском во вращательном
движении является переносным.
Находим положение точки М на диске при t1 = 4 с, ОМ1 =х1
= х(t1) = 10t1 -3t12 = -8 см. Определяем абсолютную скорость точки М
Найдем абсолютное
ускорение точки М
Ускорение
Кориолиса
Построим систему координат Оху . Вычислим проекции абсолютного ускорения точки М на эти оси координат в заданный момент
времени t1
Абсолютное
ускорение точки М
Пример 11. Точка
М движется по ободу диска радиусом R=20 см
согласно закону s = АМ = 6tsin(πt/3). Диск вращается вокруг неподвижной оси О1О2, лежащей в
плоскости диска, в направлении, указанном стрелкой, с постоянной угловой
скоростью ω=0,5 рад/с. Определить абсолютную скорость точки М в момент времени t1=5 с
(рис.24).
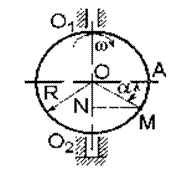
Рис.24
Решение. В
данной задаче относительное движение точки –
движение по ободу диска относительной системы отсчета, связанной с диском;
переносное движение – вращение вместе с
диском вокруг неподвижной оси; абсолютное движение – движение точки относительно неподвижной оси.
Определим
параметры относительного движения точки:
а) положение точки
М в заданный момент времени t=5 с:
Знак минус
означает, что точка М в
рассматриваемый момент времени находится в области отрицательных значений
дуговой координаты s;
б) определим
центральный угол α и отрезок MN:
в) найдем проекцию
относительной скорости vотн точки М на
касательную в данный момент времени (рис. 25).
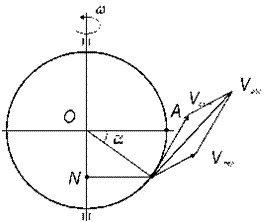
Рис.25
Определим модуль
переносной скорости точки М как
вращательной скорости той точки диска, где в данное мгновение находится точка М
Вектор переносной
скорости перпендикулярен плоскости диска и направлен в сторону его вращения.
Модуль абсолютной
скорости точки М (рис. 25) найдем по
формуле:
Вектор
абсолютной скорости направлен по диагонали прямоугольника, построенного на
относительной и переносной скоростях как сторонах.
Абсолютное
ускорение точки
М равно (рис. 26) геометрической
сумме относительного 
, переносного 
и кориолисова 
ускорений:
, или с учетом условий задачи в развернутом виде
где при t1=5 с касательное ускорение в относительном движении:
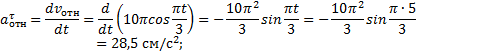
нормальное ускорение в относительном движении:
нормальное
ускорение в переносном движении:
кориолисово ускорение:
Положительный знак
показывает,
что вектор 
направлен
в сторону положительных значений S; вектор 
направлен по
нормали к траектории движения точки в относительном движении, т.е. по нормали к
окружности радиусом MN к её центру, вектор направлен
согласно правилу векторного произведения векторов 
и 
(рис. 26).
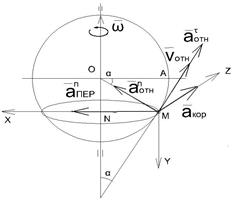
Рис.26
Модуль абсолютного
ускорения точки М находим способом
проекции на оси х, у и
z (рис. 26):
Направление
вектора 
определяется
его углами с осями координат:
Пример 12. Кривошип ОА длиной R=64 см вращается вокруг
неподвижной оси О
с постоянной угловой скоростью ω=1 рад/с и приводит в движение
шатун АВ длиной L=72 см и ползун В. Для положения механизма, заданного значениями углов α=45°, β=30° найти скорость
и ускорение ползуна В. Схема механизма приведена на рис. 27.
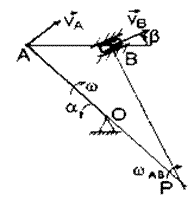
Рис.27
Решение. 1. Определим скорость точки А
как вращательную вокруг неподвижной точки О
по соотношению 
Для определения
скорости точки В найдем положение
мгновенного центра скоростей Р,
для чего покажем направление скоростей точек А и В, а затем из точек А и В восстановим перпендикуляры к их
скоростям vA и vB. Точка пересечения перпендикуляров будет являться
мгновенным центром скоростей Р (см. рис. 27).
Рассмотрим
движение шатуна в данный момент времени как вращательное относительно оси,
проходящей через мгновенный центр скоростей Р перпендикулярно неподвижной плоскости, по отношению к которой
происходит плоское движение. Угловая скорость шатуна в этом случае определяется из соотношения 
, а скорость ползуна В как вращательная – из
соотношения 
.
Расстояния АР и BP определим
из решения треугольника АВР, применив
теорему синусов. Для заданного положения механизма получим
откуда
Подставив
найденные значения расстояний в соответствующие формулы, получим
Направления
скоростей показаны на рис.27.
2. Для определения
ускорения ползуна B воспользуемся векторным равенством:
где 
–
ускорение ползуна В;
–
ускорение точки А,
выбранной за полюс;
–
осестремительное (нормальное) ускорение точки В при ее вращении
вокруг полюса А;
–
вращательное (касательное) ускорение точки В при ее вращении вокруг полюса
А.
Ускорение точки А кривошипа при равномерном вращении
вокруг неподвижной оси О состоит
только из осестремительной составляющей, модуль
которой определяется формулой
Вектор ускорения
точки А направлен к оси вращения (рис.28),
Осестремительное ускорение
точки В при
ее вращении вокруг полюса А:
Рис.28
Рассчитать
вращательное ускорение обычным
способом не представляется возможным, так как величина углового ускорения звена
АВ неизвестна. Несмотря на это
обстоятельство, векторное равенство (1) позволяет найти
ускорение ползуна В. Для этого
воспользуемся тем, что нам известно направления вектора (он
перпендикулярен ускорению ) и вектора ускорения искомого ускорения (вдоль
прямолинейной траектории точки В).
Проведем вектор
ускорения точки В, предполагая, что он направлен противоположно скорости
точки В. Спроектируем векторное
равенство (1) на ось u,
перпендикулярную ускорению и проходящую
через точки А и В, получим
Отсюда
Знак минус
показывает, что истинное направление ускорения точки В противоположно принятому.
Вопросы для самопроверки
- Приведите определение абсолютного (сложного)
движения точки.
- Абсолютное, относительное, переносное движение
точки.
- Какое движение твердого тела называют простым?
- Какие системы координат выбирают при определении
скоростей твердых тел при сложном движении?
- Какое движение считают переносным, а какое –
относительным?
- Какое движение точки
называется относительным и какое переносным?
- Сформулируйте теорему о сложении скоростей для точки, совершающей сложное движение..
- В чем состоит различие между абсолютной и
относительной производными векторной функции скалярного аргумента?
- Что выражает формула Бура?
- Как выражается вектор абсолютной скорости точки в
общем случае ее движения?
- Точка совершает сложное движение. Переносное движение - вращение вокруг оси. Как определить переносную скорость точки?
- Точка совершает сложное движение. Переносное движение - поступательное. Как определить переносную скорость точки?
- Точка совершает сложное движение. Переносное движение - вращение вокруг оси. Как определить переносное ускорение точки?
- Как должна двигаться вспомогательная система отсчета, чтобы переносное ускорение точки (при сложном ее движении) было равно нулю?
- Назовите составляющие вектора ускорения при сложном
движении точки.
- Дайте определение ускорения Кориолиса. Как определяются модуль и направление ускорения
Кориолиса?
- При каком сложном движении точки ускорение Кориолиса
равно нулю?
- Каким должно быть относительное движение точки для того, чтобы ее относительное ускорение было равно нулю?
- Дайте определение относительного, переносного и
абсолютного движений точки, а также скоростей и ускорений этих движений.
- Как определяют абсолютную скорость точки в сложном
движении?
- Как определяют абсолютное ускорение точки при
непоступательном переносном движении и при поступательном переносном движении?
- По образующей цилиндра, равномерно вращающегося вокруг своей оси, равномерно движется точка. Чему равно и как направлено ее абсолютное ускорение?
- Чему равна проекция ускорения Кориолиса движущейся точки на направление ее относительной скорости?
- Каковы причины появления кориолисова
ускорения?
- Может ли абсолютное ускорение точки состоять из одного переносного ускорения?
- Может ли абсолютное ускорение точки состоять из одного относительного ускорения?
- Может ли абсолютное ускорение точки состоять из одного ускорения Кориолиса?
- Почему ускорение Кориолиса точек при плоском движении тела равно нулю?
- Каковы модуль и направление кориолисова
ускорения и при каких
условиях кориолисово ускорение точки равно нулю?
- Какой вид имеет выражение абсолютного ускорения
точки в случае, когда переносное движение представляет собой свободное движение
твердого тела, и в случае, когда переносное движение является вращением вокруг
неподвижной оси?
- Теорема о сложении ускорений точки в том случае,
когда переносное движение является произвольным.
- Назвать случаи, когда кориолисово
ускорение точки равно нулю.
- Сформулируйте определения абсолютного,
относительного и переносного движений твердого тела.
- Как определить скорость произвольной точки тела,
совершающего поступательное переносное и поступательное относительное движения?
- Что собой представляет результирующее движение при
вращении тела одновременно в одну и ту же сторону вокруг параллельных осей?
- Что называется парой вращений? Чему эквивалентна
пара вращений?
- Чему равна мгновенная угловая скорость тела,
совершающего вращения вокруг пересекающихся осей?
- Какое движение тела называется винтовым? Сложением каких движений оно получается?
- Что представляет собой абсолютное движение тела,
участвующего в нескольких вращениях вокруг сходящихся мгновенных осей?
- Как по уравнениям сферического движения твердого
тела определяют его угловую скорость?
- Каковы проекции углового ускорения тела при
сферическом движении на неподвижные и подвижные координатные оси?
- Чему равно абсолютное угловое ускорение твердого
тела, вращающегося неравномерно вокруг двух пересекающихся осей?
- Какое угловое ускорение твердого тела называют
поворотным и чему оно равно?
- Что характеризует поворотное угловое ускорение?
- Как определяют угловую скорость твердого тела,
вращающегося вокруг двух параллельных осей в одну и разные стороны?
- Появляется ли поворотное угловое ускорение при
неравномерном вращении твердого тела вокруг параллельных осей?
- Что называют парой угловых скоростей и при каком
условии пара угловых скоростей эквивалентна поступательному движению? Чему
равна скорость этого поступательного движения?
- Какие понятия из статики аналогичны угловой скорости
вращения тела и скорости поступательного движения тела?
- Что представляет собой абсолютное движение тела, участвующего в нескольких вращениях вокруг сходящихся мгновенных осей?
- Как определяют угловую скорость твердого тела, вращающегося вокруг двух параллельных осей в одну и разные стороны?
- Как формулируется теорема о сложении вращений вокруг параллельных осей? Вокруг персекающихся осей?
- Что представляет собой движение твердого тела, участвующего в нескольких вращениях вокруг произвольных осей и в нескольких поступательных движениях?
- Что такое мгновенная ось вращения, мгновенная угловая скорость, мгновенное угловое ускорение?
- Что такое переносное движение точки?
1) движение точки совершаемое относительно подвижной системы отсчета;
2) движение, совершаемое подвижной системой отсчета (и связанными с ней точками) относительно неподвижной системы отсчета;
3) движение точки, совершаемое по отношению к неподвижной системе отсчета.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
