Главная

Лекция 4. Центр тяжести.

В данной лекции рассматриваются следующие вопросы

1. Центр тяжести твердого тела.

2. Координаты центров тяжести неоднородных тел.

3. Координаты центров тяжести однородных тел.

4. Способы определения координат центров тяжести.

5. Центры тяжести некоторых однородных тел.

Изучение данных вопросов необходимо в дальнейшем для изучения динамики движении тел с учетом трения скольжения и трения качения, динамики движения центра масс механической системы, кинетических моментов, для решения задач в дисциплине «Сопротивление материалов».

Приведение параллельных сил.

После того как было рассмотрено приведение к центру плоской системы и произвольной пространственной системы сил, мы опять возвращаемся к рассмотрению частного случая системы параллельных сил.

Приведение двух параллельных сил.

В ходе рассмотрения такой системы сил возможны три следующих случая приведения.

1. Система двух коллинеарных сил. Рассмотрим систему двух параллельных и направленных в одну сторону сил P и Q, приложенных в точках А и В. Будем считать, что силы перпендикулярны к этому отрезку (рис.1,а).

Выберем в качестве центра приведения точку С, принадлежащую отрезку АВ и удовлетворяющую условию:

АС/СВ = Q/P. (1)

Главный вектор системы R_C = P + Q по модулю равен сумме этих сил: R_C = P + Q.

Главный момент относительно центра С с учетом (1) равен нулю: M_C = P∙АС - Q∙СВ = 0.

Таким образом, в результате приведения мы получили: R_C ≠ 0, M_C = 0. Это означает, что главный вектор эквивалентен равнодействующей, проходящей через центр приведения, то есть:

Равнодействующая коллинеарных сил равна по модулю их сумме, а ее линия действия делит отрезок, соединяющий точки их приложения, обратно пропорционально модулям этих сил внутренним образом.

Отметим, что положение точки С не изменится, если силы Р и Q повернуть на угол α. Точка С, обладающая таким свойством называется центром параллельных сил.

2. Система двух антиколлинеарных и не равных по модулю сил. Пусть силы P и Q , приложенные в точках А и В, параллельны, направлены в противоположные стороны и по модулю не равны (рис.1,б).

Выберем в качестве центра приведения точку С, удовлетворяющую по-прежнему соотношению (1) и лежащую на той же прямой, но за пределами отрезка АВ.

Главный вектор этой системы R_C = P + Q по модулю теперь будет равен разности модулей векторов: R_C = Q - P.

Главный момент относительно центра С по-прежнему равен нулю: M_C = P∙АС - Q∙СВ = 0, поэтому

Равнодействующая антиколлинеарных и не равных по модулю сил равна их разности, направлена в сторону большей силы, а ее линия действия делит отрезок, соединяющий точки их приложения, обратно пропорционально модулям этих сил внешним образом.

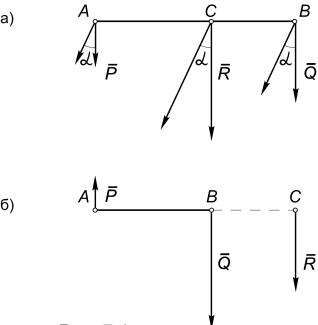
Рис.1

3. Система двух антиколлинеарных и равных по модулю сил. Возьмем за исходный предыдущий случай приведения. Зафиксируем силу Р, а силу Q устремим по модулю к силе Р.

Тогда при Q → Р в формуле (1) отношение АС/СВ → 1. Это означает, что АС → СВ , то есть расстояние АС →∞.

При этом модуль главного вектора R_C → 0, а модуль главного момента не зависит от положения центра приведения и остается равным первоначальному значению:

M_C = P∙АС - Q∙СВ = P∙(АС - СВ) = P∙АB.

Итак, в пределе мы получили систему сил, для которой R_C = 0, M_C ≠0, а центр приведения удален в бесконечность, которую нельзя заменить равнодействующей. В этой системе нетрудно узнать пару сил, поэтому пара сил равнодействующей не имеет.

Центр системы параллельных сил.

Рассмотрим систему n сил P_i, приложенных в точках A_i (x_i, y_i, z_i) и параллельных оси Ov c ортом l (рис.2).

Если заранее исключить случай системы, эквивалентной паре сил, нетрудно на основании предыдущего параграфа доказать существование ее равнодействующей R.

Определим координаты центра C(x_c, y_c, z_c) параллельных сил, то есть координаты точки приложения равнодействующей этой системы.

Воспользуемся с этой целью теоремой Вариньона, на основании которой:

M₀ (R) = ΣM₀ (P_i).

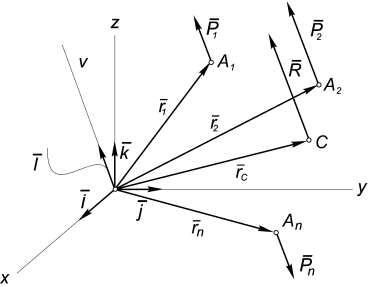
Рис.2

Вектор-момент силы можно представить в виде векторного произведения, поэтому:

М₀(R) = r_c×R = ΣМ_0i (P_i) = Σ(r_i×P_i).

Учитывая, что R = R_v∙l, а P_i = P_vi∙l и воспользовавшись свойствами векторного произведения, получим:

r_c×R_v∙l = Σ(r_i ×P_vi∙l),

r_c∙R_v×l = Σ(r_i∙P_vi×l) = Σ(r_i∙P_vi)×l,

или:

[r_cR_v - Σ(r_i P_vi )]×l = 0.

Последнее выражение справедливо только в том случае, если выражение в квадратных скобках равно нулю. Поэтому, опуская индекс v и учитывая, что равнодействующая R = ΣP_i , отсюда получим:

r_c = (ΣP_i r_i)/(ΣP_i).

Проектируя последнее векторное равенство на оси координат, получим искомое выражение координат центра параллельных сил:

x_c = (ΣP_i x_i)/( ΣP_i);

y_c = (ΣP_i y_i)/( ΣP_i); (2)

z_c = (ΣP_i z_i)/( ΣP_i).

Центр тяжести тел.

Координаты центров тяжести однородного тела.

Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.

Если разбить тело на элементарные части объемом ∆V_i , то на каждую его часть будет действовать сила притяжения ∆P_i, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.3), и к ней применимы все выводы предыдущей главы.

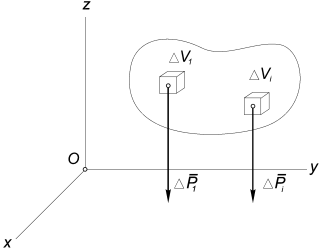
Рис.3

Определение. Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.

Напомним, что удельным весом элементарной части тела называется отношение ее веса ∆P_i к объему ∆V_i: γ_i = ∆P_i/∆V_i. Для однородного тела эта величина является постоянной: γ_i = γ = P/V.

Подставляя в (2) ∆P_i = γ_i ∙∆V_i вместо P_i, учитывая последнее замечание и сокращая числитель и знаменатель на g, получим выражения координат центра тяжести однородного тела:

x_c = (Σ∆V_i∙x_i)/(Σ∆V_i);

y_c = (Σ∆V_i∙y_i)/(Σ∆V_i); (3)

z_c = (Σ∆V_i∙z_i)/(Σ∆V_i).

При определении центра тяжести полезны несколько теорем.

1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой плоскости.

Если оси х и у расположить в этой плоскости симметрии, то для каждой точки с координатами можно отыскать точку с координатами . И координата по (3), будет равна нулю, т.к. в сумме все члены имеющие противоположные знаки, попарно уничтожаются. Значит центр тяжести расположен в плоскости симметрии.

2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Действительно, в этом случае, если ось z провести по оси симметрии, для каждой точки с координатами можно отыскать точку с координатами и координаты и , вычисленные по формулам (3), окажутся равными нулю.

Аналогично доказывается и третья теорема.

3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.

И ещё несколько замечаний.

Первое. Если тело можно разделить на части, у которых известны вес и положение центра тяжести, то незачем рассматривать каждую точку, а в формулах (3) P_i – определять как вес соответствующей части и – как координаты её центра тяжести.

Второе. Если тело однородное, то вес отдельной части его , где - удельный вес материала, из которого сделано тело, а V_i - объём этой части тела. И формулы (3) примут более удобный вид. Например,

И аналогично, где - объём всего тела.

Третье замечание. Пусть тело имеет вид тонкой пластинки площадью F и толщиной t, лежащей в плоскости Oxy. Подставляя в (3) ∆V_i = t∙∆F_i, получим координаты центра тяжести однородной пластинки:

x_c = (Σ∆F_i∙x_i) / (Σ∆F_i);

y_c = (Σ∆F_i∙y_i) / (Σ∆F_i).

z_c = (Σ∆F_i∙z_i) / (Σ∆F_i).

где – координаты центра тяжести отдельных пластин; – общая площадь тела.

Четвёртое замечание. Для тела в виде тонкого криволинейного стержня длиной L с площадью поперечного сечения a элементарный объем ∆V_i = a∙∆L_i, поэтому координаты центра тяжести тонкого криволинейного стержня будут равны:

x_c = (Σ∆L_i∙x_i)/(Σ∆L_i);

y_c = (Σ∆L_i∙y_i)/(Σ∆L_i); (4)

z_c = (Σ∆L_i∙z_i)/(Σ∆L_i).

где – координаты центра тяжести i-го участка; .

Отметим, что согласно определению центр тяжести - это точка геометрическая; она может лежать и вне пределов данного тела (например, для кольца).

Примечание.

В этом разделе курса мы не делаем разницы между силой притяжения, силой тяжести и весом тела. В действительности сила тяжести представляет собой разность между силой притяжения Земли и центробежной силой, вызванной ее вращением.

Координаты центров тяжести неоднородных тел.

Координаты центра тяжести неоднородного твердого тела (рис.4) в выбранной системе отсчета определяются следующим образом:

Рис.4

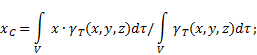
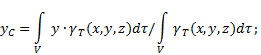
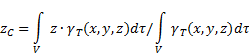
где - вес единицы объема тела (удельный вес)

- вес всего тела.

Если твердое тело представляет собой неоднородную поверхность (рис.5), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

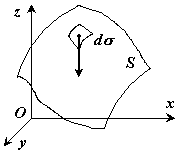
Рис.5

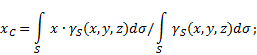
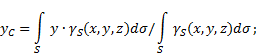
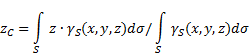
где - вес единицы площади тела,

- вес всего тела.

Если твердое тело представляет собой неоднородную линию (рис.6), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

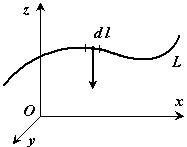
Рис.6

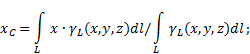
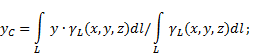
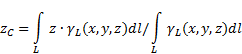
где - вес единицы длины тела,

- вес всего тела.

Способы определения координат центра тяжести.

Исходя из полученных выше общих формул, можно указать конкретные способы определения координат центров тяжести тел.

1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.7), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

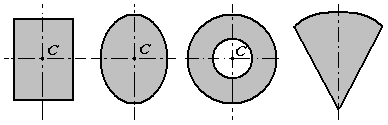
Рис.7

2. Разбиение. Тело разбивается на конечное число частей (рис.8), для каждой из которых положение центра тяжести и площадь известны.

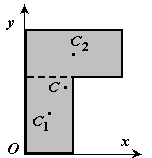
Рис.8

S=S₁+S₂.

3. Метод отрицательных площадей. Частный случай способа разбиения (рис.9). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S₁ и площади вырезанной части S₂ .

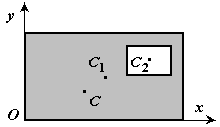
Рис.9

S=S₁-S₂.

4. Метод группировки. Является хорошим дополнением двух последних методов. После разбиения фигуры на составные элементы часть их бывает удобно объединить вновь, чтобы затем упростить решение путем учета симметрии этой группы.

Центры тяжести некоторых однородных тел.

1) Центр тяжести дуги окружности. Рассмотрим дугу АВ радиуса R с центральным углом . В силу симметрии центр тяжести этой дуги лежит на оси Ox (рис. 10).

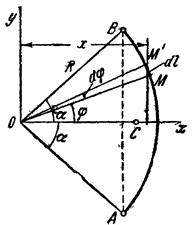
Рис.10

Найдем координату по формуле . Для этого выделим на дуге АВ элемент ММ’ длиною , положение которого определяется углом . Координата х элемента ММ’ будет . Подставляя эти значения х и dl и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:

где L - длина дуги АВ, равная .

Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном

где угол измеряется в радианах.

2) Центр тяжести площади треугольника. Рассмотрим треугольник, лежащий в плоскости Oxy, координаты вершин которого известны: A_i (x_i,y_i), (i = 1,2,3). Разбивая треугольник на узкие полоски, параллельные стороне А₁А₂ , придем к выводу, что центр тяжести треугольника должен принадлежать медиане А₃ М₃ (рис.11)_.

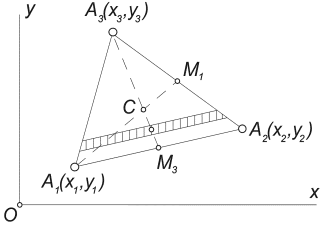
Рис.11

Разбивая треугольник на полоски, параллельные стороне А₂А₃, можно убедиться, что он должен лежать на медиане А₁М₁. Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан, которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.

В частности, для медианы А₁М₁ получим, учитывая, что координаты точки М₁ - это среднее арифметическое координат вершин А₂ и А_{3 :}

x_c = x₁ + (2/3)∙(x_М1 - x₁) = x₁ + (2/3)∙[(x₂ + x₃)/2-x₁] = (x₁+ x₂ +x₃)/3.

Таким образом, координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин:

x_c =(1/3)Σx_i ; y_c =(1/3)Σy_i.

3) Центр тяжести площади кругового сектора. Рассмотрим сектор круга радиуса R с центральным углом 2α, расположенный симметрично относительно оси Ox (рис.12) .

Очевидно, что y_c = 0, а расстояние от центра круга, из которого вырезан этот сектор, до его центра тяжести можно определить по формуле:

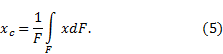
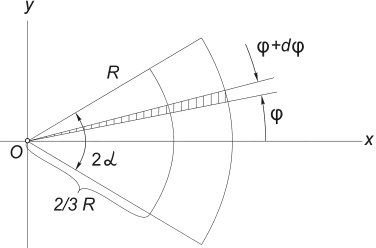
Рис.12

Проще всего этот интеграл вычислить, разбивая область интегрирования на элементарные секторы с углом dφ. С точностью до бесконечно малых первого порядка такой сектор можно заменить треугольником с основанием, равным R×dφ и высотой R. Площадь такого треугольника dF=(1/2)R²∙dφ, а его центр тяжести находится на расстоянии 2/3R от вершины, поэтому в (5) положим x = (2/3)R∙cosφ. Подставляя в (5) F = αR², получим:

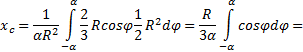
С помощью последней формулы вычислим, в частности, расстояние до центра тяжести полукруга.

Подставляя в (2) α = π/2, получим: x_c = (4R)/(3π) ≅ 0,4R .

Пример 1. Определим центр тяжести однородного тела, изображённого на рис. 13.

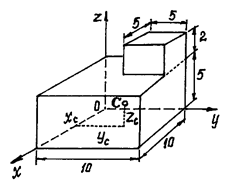
Рис.13

Решение. Тело однородное, состоящее из двух частей, имеющих симметричную форму. Координаты центров тяжести их:

Объёмы их:

Поэтому координаты центра тяжести тела

Пример 2. Найдем центр тяжести пластины, согнутой под прямым углом. Размеры – на чертеже (рис.14).

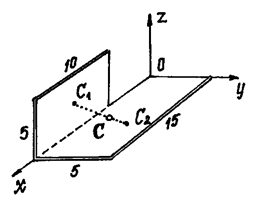
Рис.14

Решение. Координаты центров тяжести:

0.

Площади:

Поэтому:

Рис. 6.5.

Пример 3. У квадратного листа см вырезано квадратное отверстие см (рис.15). Найдем центр тяжести листа.

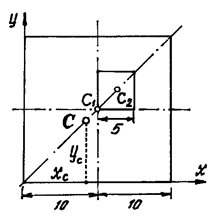
Рис.15

Решение. В этой задаче удобнее разделить тело на две части: большой квадрат и квадратное отверстие. Только площадь отверстия надо считать отрицательной. Тогда координаты центра тяжести листа с отверстием:

координата так как тело имеет ось симметрии (диагональ).

Пример 4. Найти положение центра тяжести пластинки, представленной на рис. 16. Размеры даны в сантиметрах.

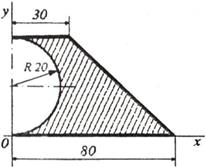
Рис.16

Решение. Разделим пластинку на фигуры (рис. 17), центры тяжести которых известны.

Площади этих фигур и координаты их центров тяжести:

1) прямоугольник со сторонами 30 и 40 см, S₁ =30∙40=1200 см²; х₁=15 см; у₁ =20 см.

2) прямоугольный треугольник с основанием 50 см и высотой 40 см; S₂ =0,5∙50∙40= 1000 см²; х₂=30+50/3=46,7 см; у₂=40/3=13,3 см;

3) половина круга окружности радиуса r=20 см; S₃ =0,5∙π∙20² =628 см²; х₃ =4R/3π=8,5 см; у₃ =20 см.

Координаты центра тяжести пластинки определяются по формулам (площадь половины круга считаем отрицательной)

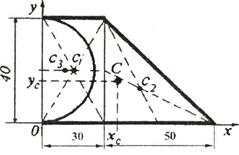
Рис.17

где s — площадь всей пластины; s_k - площади ее частей.

Пример 5. Проволочная скобка (рис.18) состоит из трёх участков одинаковой длины l.

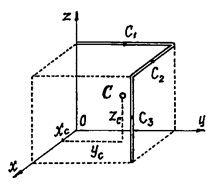
Рис.18

Решение. Координаты центров тяжести участков:

Поэтому координаты центра тяжести всей скобки:

Пример 6. Определить положение центра тяжести фермы, все стержни которой имеют одинаковую погонную плотность (рис.19).

Решение. Напомним, что в физике плотность тела ρ и его удельный вес g связаны соотношением: γ= ρg , где g - ускорение свободного падения. Чтобы найти массу такого однородного тела, нужно плотность умножить на его объем.

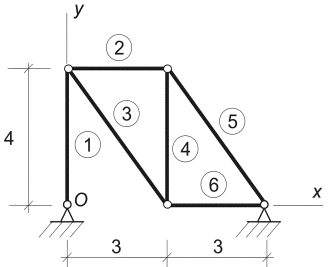
Рис.19

Термин «линейная» или «погонная» плотность означает, что для определения массы стержня фермы нужно погонную плотность умножить на длину этого стержня.

Для решения задачи можно воспользоваться методом разбиения. Представив заданную ферму в виде суммы 6 отдельных стержней, получим:

где L_i длина i-го стержня фермы, а x_i, y_i - координаты его центра тяжести.

Решение этой задачи можно упростить, если сгруппировать 5 последних стержней фермы. Нетрудно видеть, что они образуют фигуру, имеющую центр симметрии, расположенный посредине четвертого стержня, где и находится центр тяжести этой группы стержней.

Таким образом, заданную ферму можно представить комбинацией всего двух групп стержней.

Первая группа состоит из первого стержня, для нее L₁ = 4 м, x₁ = 0 м, y₁= 2 м. Вторая группа стержней состоит из пяти стержней, для нее L₂ = 20 м, x₂= 3 м, y₂= 2 м.

Координаты центра тяжести фермы находим по формуле:

x_c = (L₁∙x₁ + L₂∙x₂)/(L₁+ L₂) = (4∙0 + 20∙3)/24 = 5/2 м;

y_c = (L₁∙y₁ + L₂∙y₂)/(L₁+ L₂) = (4∙2 + 20∙2)/24 = 2 м.

Отметим, что центр С лежит на прямой, соединяющей С₁ и С₂ и делит отрезок С₁С₂ в отношении: С₁С/СС₂ = (x_c - x₁)/(x₂ - x_c) = L₂ / L₁ = 2,5/0,5.

Вопросы для самопроверки

- Что называется центром параллельных сил?

- Как определяются координаты центра параллельных сил?

- Как определить центр параллельных сил, равнодействующая которых равна нулю?

- Каким свойством обладает центр параллельных сил?

- По каким формулам вычисляются координаты центра параллельных сил?

- Что называется центром тяжести тела?

- Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?

- Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?

- Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга?

- Что называют статическим моментом площади?

- Приведите пример тела, центр тяжести которого расположен вне тела.

- Как используются свойства симметрии при определении центров тяжести тел?

- В чем состоит сущность способа отрицательных весов?

- Где расположен центр тяжести дуги окружности?

- Каким графическим построением можно найти центр тяжести треугольника?

- Запишите формулу, определяющую центр тяжести кругового сектора.

- Используя формулы, определяющие центры тяжести треугольника и кругового сектора, выведите аналогичную формулу для кругового сегмента.

- По каким формулам вычисляются координаты центров тяжести однородных тел, плоских фигур и линий?

- Что называется статическим моментом площади плоской фигуры относительно оси, как он вычисляется и какую размерность имеет?

- Как определить положение центра тяжести площади, если известно положение центров тяжести отдельных ее частей?

- Какими вспомогательными теоремами пользуются при определении положения центра тяжести?

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00