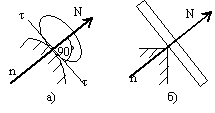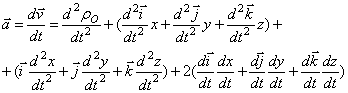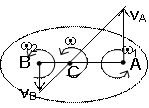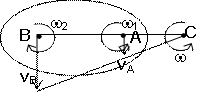Главная
Глоссарий
А
аксиома
присоединения и исключения уравновешивающихся сил
аксиома
равенства действия и противодействия
Б
В
векторный
способ задания движения
возможные
(виртуальные) перемещения
вынужденные
колебания при наличии вязкого трения
Г
главная
центральная ось инерции
главный
момент количеств движения системы
Д
движение
свободного твердого тела
дифференциальные
уравнения движения центра масс
дифференциальные
уравнения движения системы точек
дифференциальные
уравнения плоского движения твердого тела
дифференциальные
уравнения поступательного движения тела
дифференциальные
уравнения вращения тела вокруг неподвижной оси
Е
естественный
способ задания движения
З
закон
Кулона (Амонтона – Кулона)
закон
равенства действия и противодействия
закон
сохранения движения центра масс
закон
сохранения кинетического момента
закон
сохранения количества движения
закон
сохранения полной механической энергии
И
К
кинематические
уравнения Эйлера
кинетическая
энергия материальной точки
колебательное
движение материальной точки
количество
движения материальной точки
координатный
способ задания движения
коэффициент
полезного действия
Л
лемма
о параллельном переносе силы
М
мгновенный
центр вращений (ось вращений)
модуль
силы (для плоской системы)
модуль
силы (для пространственной системы)
момент
инерции материальной точки
момент
количества движения материальной точки
момент
силы относительно точки
Н
направляющие
косинусы (для плоской системы)
направляющие
косинусы (для пространственной системы)
О
П
план
решения задач на равновесие сил
плоское
(плоскопараллельное) движение
потенциальная
энергия восстанавливающей силы пружин
правило
параллелограмма угловых скоростей
приведение
пространственной системы сил
приведенная
длина физического маятника
проекция
силы на ось координат (для плоской системы)
проекция
силы на ось координат (для пространственной системы)
Р
равнодействующая
плоской системы сходящихся сил
равнодействующая
пространственной системы сходящихся сил
равномерное
прямолинейное движение
равнопеременное
криволинейное движение
равноускоренное
(равнозамедленное) движение
разложение
силы на составляющие (для плоской системы)
разложение
силы на составляющие (для пространственной системы)
С
сложение
вращений вокруг 2-х параллельных осей
сложение
поступательного и вращательного движений
сложное
движение твердого тела
статический
момент площади плоской фигуры
сферическое
движение твердого тела
Т
теорема
о движении центра масс системы
теорема
о моменте равнодействующей силы
теорема
о параллельном переносе силы
теорема
о проекциях скоростей двух точек тела
теорема
о трех непараллельных силах
теорема
об изменении кинетического момента
теорема
об изменении кинетической энергии материальной точки
теорема
об изменении кинетической энергии системы
теорема
об изменении количества движения материальной точки
теорема
об изменении количества движения системы
теорема
об изменении момента количеств движения системы
теорема
об изменении момента количества движения точки
теорема
Пуансо (о качении центроид)
теорема
Эйлера-Даламбера (о теле, с одной неподвижной точкой)
У
условия
равновесия плоской системы сил
условия
равновесия пространственной системы сил
условия
равновесия сил приложенных к рычагу
условия
равновесия системы параллельных сил
условия
равновесия системы сходящихся сил
Ф
Ц
центр
качаний физического маятника.
Ч
Ш
Э
Статика
Статика. Аксиомы
статики. Система сходящихся сил. Теория пар сил.
Теоретическая механика - естественная наука, изуч. законы
движения и условия равновесия материальных тел под действием приложенных к ним
сил.
Статика – раздел теоретической
механики, в котором рассматриваются задачи на равновесие систем сил.
Равновесие – это состояние, при котором тело при действии сил остается неподвижным
или движется равномерно прямолинейно.
Механическое движение - это изменение с течением времени взаимного
положения в пространстве материальных тел.
Механическое взаимодействие - тот вид взаимодействия между материальными
телами, в результате, которого изменяется состояние движения тел или их форма
(т.е. они деформируют).
Тело (абсолютно твердое
тело, твердое тело) –
материальное тело, расстояние между любыми точками в котором не изменяется.
Следствие размеры и форма тела не изменяются.
Материальная точка – тело,
размерами которого по условиям задачи можно пренебречь.
Механическая система –
совокупность взаимосвязанных между собой тел или материальных точек. Твердое
тело можно рассматривать как механическую систему, положения и расстояние между
точками которой не изменяются.
Сила – мера механического
взаимодействия тел. Сила векторная величина, характеризуется тремя элементами:
числовым значением (модулем), направлением и точкой приложения. Единица
измерения – ньютон, 1Н = 1кгм/с2, 1кН (килоньютон)= 103Н.
Линия действия силы - прямая,
по которой направлена сила.
Эквивалентные сист. сил - 2
сист. сил при замене действия на тело одной сист.сил
другой сист. сил в состоянии движения тела при такой замене не изменится.
Равнодействующая сила - сила при которой одна сила заменяет действие на тело сист.
сил.
Уравновешивающая сила - сила
равная по модулю равнодействующей действующей по одной прямой и направлена в
противоположную сторону.
Сосредоточенная сила - сила,
приложенная в одной точке тела.
Распределённые силы (распределенная нагрузка) – силы, приложенные ко всем частицам объёмного тела или части его поверхности. Распределенная нагрузка задается силой, действующей на единицу объема (поверхности, длины). Размерность распределенной нагрузки – Н/м3 (Н/м2, Н/м).
Аксиомы
(законы) статики:
1)
аксиома инерции: Под действием взаимно уравновешивающихся сил
материальная точка (тело) находится в состоянии покоя или движется прямолинейно
и равномерно.
2)
аксиома равновесия двух сил: Две силы, приложенные к абсолютно твердому телу,
будут уравновешены тогда и только тогда, когда они равны по модулю, действуют
по одной прямой и направлены в противоположные стороны.
3)
аксиома присоединения и
исключения уравновешивающихся сил:
Действие системы сил на абсолютно твердое тело не изменится, если к ней
прибавить или отнять уравновешенную систему сил. Следствие: Действие силы на
абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль
ее линии действия. Т.е. сила, приложенная к абсолютно твердому телу – скользящий вектор.
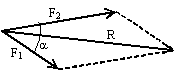
4)
аксиома параллелограмма сил: Равнодействующая двух пересекающихся сил приложена
в точке их пересечения и изображается диагональю параллелограмма, построенного
на этих силах. 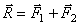 ;
; 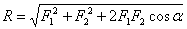 .
.
5)
аксиома равенства действия и
противодействия (3-й закон Ньютона):
Всякому действию соответствует равное и противоположно направленное
противодействие.
6)
принцип отвердевания: Равновесие сил, приложенных к нетвердому телу, не
нарушается при его затвердевании.
Свободным называется тело, если
его перемещения ничем не ограничены.
Несвободным называется тело,
перемещение которого ограничено другими телами.
Связями называются тела,
ограничивающие перемещения данного тела.
Реакции связей – это силы, с
которыми связи действуют на данное тело.
Принцип освобождаемости: Всякое
несвободное тело можно рассматривать как свободное, если действие связей
заменить их реакциями, приложенными к телу.
Реакции опоры - сила, которая
полностью заменяет действие связи или опоры на тело.
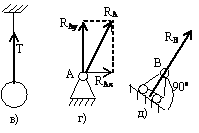
Основные типы связей: а) опора на идеально гладкую поверхность – реакция
поверхности направлена по нормали к ней, т.е. перпендикулярно касательной – нормальная реакция; б) одна из соприкасающихся поверхностей является
точкой (угол), реакция направлена по нормали к другой поверхности; в) нить –
реакция направлена вдоль нити к точке подвеса; г) цилиндрический шарнир
(шарнирно-неподвижная опора) – реакция может иметь любое направление в
плоскости. При решении задач
заменяется двумя взаимно перпендикулярными составляющими; д) цилиндрическая
шарнирно-подвижная опора (шарнир на катках) – реакция направлена перпендикулярно
опорной плоскости; е) сферический (шаровой) шарнир – реакция может иметь любое
направление в пространстве. При решении задач заменяется тремя взаимно
перпендикулярными составляющими; ж) невесомый стержень (обязательно невесомый)
– реакция направлена вдоль стержня; з) "глухая" заделка (вмурованная
балка) – возникает произвольно направленная реакция – сила и реактивный момент,
также неизвестный по направлению. Реакция раскладывается на две составляющие.
Система сходящихся сил.
Сходящимися называются силы, линии действия которых
пересекаются в одной точке.
Произвольная система сил –
система сил, линии действия которых не пересекаются в
одной точке.
Уравновешенная система сил –
система сил, которая будучи приложена к свободному
твердому телу не изменяет его механического состояния (не выводит из
равновесия):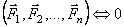
Равнодействующая сходящихся сил равна геометрической сумме этих сил и приложена в
точке их пересечения 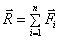 . Равнодействующая может быть найдена геометрическим способом
– построением силового (векторного) многоугольника или аналитическим способом,
проектируя силы на оси координат. Равнодействующая направлена по прямой,
соединяющей начало первой и конец последней силы.
. Равнодействующая может быть найдена геометрическим способом
– построением силового (векторного) многоугольника или аналитическим способом,
проектируя силы на оси координат. Равнодействующая направлена по прямой,
соединяющей начало первой и конец последней силы.
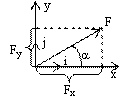
Проекции силы на оси координат (для плоской системы): 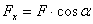 ;
; 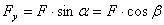 ; проекция
>0, если направление составляющей силы совпадает с направлением оси,
проекция =0, если направление составляющей силы перпендикулярно направлению
оси.
; проекция
>0, если направление составляющей силы совпадает с направлением оси,
проекция =0, если направление составляющей силы перпендикулярно направлению
оси.
Модуль силы (для плоской системы): 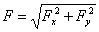 ;
;
Направляющие косинусы (для плоской системы): 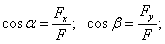
Разложение силы на составляющие
(для плоской системы): 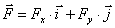 , где
, где 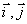 – орт (единичный вектор)
соответствующей оси.
– орт (единичный вектор)
соответствующей оси.
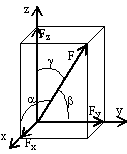
Проекции силы на оси координат (для пространственной системы): 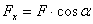 ;
; 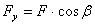 ;
; 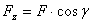 .
.
Разложение силы на составляющие (для пространственной системы): 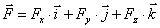 .
.
Модуль силы (для пространственной системы): 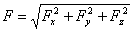 .
.
Направляющие косинусы (для пространственной системы): 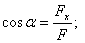
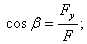
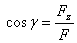 .
.
Проекции равнодействующей системы сходящихся
сил на координатные оси равна алгебраическим суммам проекций этих сил на
соответствующие оси: 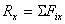 ;
; 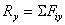 ;
; 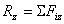 ;
; 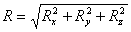 .
.
Условия равновесия системы сходящихся сил: геометрическое: 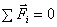 , аналитические:
, аналитические: 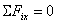 ;
; 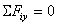 ;
; 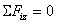 . Условиями равновесия
выражаются замкнутостью силового многоугольника, т. е. начало первой и конец последней силы совпадают.
. Условиями равновесия
выражаются замкнутостью силового многоугольника, т. е. начало первой и конец последней силы совпадают.
Теорема о трех непараллельных силах: Если под действием трех сил тело находится в
равновесии и линии действия двух сил пересекаются, то все силы лежат в
одной плоскости и их линии действия пересекаются в одной точке.
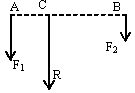
Теория пар сил. Сложение двух
параллельных сил: равнодействующая двух параллельны сил 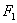 и
и 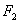 одного направления
имеет такое же направление, ее модуль равен сумме модулей слагаемых сил, а
точка приложения делит отрезок между точками приложения сил на части обратно
пропорциональные модулям сил:
одного направления
имеет такое же направление, ее модуль равен сумме модулей слагаемых сил, а
точка приложения делит отрезок между точками приложения сил на части обратно
пропорциональные модулям сил: 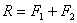 ;
; 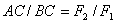 .
.
Равнодействующая двух противоположно направленных
параллельных сил имеет направление силы большей по модулю и модуль, равный
разности модулей сил.
Проекция силы на ось – отрезок,
заключенный между перпендикулярами, проведенными из начала и конца вектора силы
к этой оси. Проекция положительна, если направление отрезка совпадает с
положительным направлением оси.
Проекция силы на плоскость –
вектор на плоскости, заключенный между перпендикулярами, проведенными из начала
и конца вектора силы к этой плоскости.
Парой сил называется система двух параллельных сил,
равных по модулю и направленных в разные стороны. Принятое
обозначение – (![]() ).Под действием пары сил тело будет совершать
вращательное движение.
).Под действием пары сил тело будет совершать
вращательное движение.
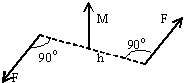
Плечом пары «h»
называется кратчайшее расстояние между линиями действия этих сил.
Момент пары сил 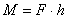 - произведение модуля
одной из сил пары на ее плечо.
- произведение модуля
одной из сил пары на ее плечо.
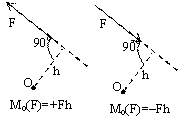
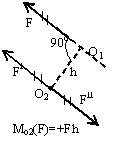
Момент пары сил 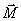 – вектор,
направленный перпендикулярно плоскости сил, так, что, если смотреть ему навстречу,
то видим вращение пары против хода часовой стрелки M>0, и по ходу часовой стрелки M<0 (на рисунке М>0).
– вектор,
направленный перпендикулярно плоскости сил, так, что, если смотреть ему навстречу,
то видим вращение пары против хода часовой стрелки M>0, и по ходу часовой стрелки M<0 (на рисунке М>0).
Теоремы
о парах.
1) Две пары, лежащие в одной плоскости, можно
заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов
данных двух пар 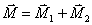 .
.
2) Две пары, имеющие геометрически равные моменты,
эквиваленты.
3)
Не нарушая состояния твердого тела, пару сил можно переносить в плоскости ее
действия. Т.е. момент пары сил является свободным вектором.
4) Система нескольких пар сил эквивалента одной
паре, момент которой равен векторной сумме моментов данных пар. Т.е. система
пар приводится к одной паре, момент которой равен сумме моментов всех пар.
Условие равновесия пар сил:
Пары сил, расположенные в одной плоскости, взаимно уравновешиваются, если
алгебраическая сумма их моментов 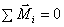 .
.
Момент силы относительно точки
– вектор, численно равный произведению модуля силы на плечо и направленный
перпендикулярно плоскости, содержащей силу и точку, в такую сторону, чтобы смотря ему навстречу, видеть силу стремящейся
повернуться против хода часовой стрелки. Плечо "h"– кратчайшее расстояние от точки до линии
действия силы.
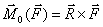 –
момент силы равен векторному произведению вектора
–
момент силы равен векторному произведению вектора 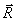 на вектор
на вектор 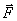 .
.
Модуль векторного произведения: 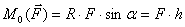 .
.
Для плоской системы сил обычно находят не вектор
момента, а только его модуль: 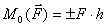 , >0 – против часовой стрелки; <0 – по
часовой стрелке.
, >0 – против часовой стрелки; <0 – по
часовой стрелке.
Свойства
момента силы:
1) момент силы не изменяется при переносе точки
приложения силы вдоль ее линии действия;
2) момент силы относительно точки равен 0 только тогда,
когда сила равна 0 или когда линия действия силы проходит через точку (т.е.
плечо равно 0). Если x,y,z –
координаты точки приложения силы, 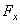 ,
, 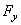 ,
, 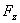 – проекции силы на оси
координат и точка 0 – начало координат, то
– проекции силы на оси
координат и точка 0 – начало координат, то
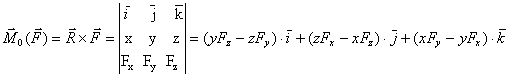 , откуда проекции момента силы на оси координат:
, откуда проекции момента силы на оси координат:  ;
; 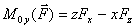 ;
; 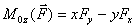 .
.
Главный вектор – векторная
сумма всех сил, приложенных к телу.
Главный момент относительно центра
– векторная сумма моментов всех сил, приложенных к телу относительно того же
центра.
Теорема (лемма) о параллельном переносе силы: сила приложенная в
какой-либо точке твердого тела, эквивалента такой же силе, приложенной в любой
другой точке этого тела, и паре сил, момент которой равен моменту данной силы
относительно новой точки приложения.
План решения задач статики на равновесие сил.
Все задачи на равновесие сил, приложенных к
некоторому телу, решаются по следующему плану:
а) Показываем действующие на тело задаваемые силы.
б) Мысленно освобождаем тело от связей, заменяя их
действие реакциями связей.
в) К полученной системе сил применяем условия
равновесия, соответствующие этой системе.
г) Определяем искомые величины.
Плоская система сил.
Фермы. Силы трения. Пространственная система сил. Центр тяжести
Плоская система сил
Система сил – совокупность сил,
действующих на механическую систему.
Плоская система сил – система сил, расположенных в одной плоскости. Система
сил приводится к одной силе – главному вектору и к паре сил, момент которой
равен главному моменту. Момент пары сил направлен перпендикулярно к плоскости,
в которой лежат силы. В плоских системах нет необходимости использовать
векторное представление момента.
Теорема Вариньона – если
плоская система сил приводится к равнодействующей, то ее момент относительно
какой-либо точки равен алгебраической (т.е. с учетом знака) сумме моментов всех
сил относительно той же точки.
Условия равновесия плоской системы сил:
векторное: 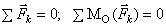 . аналитическое:
. аналитическое: 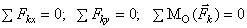 или
или 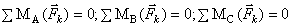 ,
,
где А,В,С – точки,
не лежащие на одной прямой, или 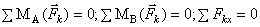 , ось "х" не перпендикулярна отрезку АВ.
, ось "х" не перпендикулярна отрезку АВ.
Условие равновесия сил, приложенных к рычагу. При равновесии сил, приложенных к рычагу,
алгебраическая сумма моментов всех задаваемых сил, относительно опорной точки
равна нулю 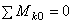 .
.
Коэффициентом устойчивости при опрокидывании принято определять отношением величины
удерживающего момента к величине опрокидывающего момента 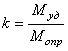 . В случае устойчивого равновесия k > 1.
. В случае устойчивого равновесия k > 1.
Статически определимые задачи.
Задачи, которые можно решать методами статики твёрдого тела, то есть задачи, в
которых число неизвестных не превышает числа уравнений равновесия сил,
называются статически определимыми.
Фермы.
Способ вырезания узлов. Способ
вырезания узлов состоит в том, что мысленно вырезают узлы фермы, прикладывают к
ним соответствующие внешние силы и реакции стержней и составляют по два
уравнения равновесия сил, приложенных к данному узлу. Реакции стержней
направляют от узлов. Если в результате вычислений получат ответ со знаком
минус, то соответствующий стержень сжат.
Леммы
о нулевых стержнях.
Если
усилия в отдельных стержнях загруженной фермы равны нулю, стержни принято
называть нулевыми стержнями.
Лемма 1. Если в незагруженном узле фермы сходятся
два стержня, то усилия в этих стержнях равны нулю.
Лемма 2. Если в незагруженном узле фермы сходятся
три стержня, из которых два расположены по одной прямой, то усилие в третьем
стержне равно нулю. Усилия в двух первых стержнях равны между собой.
Лемма 3. Если в узле фермы сходятся два стержня и к
узлу приложена внешняя сила, линия действия которой совпадает с осью одного из
стержней, то усилие в этом стержне равно по модулю данной силе, а усилие в
другом стержне равно нулю.
Способ
Риттера.
В ферме проводится сечение, рассекающее не более
трёх стержней. Мысленно отбрасываем одну из частей фермы, заменяя её действие
реакциями, направленными по стержням в сторону отброшенной части. Для
определения известных усилий в стержнях составляем уравнения моментов
относительно точек пересечения стержней (точки Риттера). Знак минус при решении
уравнений означает, что стержень сжат.
Равновесие тел при наличии трения.
Закон Кулона (закон Амонтона – Кулона): максимальная сила
сцепления пропорциональна нормальному
давлению тела на плоскость
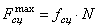 , где
, где 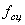 – коэффициент сцепления (зависит от материала, состояния поверхностей,
определяется экспериментально). Направление силы сцепления противоположно
направлению того движения, которое возникло бы при отсутствии сцепления. При
скольжении тела по шероховатой поверхности к нему приложена сила трения скольжения. Ее направление противоположно скорости тела
– коэффициент сцепления (зависит от материала, состояния поверхностей,
определяется экспериментально). Направление силы сцепления противоположно
направлению того движения, которое возникло бы при отсутствии сцепления. При
скольжении тела по шероховатой поверхности к нему приложена сила трения скольжения. Ее направление противоположно скорости тела 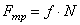 , где f –коэффициент трения скольжения (определяется опытным путем)
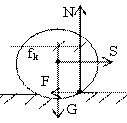
, где f –коэффициент трения скольжения (определяется опытным путем) 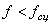 . Реакция шероховатой (реальной) поверхности в отличии от идеально гладкой имеет две составляющие: нормальную
реакцию и силу сцепления (или силу трения при движении). Угол
. Реакция шероховатой (реальной) поверхности в отличии от идеально гладкой имеет две составляющие: нормальную
реакцию и силу сцепления (или силу трения при движении). Угол 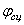 – угол
сцепления (
– угол
сцепления (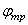 – угол
трения)
– угол
трения) 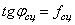 (
(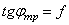 ). Конус с
вершиной в точке касания тел, образующая которого составляет угол сцепления
(угол трения) с нормалью к поверхностям тела называется конусом сцепления (конус трения). Для того чтобы тело начало движение, необходимо (и
достаточно), чтобы равнодействующая активных сил находилась вне конуса трения.
). Конус с
вершиной в точке касания тел, образующая которого составляет угол сцепления
(угол трения) с нормалью к поверхностям тела называется конусом сцепления (конус трения). Для того чтобы тело начало движение, необходимо (и
достаточно), чтобы равнодействующая активных сил находилась вне конуса трения.
Трение качения – сопротивление,
возникающее при качении одного тела по поверхности другого. Причина его
появления в деформации катка и плоскости в точке их соприкосновения и смещения
нормальной реакции в сторону возможного движения. 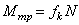 – момент трения
качения,
– момент трения
качения, 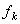 – коэффициент трения качения;
имеет размерность длины.
– коэффициент трения качения;
имеет размерность длины.
Пространственная
система сил.
Пространственная система сил – система
сил, линии действия которых не лежат в одной
плоскости.
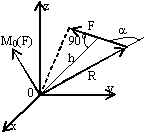
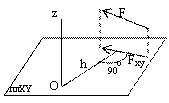
Момент силы относительно оси – скалярная величина, равная моменту проекции этой
силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения
оси с плоскостью. Момент >0, если смотря навстречу
оси, мы видим поворот, который стремится совершить сила направленный против
часовой стрелки 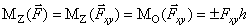 ,
,
На рисунке М>0. Момент силы относительно оси
равен 0: 1) если сила параллельна оси (Fxy=0), 2) если линия действия силы пересекает ось (h=0); т.е. если ось и сила лежат в одной плоскости.
Аналитические выражения моментов силы относительно осей координат: 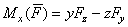 ;
; 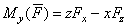 ;
; 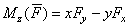 .
.
Приведение пространственной системы сил к данному центру решается с помощью теоремы о параллельном переносе силы. Любая система сил, действующих на абсолютно твердое тело, при
приведении к произвольно взятому центру О заменяется
одной силой R, равной главному вектору
системы и приложенной в центре приведения О, и одной парой с моментом МО,
равным главному моменту системы относительно центра О (главный вектор –
векторная сумма всех сил, приложенных к телу; главный момент относительно
центра – векторная сумма моментов всех сил, приложенных к телу относительно
того же центра).
Статические инварианты пространственной системы сил – такие характеристики этой системы, которые
остаются неизменными при перемене центра приведения.
1-ый инвариант – главный вектор
(квадрат модуля главного вектора): 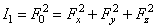 ;
;
2-ой инвариант – скалярное
произведение главного вектора на главный момент: 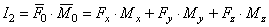 . При перемене центра приведения проекция главного момента на
направление главного вектора
. При перемене центра приведения проекция главного момента на
направление главного вектора 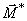 не изменяется
не изменяется 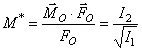 . Совокупность силы
. Совокупность силы 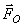 и пары сил, с моментом
и пары сил, с моментом
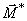 , расположенной в плоскости перпендикулярной линии действия
этой силы, называется динамой
(силовым винтом). Система приводится к
динаме, если второй статический инвариант не равен 0. Прямая,
вдоль которой направлены
, расположенной в плоскости перпендикулярной линии действия
этой силы, называется динамой
(силовым винтом). Система приводится к
динаме, если второй статический инвариант не равен 0. Прямая,
вдоль которой направлены 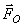 и
и 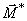 , называется центральной
осью системы сил.
, называется центральной
осью системы сил.
Центральная ось системы сил –
геометрическое место точек пространства, относительно которых главные моменты
заданной системы сил имеют наименьший модуль 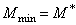 и направлены вдоль
этой оси. Если главный вектор
и направлены вдоль
этой оси. Если главный вектор 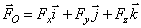 и главный момент
и главный момент 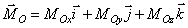 , то уравнения центральной оси:
, то уравнения центральной оси: 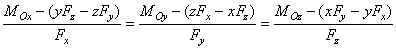 .
.
Случаи
приведения пространственной системы сил:
|
|
|
|
|
Случай приведения
|
1
|
|
|
|
Динама
|
2
|
|
|
|
Равнодействующая
|
3
|
|
|
|
Пара сил
|
4
|
|
|
|
0
|
Условия равновесия пространственной системы
сил:
![]() или
или ![]() .
.
Условия равновесия для системы параллельных сил (||z): 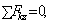
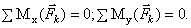
Равнодействующая пространственной системы сходящихся сил: 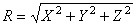 , где
, где 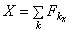 ,
, 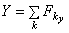 ,
, 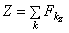 . Направление равнодействующей определяется направляющими
косинусами
. Направление равнодействующей определяется направляющими
косинусами 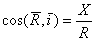 ,
, 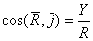 ,
, 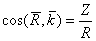 .
.
Центр параллельных сил – точка,
через которую проходит линия действия равнодействующей системы ||-ых сил при любых поворотах этих сил около их точек
приложения в одну и ту же сторону и на один и тот же угол. Координаты центра ||-ых сил: 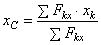 и т.д.
и т.д.
Геометрические характеристики.
Центр тяжести твердого тела –
точка, неизменно связанная с этим телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела при любом
положении тела в пространстве. При этом поле тяжести считается однородным, т.е.
силы тяжести частиц тела параллельны друг другу и сохраняют постоянную величину
при любых поворотах тела. Координаты центра тяжести:
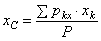 ;
; 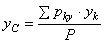 ;
; 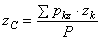 , где
, где 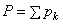 ,
, 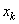 ,
, 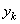 ,
, 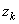 – координаты точек
приложения сил тяжести
– координаты точек
приложения сил тяжести 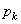 . Центр тяжести – геометрическая точка и может лежать и вне
пределов тела (например, кольцо). Центр тяжести плоской фигуры:
. Центр тяжести – геометрическая точка и может лежать и вне
пределов тела (например, кольцо). Центр тяжести плоской фигуры:
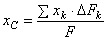 ,
, 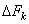 – элементарная
площадка,
– элементарная
площадка, 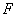 – площадь фигуры. Если
площадь нельзя разбить на несколько конечных
частей, то
– площадь фигуры. Если
площадь нельзя разбить на несколько конечных
частей, то 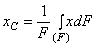 . Центр тяжести: дуги окружности с центральным углом 2a:
. Центр тяжести: дуги окружности с центральным углом 2a: 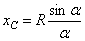 ; кругового сектора:
; кругового сектора: 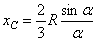 ; треугольник: в точке пересечения медиан (1/3 медианы от
основания).
; треугольник: в точке пересечения медиан (1/3 медианы от
основания).
Статический момент площади плоской фигуры – сумма произведений элементарных площадей, входящих в состав площади
фигуры, на алгебраические значения расстояний до некоторой оси. 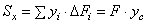 ;
; 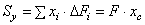 . Статический момент площади
плоской фигуры относительно оси измеряется в см3. Статический момент площади плоской фигуры относительно
оси, проходящей через центр тяжести фигуры, равен нулю.
. Статический момент площади
плоской фигуры относительно оси измеряется в см3. Статический момент площади плоской фигуры относительно
оси, проходящей через центр тяжести фигуры, равен нулю.
Вспомогательные теоремы для определения положения центра тяжести:
Теорема 1. Если однородное тело имеет ось симметрии,
то центр тяжести тела находится на этой оси.
Теорема 2. Если однородное тело имеет плоскость
симметрии, то его центр тяжести находится в этой плоскости.
Теорема 3. Объем тела вращения, полученного
вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей
ее, равен произведению площади фигуры на длину окружности, описанной ее центром
тяжести, 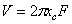 .
.
Теорема 4. Площадь поверхности вращения, полученной вращением
плоской кривой вокруг оси, лежащей в плоскости этой кривой, но не пересекающей
ее, равна произведению длины этой кривой на длину окружности, описанной ее
центром тяжести, 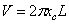 .
.
Определяя
положение центра тяжести плоской фигуры с вырезанной из нее частью, можно
считать площадь этой части отрицательной и тогда: 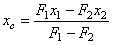 и т.д. — способ отрицательных площадей (объемов).
и т.д. — способ отрицательных площадей (объемов).
Кинематика
Кинематика. Способы
задания движения. Скорость точки. Ускорение точки. Вращательное движение тела.
Кинематика – раздел механики, в
котором изучаются движение материальных тел с геометрической точки зрения, без
учета массы и действующих на них сил. Движущиеся объекты рассматривают как
геометрические точки или геометрические тела. Соответственно изучение делят на
кинематику точки или кинематику твердого тела.
Движение в механике -
механическое движение, т.е. изменение положения тел в пространстве с течением
времени.
Способы задания движения точки: 1)
естественный, 2) координатный, 3) векторный.
Закон движения тела – это зависимость положения тела в пространстве от
времени.
Траектория движения точки -
геометрическое место последовательных положений движущейся точки в
рассматриваемой системе отсчета (непрерывная кривая, которую описывает точка
при своем движении).
Естественный способ указывается
траектория точки, закон ее движения по этой траектории, начало и направление
отсчета дуговой координаты: 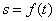 – закон движения
точки. При прямолинейном движении:
– закон движения
точки. При прямолинейном движении: 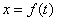 .
.
Дуговая координата –
расстояние, отложенное по траектории движения точки от начала отсчета (НО).
Начало отсчета - неподвижная
точка на траектории, намеченная произвольно, в полном направлении от которой отсчитываются значения 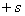 дуговой
координаты; в
другом - отрицательные
дуговой
координаты; в
другом - отрицательные 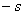 .
.
Радиус кривизны - расстояние по
нормали к траектории в данной точке от местоположения данной точки на
траектории до центра ее кривизны (ЦК) в данной точке траектории.
Кривизна траектории в данной точке
- величина обратная
радиусу кривизны, 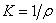 .
.
Вектор
кривизны - 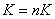 .
.
Длина пути - расстояние,
пройденное точкой по траектории от одного положения на ней до другого.
График движения точки – график
зависимости ее дуговой координаты 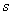 от времени
от времени 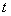 .
.
График пути - путь, пройденный
точкой за некоторый промежуток времени, представляет собой сумму абсолютных
значений элементарных перемещений за этот промежуток времени, т.е. линия этого
графика непрерывно поднимается вверх независимо от направления движения.
Координатный способ положение
точки в пространстве определяется тремя координатами, изменения которых
определяют закон движения точки: 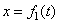 ,
, 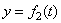 ,
, 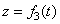 .
.
Если движение в плоскости, то два уравнения
движения. Уравнения движения описывают уравнение траектории в параметрической
форме. Исключив из уравнений параметр t,
получаем уравнение траектории в обычном виде: 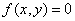 (для плоскости).
(для плоскости).
Векторный способ положение
точки определяется ее радиус-вектором 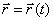 , проведенным из какого-либо центра.
, проведенным из какого-либо центра.
Кривая,
которая вычерчивается концом какого-либо вектора, называется годографом этого вектора. Т.е. траектория – годограф радиус-вектора. Связь между
координатным и векторным способами: 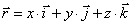 , где
, где 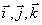 – орты
– единичные вектора, сонаправленные с какой-либо осью.
– орты
– единичные вектора, сонаправленные с какой-либо осью.
модуль 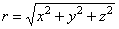 , направляющие косинусы:
, направляющие косинусы: 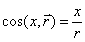 и т.д.
и т.д.
Переход от координатного способа к естественному: 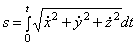 .
.
Скорость движения точки
истинная мгновенная - векторная величина
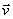 , характеризующая быстроту и направление движения точки в
рассматриваемой системе отсчета.
, характеризующая быстроту и направление движения точки в
рассматриваемой системе отсчета.
Вектор скорости: 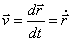 – первая производная
от радиус-вектора по времени (точка обозначает производную по времени);
– первая производная
от радиус-вектора по времени (точка обозначает производную по времени); 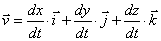 . Проекции скорости:
. Проекции скорости: 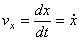 ,
, 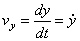 ,
, 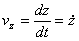 . Модуль скорости:
. Модуль скорости: 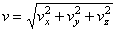 , направляющие косинусы:
, направляющие косинусы: 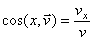 и т.д.
и т.д.
Если
модуль скорости не изменяется с течением времени, то движение называется равномерным. При естественном способе: 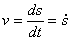 – модуль скорости,
вектор скорости:
– модуль скорости,
вектор скорости: 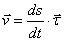 ,
, 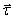 – орт касательной, т.е. скорость всегда направлена по
касательной к траектории. Если v>0, то движение
происходит в сторону положительного отсчета дуговой координаты и наоборот.
– орт касательной, т.е. скорость всегда направлена по
касательной к траектории. Если v>0, то движение
происходит в сторону положительного отсчета дуговой координаты и наоборот.
Движение
в полярной системе координат: 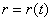 – полярный радиус,
– полярный радиус, 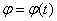 – угол. Проекции
скорости на радиальное направление
– угол. Проекции
скорости на радиальное направление 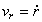 , поперечное направление
, поперечное направление 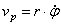 , модуль скорости
, модуль скорости 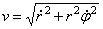 ;
; 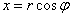 ,
, 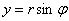 . Для определения алгебраической величины скорости точки по
графику движения в любой момент времени следует провести касательную к графику
движения в соответствующей точке, определить угол
. Для определения алгебраической величины скорости точки по
графику движения в любой момент времени следует провести касательную к графику
движения в соответствующей точке, определить угол 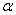 наклона этой касательной к оси t и определить скорость
наклона этой касательной к оси t и определить скорость 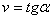 .
.
Ускорение точки истинное
мгновенное - векторная величина, характеризующая быстроту изменения модуля
скорости и направления движения точки. 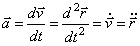 , [м/сек2]. Проекции
ускорения:
, [м/сек2]. Проекции
ускорения: 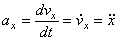 и т.д. Модуль ускорения:
и т.д. Модуль ускорения: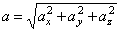 , направляющие
косинусы:
, направляющие
косинусы: 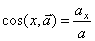 , и т.д.
, и т.д.
При задании движения в полярных координатах:
проекции ускорения на радиальное направление 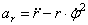 , поперечное направление
, поперечное направление 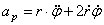 , модуль ускорения
, модуль ускорения 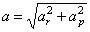 . При естественном способе задания движения полное ускорение
раскладывают на нормальное и касательное
(тангенциальное) ускорения:
. При естественном способе задания движения полное ускорение
раскладывают на нормальное и касательное
(тангенциальное) ускорения: 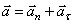 . Модуль
нормального ускорения:
. Модуль
нормального ускорения: 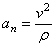 ,
, 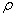 – радиус кривизны
траектории, нормальное ускорение направлено по нормали к траектории (
– радиус кривизны
траектории, нормальное ускорение направлено по нормали к траектории (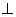 к касательной) всегда к центру кривизны, т.е. в сторону
вогнутости. Нормальное ускорение характеризует изменение скорости по
направлению. Нормальное ускорение в данный момент времени может быть равно нулю
к касательной) всегда к центру кривизны, т.е. в сторону
вогнутости. Нормальное ускорение характеризует изменение скорости по
направлению. Нормальное ускорение в данный момент времени может быть равно нулю
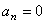 в том случае, когда в
данный момент скорость точки обращается в нуль (точка
меняет направление движения), или, когда движущаяся точка находится в точке
перегиба своей траектории
в том случае, когда в
данный момент скорость точки обращается в нуль (точка
меняет направление движения), или, когда движущаяся точка находится в точке
перегиба своей траектории 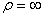 .
.
Модуль
касательного ускорения 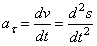 , направлено по касательной к траектории, либо в сторону
скорости, либо в обратную. Касательное ускорение
характеризует изменение скорости по величине. При ускоренном движении
направление касательного ускорения и скорости совпадают, при замедленном –
противоположно.
, направлено по касательной к траектории, либо в сторону
скорости, либо в обратную. Касательное ускорение
характеризует изменение скорости по величине. При ускоренном движении
направление касательного ускорения и скорости совпадают, при замедленном –
противоположно. 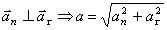 .
Вектор ускорения лежит в соприкасающейся плоскости, т.е. его проекция на
бинормаль равна 0 (главная нормаль лежит в соприкасающейся плоскости, т.е. в
плоскости плоской кривой, бинормаль –
.
Вектор ускорения лежит в соприкасающейся плоскости, т.е. его проекция на
бинормаль равна 0 (главная нормаль лежит в соприкасающейся плоскости, т.е. в
плоскости плоской кривой, бинормаль – 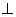 к главной нормали и касательной). Направление ускорения
определяется углом
к главной нормали и касательной). Направление ускорения
определяется углом 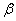 между вектором
между вектором 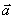 и главной нормалью
и главной нормалью 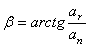 .
.
Частные случаи движения точки:
1)
Прямолинейное движение: радиус кривизны 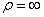 (бесконечно большой),
отсюда
(бесконечно большой),
отсюда 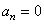 ,
, 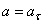 ..
..
2)
Равномерное криволинейное
движение: 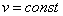 , отсюда
, отсюда 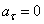 ,
,  . Ускорение
появляется только за счет изменения направления скорости. Закон движения:
. Ускорение
появляется только за счет изменения направления скорости. Закон движения: 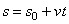 , при
, при 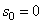 ,
, 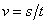 .
.
3)
Равномерное прямолинейное
движение: 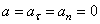 . Единственное движение, где
. Единственное движение, где 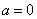 .
.
4)
Равнопеременное криволинейное
движение: 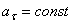 ,
, 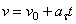 ,
, 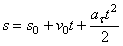 .
.
При равноускоренном движении знаки у 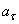 и
и 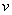 одинаковы, при
равнозамедленном – разные.
одинаковы, при
равнозамедленном – разные.
Простейшие движения твердого тела: поступательное и
вращение вокруг неподвижной оси, плоскопараллельное
(плоское), сферическое и общий случай движения твёрдого тела.
Поступательное движение тела – такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.
Вращательное движение тела – такое движение твердого тела, при котором все
точки, принадлежащие некоторой прямой, неизменно связанной с телом, остаются
неподвижными. Эта прямая
называется осью вращения тела. При этом движении все точки тела движутся в
плоскостях, перпендикулярных оси вращения, и описывают окружности, центры
которых лежат на оси вращения. Уравнение (закон) вращательного движения: 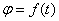 – угол поворота тела в
радианах. (
– угол поворота тела в
радианах. (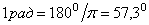 ).
).
Угол поворота (угловая
координата) - двугранный угол, образованный полуплоскостями, проходящими через
ось вращения, одна P из которых неподвижна,
а другая Q вращается вокруг оси вместе с телом. В одном направлении вокруг оси
отсчитываются положительные значения угла 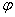 , в другом - отрицательные.
, в другом - отрицательные.
Угловая скорость: 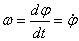 , [рад/с] – определяет быстроту изменения угла поворота.
, [рад/с] – определяет быстроту изменения угла поворота.
Вектор угловой скорости тела, совершающего вращение
вокруг неподвижной оси, направлен вдоль оси вращения так, что если смотреть ему
навстречу вращение будет против часовой стрелки. "n"– число оборотов в
мин. [об/мин], 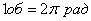 ,
, 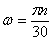 .
.
Угловое ускорение тела: 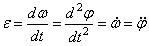 , [рад/с2]. Вектор
углового ускорения также направлен вдоль оси вращения. При ускоренном движении
совпадает по направлению с угловой скоростью и противоположно при замедленном
вращении.
, [рад/с2]. Вектор
углового ускорения также направлен вдоль оси вращения. При ускоренном движении
совпадает по направлению с угловой скоростью и противоположно при замедленном
вращении.
Частные случаи вращения тела: 1)
Равномерное вращение: 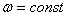 ,
, 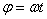 ,
, 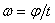 ,
,
2) Равнопеременное вращение: 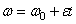 ;
; 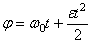 , здесь начальный угол
, здесь начальный угол 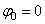 .
.
Скорости и ускорения точек вращающегося тела. 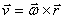 – скорость любой точки
твердого тела, вращающегося вокруг неподвижной оси, равна векторному
произведению вектора угловой скорости тела на радиус–вектор
этой точки. Модуль векторного произведения:
– скорость любой точки
твердого тела, вращающегося вокруг неподвижной оси, равна векторному
произведению вектора угловой скорости тела на радиус–вектор
этой точки. Модуль векторного произведения: 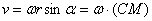 , где (СМ) – расстояние от точки М до оси вращения. Направлен
вектор скорости по касательной к окружности, по которой перемещается точка М, в
сторону вращения.
, где (СМ) – расстояние от точки М до оси вращения. Направлен
вектор скорости по касательной к окружности, по которой перемещается точка М, в
сторону вращения.
Формулы
Эйлера: 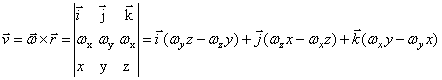 ,
,
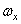 ,
, 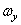 ,
, 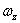 – проекции вектора угловой скорости. Проекция
вращательной (окружной) скорости:
– проекции вектора угловой скорости. Проекция
вращательной (окружной) скорости: 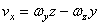 ;
; 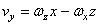 ;
; 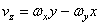 . Если ось вращения совпадает с осью z, то
. Если ось вращения совпадает с осью z, то 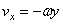 ;
; 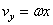 . Ускорение:
. Ускорение:  .
.
Вращательное ускорение 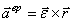 , модуль вращательного ускорения
, модуль вращательного ускорения 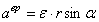 , направлено по касательной к траектории точки, т.е.
параллельно скорости.
, направлено по касательной к траектории точки, т.е.
параллельно скорости.
Центростремительное (осестремительное) ускорение 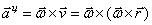 ,
, 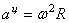 , направлено по радиусу к оси (центру) вращения. Модуль
полного ускорения:
, направлено по радиусу к оси (центру) вращения. Модуль
полного ускорения: 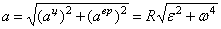 . Угол, между векторами полного и центростремительного
ускорений:
. Угол, между векторами полного и центростремительного
ускорений: 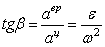 . Проекции ускорения точек тела вращающегося вокруг оси
. Проекции ускорения точек тела вращающегося вокруг оси 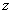 :
: 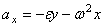 ,
,
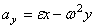 ,
, 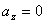 .
.
Плоское движение
твердого тела. Сферическое движение твердого тела. Движение свободного твердого
тела.
Плоское движение твердого тела
Плоским (плоскопараллельным)
называется такое движение, при котором все его точки перемещаются параллельно
некоторой неподвижной плоскости.
Уравнения плоского движения: 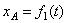 ,
, 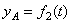 ,
, 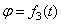 , точка А называется
полюсом. Плоское движение твердого тела слагается из поступательного движения,
при котором все точки тела движутся так же, как полюс (А),и
из вращательного движения вокруг этого полюса. Поступательное перемещение
зависит от выбора полюса, а величина и направление угла поворота не зависят.
, точка А называется
полюсом. Плоское движение твердого тела слагается из поступательного движения,
при котором все точки тела движутся так же, как полюс (А),и
из вращательного движения вокруг этого полюса. Поступательное перемещение
зависит от выбора полюса, а величина и направление угла поворота не зависят.
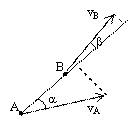
Скорости точек тела при плоском движении: 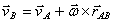 ;
; 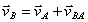 ,
, 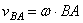 , т.е. скорость какой-либо точки В
плоской фигуры равна геометрической сумме скорости полюса А и
скорости точки В при вращении плоской фигуры вокруг полюса А.
, т.е. скорость какой-либо точки В
плоской фигуры равна геометрической сумме скорости полюса А и
скорости точки В при вращении плоской фигуры вокруг полюса А.
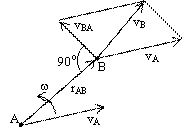
Теорема о проекциях скоростей двух точек тела: при плоском движении проекции скоростей двух точек
тела на ось, проходящую через эти точки, равны между собой: 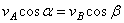 . Концы скоростей
точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные
расстояниям между соответствующими точками.
. Концы скоростей
точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные
расстояниям между соответствующими точками.
Мгновенный центр скоростей –
точка плоской фигуры, скорость которой в данный момент равна нулю – Р. Если
тело движется непоступательно, т.е. 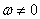 , то мгновенный центр скоростей всегда существует. При
поступательном движении м.ц.с. находится в
, то мгновенный центр скоростей всегда существует. При
поступательном движении м.ц.с. находится в 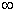 .
. 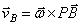 – скорость любой точки
плоской фигуры имеет модуль, равный произведению угловой скорости фигуры на
длину отрезка, соединяющего точку с м.ц.с., и направлена
– скорость любой точки
плоской фигуры имеет модуль, равный произведению угловой скорости фигуры на
длину отрезка, соединяющего точку с м.ц.с., и направлена 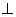 этому отрезку в
сторону вращения фигуры.
этому отрезку в
сторону вращения фигуры. 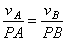 , скорости точек тела
пропорциональны их расстояниям до м.ц.с.
, скорости точек тела
пропорциональны их расстояниям до м.ц.с. 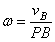 , угловая скорость тела равна отношению скорости какой-нибудь
точки к ее расстоянию до м.ц.с.
, угловая скорость тела равна отношению скорости какой-нибудь
точки к ее расстоянию до м.ц.с.
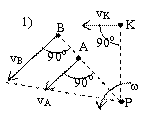
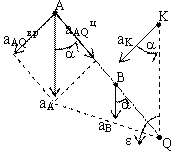
Определение положения м.ц.с.: 1) м.ц.с. – точка
пересечения перпендикуляров, восстановленных к скоростям точек (например в точке В и точке К);
2) если скорости точек А и
В параллельны между собой и
перпендикулярны АВ, то для определения м.ц.с. должны быть известны модули и
направления скоростей (см. 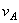 и
и 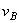 );
);
3) если они при этом равны между
собой, то м.ц.с. находится в 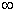 , а угловая скорость
, а угловая скорость 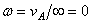 ;
;
4) если известно, что скорости двух точек А и В равны, параллельны и не перпендикулярны АВ, то м.ц.с.
в 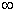 , и угловая скорость
, и угловая скорость 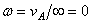 , если это имеет место только к некоторый момент времени, то
имеем мгновенное поступательное движение;
, если это имеет место только к некоторый момент времени, то
имеем мгновенное поступательное движение;
5) если плоская фигура катится без скольжения по
неподвижной поверхности, то м.ц.с. плоской фигуры будет в точке соприкасания.
Теорема Шаля: плоскую фигуру можно переместить из одного положения в любое другое
положение на плоскости одним поворотом этой фигуры вокруг некоторого
неподвижного центра. Этот центр на неподвижной плоскости, совпадает с м.ц.с. и называется мгновенным центром вращений (ось вращений). При движении плоской фигуры м.ц.с. непрерывно
изменяет свое положение. Геометрическое место м.ц.с.,
отмеченных на неподвижной плоскости, называется неподвижной центроидой.
Геометрическое место м.ц.с., отмеченных на плоскости фигуры, называется подвижной центроидой (колесо катится по прямой: неподвижная центроида – прямая, подвижная –
окружность). При движении плоской фигуры подвижная центроида катится без
скольжения по неподвижной центроиде (теорема Пуансо).
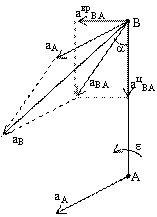
Ускорения точек тела при плоском движении: 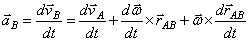 ,
,
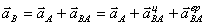 – ускорение любой
точки (В) фигуры геометрически складывается из ускорения полюса (А) и центростремительного и вращательного ускорений во вращательном движении тела относительно
полюса.
– ускорение любой
точки (В) фигуры геометрически складывается из ускорения полюса (А) и центростремительного и вращательного ускорений во вращательном движении тела относительно
полюса. 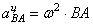 ,
, 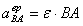 ,
, 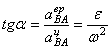 ,
, 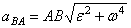 .
.
Следствие 1: Проекция ускорения любой точки плоской
фигуры на ось, проведённую из произвольного полюса через эту точку, не может
быть больше проекции ускорения полюса на ту же ось.
Следствие 2: Концы ускорений точек неизменяемого
отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные
расстояниям между этими точками.
Мгновенный центр ускорений (м.ц.у.) – точка (Q) плоской фигуры,
ускорение которой в данный момент времени равно нулю.
Для его построения из точки А откладываем под углом 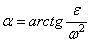 к ускорению
к ускорению 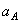 отрезок
отрезок 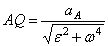 , при этом угол откладывается от ускорения в сторону,
направления углового ускорения
, при этом угол откладывается от ускорения в сторону,
направления углового ускорения 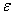 . Модули ускорений точек плоской фигуры пропорциональны
расстояниям от этих точек до м.ц.у., а векторы ускорений составляют с
отрезками, соединяющими эти точки и м.ц.у. один и тот же угол
. Модули ускорений точек плоской фигуры пропорциональны
расстояниям от этих точек до м.ц.у., а векторы ускорений составляют с
отрезками, соединяющими эти точки и м.ц.у. один и тот же угол 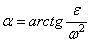 :
: 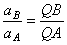 . Мгновенный центр скоростей Р и
мгновенный центр ускорений Q являются различными точками плоской фигуры.
. Мгновенный центр скоростей Р и
мгновенный центр ускорений Q являются различными точками плоской фигуры.
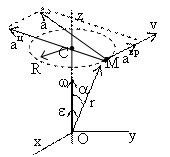
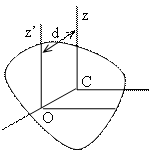
Сферическое движение твердого тела
Сферическое движение – движение
твердого тела, одна из точек которого во все время движения остается
неподвижной (например, движение волчка). Точки тела движутся по сферическим
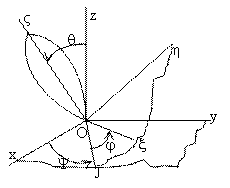
поверхностям. Положение тела определяют при помощи трех углов. Для этого
задаются две системы координат: неподвижная Оxyz и
подвижная 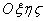 , связанная с твердым телом. Линия ОJ –
линия узлов, задаются углы:
, связанная с твердым телом. Линия ОJ –
линия узлов, задаются углы: 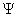 – угол прецессии,
– угол прецессии, 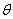 – угол нутации,
– угол нутации, 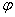 – угол собственного вращения — углы
Эйлера. Таким образом, уравнения
сферического движения:
– угол собственного вращения — углы
Эйлера. Таким образом, уравнения
сферического движения: 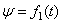 ;
; 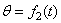 ;
; 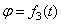 . Углы отсчитываются от осей против хода часовой
стрелки.
. Углы отсчитываются от осей против хода часовой
стрелки.
Теорема Эйлера-Даламбера: всякое
перемещение тела, имеющего неподвижную точку, можно заменить одним поворотом
вокруг некоторой мгновенной оси вращения, проходящей через эту точку. Скорости
всех точек тела, лежащих на мгновенной оси вращения в данный момент времени
равны нулю. Вектор угловой скорости (мгновенной угловой
скорости) откладывается о неподвижной
точки по мгновенной оси в такую сторону, чтобы, смотря навстречу этому вектору,
видеть вращение происходящим против часовой стрелки. Вектор угловой
скорости со временем изменяется не только по численной величине, но и по
направлению. Конец вектора описывает годограф скорости вектора 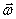 . Угловое ускорение:
. Угловое ускорение: 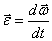 – скорость конца
вектора
– скорость конца
вектора 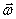 , совпадает по направлению с касательной к годографу вектора
угловой скорости.
, совпадает по направлению с касательной к годографу вектора
угловой скорости.
В случае сферического движения в отличии от случая вращения вокруг неподвижной оси вектор 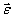 не совпадает с
направлением
не совпадает с
направлением 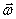 . Скорости точек при сферическом движении:
. Скорости точек при сферическом движении: 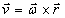 – векторное
произведение,
– векторное
произведение, 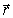 – радиус-вектор точки, проведенный из неподвижной точки,
модуль
– радиус-вектор точки, проведенный из неподвижной точки,
модуль 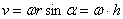 , h –
расстояние от точки до мгновенной оси вращения.
, h –
расстояние от точки до мгновенной оси вращения.
Формулы Эйлера:
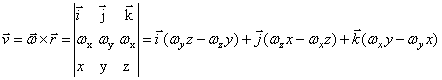 .
.
Ускорения: 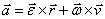 , вращательное ускорение
, вращательное ускорение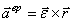 модуль вращательного ускорения
модуль вращательного ускорения 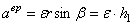 ,
, 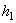 - расстояние от точки до вектора
- расстояние от точки до вектора 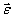 , направлено
, направлено 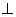 –но плоскости, проходящей через
точку М и вектор
–но плоскости, проходящей через
точку М и вектор 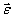 .
.
Осестремительное ускорение 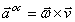 ,
, 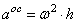 , направлено к оси вращения.
, направлено к оси вращения.
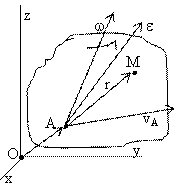
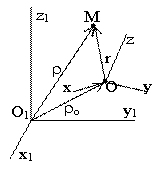
Движение свободного твердого тела (общий случай движения). Свободное твердое тело имеет шесть степеней
свободы. При рассмотрении движения свободного твердого тела, кроме неподвижной
системы координат Oxyz, вводится
подвижная система координат Ax1y1z1, которая связана с телом в
точке А. Тогда движение свободного
твердого тела представляет собой сложное движение, которое можно
рассматривать как состоящее из поступательного движения вместе с полюсом (А) и
сферического движения вокруг полюса. Уравнения движения свободного твердого
тела: 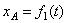 ;
; 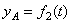 ;
; 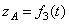 ;
; 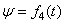 ;
; 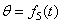 ;
; 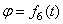 (углы Эйлера).
Первые три уравнения определяют поступательную часть движения и зависят от
выбора полюса, остальные три определяют сферическое движение вокруг полюса и от
выбора полюса не зависят. Скорость любой точки свободного твердого тела = геометрической
сумме скорости полюса и скорости этой точки в ее сферическом движении вокруг
полюса.
(углы Эйлера).
Первые три уравнения определяют поступательную часть движения и зависят от
выбора полюса, остальные три определяют сферическое движение вокруг полюса и от
выбора полюса не зависят. Скорость любой точки свободного твердого тела = геометрической
сумме скорости полюса и скорости этой точки в ее сферическом движении вокруг
полюса. 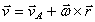
Ускорение точки свободного твердого тела = геометрической
сумме ускорения полюса, осестремительного ускорения точки и ее вращательного
ускорения, определенных относительно мгновенной оси и
оси углового ускорения, проходящих через полюс.
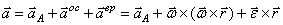 , два последних члена дают ускорение точки в ее движении
вокруг полюса.
, два последних члена дают ускорение точки в ее движении
вокруг полюса.
Сложное движение
точки. Сложное движение твердого тела.
Сложное движение точки (тела) –
такое движение, при котором точка (тело) одновременно участвует в нескольких
движениях (например, пассажир, перемещающийся по движущемуся вагону). В этом
случае вводится подвижная система координат (Oxyz), которая совершает заданное движение относительно
неподвижной (основной) системы координат (O1x1y1z1).
Абсолютным движением точки
называется движение по отношению к неподвижной системе координат.
Абсолютная скорость точки равна
геометрической сумме переносной и относительной скоростей: 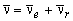 .
.
Абсолютное ускорение точки
равно геометрической сумме переносного, относительного и кориолисового
ускорений: 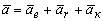
Относительное движение –
движение по отношению к подвижной системе координат (движение по вагону).
Относительная скорость, ускорение точки - скорость, ускорение относительного движения точки.
Переносное движение – движение
подвижной системы координат относительно неподвижной (движение вагона).
Переносная скорость, ускорение точки - скорость, ускорение в движении относительно земли той точки тела, в
которой в данный момент времени находится рассматриваемая материальная точка.
Теорема о сложении скоростей:
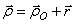 ,
, 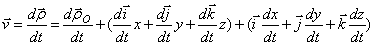 ;
; 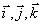 -орты (единичные вектора) подвижной системы координат, орт
вращается вокруг мгновенной оси, поэтому скорость его конца
-орты (единичные вектора) подвижной системы координат, орт
вращается вокруг мгновенной оси, поэтому скорость его конца 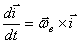 и т.д.
и т.д.
Отсюда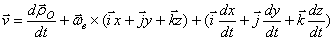 ,
,
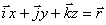 ;
; 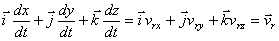 – относительная скорость.
– относительная скорость.
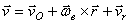 ; переносная скорость:
; переносная скорость: 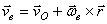 , поэтому абсолютная скорость точки = геометрической сумме ее
переносной (
, поэтому абсолютная скорость точки = геометрической сумме ее
переносной (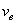 ) и относительной (
) и относительной (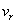 ) скоростей
) скоростей 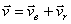 , модуль:
, модуль: 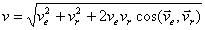 .
.
Теорема о сложении ускорений (теорема Кориолиса):
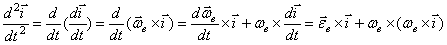 и т.д.
и т.д.
Слагаемые выражения, определяющего ускорения 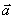 : 1)
: 1) 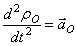 – ускорение полюса О;
– ускорение полюса О;
2) 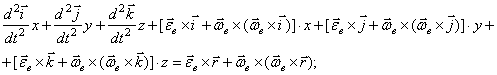
3) 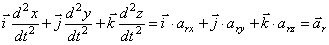 – относительное ускорение точки;
– относительное ускорение точки;
4) 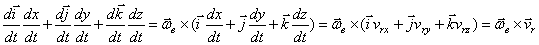 ,
,
получаем: 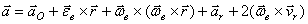 .
.
Первые три слагаемых представляют собой ускорение
точки в переносном движении: 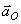 – ускорение полюса О;
– ускорение полюса О; 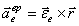 – вращательное ускорение,
– вращательное ускорение, 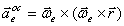 –
осестремительное ускорение, т.е.
–
осестремительное ускорение, т.е. 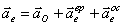 .
.
Ускорение Кориолиса (кориолисово ускорение): 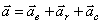 , где
, где 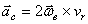 – в
случае непоступательного переносного движения абсолютное ускорение =
геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует: 1) изменение модуля и
направления переносной скорости точки из-за ее относительного движения; 2) изменение
направления относительной скорости точки из-за вращательного переносного
движения. Модуль ускорения Кориолиса:
– в
случае непоступательного переносного движения абсолютное ускорение =
геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует: 1) изменение модуля и
направления переносной скорости точки из-за ее относительного движения; 2) изменение
направления относительной скорости точки из-за вращательного переносного
движения. Модуль ускорения Кориолиса: 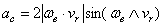 , направление вектора
, направление вектора 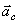 определяется по
правилу векторного произведения, или по правилу Жуковского: проекцию
относительной скорости на плоскость, перпендикулярную переносной угловой
скорости, надо повернуть на 90о в направлении вращения.
определяется по
правилу векторного произведения, или по правилу Жуковского: проекцию
относительной скорости на плоскость, перпендикулярную переносной угловой
скорости, надо повернуть на 90о в направлении вращения.
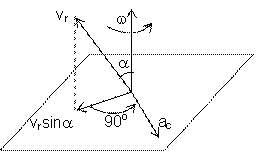
Кориолисово ускорение = 0 в трех
случаях: 1) 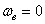 , т.е. в случае поступательного переносного движения или в
момент обращения угловой скорости в 0; 2)
, т.е. в случае поступательного переносного движения или в
момент обращения угловой скорости в 0; 2) 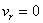 ; 3)
; 3) 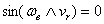 , т.е.
, т.е. 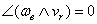 , когда относительная скорость
, когда относительная скорость 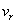 параллельна оси переносного вращения.
параллельна оси переносного вращения.
В случае движения в одной плоскости – угол между 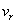 и вектором
и вектором 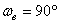 ,
, 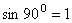 ,
, 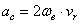 .
.
Сложное движение твердого тела.
При сложении двух поступательных движений результирующее движение также
является поступательным и скорость результирующего движения равна сумме
скоростей составляющих движений. Сложение вращений тв. тела вокруг
пересекающихся осей. Ось вращения, положение которой в пространстве изменяется
со временем назыв. мгновенной
осью вращения тела. Вектор угловой
скорости – скользящий вектор, направленный вдоль мгновенной оси вращения.
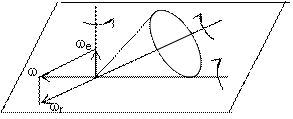
Абсолютная угловая скорость тела = геометрической сумме скоростей составляющих
вращений – правило
параллелограмма угловых скоростей.
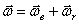 . Если тело участвует
одновременно в мгновенных вращениях вокруг нескольких осей, пересекающихся в
одной точке, то
. Если тело участвует
одновременно в мгновенных вращениях вокруг нескольких осей, пересекающихся в
одной точке, то 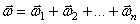 . При сферическом
движении твердого тела, одна из точек которого во все время движения остается неподвижной,
имеем уравнения сферического движения:
. При сферическом
движении твердого тела, одна из точек которого во все время движения остается неподвижной,
имеем уравнения сферического движения: 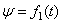 ;
; 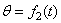 ;
; 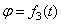 ,
, 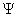 – угол
прецессии,
– угол
прецессии, 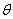 – угол нутации,
– угол нутации, 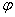 – угол собственного
вращения — углы Эйлера. Угловая скорость прецессии
– угол собственного
вращения — углы Эйлера. Угловая скорость прецессии 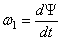 , угл. скорость нутации
, угл. скорость нутации 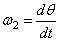 , угл. ск. собственного вращения
, угл. ск. собственного вращения 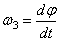 .
.  ,
,
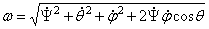 –
модуль угловой скорости тела вокруг мгновенной оси. Через проекции на неподвижные
оси координат:
–
модуль угловой скорости тела вокруг мгновенной оси. Через проекции на неподвижные
оси координат: 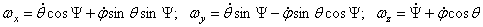 – кинематические уравнения Эйлера.
– кинематические уравнения Эйлера.
Сложение вращений вокруг 2-х параллельных осей.
Вращения направлены в одну сторону. 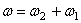 , С – мгновенный центр скоростей и через нее проходит
мгновенная ось вращения,
, С – мгновенный центр скоростей и через нее проходит
мгновенная ось вращения, 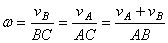 ,
, 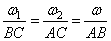 .
.
2) Вращения направлены в разные стороны. 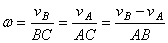 ,
, 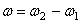
С – мгн. центр ск. и
мгн. ось вращения, 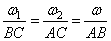 . Векторы угловых скоростей при вращении вокруг ||-ых осей складываются так же, как векторы параллельных сил.
. Векторы угловых скоростей при вращении вокруг ||-ых осей складываются так же, как векторы параллельных сил.
3)
Пара вращений – вращения вокруг ||-ных
осей направлены в разные стороны и угловые скорости по модулю равны (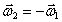 – пара
угловых скоростей). В этом случае
– пара
угловых скоростей). В этом случае 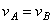 , результирующее движение тела – поступательное (или
мгновенное поступательное) движение со скоростью
, результирующее движение тела – поступательное (или
мгновенное поступательное) движение со скоростью 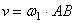 – момент пары угловых скоростей (поступательное движение педали велосипеда относит-но рамы). Мгн. центр скоростей находится в
бесконечности.
– момент пары угловых скоростей (поступательное движение педали велосипеда относит-но рамы). Мгн. центр скоростей находится в
бесконечности.
Сложение поступательного и вращательного
движений. 1) Скорость поступательного
движения 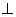 к оси вращения –
плоскопараллельное движение – мгновенное вращение вокруг оси Рр с угловой
скоростью
к оси вращения –
плоскопараллельное движение – мгновенное вращение вокруг оси Рр с угловой
скоростью  .
.
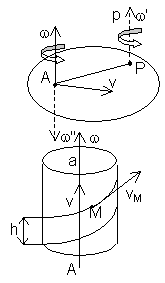
2)
Винтовое движение – движение тела слагается из вращательного движения
вокруг оси Аа с угл.ск. 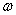 и поступательного со скоростью v||Аа.
Ось Аа – ось винта. Если
и поступательного со скоростью v||Аа.
Ось Аа – ось винта. Если 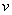 и
и 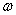 в одну сторону, то
винт – правый, если в разные – левый. Расстояние,
проходимое за время одного оборота любой точкой тела, лежащей на оси винта,
наз. шагом винта – h. Если
в одну сторону, то
винт – правый, если в разные – левый. Расстояние,
проходимое за время одного оборота любой точкой тела, лежащей на оси винта,
наз. шагом винта – h. Если 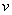 и
и 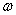 постоянны, то
постоянны, то 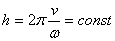 , при постоянном шаге любая
точка М, не лежащая на оси винта
описывает винтовую линию.
, при постоянном шаге любая
точка М, не лежащая на оси винта
описывает винтовую линию. 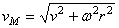 направлена
по касательной к винтовой линии.
направлена
по касательной к винтовой линии.
3)
Скорость поступательного движения образует произвольный угол с осью вращения, в
этом случае движение можно рассматривать как слагающееся из серии мгновенных
винтовых движений, вокруг непрерывно изменяющихся винтовых осей – мгновенно–винтовое движение.
Динамика
Динамика. Основные
законы механики. Колебательное движение материальной точки.
Динамика – раздел механики, в котором
изучаются законы движения материальных тел под действием сил. В динамике
решаются два типа задач. Первая состоит в определении действующих сил при
заданном законе движения материального объекта (точки или системы). Вторая
задача обратная первой: определяется закон движения материального объекта при
известных действующих на него силах.
Осн.законы механики (зак-ны
Галилея-Ньютона):
Закон инерции (1-ый закон):
материальная точка сохраняет состояние покоя или равномерного прямолинейного
движения до тех пор, пока действие других тел не изменит это состояние;
Инерция (инерционность) -
свойство материальных тел, заключающееся в стремлении их сохранять неизменной скорость своего движения (или состояние покоя),
т.е. сохранять данное кинематическое состояние.
Сила инерции материальной точки
представляет собой противодействие материальной точки изменению ее скорости и
приложена к телу, сообщающему этой точке ускорение. Сила инерции равна по
модулю произведению массы материальной точки на модуль ее ускорения и направлена
в сторону, противоположную ускорению 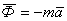 . При неравномерном криволинейном движении точки силу
инерции, представленной в виде касательной (
. При неравномерном криволинейном движении точки силу
инерции, представленной в виде касательной (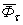 ), и нормальной (
), и нормальной (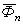 ) силами инерции. Эти силы направлены
противоположно касательному и нормальному ускорению
) силами инерции. Эти силы направлены
противоположно касательному и нормальному ускорению 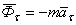 ,
, 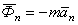 ,
, 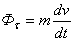 ,
, 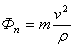 . В случае
равномерного движения точки по кривой
. В случае
равномерного движения точки по кривой 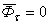 . В случае равномерного движения точки по прямой
. В случае равномерного движения точки по прямой 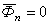 . Если точка принадлежит твердому телу, вращающемуся вокруг
неподвижной оси, то модуль ее вращательной и центробежной сил инерции
определяется по формулам:
. Если точка принадлежит твердому телу, вращающемуся вокруг
неподвижной оси, то модуль ее вращательной и центробежной сил инерции
определяется по формулам: 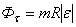 ,
, 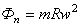 , где
, где 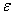 ,
, 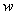 — угловое ускорение и
угловая скорость тела.
— угловое ускорение и
угловая скорость тела.
Мерой инерции материальных тел являются: масса (при поступательном
движении); момент инерции (при вращении).
Масса - количество материи
данного вида в данной точке (в данном объеме) или количественная мера
инерционности тела. Единица измерения массы - килограмм (кг).
Масса определяет инерционность тела только при
поступательном движении, так как в этом случае скорости и ускорения всех
точек тела в данный момент времени геометрически равны. При вращении вокруг оси
инерционность тела определяется не только массой тела, но и тем как масса
распределена окрест оси вращения. Чем компактнее (ближе к оси) распределена
масса тела, тем меньше инерционность тела и наоборот. Поэтому при вращении тела
вокруг оси его инерционность определяет момент инерции тела. Определяют моменты инерции тела относительно:
точки (начала декартовой системы координат); оси (координатных осей); плоскости
(координатных плоскостей).
Основной закон динамики ( 2-ой закон (Ньютона)): ускорение матер.точки
пропорционально приложенной к ней силе и имеет одинаковое с ней
направление 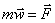 ;
;
Законы инерции и пропорциональности силы и ускорения
справедливы для инерциальных систем отсчета.
Система
отсчета, в которой проявляются 1-ый и 2-ой законы, назыв. инерциальной системой отсчета. Для большинства задач за такую систему отсчета можно
принять систему осей, связанных с Землей.
Закон равенства действия и противодействия (3-й закон (Ньютона)): всякому действию соответствует равное и противоположно направленное противодействие;
Закон независимости сил:
несколько одновременно действующих на матер.точку сил
сообщают точке такое ускорение, какое сообщила бы ей одна сила, равная их
геометрической сумме. В классической механике масса движущегося тела
принимается равной массе покоящегося тела, – мера инертности тела и его
гравитационных свойств. Масса = весу тела, деленному на ускорение свободного падения. 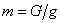 , где g»9,81м/с2. g зависит
от географической широты места и высоты над уровнем моря – не постоянная величина,
то в отличие от массы тела его вес не является
постоянной величиной. Наибольший вес тело имеет на полюсе, а
наименьший на экваторе.
, где g»9,81м/с2. g зависит
от географической широты места и высоты над уровнем моря – не постоянная величина,
то в отличие от массы тела его вес не является
постоянной величиной. Наибольший вес тело имеет на полюсе, а
наименьший на экваторе.
Сила – 1Н (Ньютон) = 1кг×м/с2.
Дифференциальные уравнения движения
материальной точки: 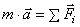 , в проекции на декартовы оси коорд.:
, в проекции на декартовы оси коорд.: 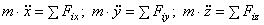 , на оси естественного трехгранника:
, на оси естественного трехгранника: 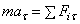 ;
; 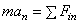 ;
; 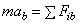 (
(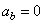 – проекция
ускорения на бинормаль), т.е.
– проекция
ускорения на бинормаль), т.е. 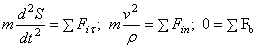 (
(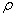 – радиус кривизны траектории в текущей точке). В случае
плоского движения точки в полярных координатах:
– радиус кривизны траектории в текущей точке). В случае
плоского движения точки в полярных координатах: 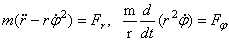 .
.
Две основные задачи динамики:
При решении этих задач исходными являются
дифференциальные уравнения движения точки, записанные в общем
виде в декартовых или естественных координатах.
Первая задача динамики – зная
закон движения точки, определить действующую на нее силу;
Вторая задача динамики (основная)
– зная действующие на точку силы, определить закон движения точки.
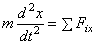 – дифференциальное
ур-ие прямолинейного движения точки. Дважды интегрируя его, находим общее
решение
– дифференциальное
ур-ие прямолинейного движения точки. Дважды интегрируя его, находим общее
решение 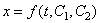 .
.
Постоянные интегрирования C1, C2 ищут
из начальных условий: t=0, x=x0, 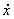 =Vx=V0, x=f(t,x0,V0) –
частное решение – закон движения точки.
=Vx=V0, x=f(t,x0,V0) –
частное решение – закон движения точки.
Принцип относительности
классической механики можно сформулировать так: никакие механические явления,
происходящие в среде, не могут обнаружить ее прямолинейного и равномерного
поступательного движения.
Материальная точка находится в состоянии
относительного покоя, если геометрическая сумма приложенных к точке сил и
переносной силы инерции равны нулю 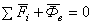 .
.
Тела, падающие на землю, незначительно отклоняются
от вертикали на восток за счет того, что сила инерции Кориолиса направлена на
восток 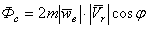 , где
, где 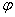 — широта, на которой
находится точка.
— широта, на которой
находится точка.
Тело, брошенное вертикально вверх, отклоняется от
вертикали на запад, т. к. сила инерции Кориолиса в этом случае направлена перпендикулярно
плоскости меридиана к западу.
Состояние покоя механической системы. Состояние покоя механической системы может быть устойчивым,
неустойчивым и безразличным.
Состояние покоя называется устойчивым, если система,
выведенная из положения покоя, совершает малые колебания около этого положения.
Состояние покоя называется неустойчивым, если при
сколь угодно малом отклонении из положения покоя система удаляется от этого
положения.
Состояние называется безразличным, если при
отклонении системы из положения покоя она и в новом положении может оставаться
в состоянии покоя.
Критерий устойчивости состояния покоя
механической системы, устанавливаемый
теоремой Лагранжа — Дирихле.
Те положения покоя консервативной системы, в которых
потенциальная система достигает минимума, являются ее устойчивыми состояниями
покоя 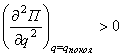 .
.
Вид состояния
покоя механической системы с одной степенью свободы в том случае, если 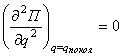 .
.
Если 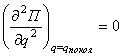 , необходимо вычислить последовательные производные
, необходимо вычислить последовательные производные 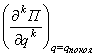 . Если первая не равная нулю производная имеет четный порядок
и при этом положительна, то при
. Если первая не равная нулю производная имеет четный порядок
и при этом положительна, то при 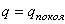 потенциальная энергия
имеет минимум и устойчивое положение.
потенциальная энергия
имеет минимум и устойчивое положение.
Порядок исследования состояния покоя
механической системы на устойчивость.
Выбирается обобщенная координата. Записывается
потенциальная энергия как функция обобщенной координаты. Находится первая и
вторая производные по обобщенным координатам и выясняется, имеет ли
потенциальная энергия в заданном положении минимум.
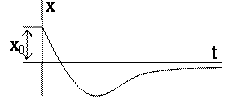
Колебательное движение материальной точки. Восстанавливающая сила (сила упругости)  , сила стремится вернуть точку в равновесное положение,
"с" – коэффициент
жесткости пружины = силе упругости при
деформации, равной единице [Н/м].
, сила стремится вернуть точку в равновесное положение,
"с" – коэффициент
жесткости пружины = силе упругости при
деформации, равной единице [Н/м].
Свободные колебания 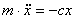 ; обозначив
; обозначив 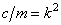 , получаем
, получаем 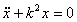 – линейное
однородное диффер-ное уравнение второго порядка, характеристическое
уравнение:
– линейное
однородное диффер-ное уравнение второго порядка, характеристическое
уравнение: 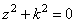 , его корни мнимые, отсюда общее решение дифф-ного уравнения
будет
, его корни мнимые, отсюда общее решение дифф-ного уравнения
будет 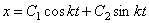 , C1, C2 – постоянные
интегрирования. Для их определения находим уравнение скоростей:
, C1, C2 – постоянные
интегрирования. Для их определения находим уравнение скоростей: 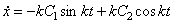 ,
подставляем начальные условия в уравнения для
х и
,
подставляем начальные условия в уравнения для
х и 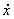 , откуда
, откуда 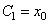 ,
, 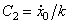 , т.е.
, т.е. 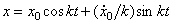 .
.
Можно
обозначить  ,
, 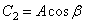 отсюда
отсюда 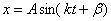 – уравнение
гармонических колебаний.
– уравнение
гармонических колебаний. 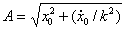 –амплитуда,
–амплитуда, 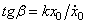 ,
, 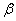 – начальная фаза
свободных колебаний;
– начальная фаза
свободных колебаний; 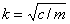 – циклическая
частота (угловая, собственная) колебаний;
период колебаний:
– циклическая
частота (угловая, собственная) колебаний;
период колебаний: 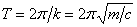 , где k и
Т не зависят от начальных условий – изохронность колебаний; амплитуда и начальная фаза зависят о начальных условий.
Под действием постоянной силы Р происходит смещение
центра колебаний в сторону действия силы Р на величину статического отклонения
, где k и
Т не зависят от начальных условий – изохронность колебаний; амплитуда и начальная фаза зависят о начальных условий.
Под действием постоянной силы Р происходит смещение
центра колебаний в сторону действия силы Р на величину статического отклонения 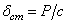 . Если Р – сила тяжести, то
. Если Р – сила тяжести, то 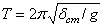 .
.
Затухающие колебания при
действии 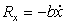 сила
сопротивления, пропорциональная скорости (вязкое трение).
сила
сопротивления, пропорциональная скорости (вязкое трение).
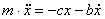 , обозначив
, обозначив 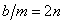 , получаем:
, получаем:
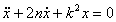 , характеристическое
уравнение:
, характеристическое
уравнение: 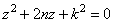 , его
корни:
, его
корни: 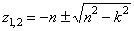 . а) При n<k корни
мнимые, отсюда общее решение дифф.ур-ия имеет вид:
. а) При n<k корни
мнимые, отсюда общее решение дифф.ур-ия имеет вид: 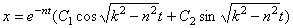 , обозначив
, обозначив  ,
, 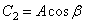 имеем
имеем 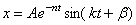 . Множитель
. Множитель 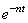 показывает, что колебания затухающие. График заключен между двумя
симметричными относительно оси t кривыми
показывает, что колебания затухающие. График заключен между двумя
симметричными относительно оси t кривыми
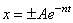 . Из начальных условий:
. Из начальных условий: 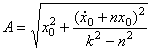 ,
, 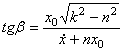 ; частота затухающих колебаний:
; частота затухающих колебаний: 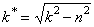 ; период:
; период: 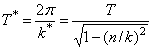 , период затухающих колебаний больше периода свободных
колебаний (при небольших сопротивлениях
, период затухающих колебаний больше периода свободных
колебаний (при небольших сопротивлениях 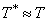 ). Амплитуды колебаний уменьшаются:
). Амплитуды колебаний уменьшаются: 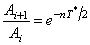 – декремент колебаний;
– декремент колебаний;
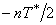 логарифмический
декремент; "n" – коэффициент затухания.
логарифмический
декремент; "n" – коэффициент затухания.
Апериодическое движение точки при 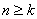 или
или 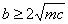 . При
. При 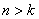 корни
характеристич-ого ур-я вещественны, общее решение:
корни
характеристич-ого ур-я вещественны, общее решение: 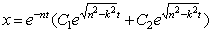 , обозначая
, обозначая 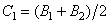 ,
, 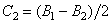 ,
, 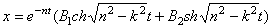 (ch, sh – гиперболические косинус и
синус), если ввести
(ch, sh – гиперболические косинус и
синус), если ввести 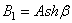 ,
, 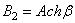 , то
, то 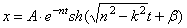 – это уравнение не
колебательного движения (апериодического), т.к. гиперболический синус не
является периодической функцией. При
– это уравнение не
колебательного движения (апериодического), т.к. гиперболический синус не
является периодической функцией. При 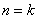 корни характеристич.
ур-я вещественны, равны и отрицательны:
корни характеристич.
ур-я вещественны, равны и отрицательны: 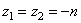 , общее решение:
, общее решение: 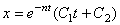 , или
, или 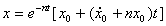 , движение также апериодическое.
, движение также апериодическое.
Вынужденные колебания кроме
восстанавливающей силы действует переменная возмущающая сила, обычно, по
гармоническому закону: 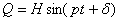 , р – частота возмущающей силы,
, р – частота возмущающей силы, 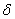 – начальная фаза.
– начальная фаза. 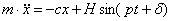 ,
, 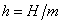 ,
, 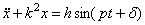 – дифференциальное
уравнение вынужденных колебаний (неоднородное линейное дифф-ное ур-ие). Его
общее решение = сумме общего решения однородного уравнения
– дифференциальное
уравнение вынужденных колебаний (неоднородное линейное дифф-ное ур-ие). Его
общее решение = сумме общего решения однородного уравнения 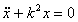 и частного решения данного
уравнения:
и частного решения данного
уравнения: 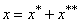 , где
, где 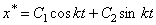 ,
, 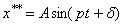 – частное решение
ищется в виде подобном правой части уравнения. Подставляя решение в уравнение,
находим
– частное решение
ищется в виде подобном правой части уравнения. Подставляя решение в уравнение,
находим 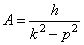 ,
, 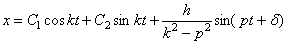 . Величина
статического отклонения:
. Величина
статического отклонения: 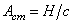 ,
, 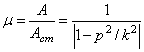 – коэфф-нт
динамичности, во сколько раз амплитуда колебаний превосходит статическое
отклонение.
– коэфф-нт
динамичности, во сколько раз амплитуда колебаний превосходит статическое
отклонение.
Вынужденные колебания малой частоты и колебания большой частоты.
Вынужденные колебания, частота p которых меньше
частоты k свободных колебаний,
называются вынужденными колебаниями малой частоты. Фаза вынужденных колебаний
большой частоты 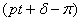 отличается от фазы
возмущающей силы
отличается от фазы
возмущающей силы 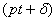 на величину
на величину 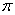 , т. е. фазы вынужденных колебаний и возмущающей силы
противоположны.
, т. е. фазы вынужденных колебаний и возмущающей силы
противоположны.
При 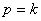
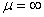 – явление
резонанса (частота возмущающей силы равна частоте собственных
колебаний, при этом амплитуда неограниченно возрастает). При
– явление
резонанса (частота возмущающей силы равна частоте собственных
колебаний, при этом амплитуда неограниченно возрастает). При
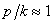 наступает явление,
называемое биениями:
наступает явление,
называемое биениями: 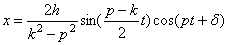 . Обозначая
. Обозначая 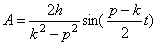 , получаем
, получаем 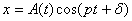 – происходит наложение дополнительных колебаний, вызванных
возмущающей силой, на собственно вынужденные колебания – колебания частоты р, амплитуда которых является периодической функцией.
– происходит наложение дополнительных колебаний, вызванных
возмущающей силой, на собственно вынужденные колебания – колебания частоты р, амплитуда которых является периодической функцией.
Явление
резонанса возникает при совпадении частот вынужденных и свободных кол-ний точки
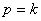 . Диф-ное ур-ние:
. Диф-ное ур-ние: 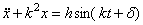 . Частное решение:
. Частное решение: 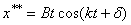 ,
, 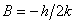 , т.е. общее решение
диф-ного ур-ния:
, т.е. общее решение
диф-ного ур-ния: 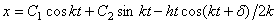 .
Ур-ние показывает, что амплитуда вынужденных колебаний при резонансе возрастает
пропорционально времени. Период
.
Ур-ние показывает, что амплитуда вынужденных колебаний при резонансе возрастает
пропорционально времени. Период 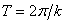 , фаза
вынужденных колебаний отстает от фазы возмущающей силы на
, фаза
вынужденных колебаний отстает от фазы возмущающей силы на
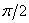 .
.
Коэффициент динамичности и график его зависимости от отношения p/k.
Отношение 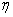 амплитуды вынужденных колебаний A к статическому смещению A0 называется коэффициентом
динамичности
амплитуды вынужденных колебаний A к статическому смещению A0 называется коэффициентом
динамичности
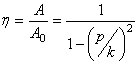 .
.
График зависимости показывает, что при увеличении
частоты возмущающей силы от p = 0 до p = k коэффициент
динамичности растет от единицы до бесконечности, а при дальнейшем увеличении p до бесконечности коэффициент
динамичности убывает от бесконечности до нуля.
Вынужденные колебания при наличии вязкого трения: 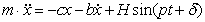 ,
, 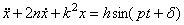 , общее решение в зависимости от величины k
и n:
, общее решение в зависимости от величины k
и n:
1) при n<k 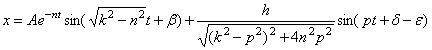 ;
;
2) при n>k 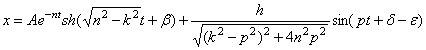 ;
;
3) при n=k 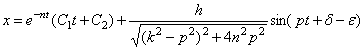 .
.
Общие теоремы динамики точки. Теорема об изменении
количества движения материальной точки. Теорема об изменении момента количества
движения материальной точки. Работа силы. Мощность. Теорема об изменении
кинетической энергии точки. Потенциальная энергия
Теорема об изменении количества движения матер.
точки.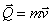 – количество
движения материальной точки,
– количество
движения материальной точки, 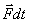 – элементарный импульс
силы.
– элементарный импульс
силы. 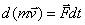 – элементарное
изменение количества движения материальной точки равно элементарному импульсу
силы, приложенной к этой точке (теорема в дифференц-ной форме) или
– элементарное
изменение количества движения материальной точки равно элементарному импульсу
силы, приложенной к этой точке (теорема в дифференц-ной форме) или 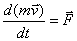 – производная по времени от количества движения материальной
точки равна равнодействующей сил, приложенных к этой точке. Проинтегрируем:
– производная по времени от количества движения материальной
точки равна равнодействующей сил, приложенных к этой точке. Проинтегрируем: 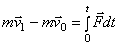 – изменение количества движения материальной
точки за конечный промежуток времени равно элементарному импульсу силы,
приложенной к этой точке, за тот же промежуток времени.
– изменение количества движения материальной
точки за конечный промежуток времени равно элементарному импульсу силы,
приложенной к этой точке, за тот же промежуток времени.
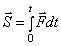 – импульс силы за промежуток времени [0,t]. В проекциях на оси координат:
– импульс силы за промежуток времени [0,t]. В проекциях на оси координат: 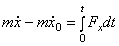 и т.д.
и т.д.
Теорема об изменении момента количества движения матер. точки. 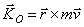 - момент количества движения матер. точки относительно
центра О.
- момент количества движения матер. точки относительно
центра О. 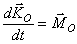 – производная по времени от момента количества
движения матер. точки относительно какого-либо центра равна моменту силы,
приложенной к точке, относительно того же центра. Проектируя векторное
равенство на оси координат. получаем
три скалярных уравнения:
– производная по времени от момента количества
движения матер. точки относительно какого-либо центра равна моменту силы,
приложенной к точке, относительно того же центра. Проектируя векторное
равенство на оси координат. получаем
три скалярных уравнения: 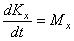 и т.д. - производная от момента кол-ва
движения матер. точки относительно какой-либо оси равна моменту силы,
приложенной к точке, относительно той же оси. При действии центральной силы,
проходящей через О, МО= 0, отсюда
и т.д. - производная от момента кол-ва
движения матер. точки относительно какой-либо оси равна моменту силы,
приложенной к точке, относительно той же оси. При действии центральной силы,
проходящей через О, МО= 0, отсюда 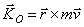 =const.
=const. 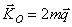 =const, где
=const, где 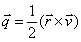 – секторная скорость. Под действием центральной силы точка движется по
плоской кривой с постоянной секторной скоростью, т.е. радиус-вектор точки
описывает ("ометает") равные площади в любые равные промежутки
времени (закон площадей) Этот закон имеет место при движении планет и
спутников – один из законов Кеплера.
– секторная скорость. Под действием центральной силы точка движется по
плоской кривой с постоянной секторной скоростью, т.е. радиус-вектор точки
описывает ("ометает") равные площади в любые равные промежутки
времени (закон площадей) Этот закон имеет место при движении планет и
спутников – один из законов Кеплера.
Работа силы. Элементарная
работа 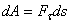 ,
, 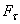 – проекция силы на
касательную к траектории, направленная в сторону перемещения, или
– проекция силы на
касательную к траектории, направленная в сторону перемещения, или 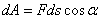 .
.
Если 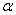 – острый, то dA>0,
тупой – <0, a=90o: dA=0.
– острый, то dA>0,
тупой – <0, a=90o: dA=0. 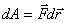 – скалярное
произведение вектора силы на вектор элементарного перемещения точки ее
приложения;
– скалярное
произведение вектора силы на вектор элементарного перемещения точки ее
приложения; 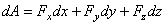 – аналитическое
выражение элементарной работы силы.
Работа силы на любом конечном перемещении М0М1:
– аналитическое
выражение элементарной работы силы.
Работа силы на любом конечном перемещении М0М1: 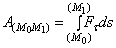 . Если сила
постоянна, то
. Если сила
постоянна, то 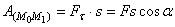 . Единицы работы:[1 Дж (джоуль) = 1 Нм].
. Единицы работы:[1 Дж (джоуль) = 1 Нм].
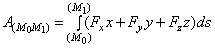 , т.к.
, т.к. 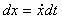 и
т.д., то
и
т.д., то 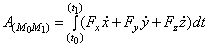 .
.
Теорема о работе силы: Работа
равнодействующей силы равна алгебраической сумме работ составляющих сил на том
же перемещении 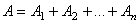 .
.
Работа силы тяжести: 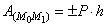 , >0, если начальная точка выше конечной.
, >0, если начальная точка выше конечной.
Работа силы упругости: 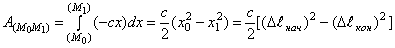 – работа силы
упругости равна половине произведения коэффициента жесткости на разность
квадратов начального и конечного удлинений (или сжатий) пружины.
– работа силы
упругости равна половине произведения коэффициента жесткости на разность
квадратов начального и конечного удлинений (или сжатий) пружины.
Работа силы трения: если сила
трения const, то 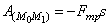 - всегда отрицательна,
- всегда отрицательна,
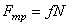 , f – коэфф.трения, N – нормальная реакция поверхности.
, f – коэфф.трения, N – нормальная реакция поверхности.
Работа силы тяготения. Сила
притяжения (тяготения): 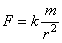 , из
, из 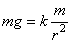 , находим коэфф.
, находим коэфф. 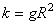 .
. 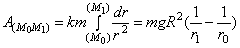 – не зависит от
траектории.
– не зависит от
траектории.
Мощность – величина,
определяющая работу в единицу времени, 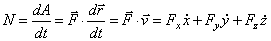 . Если изменение работы происходит равномерно, то мощность
постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) = 1000 Вт, 1л.с. (лошадиная сила) = 75 кгс×м/с = 736 Вт].
. Если изменение работы происходит равномерно, то мощность
постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) = 1000 Вт, 1л.с. (лошадиная сила) = 75 кгс×м/с = 736 Вт].
Теорема об изменении кинетической энергии точки. В дифференциальной форме: 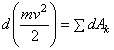 – полный дифференциал кинетической энергии мат.точки = элементарной работе всех действующих на точку сил.
– полный дифференциал кинетической энергии мат.точки = элементарной работе всех действующих на точку сил. 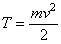 – кинетическая
энергия материальной точки. В конечном
виде:
– кинетическая
энергия материальной точки. В конечном
виде: 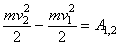 – изменение
кинетической энергии мат. точки, при переходе ее из начального
в конечное (текущее) положение равно сумме работ на этом перемещении всех сил,
приложенных к точке.
– изменение
кинетической энергии мат. точки, при переходе ее из начального
в конечное (текущее) положение равно сумме работ на этом перемещении всех сил,
приложенных к точке.
Силовое поле – область, в
каждой точке которой на помещенную в ней материальную точку действует сила,
однозначно определенная по величине и направлению в любой момент времени, т.е.
должно быть известна 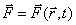 . Нестационарное силовое поле, если
. Нестационарное силовое поле, если 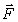 явно зависит от t, стационарное
силовое поле, если сила не зависит от
времени. Рассматриваются стационарные силовые поля, когда сила зависит только
от положения точки:
явно зависит от t, стационарное
силовое поле, если сила не зависит от
времени. Рассматриваются стационарные силовые поля, когда сила зависит только
от положения точки: 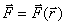 и
и 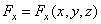 и т.д.
и т.д.
Свойства стационарных силовых полей:
Работа сил стац. поля зависит в общем случае от
начального М1 и конечного М2 положений и траектории, но
не зависит от закона движения матер. точки.
Имеет место равенство А2,1= – А1,2. Для нестационарных
полей эти свойства на выполняются.
Примеры: поле силы тяжести, электростатическое поле,
поле силы упругости.
Стационарные
силовые поля, работа сил которых не зависит от траектории (пути) движения матер. точки и определяется только ее начальным
и конечным положениями назыв. потенциальными
(консервативными). 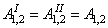 , где I и II – любые пути,
, где I и II – любые пути, 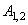 – общее значение
работы. В потенциальных силовых полях существует такая функция, однозначно
зависящая от координат точек системы, через которую проекции силы на
координатные оси в каждой точке поля выражаются так:
– общее значение
работы. В потенциальных силовых полях существует такая функция, однозначно
зависящая от координат точек системы, через которую проекции силы на
координатные оси в каждой точке поля выражаются так:
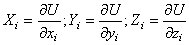 . Функция U=U(x1,y1,z1,x2,y2,z2,…xn,yn,zn)
назыв. силовой функцией. Элементарная работа сил поля:
. Функция U=U(x1,y1,z1,x2,y2,z2,…xn,yn,zn)
назыв. силовой функцией. Элементарная работа сил поля: 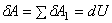 . Если силовое поле является потенц-ным, элементарная работа
сил в этом поле равна полному дифференциалу силовой функции. Работа
сил на конечном перемещении
. Если силовое поле является потенц-ным, элементарная работа
сил в этом поле равна полному дифференциалу силовой функции. Работа
сил на конечном перемещении 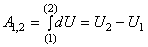 , т.е. работа сил в потенц-ном поле равна разности значений
силовой функции в конечном и начальном положениях и не зависит о формы траектории. На замкнутом
перемещении работа равна 0.
, т.е. работа сил в потенц-ном поле равна разности значений
силовой функции в конечном и начальном положениях и не зависит о формы траектории. На замкнутом
перемещении работа равна 0.
Потенциальная энергия П равна сумме работ
сил потенциального поля на перемещении системы из данного положения в нулевое.
В нулевом положении П0=
0. П=П(x1,y1,z1,x2,y2,z2,…xn,yn,zn). Работа сил поля на перемещении системы из 1-го
положения во 2-ое равна разности потенциальных энергий 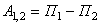 .
.
Эквипотенциальные поверхности –
поверхности равного потенциала. Сила направлена по нормали к эквипотенциальной
поверхности. Потенциальная энергия системы отличается от силовой функции,
взятой со знаком минус, на постоянную величину U0: А1,0= П =U0 – U. Потенциальная энергия поля силы тяжести: 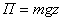 .
.
Центральная сила – сила,
которая в любой точке пространства направлена по прямой, проходящей через некоторую точку (центр), и модуль
ее зависит только от расстояния r точки
массой m до центра: 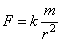 ,
, 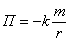 . Центральной является гравитационная сила
. Центральной является гравитационная сила 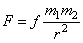 ,
,
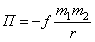 , f
= 6,67×10-11м3/(кгс2) – постоянная тяготения.
, f
= 6,67×10-11м3/(кгс2) – постоянная тяготения.
Первая космическая скорость v1=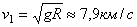 , R =
6,37×106м –
радиус Земли; тело выходит на круговую орбиту.
, R =
6,37×106м –
радиус Земли; тело выходит на круговую орбиту.
Вторая космическая скорость: 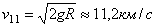 , траектория тела парабола, при
, траектория тела парабола, при 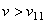 – гипербола.
– гипербола.
Потенц. энергия восстанавливающей силы пружин: 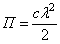 , где
, где 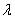 – модуль приращения
длины пружины. Работа восстанавливающей силы пружины:
– модуль приращения
длины пружины. Работа восстанавливающей силы пружины: 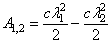 , где
, где 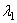 и
и 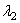 – деформации,
соответствующие начальной и конечной точкам пути.
– деформации,
соответствующие начальной и конечной точкам пути.
Динамика материальной системы. Центр масс. Геометрия масс.
Теорема о движении центра масс системы. Теорема об изменении количества
движения системы. Теорема об
изменении момента количеств движения системы.
Материальная система –
совокупность материальных точек, движение которых взаимосвязаны.
Масса системы = сумме масс всех точек (или тел), образующих систему: 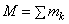 .
.
Центр масс (центр инерции) –
геометрическая точка, радиус-вектор 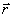 которой определяется
равенством:
которой определяется
равенством: 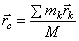 , где
, где 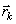 – радиусы-векторы точек, образующих
систему. Координаты центра масс:
– радиусы-векторы точек, образующих
систему. Координаты центра масс: 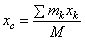 и т.д.
и т.д.
Внешние силы Fe – силы,
действующие на точки системы со стороны тел, не входящих в систему.
Внутренние силы Fi
– силы, вызванные взаимодействием точек, входящих в систему. Свойства внутренних сил: 1) Геометрическая сумма (главный вектор) всех
внутренних сил = 0; 2) Геометрическая сумма моментов всех внутренних сил
относительно произвольной точки = 0.
Дифф-ные ур-ния движения системы матер.точек: 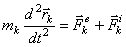 или в проекциях на оси
координат:
или в проекциях на оси
координат: 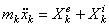 и т.д. для каждой
точки (тела) системы.
и т.д. для каждой
точки (тела) системы.
Момент инерции матер.точки относительно некоторой оси называется произведение
массы m этой точки
на квадрат ее расстояния h до оси: mh2.
Момент инерции тела (системы)
относительно оси Оz: 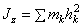 . При непрерывном распределении масс (тело) сумма переходит в
интеграл:
. При непрерывном распределении масс (тело) сумма переходит в
интеграл: 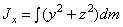 ,
, 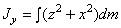 ,
, 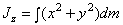 – относительно
координатных осей.
– относительно
координатных осей. 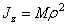 , где
, где 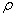 – радиус инерции тела – расстояние от оси до точки в которой нужно
сосредоточить всего тела, чтобы ее момент инерции равнялся моменту инерции
тела. Момент инерции относительно оси (осевой момент инерции) всегда >0.
– радиус инерции тела – расстояние от оси до точки в которой нужно
сосредоточить всего тела, чтобы ее момент инерции равнялся моменту инерции
тела. Момент инерции относительно оси (осевой момент инерции) всегда >0.
Полярный момент инерции 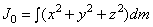 ;
; 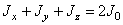 .
.
Центробежный момент инерции Jxy для матер.точки называется произведение ее
координат x
и y на ее массу
m. Для тела центробежными моментами инерции
называются величины, определяемые равенствами: 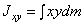 ;
; 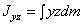 ;
; 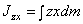 . Центробежные моменты инерции симметричны
относительно своих индексов, т.е.
. Центробежные моменты инерции симметричны
относительно своих индексов, т.е. 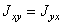 и т.д. В отличие от осевых, центробежные моменты инерции могут иметь любой знак
и обращаться в нуль.
и т.д. В отличие от осевых, центробежные моменты инерции могут иметь любой знак
и обращаться в нуль.
Главной осью инерции тела
назыв. ось, для которой оба центробежных момента инерции, содержащие индекс
этой оси, равны нулю. Например, если 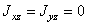 , то
ось z – главная ось инерции.
, то
ось z – главная ось инерции.
Главной центральной осью инерции назыв. главная ось инерции, проходящая через центр
масс тела. 1) Если тело имеет плоскость симметрии, то любая ось,
перпендикулярная к этой плоскости, будет главной осью инерции тела для точки, в
которой ось пересекает плоскость. 2) Если тело имеет ось симметрии, то эта ось
является главной осью инерции тела (ось динамической симметрии). Размерность всех моментов инерции [кгм2]
Центробежный
момент инерции зависят не только от направления координатных осей, но и от выбора
начала координат.
Тензор инерции в данной точке: 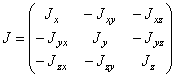
Моменты инерции некоторых однородных тел:
стержень массы
m и длины L: 
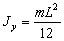 ;
; 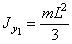 .
.
Однородный сплошной диск с центром в точке С радиуса R и массы m: 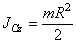 .
.
Полый цилиндр: 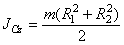 ,
,
Цилиндр с массой распределенной по ободу (обруч): 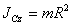 .
.
Теорема Гюйгенса-Штейнера
момент инерции тела относительно произвольной оси равен моменту инерции
относительно оси ей параллельной и проходящей через центр масс тела плюс
произведение массы тела на квадрат расстояния между осями:
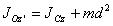 . Наименьший момент инерции будет относительно той оси, которая
проходит через центр масс.
. Наименьший момент инерции будет относительно той оси, которая
проходит через центр масс.
Момент инерции относительно произвольной оси L:
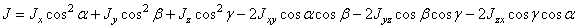 , если координатные оси являются главными относительно своего
начала, то:
, если координатные оси являются главными относительно своего
начала, то: 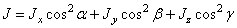 .
.
Теорема о движении центра масс системы. Произведение массы системы на ускорение ее центра масс равно
геометрической сумме всех действующих на систему внешних сил 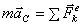 – дифференциальное уравнение движения центра
масс. В проекциях на оси координат:
– дифференциальное уравнение движения центра
масс. В проекциях на оси координат: 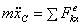 .
.
Закон сохранения движения центра масс. Если главный вектор (векторная сумма) внешних сил остается все время
равным нулю, то центр масс механической системы находится в покое или движется
прямолинейно и равномерно. Аналогично в проекциях на оси, если 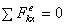 Þ
Þ 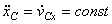 , если при этом в начальный момент
, если при этом в начальный момент 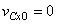 , то тогда
, то тогда 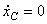 и
и 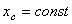 .
.
Количество движения системы Q (иногда обозначают К) – вектор, равный
геометрической сумме (главному вектору) количеств движения
всех точек системы:
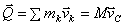 , где М – масса всей системы,
, где М – масса всей системы, 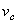 – скорость центра
масс.
– скорость центра
масс.
Теорема об изменении количества движения системы: 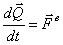 – производная по
времени от количества движения механической системы геометрически равна
главному вектору внешних сил, действующих на эту систему. В проекциях:
– производная по
времени от количества движения механической системы геометрически равна
главному вектору внешних сил, действующих на эту систему. В проекциях: 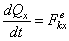 , и т.д. Теорема об изменении кол-ва движения системы в интегральной
форме:
, и т.д. Теорема об изменении кол-ва движения системы в интегральной
форме:
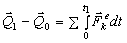 , где
, где 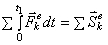 – импульсы внешних сил.
– импульсы внешних сил.
В проекциях: 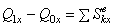 и т.д. количество
движения системы за некоторый промежуток времени равно сумме импульсов
действующих на систему внешних сил за тот же промежуток времени.
и т.д. количество
движения системы за некоторый промежуток времени равно сумме импульсов
действующих на систему внешних сил за тот же промежуток времени.
Закон сохранения количества движения – если сумма всех внешних сил, действующих на систему, = 0, то вектор
количества движения системы будет постоянен по модулю и направлению: 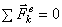 тогда
тогда  , аналогично в проекциях:
, аналогично в проекциях: 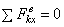 тогда
тогда 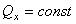 . Из закона следует, что внутренние силы изменить суммарное
количество движение системы не могут.
. Из закона следует, что внутренние силы изменить суммарное
количество движение системы не могут.
Тело переменной массы, масса
которого непрерывно изменяется с течением времени 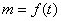 (пр.: ракета, топливо
которой убывает). Дифф-ное уравнение движения точки переменной массы:
(пр.: ракета, топливо
которой убывает). Дифф-ное уравнение движения точки переменной массы:
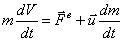 – уравнение Мещерского, u –
относительная скорость отделяющихся частиц.
– уравнение Мещерского, u –
относительная скорость отделяющихся частиц. 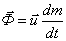 – реактивная сила,
– реактивная сила, 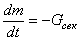 — секундный расход
топлива,
— секундный расход
топлива, 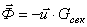 . Реактивная сила направлена в противоположную сторону
относительной скорости истечения топлива.
. Реактивная сила направлена в противоположную сторону
относительной скорости истечения топлива.
Формула Циолковского: 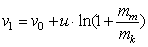 — определяет скорость
ракеты, когда все топливо будет израсходовано – скорость в конце активного
участка,
— определяет скорость
ракеты, когда все топливо будет израсходовано – скорость в конце активного
участка, 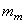 – масса топлива,
– масса топлива, 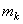 – масса корпуса ракеты,
– масса корпуса ракеты, 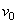 – начальная скорость.
– начальная скорость. 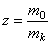 – число Циолковского,
– число Циолковского, 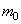 – стартовая масса
ракеты. От режима работы ракетного двигателя, т.е. от того насколько быстро
сжигается топливо, скорость ракеты в конце периода горения не зависит. Для достижения 1-ой космической скорости 7,9 км/с, при
– стартовая масса
ракеты. От режима работы ракетного двигателя, т.е. от того насколько быстро
сжигается топливо, скорость ракеты в конце периода горения не зависит. Для достижения 1-ой космической скорости 7,9 км/с, при 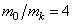 , скорость отброса должна быть 6 км/с, что трудно
осуществить, поэтому применяются составные (многоступенчатые) ракеты.
, скорость отброса должна быть 6 км/с, что трудно
осуществить, поэтому применяются составные (многоступенчатые) ракеты.
Главный момент количеств движения матер. системы (кинетический момент) 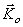 – величина, равная геометрической сумме моментов количеств
движения всех точек системы относительно центра О.
– величина, равная геометрической сумме моментов количеств
движения всех точек системы относительно центра О. 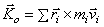 .
.
Теорема об изменении момента количеств движения
системы (теорема об изменении кинетического момента):
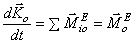 — производная по
времени от кинетического момента механич. системы относительно некоторого неподвижного
центра геометрически равна главному моменту внешних сил, действующих на эту
систему относительно того же центра. Аналогичные равенства относительно осей
координат:
— производная по
времени от кинетического момента механич. системы относительно некоторого неподвижного
центра геометрически равна главному моменту внешних сил, действующих на эту
систему относительно того же центра. Аналогичные равенства относительно осей
координат: 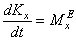 и т.д.
и т.д.
Закон сохранения кинетического момента: если 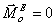 , то
, то 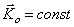 . Главный момент количеств движения
системы является характеристикой вращательного движения. Кинетический момент
вращающегося тела относительно оси вращения равен произведению момента инерции
тела относительно этой оси на угловую скорость тела:
. Главный момент количеств движения
системы является характеристикой вращательного движения. Кинетический момент
вращающегося тела относительно оси вращения равен произведению момента инерции
тела относительно этой оси на угловую скорость тела: 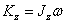 . Если
. Если 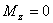 , то
, то 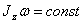 ,
, 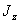 – момент инерции тела.
– момент инерции тела.
Теорема об изменении кинетической энергии системы. Динамика
твердого тела. Дифференциальные уравнения поступательного движения тела.
Дифференциальные уравнения вращения тела вокруг неподвижной оси. Динамика
плоского движения тела. Принцип Даламбера (метод кинетостатики). Определение
реакций при вращении тела вокруг неподвижной оси.
Кинетическая энергия системы –
скалярная величина Т, равная
арифметической сумме кинетической энергий всех точек системы: 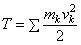 . Если система состоит из нескольких тел, то
. Если система состоит из нескольких тел, то 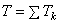 . Поступательное движение:
. Поступательное движение: 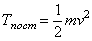 . Вращательное движ-ие:
. Вращательное движ-ие: 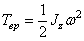 , где
, где 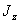 – момент инерции
относительно оси вращения. Плоскопараллельное (плоское) движ-ие: Тпл=
– момент инерции
относительно оси вращения. Плоскопараллельное (плоское) движ-ие: Тпл=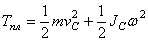 , где
, где
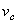 – скорость центра масс. Общий случай:
– скорость центра масс. Общий случай: 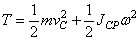 , где
, где 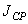 – момент инерции тела
относительно мгновенной оси.
– момент инерции тела
относительно мгновенной оси.
Теорема Кенига: 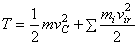 – кинетич. энергия мех. сист. = сумме кинетич. энергии
центра масс системы, масса которого равна массе всей системы, и кинетич.
энергии этой системы в ее относительном движении относительно центра масс.
– кинетич. энергия мех. сист. = сумме кинетич. энергии
центра масс системы, масса которого равна массе всей системы, и кинетич.
энергии этой системы в ее относительном движении относительно центра масс.
Работа
силы: 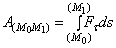 , работа
момента:
, работа
момента: 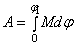 . Мощность: N= Fv,
N=Mzw.
. Мощность: N= Fv,
N=Mzw.
Теорема об изменении кинетической энергии системы: в дифференциальной форме: 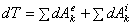 , где
, где 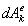 ,
, 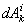 – элементарные работы,
действующих на точку внешних и внутренних сил, в конечной форме:
– элементарные работы,
действующих на точку внешних и внутренних сил, в конечной форме: 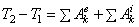 . Для неизменяемой системы
. Для неизменяемой системы  и
и 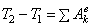 , т.е. изменение кинетической энергии твердого тела на
некотором перемещении равно сумме работ внешних сил, действующих на тело на этом
перемещении. Если сумма работ реакций связей на любом возможном перемещении
системы равна нулю, то такие связи называются идеальными.
, т.е. изменение кинетической энергии твердого тела на
некотором перемещении равно сумме работ внешних сил, действующих на тело на этом
перемещении. Если сумма работ реакций связей на любом возможном перемещении
системы равна нулю, то такие связи называются идеальными.
Коэффициент полезного действия (кпд): 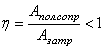 , Апол.сопр. – работа
полезных сил сопротивления (сил, для которых предназначена машина), Азатр=
Апол.сопр.+ Авр.сопр. –
затраченная работа, Авр.сопр.– работа вредных сил сопротивления
(силы трения, сопротивления воздуха и т.п.).
, Апол.сопр. – работа
полезных сил сопротивления (сил, для которых предназначена машина), Азатр=
Апол.сопр.+ Авр.сопр. –
затраченная работа, Авр.сопр.– работа вредных сил сопротивления
(силы трения, сопротивления воздуха и т.п.).
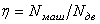 , где Nмаш – полезная мощность машины, Nдв
– мощность дв-ля, приводящего ее в движение.
, где Nмаш – полезная мощность машины, Nдв
– мощность дв-ля, приводящего ее в движение.
Закон сохранения полной механической энергии: Т + П = const. Если система движется под действием потенциальных
сил, то сумма кинетической и потенциальной энергий сохраняет постоянное
значение. (Т + П — интеграл энергии). Потенциальные силы – силы, работа которых не зависит от вида
траектории, по которой перемещается точка (пр.: сила тяжести, сила упругости).
Непотенциальные – напр.: силы трения.
Механическая энергия – сумма
кинетической и потенциальной энергий. Расход механической энергии обычно
означает превращение ее в теплоту, электричество, звук или свет, а приток
механической энергии связан с обратным процессом превращения различных видов
энергии в механическую энергию.
Динамика твердого тела
Абсолютно твердое тело как система
материальных точек - неизменяемая система бесконечно большого числа
элементарных частиц, бесконечно малое расстояние между
которыми всегда неизменно.
Масса твердого тела как системы материальных точек - предельное
значение суммы масс ее элементарных частиц: 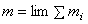 .
.
Дифференциальные ур-ния поступательного движения твердого тела: 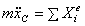 и т.д.
и т.д. 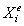 – проекция внешней силы. Все точки тела движутся так же, как и
его центр масс С. Для осуществления поступательного движения необходимо, чтобы
главный момент всех внешних сил относительно центра масс был равен 0:
– проекция внешней силы. Все точки тела движутся так же, как и
его центр масс С. Для осуществления поступательного движения необходимо, чтобы
главный момент всех внешних сил относительно центра масс был равен 0: 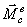 =0.
=0.
Дифф-ные ур-ния вращения твердого тела вокруг неподвижной оси: 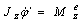 , где Jz – момент инерции тела относительно оси вращения z,
, где Jz – момент инерции тела относительно оси вращения z, 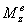 – момент
внешних сил относительно оси вращения (вращающий момент).
– момент
внешних сил относительно оси вращения (вращающий момент). 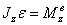 , где
, где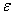 – угловое ускорение,
чем больше момент инерции при данном
– угловое ускорение,
чем больше момент инерции при данном 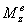 , тем меньше ускорение, т.е
момент инерции при вращательном движении является аналогом массы при
поступательном. Зная
, тем меньше ускорение, т.е
момент инерции при вращательном движении является аналогом массы при
поступательном. Зная 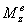 , можно найти закон вращения тела
, можно найти закон вращения тела 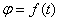 , и, наоборот, зная
, и, наоборот, зная 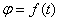 , можно найти момент. Частные случаи: 1)
если
, можно найти момент. Частные случаи: 1)
если 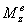 = 0, то
= 0, то 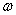 = const – тело вращается равномерно; 2)
= const – тело вращается равномерно; 2) 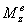 = const, то
= const, то 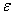 = const – вращение
равнопеременное. Уравнение аналогичное дифф-ному уравнению
прямолинейного движения точки
= const – вращение
равнопеременное. Уравнение аналогичное дифф-ному уравнению
прямолинейного движения точки 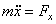 .
.
Физический маятник – твердое
тело, совершающее колебания вокруг неподвижной горизонтальной оси под действием
силы тяжести.
Ур-ние
вращательного движения: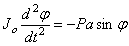 , обозначая
, обозначая 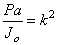 , получаем дифф-ное уравнение колебаний маятника:
, получаем дифф-ное уравнение колебаний маятника: 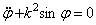 , где k – частота колебаний маятника. Рассматривая малые
колебания, можно считать
, где k – частота колебаний маятника. Рассматривая малые
колебания, можно считать 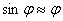 , тогда
, тогда 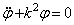 – дифф-ное уравнение
гармонических колебаний. Решение этого уравнения:
– дифф-ное уравнение
гармонических колебаний. Решение этого уравнения: 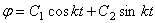 или
или 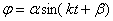 , где
, где 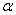 – амплитуда колебаний
маятника,
– амплитуда колебаний
маятника, 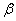 – начальная фаза
колебаний. Период малых колебаний физического маятника
– начальная фаза
колебаний. Период малых колебаний физического маятника 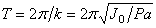 . Для малых колебаний маятника период не зависит от угла
начального отклонения, этот результат является приближенным.
. Для малых колебаний маятника период не зависит от угла
начального отклонения, этот результат является приближенным.
Для математического
маятника (материальной точки,
подвешенной на нерастяжимой нити и движущейся под действием силы тяжести) имеем
дифф. уравнения движения:
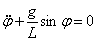 , где L – длина нити. Если
, где L – длина нити. Если 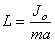 , то
математический маятник будет двигаться так же, как и физический (период
колебаний совпадает). Величина L назыв-ся приведенной длиной физического маятника. Точка К, отстоящая от оси подвеса на расстоянии
ОК=L, назыв-ся центром качаний физич. маятника.
Если ось подвеса взять в точке К, то точка О будет
центром качаний и наоборот – свойство
взаимности. Расстояние ОК всегда
>ОС, т.е. центр качаний всегда расположен ниже центра масс.
, то
математический маятник будет двигаться так же, как и физический (период
колебаний совпадает). Величина L назыв-ся приведенной длиной физического маятника. Точка К, отстоящая от оси подвеса на расстоянии
ОК=L, назыв-ся центром качаний физич. маятника.
Если ось подвеса взять в точке К, то точка О будет
центром качаний и наоборот – свойство
взаимности. Расстояние ОК всегда
>ОС, т.е. центр качаний всегда расположен ниже центра масс.
Динамика плоского движения твердого тела
Положение
тела определяется положением полюса и углом поворота тела вокруг полюса.
Дифф-ные уравнения плоского движения тв. тела:
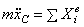 ;
; 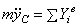 ;
; 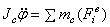 , где С
– центр масс тела, JC – момент инерции тела относительно оси, перпендикулярной
плоскости движения тела и проходящей через его центр масс.
, где С
– центр масс тела, JC – момент инерции тела относительно оси, перпендикулярной
плоскости движения тела и проходящей через его центр масс.
Принцип Даламбера (метод кинетостатики)
В каждый момент движения сумма активных сил, реакций
связей и сил инерции равна нулю 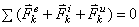 — принцип Даламбера для материальной точки.
— принцип Даламбера для материальной точки.
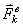 – внешняя сила,
– внешняя сила, 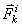 – внутренняя сила.
Сила инерции:
– внутренняя сила.
Сила инерции: 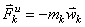 , знак (–) показывает, что сила
инерции направлена в противоположную сторону ускорению.
, знак (–) показывает, что сила
инерции направлена в противоположную сторону ускорению.
Для
системы добавляется уравнение моментов: 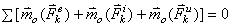 .
.
Обозначают: 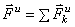 – главный вектор сил инерции,
– главный вектор сил инерции, 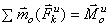 – главный момент сил инерции. Учитывая, что геометрическая сумма внутренних сил и
сумма их моментов равна нулю
– главный момент сил инерции. Учитывая, что геометрическая сумма внутренних сил и
сумма их моментов равна нулю 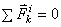 ,
, 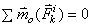 , получаем:
, получаем: 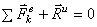 ,
, 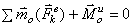 — уравнения
кинетостатики. Принцип Даламбера для системы – если в любой момент времени к
каждой точке системы приложить, кроме реально действующих сил, соответствующие
силы инерции, то полученная система сил будет находиться в равновесии и к ней можно
применять уравнения статики. Это упрощает процесс решения задач.
— уравнения
кинетостатики. Принцип Даламбера для системы – если в любой момент времени к
каждой точке системы приложить, кроме реально действующих сил, соответствующие
силы инерции, то полученная система сил будет находиться в равновесии и к ней можно
применять уравнения статики. Это упрощает процесс решения задач.
Главный вектор сил инерции 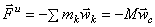 равен произведению
массы тела на ускорение его центра масс и направлен противоположно этому
ускорению.
равен произведению
массы тела на ускорение его центра масс и направлен противоположно этому
ускорению.
Главный момент сил инерции зависит
от вида движения: при поступательном движении 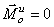 ; при плоском
; при плоском 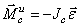 , при вращении вокруг оси z, проходящей через центр масс тела,
, при вращении вокруг оси z, проходящей через центр масс тела, 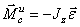 .
.
Определение реакций при вращении твердого тела вокруг неподвижной оси.
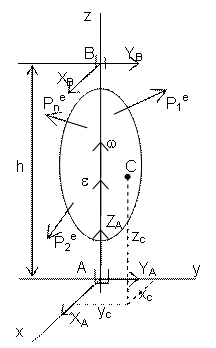 При
вращении тела вокруг неподвижной оси возникают динамические давления на опоры.
Их определение удобно решать методом кинетостатики. Прикладываем силы инерции
для каждой точки: центробежная
При
вращении тела вокруг неподвижной оси возникают динамические давления на опоры.
Их определение удобно решать методом кинетостатики. Прикладываем силы инерции
для каждой точки: центробежная 
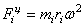 , вращательная
, вращательная 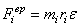 , где
, где 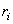 – расстояние от точки до оси вращения.
Проектируя сумму этих сил на оси и учитывая, что
– расстояние от точки до оси вращения.
Проектируя сумму этих сил на оси и учитывая, что 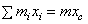 и
и 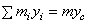 , С – центр масс, получаем проекции главного вектора сил инерции:
, С – центр масс, получаем проекции главного вектора сил инерции:
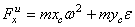 ,
, 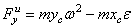 .
.
Проекции главного момента сил инерции = сумме
моментов центробежных и вращательных сил инерций относительно осей координат:
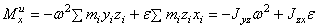 ,
,
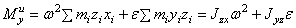 ,
,
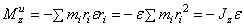 ,
,
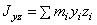 ,
, 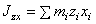 – центробежные моменты инерции,
– центробежные моменты инерции, 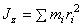
Учитывая внешние силы, можно записать уравнения
равновесия кинетостатики:
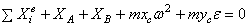 ,
,
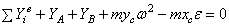 ,
,
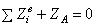 ,
,
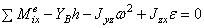 ,
,
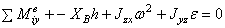 ,
,
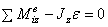 .
.
Последнее уравнение не содержит реакций опор и
представляет собой дифференциальное уравнение вращения тела. Остальные пять
уравнений позволяют определить пять неизвестных реакций. Динамические
составляющие реакций определяются слагаемыми, которые зависят от сил инерции.
Условия отсутствия динамических
составляющих:
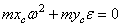 ,
, 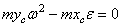 ,
, 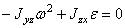 ,
, 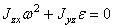 , откуда
, откуда 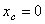 ,
, 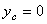 ,
, 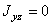 ,
, 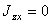 , это означает, что центр тяжести должен находиться на оси
вращения тела и ось вращения тела z должна
быть главной осью инерции тела. Т.е. ось вращения должна являться главной
центральной осью инерции тела (ось, которая проходит через центр масс тела, и
центробежные моменты инерции с индексом этой оси равны нулю). Для выполнения
этого условия проводится специальная балансировка быстро вращающихся тел.
, это означает, что центр тяжести должен находиться на оси
вращения тела и ось вращения тела z должна
быть главной осью инерции тела. Т.е. ось вращения должна являться главной
центральной осью инерции тела (ось, которая проходит через центр масс тела, и
центробежные моменты инерции с индексом этой оси равны нулю). Для выполнения
этого условия проводится специальная балансировка быстро вращающихся тел.
Основы аналитической механики. Принцип возможных
перемещений. Общее уравнение динамики. Уравнение Лагранжа 2-го рода.
Основы аналитической механики
Обобщенные координаты -
независимые величины, заданием которых однозначно определяется положение всех
точек механической системы. Для голономной несвободной механической системы
число обобщенных координат равно числу степеней свободы.
Подавляющее число механизмов,
используемых в технике, является системами с одной степенью свободы,
например: рычаг, лебедка, кривошипно-шатунный механизм, планетарный механизм,
тело, вращающееся вокруг неподвижной оси и т.п. Две
степени свободы имеет центробежный
регулятор. Три степени свободы имеет: свободная материальная точка; несвободное
сферически движущееся тело; тело, совершающее плоское движение. Шесть степеней свободы (наибольшее число степеней свободы) имеет свободное
твердое тело в общем случае его движения.
Голономная несвободная механическая система - несвободная механическая система, перемещение
которой в пространстве ограничено голономными (интегрируемыми) связями.
Голономная интегрируемая связь
- связь, описываемая уравнениями в конечной форме или интегрируемыми
дифференциальными уравнениями.
Связь
называется двусторонней, если накладываемые ее на координаты точки ограничения
выражаются в форме равенств, определяющих поверхности, на которых должна
находиться эта точка. Двусторонняя
связь препятствует перемещению точки в
двух противоположных направлениях. Ограничения, накладываемые на координаты
точки односторонней связью, выражаются неравенствами. Односторонняя связь
препятствует перемещению точки тела лишь в одном направлении.
Принцип освобождаемости от связей позволяет рассматривать движение несвободной
материальной точки как движение свободной точки под действием задаваемых сил и
реакций связей.
Возможные (виртуальные) перемещения - воображаемые элементарные (линейные или угловые,
например: 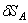 ;
; 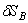 ;
; 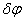 ) перемещения точек тела (тел) механической системы), в действительности допускаемые связями, ограничивающими
перемещение тела (тел) в пространстве.
) перемещения точек тела (тел) механической системы), в действительности допускаемые связями, ограничивающими
перемещение тела (тел) в пространстве.
Для стационарной (с постоянными по времени связями)
механической системы действительные перемещения входят в число ее возможных
перемещений, т.е. являются их частными случаями.
Абсолютно гладкая поверхность - научная абстракция, модель, которой заменяется
реальная шероховатая поверхность, в результате чего не принимается во внимание
трение.
В действительности все поверхности трения достаточно
шероховаты и трение имеет место даже при наличии смазки поверхностей трения. В
связи с этим силу трения - касательную составляющую полной реакции поверхности
как связи - переносят в группу активных (задаваемых) сил, делая тем самым связь
условно идеальной, что позволяет применять для решения ряда задач принцип возможных
перемещений.
Возможные (виртуальные) перемещения системы (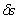 ,
, 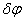 ) – любая
совокупность бесконечно малых перемещений точек системы, допускаемых в данный
момент наложенными на систему связями. Возможные перемещения рассматривают как
величины первого порядка малости, пренебрегая при этом величинами высших
порядков малости. Т.е. криволинейные перемещения точек заменяют прямолинейными
отрезками, отложенными по касательным к их траекториям. Возможные перемещения
от действующих сил не зависят.
) – любая
совокупность бесконечно малых перемещений точек системы, допускаемых в данный
момент наложенными на систему связями. Возможные перемещения рассматривают как
величины первого порядка малости, пренебрегая при этом величинами высших
порядков малости. Т.е. криволинейные перемещения точек заменяют прямолинейными
отрезками, отложенными по касательным к их траекториям. Возможные перемещения
от действующих сил не зависят.
Число
независимых между собою возможных перемещений системы называется числом степеней свободы этой системы. Например. шар на плоскости может перемещаться в любом направлении, но
любое его возможное перемещение может быть получено как геометрическая сумма
двух перемещений вдоль двух взаимно перпендикулярных осей. Свободное твердое
тело имеет 6 степеней свободы.
Возможная (виртуальная) работа 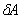 – элементарная работа,
которую, действующая на матер.точку сила могла бы
совершить на возможном перемещении этой точки.
– элементарная работа,
которую, действующая на матер.точку сила могла бы
совершить на возможном перемещении этой точки.
Связи являются идеальными, если сумма элементарных работ реакций этих связей при любом возможном
перемещении системы равна нулю, т.е.  . Например, абсолютно гладкая поверхность, шероховатая
поверхность в случае качения без скольжения.
. Например, абсолютно гладкая поверхность, шероховатая
поверхность в случае качения без скольжения.
Принцип возможных перемещений:
для равновесия механической системы с идеальными связями необходимо и
достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил
при любом возможном перемещении была равна нулю. 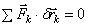 или в проекциях:
или в проекциях: 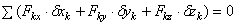 .
.
Принцип возможных перемещений дает в общей форме
условия равновесия для любой механической системы, дает общий метод решения
задач статики.
Если система имеет несколько степеней
свободы, то уравнение принципа возможных перемещений составляют для каждого из
независимого перемещений в отдельности, т.е. будет столько уравнений, сколько
система имеет степеней свободы.
Общее уравнение динамики 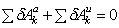 – при движении системы с идеальными связями в
каждый данный момент времен сумма элементарных работ всех приложенных активных
сил и всех сил инерции на любом возможном перемещении системы будет равна нулю.
Уравнение использует принцип возможных перемещений и принцип Даламбера и
позволяет составить дифференциальные уравнения движения любой механической
системы. Дает общий метод решения задач динамики. Последовательность составления:
а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно
прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные
перемещения; в) составляют уравнения принципа возможных перемещений, считая систему
находящейся в равновесии.
– при движении системы с идеальными связями в
каждый данный момент времен сумма элементарных работ всех приложенных активных
сил и всех сил инерции на любом возможном перемещении системы будет равна нулю.
Уравнение использует принцип возможных перемещений и принцип Даламбера и
позволяет составить дифференциальные уравнения движения любой механической
системы. Дает общий метод решения задач динамики. Последовательность составления:
а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно
прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные
перемещения; в) составляют уравнения принципа возможных перемещений, считая систему
находящейся в равновесии.
Уравнения Лагранжа 2-го рода: 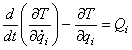 , (i=1,2…s) – дифференциальные уравнения второго порядка, s – число степеней свободы системы (число независимых
координат);
, (i=1,2…s) – дифференциальные уравнения второго порядка, s – число степеней свободы системы (число независимых
координат); 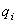 – обобщенная
координата (перемещение, угол, площадь и др.);
– обобщенная
координата (перемещение, угол, площадь и др.); 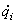 – обобщенная
скорость (линейная скорость, угловая, секторная и др.),
– обобщенная
скорость (линейная скорость, угловая, секторная и др.),
Т = Т(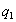 ,
,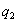 ,…,
,…,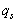 ,
,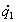 ,
,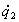 …
…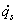 ,t) – кинетическая
энергия системы, Qi –
обобщенная сила (сила, момент и др.), ее размерность зависит от размерности
обобщенной координаты и размерности работы.
,t) – кинетическая
энергия системы, Qi –
обобщенная сила (сила, момент и др.), ее размерность зависит от размерности
обобщенной координаты и размерности работы.
Для вычисления обобщенной силы, например Q1,
задаем возможное перемещение, при котором все вариации обобщенных координат, кроме 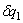 , равны нулю:
, равны нулю:
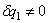 ,
, 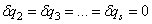 . Вычисляем на этом перемещении возможную работу
. Вычисляем на этом перемещении возможную работу 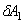 всех активных сил,
приложенных к системе. Имея
всех активных сил,
приложенных к системе. Имея 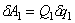 , находим
, находим 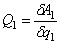 .
.
Если силы, действующие на систему,
потенциальные (консервативные) (например, силы тяжести, силы упругости), то 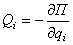 ,
, 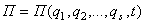 – потенциальная
энергия.
– потенциальная
энергия.
Вводится
функция Лагранжа: L = T – П, тогда 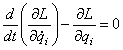 – уравнения Лагранжа
второго рода для консервативной системы. При стационарных связях (связях, не
зависящих от времени) t
не входит в выражение для
кинетической энергии, тогда
– уравнения Лагранжа
второго рода для консервативной системы. При стационарных связях (связях, не
зависящих от времени) t
не входит в выражение для
кинетической энергии, тогда 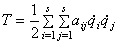 – квадратичная форма
обобщенных скоростей,
– квадратичная форма
обобщенных скоростей, 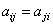 – коэффициенты инерции. Квадратичная форма всегда положительна.
– коэффициенты инерции. Квадратичная форма всегда положительна.
Гироскопы.
Гироскопом называется тяжелое
твердое тело, вращающееся вокруг оси материальной симметрии, одна из точек
которой неподвижна.
Кинетический момент гироскопа
относительно неподвижной точки O направлен вдоль оси симметрии гироскопа и
равен 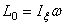 , где
, где 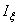 – момент инерции гироскопа.
– момент инерции гироскопа.
Гироскоп с тремя степенями свободы обладает способностью противодействовать силам,
стремящимся изменить направление его оси вращения.
Под действием силы 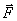 неподвижный гироскоп начинает вращаться вокруг оси,
перпендикулярной плоскости, проходящей через линию действия силы
неподвижный гироскоп начинает вращаться вокруг оси,
перпендикулярной плоскости, проходящей через линию действия силы 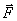 и неподвижную точку C.
После прекращения действия силы гироскоп продолжает вращаться по инерции вокруг
этой оси с постоянной угловой скоростью, которую он приобрел под действием силы
и неподвижную точку C.
После прекращения действия силы гироскоп продолжает вращаться по инерции вокруг
этой оси с постоянной угловой скоростью, которую он приобрел под действием силы
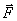 . Под действием силы
. Под действием силы 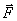 смещение оси гироскопа происходит не по направлению действия
силы, а по направлению ее момента, перпендикулярно направлению силы. После
прекращения действия силы гироскоп вращается вокруг своей оси симметрии,
отклоненной от первоначального положения на угол
смещение оси гироскопа происходит не по направлению действия
силы, а по направлению ее момента, перпендикулярно направлению силы. После
прекращения действия силы гироскоп вращается вокруг своей оси симметрии,
отклоненной от первоначального положения на угол 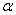 .
.
Ось симметрии гироскопа вращается вокруг неподвижной
оси OZ с некоторой угловой скоростью 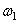 , описывая коническую поверхность. Это движение гироскопа
называется регулярной прецессией, а угловая скорость
, описывая коническую поверхность. Это движение гироскопа
называется регулярной прецессией, а угловая скорость 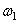 – угловой скоростью прецессии. Угловая скорость прецессии
– угловой скоростью прецессии. Угловая скорость прецессии 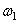 тем меньше, чем больше
угловая скорость
тем меньше, чем больше
угловая скорость 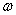 вращения гигроскопа
вокруг его оси симметрии
вращения гигроскопа
вокруг его оси симметрии 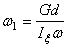 .
.
Гироскоп с двумя степенями свободы не обладает
способностью противодействовать изменению направления его оси вращения.
Гироскопический момент МГ
представляет собой момент пары, составленной силами инерции гироскопа и равен
по величине 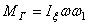 . Гироскопический эффект проявляется всегда, когда изменяется
направление оси быстровращающегося гироскопа.
. Гироскопический эффект проявляется всегда, когда изменяется
направление оси быстровращающегося гироскопа.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов