Главная
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ
РЕШЕНИЯ ЗАДАЧ ПО ДИНАМИКЕ
Динамика относительного движения материальной точки
Второй закон
динамики и полученные на его основе уравнения и теоремы верны только для так
называемого абсолютного движения точки, то есть движения по отношению к
инерциальной (неподвижной) системе отсчета.
Изучим движение материальной точки относительно неинерциальной системы отсчета,
то есть подвижной системы отсчета. Рассмотрим материальную точку 
, движущуюся под действием приложенных к ней сил 
, являющихся результатом взаимодействия точки с другими
телами. Будем изучать движение этой точки по отношению к осям 
, которые в свою очередь каким-то известным нам образом
движутся относительно инерциальной системы отсчета (неподвижных осей) 
(рис.1).
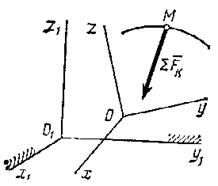
Рис.1
Движение точки относительно системы называется абсолютным,
а движение этой точки относительно системы - относительным.
Движение подвижной системы относительно
неподвижной системы называется переносным
движением.
Считая, что переносное движение
системы и система сил 
известны, основное
уравнение динамики для абсолютного движения точки запишется в виде
,
(1)
где
- абсолютное ускорение точки , а 
- геометрическая сумма приложенных к точке сил.
Из кинематики известно, что
где
- соответственно
относительное, переносное и кориолисово ускорения
точки .
Подставляя это значение 
в равенство (1)
получим
. (2)
Введем два вектора 
,
численно
равные 
и 
и
направленные противоположно ускорениям 
и 
. Эти векторы
назовем переносной и кориолисовой силами инерции.
Подставим эти векторы в уравнение
(2)
. (3)
Уравнение (3) представляет собой основное уравнение
динамики относительного движения материальной точки. Сопоставив
(1) и (3) заключаем: в случае
непоступательного переносного движения относительное движение материальной
точки можно рассматривать как абсолютное, если к действующим на точку силам
присоединить переносную и кориолисову силы инерции.
Это сопоставление показывает также, что в инерциальной
системе отсчета ускорение точки является лишь результатом действия на нее сил,
в то время как в неинерциальной системе ускорение является как результатом
действия на нее сил, так и результатом движения самой системы отсчета.
Спроектировав (3) на оси подвижной системы отсчета , получим дифференциальные уравнения относительного движения
материальной точки
,
,
(4)
.
Рассмотрим частные случаи относительного движения
материальной точки, соответствующее различным видам
переносного движения.
1. Переносное движение – неравномерное вращение тела вокруг
неподвижной оси. В этом случае переносное ускорение 
равно геометрической
сумме вращательного и центростремительного ускорений
.
Тогда уравнение (3) принимает вид
, (5)
где 
, 
.
2. Переносное движение – равномерное вращение тела
вокруг неподвижной оси. В этом случае 
, а следовательно, 
. Тогда уравнение (3) запишется в виде
.
(6)
3. Переносное движение – поступательное неравномерное
криволинейное движение. В этом случае 
и 
, а потому
.
(7)
4. Переносное движение – поступательное
прямолинейное и равномерное движение. В
этом случае 
и 
, а потому
. (8)
Сопоставив (8) и (1) замечаем, что их правые части
совпадают. Это говорит о том, что подвижная система отсчета является в этом случае
тоже инерциальной системой.
Рассмотрим пример решения задачи.
Пример 1. Шарик массы 
, прикрепленный к концу горизонтальной пружины, коэффициент
жесткости которой 
, находится в положении равновесия в трубке на расстоянии 
от вертикальной оси 
. Определить закон относительного движения шарика, если
трубка начинает вращаться вокруг вертикальной оси с постоянной угловой
скоростью 
. Точка 
на оси вращения
соответствует положению ненагруженной пружины (рис.2).
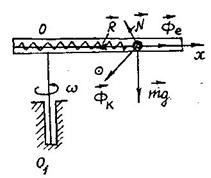
Рис.2
Решение.
Поместим начало координат оси 
в точке . Изобразим шарик в текущий момент времени в положении, отстоящем
от начала координат на расстоянии . Чтобы найти относительное движение шарика, приложим к нему
силу упругости пружины 
, силу тяжести 
, переносную силу инерции 
, а также кориолисову силу инерции 
и реакцию стенки 
, расположенные в плоскости, перпендикулярной к оси трубки.
Дифференциальное уравнение относительного движения (4)
для рассматриваемой задачи имеет вид
.
Учитывая, что 
, получим
,
или 
(9)
где 
.
Рассмотрим случай, когда 
. Тогда решение дифференциального уравнения (9) имеет вид
, (10)
где 
.
Для определения 
и 
, найдем относительную скорость шарика
.
(11)
Подставляя в (10) и (11) начальные условия 
, получим
.
Окончательно, закон относительного движения шарика
представится в виде
.
Работа силы. Мощность
Для характеристики действия силы на тело при некотором
его перемещении, вводится мера этого действия, называемая работой силы. Сначала
введем понятие об элементарной работе.
Элементарной
работой силы 
, приложенной в точке (рис.3), называется
скалярная величина
,
(12)
где 
- проекция силы на направление
скорости 
точки ; 
-модуль элементарного перемещения точки .
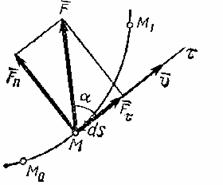
Рис.3
Так как =
, то из (12) получим
, (13)
где 
- угол между и 
.
Если угол острый, то работа
положительна, а если угол тупой – отрицательна.
При 
, то есть если сила направлена перпендикулярно перемещению,
то элементарная работа силы равна нулю.
Если учесть, что 
, где 
- вектор элементарного
перемещения точки, то равенство (13) можно представить в виде
.
(14)
Следовательно, элементарная работа силы равна
скалярному произведению силы на вектор элементарного перемещения точки ее
приложения.
Если в (14) выразить скалярное произведение через
проекции векторов и 
на координатные оси,
то получим аналитическое выражение элементарной работы
, (15)
где 
-координаты точки приложения силы .
Работа силы на любом конечном перемещении 
(рис.3) вычисляется
как предел интегральной суммы соответствующих элементарных работ
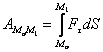, (16)
или
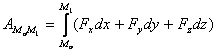. (17)
Следовательно, работа силы на любом конечном
перемещении равна взятому вдоль этого
перемещения интегралу от элементарной работы.
Если величина постоянна, то из (16),
обозначив перемещение через
, получим
. (18)
Если сила постоянна по модулю и направлению (=const), а точка приложения силы движется прямолинейно
(рис.4), то получим
.
(19)
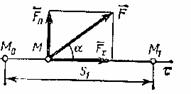
Рис.4
Единицей измерения работы является в СИ – 1 джоуль
(1Дж=1 Нм).
Мощностью называется величина, определяющая работу, совершаемую
силой в единицу времени. Если работа совершается равномерно, то мощность 
, где 
- время, в течение
которого произведена работа. В общем случае
(20)
Мощность равна произведению касательной составляющей
силы на скорость.
Единицей измерения мощности в СИ является ватт
(1Вт=1Дж/с).
В заключении приводим некоторые примеры вычисления
работы.
1.Работа силы
тяжести.
Пусть точка , на которую действует сила тяжести , перемещается из положения 
в положение 
(рис.5).
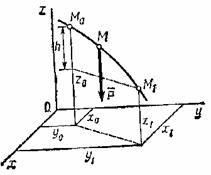
Рис.5
Работа силы тяжести равна взятому со знаком плюс или
минус произведению модуля силы тяжести на вертикальное перемещение точки ее
приложения
(21)
2. Работа
силы упругости.
Рассмотрим груз , прикрепленный к свободному концу пружины (рис.6).
Примем за начало координат точку , в которой пружина не напряжена, т.е. 
- длина ненапряженной пружины. Найдем работу, совершаемую
силой упругости при перемещении из положения 
в положение 
.
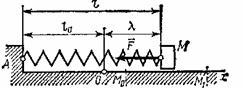
Рис.6
Воспользовавшись формулой (17), получим
, (22)
где 
- коэффициент жесткости пружины;
и 
- деформация пружины
соответственно в положении 
и 
.
Рассмотрим пример.
Пример 2. Груз веса подвешен на нити длины
. Нить вместе с грузом отклоняют от вертикали на угол 
и отпускают без
начальной скорости (рис.7). При движении на груз действует сила сопротивления , которую приближенно заменяем ее средним значением 
. Вычислить сумму работ сил при перемещении груза из
положения в положение , когда нить образует с вертикалью угол .
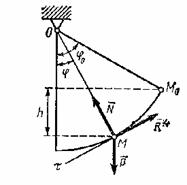
Рис.7
Решение.
На груз действуют сила тяжести , реакция нити и сила сопротивления,
представленная ее средним значением 
. Работу силы определим по формуле
(21)
.
Так как проекция силы на касательную ось равна нулю, то есть 
, то 
. Работу силы вычислим по формуле
(18)
,
где - длина дуги .
Так как =
, то 
. Окончательно, получим
.
Пример 3. С поверхности Земли вертикально
вверх пущена ракета со скоростью v0=5 км/с. На какую высоту она
поднимется?
Решение.
На ракету действует сила притяжения Земли, которая по закону всемирного
тяготения равна: 
,
где m – масса ракеты, МЗ – масса Земли, 
– расстояние до центра
Земли, RЗемли=6,4.106 м. Элементарная работа
против силы тяжести при перемещении ракеты вверх на dr
равна: dA=Fdr; полная работа при перемещении ракеты от поверхности
Земли до высоты h рассчитывается интегрированием:
.
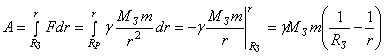По закону сохранения энергии кинетическая энергия,
которой обладала ракета на Земле, будет израсходована на работу против силы
притяжения: 
. Тогда получим уравнение:
.
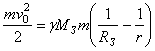После сокращения на m и
подстановки получим выражение для
высоты:
.
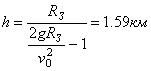Здесь учтено, что 
- ускорение свободного
падения на поверхности Земли.
Пример 4. Шар массой m=
Решение. Будем
считать стенку массивной и неподвижной. Тогда по закону сохранения энергии
выделившаяся при ударе теплота равна изменению механической энергии шара:
. (1)
Полная кинетическая энергия катящегося тела равна
сумме кинетической энергии поступательного движения центра
масс тела и кинетической энергии вращательного движения тела
относительно центра масс, так как качение тела является суперпозицией этих двух
движений:
. (2)
Так как качение происходит без проскальзывания, то
линейная скорость движения центра масс и угловая скорость вращения связаны
соотношением:
, (3)
где R – радиус шара, J – момент инерции шара относительно оси, проходящей через центр
масс:
. (4)
Подставив (3) и (4) в (2), получим формулу для энергии
катящегося шара:
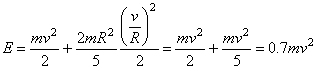. (5)
Аналогично, начальная кинетическая энергия шара:
. (6)
Подставляем (5) и (6) в (1) и получаем искомую
теплоту:
Дифференциальные уравнения плоскопараллельного движения
твердого тела
Плоским или
плоскопараллельным движением твердого тела называется такое движение, при
котором каждая точка тела движется в плоскости, параллельной некоторой
неподвижной плоскости.
Положение тела, совершающего плоскопараллельное
движение, определяется в любой момент времени положением полюса и углом
поворота вокруг полюса. Задачи динамики решаются проще, если за полюс принять
центр масс тела и определять
положение тела координатами 
и 
и
углом 
. На рис.8 изображено сечение тела плоскостью, параллельной
плоскости движения и проходящей через центр масс .
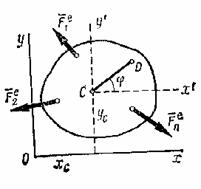
Рис.8
Пусть на тело действуют внешние силы 
, лежащие в плоскости этого сечения. Тогда уравнения движения
точки находим по теореме о
движении центра масс
,
(23)
где 
- ускорение центра масс, а вращательное движение вокруг
центра будет определяться
уравнением
,
(24)
где 
и 
- соответственно момент инерции тела
и главный момент внешних сил относительно оси, проходящей через центр масс перпендикулярно
плоскости 
.
Спроектировав обе части равенства (23) на координатные
оси, окончательно получим
, 
, 
, (25)
где - масса тела; 
и 
-проекции ускорения центра масс на координатные оси.
Уравнения (25) представляют собой дифференциальные
уравнения плоскопараллельного движения твердого тела. Интегрируя эти дифференциальные
уравнения второго порядка, найдем 
и в функциях от времени 
и, следовательно,
найдем движение тела.
Заметим, что с помощью уравнений (25) в случае, когда
известен закон движения, можно найти главный вектор и главный момент внешних
сил.
При несвободном движении, когда траектория центра масс
известна, уравнения движения точки удобнее составлять в
проекциях на касательную 
и главную нормаль 
к этой траектории.
Тогда вместо (25) получим
, 
, .
Рассмотрим пример.
Пример 5. Однородный круглый цилиндр радиуса 
и массы скатывается без
скольжения под действием силы тяжести по негладкой плоскости, наклоненной к
горизонту под углом (рис.9). Найти
ускорение центра масс цилиндра.
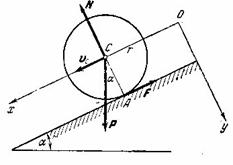
Рис.9
Решение.
На цилиндр действуют следующие силы: вес , нормальная реакция плоскости , линия действия которой проходит через центр тяжести
цилиндра , и сила трения , направленная вверх по наклонной плоскости. Взяв
координатные оси, как указано на рис.9, составим дифференциальные уравнения
плоского движения цилиндра
а)
,
б)
,
в)
,
где - момент инерции цилиндра относительно оси, проходящей через
его центр тяжести перпендикулярно
плоскости .
Так как во все время движения 
, то
.
Тогда из уравнения (б) получим
.
Так как цилиндр катится без скольжения, то точка 
будет являться его
мгновенным центром скоростей, а следовательно, 
. Тогда
.
Поэтому, уравнение (а) примет вид
.
Исключив 
из этого уравнения и
уравнения (в), получим
.
Учитывая, для однородного цилиндра 
, последнее уравнение примет вид
.
Следовательно, искомое ускорение центра масс цилиндра
будет равно
.
Принцип Даламбера для
материальной точки и для механической системы
Предположим, что материальная точка под действием системы
сил 
движется с ускорением (рис.10)
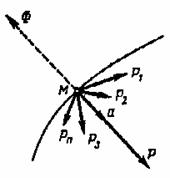
Рис.10
Основное уравнение динамики имеет вид
Перенесем член 
из левой части
уравнения в правую
.
Введем обозначение 
. Сила 
называется силой
инерции материальной точки и направлена противоположно ускорению точки.
Тогда последнее уравнение примет вид
. (26)
Последнее соотношение формулируется так:
геометрическая сумма всех приложенных к точке сил и силы инерции этой точки
равна нулю.
Как известно, в действительности, сила инерции
материальной точки приложена не к ней, а к телу, сообщающему точке ускорение.
Приложение силы инерции к точке является лишь условным приемом, сводящим задачу
динамики по форме решения к задаче статики.
При изучении движения несвободной механической
системы, так же как и при изучении движения одной несвободной точки,
применяется принцип освобождаемости от связей. По
этому принципу имеющиеся связи отбрасывают, заменяя их действие
соответствующими реакциями.
Рассмотрим несвободную механическую систему, состоящую
из материальных точек.
Применив к каждой точке 
этой системы принцип
Даламбера, получим
, (27)
где 
- равнодействующая
задаваемых сил, приложенных к точке ; 
- равнодействующая реакций связей, приложенных к этой точке; 
- сила инерции материальной точки .
Сложим все уравнений (5)
.
(28)
Здесь 
- главный вектор задаваемых сил; 
- главный вектор реакций связей; 
- главный вектор сил инерции точек системы.
Подставляя эти значения в уравнение (6), будем иметь
.
(29)
Из уравнения (29) следует, что в любой момент времени
для всякой несвободной механической системы геометрическая сумма главных
векторов задаваемых сил, реакций связей и сил инерции материальных точек
системы равна нулю.
Применение уравнения (29), вытекающее из принципа
Даламбера, упрощает процесс решения задач, так как эти уравнения не содержат
внутренних сил.
В проекциях на координатные оси равенство (29) дает
уравнения, аналогичные уравнениям статики.
В заключение следует подчеркнуть, что при изучении
движения по отношению к инерциальной системе отсчета, силы инерции вводятся
только тогда, когда для решения задач применяется принцип Даламбера.
Ниже приводятся формулы для приведения сил инерции
твердого тела при различных случаях его движения.
1. Поступательное движение. В этом случае ускорения всех точек тела одинаковы и
равны ускорению центра масс тела. Поэтому, силы
инерции твердого тела приводятся к равнодействующей, равной 
и проходящей через
центр масс тела.
2. Вращение вокруг оси, проходящей через центр масс
тела. В этом случае 
, так как 
. Следовательно, система сил инерции тела приводится к одной
паре сил с моментом 
, где - момент инерции тела относительно оси, проходящей через
центр масс перпендикулярно плоскости симметрии тела; 
- угловое ускорение тела.
3. Плоскопараллельное движение. В этом случае система сил инерции
тела приводится к лежащим в плоскости симметрии силе, равной и приложенной в
центре масс тела, и паре с
моментом 
.
В приведенных выше формулах для
(или 
) знак минус указывает на то, что
вектор (или ) направлен противоположно ускорению центра масс тела (или
угловому ускорению тела).
Рассмотрим несколько примеров.
Пример 6. Два груза веса 
и 
каждый, связанные
нитью, движутся по горизонтальной плоскости под действием силы 
, приложенной к первому грузу (рис.11, а). Коэффициент трения
грузов о плоскость равен 
. Определить ускорение
грузов и напряжение нити.
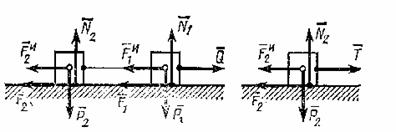
а) Рис.11 б)
Решение.
Изобразим все действующие на систему внешние силы (,,
,
,
,
). Прибавим к этим силам силы инерции грузов. Так как
оба груза движутся поступательно с одним и тем же ускорением, то
, 
.
Модули сил трения равны: 
, 
.
Согласно принципу Даламбера полученная система сил должна
находиться в равновесии. Составив уравнение равновесия в проекции на
горизонтальную ось, получим
.
Отсюда 
.
Очевидно, что грузы будут двигаться, если 
.
Так как натяжение нити является в рассматриваемой
системе силой внутренней, то для ее определения расчленяем систему и применяем
принцип Даламбера, например, ко второму грузу (рис.11, б). На этот груз
действуют сила , нормальная реакция , сила трения и натяжение нити 
. Присоединив к ним силу инерции 
и составив уравнение
равновесия в проекции на горизонтальную ось, получим
.
Подставив сюда найденное ранее значение , окончательно найдем значение
.
Интересно, что натяжение нити не зависит от силы
трения и при одном и том же суммарном весе системы будет тем меньше, чем меньше
вес второго (заднего) груза. Поэтому, например, в железнодорожном составе
выгоднее в его головной части помещать более тяжелые вагоны, а в хвостовой
части – более легкие.
Пример 7. Невесомый стержень 
длинны 
, несущий на каждом из своих концов груз веса 
, жестко скреплен в середине с вертикальной осью, опирающейся
на подпятник и подшипник 
и вращающийся с
постоянной угловой скоростью . Угол между осью и стержнем равен , расстояние 
. Найти горизонтальные реакции 
и 
подпятника и
подшипника в точках и и
вертикальную реакцию 
подпятника в точке (рис.12).
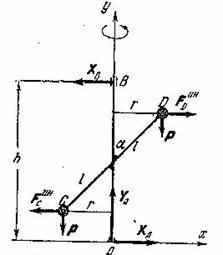
Рис.12
Решение.
Так как грузы вращаются равномерно, то их касательные ускорения, а следовательно, и их касательные силы инерции равны нулю.
Приложим к грузам нормальные силы инерции, направленные по радиусам вращения
грузов от оси вращения, равные по модулю
.
Составим три уравнения равновесия плоской системы сил,
которым, согласно принципу Даламбера, должны удовлетворять заданные силы , силы инерции и реакции в точках и . Спроектировав все эти силы на оси 
и 
, получим
.
Составим затем сумму моментов всех этих сил
относительно точки
.
Решив эти уравнения, получим 
и 
.
Принцип возможных
перемещений
Возможными
(или виртуальными) перемещениями
несвободной механической системы называются воображаемые бесконечно малые
перемещения, допускаемые в данный момент наложенными на систему связями.
Возможные перемещения точек системы рассматривают как
величины первого порядка малости, пренебрегая при этом величинами высших
порядков малости. Поэтому криволинейные перемещения точек заменяют
прямолинейными отрезками, отложенными по касательным к траекториям точек, и
обозначают 
. Так, например, возможным перемещением рычага 
(рис.13) является его
поворот на бесконечно малый угол 
вокруг точки . При этом повороте точки и должны переместиться
по дугам окружностей 
и 
.
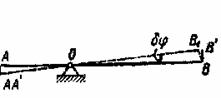
Рис.13
С точностью до величин первого порядка малости эти
перемещения заменяют возможными перемещениями 
и 
в виде прямолинейных
отрезков, отложенных по касательным к траекториям точек, а по величине равных
, 
.
Силы, действующие на несвободную точку или механическую
систему, делят на задаваемые силы и реакции связей.
Рассмотрим механическую систему, состоящую из материальных точек , 
, подчиненную связям: реакции связей обозначим 
(рис.14). Сообщим
системе какое-либо возможное перемещение; возможные перемещения точек системы
обозначим 
. Вычислим сумму работ реакций на этих перемещениях.
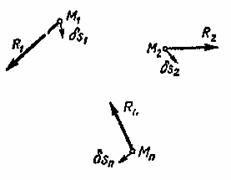
Рис.14
Если сумма работ реакций связей на любом возможном
перемещении системы равна нулю, то такие связи называются идеальными.
Согласно этому определению, для идеальных связей
.
(30)
При решении задач статики для определения реакций
связей использовались уравнения равновесия твердого тела. При этом реакции
связей не выделялись из общего числа приложенных к телу сил. В сложных
несвободных механических системах определение реакций связей с помощью
уравнений равновесия становится громоздким. В этих случаях целесообразно
использовать принцип возможных
перемещений, который формулируется так:
Необходимое и
достаточное условие равновесия системы сил, приложенной к механической системе,
подчиненной стационарным, двусторонним и идеальным связям, заключается в
равенстве нулю суммы элементарных работ задаваемых сил на любом возможном
перемещении системы из рассматриваемого ее положения
. (31)
Если в каждую точку системы из некоторого
центра провести вектор 
, то возможное перемещение этой точки 
будет соответствующим
возможным приращением радиуса вектора точки
.
Тогда уравнение работ (31) примет вид
(32)
Если воспользоваться аналитическим выражением
элементарной работы, то уравнение (3) можно представить в виде
, (33)
где 
и 
- проекции соответственно задаваемой силы и возможного
перемещения на неподвижные оси декартовых координат.
Если система имеет одну степень свободы, то одно из
равенств (31), (32) или (33) устанавливает сразу условие равновесия задаваемых
сил, приложенных к системе. Если же система имеет несколько степеней свободы,
то уравнения работ составляют для каждого независимого перемещения системы в
отдельности. Таким образом, получается столько условий равновесия системы,
сколько степеней свободы она имеет.
Рассмотрим несколько примеров.
Пример 8. К рукоятке винтового пресса
приложена пара 
), лежащая в горизонтальной плоскости, причем силы этой пары
направлены перпендикулярно к . Найти силу, сжимающую прессуемое тело, если шаг винта равен
, а длина = (рис.15).
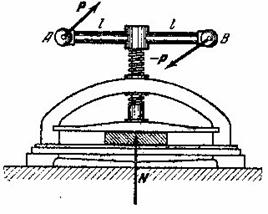
Рис.15
Решение.
Обозначим через вертикальную реакцию сжимаемого тела и дадим системе
возможное перемещение, для чего повернем рукоятку на угол по часовой стрелке
(если смотреть сверху). При этом система кроме этого вращательного перемещения
получит и поступательное перемещение, равное по модулю 
и направленное по
вертикали вниз. Уравнение, выражающее условие равновесия системы, будет иметь
вид
.
Отсюда
.
Найдем теперь зависимость между
и . Так как поступательное перемещение
винта пропорционально углу поворота его вокруг винтовой оси, и так как винт при
повороте на угол, равный 
, перемещается вдоль оси на расстояние, равное шагу , то получим следующее соотношение
.
Отсюда находим
.
Подставив это значение в выражение для 
, окончательно получим
.
Искомая сила, сжимающая тело, равна по модулю
найденной реакции .
Пример 9. Найти условие
равновесия кривошипно-шатунного механизма под действием горизонтальной силы , приложенной к ползуну , и силы , приложенной к пальцу кривошипа и перпендикулярной к 
(рис.16).
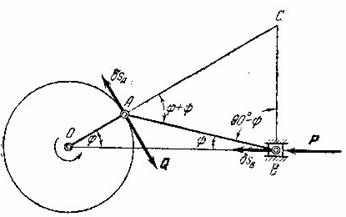
Рис.16
Решение.
Сообщив механизму возможное перемещение и приравнивая
нулю сумму работ и на этом перемещении,
получим
.
Отсюда получим
,
где 
и 
- модули возможных перемещений точек и , при этом перемещение точки направлено по 
, а перемещение точки - по касательной к ее
траектории, то есть перпендикулярно к кривошипу . Чтобы найти зависимость между и , построим мгновенный центр скоростей шатуна , который находится в точке пересечения перпендикуляров 
и 
к направлениям
возможных перемещений (или скоростей) точек
и . Согласно свойству мгновенного центра скоростей, эти
перемещения пропорциональны расстояниям точек и от мгновенного центра
скоростей шатуна, то есть
,
откуда
.
Обозначим угол 
через , угол наклона шатуна - через
; тогда
.
Из треугольника 
по теореме синусов
находим
.
Следовательно,
.
Таково условие, которому должны удовлетворять силы 
и при равновесии.
Общее уравнение динамики
Согласно принципу Даламбера для несвободной
механической системы геометрическая сумма главных векторов задаваемых сил,
реакций связей и сил инерции материальных точек системы равна нулю. Отсюда на
основании принципа возможных перемещений следует, что сумма элементарных работ
всех этих сил при всяком возможном перемещении
системы равна нулю. Но если на систему наложены идеальные связи, то сумма работ
реакций таких связей при всяком возможном перемещении системы равна нулю.
Поэтому, в случае идеальных связей сумма элементарных работ задаваемых сил и
сил инерции точек системы при любом ее возможном перемещении равна нулю.
С учетом (33), будем иметь
. (34)
Представим проекции сил инерции 
, 
и 
в виде
,
(35)
где 
- проекции ускорения точки системы на координатные оси; 
- масса 
-ой точки.
Подставив (35) в равенство (34), окончательно получим
.
(36)
Уравнение (36), полученное на основании двух основных
принципов механики – принципа Даламбера и принципа возможных перемещений –
называется общим уравнением динамики.
От общего уравнения статики (33) оно
отличается только тем, что, кроме проекций задаваемых сил на
координатные оси, в него входят еще проекции сил инерции на те же оси.
Заметим, что общее уравнение динамики позволяет
составлять дифференциальные уравнения движения любой механической системы.
Рассмотрим пример.
Пример 10. Барабаны радиусов 
и 
, соединенные между собой жестко, могут вращаться вокруг
горизонтальной оси. На барабан намотаны нерастяжимые нити, к концам которых
подвешены груз веса 
и груз веса 
. Система движется под действием сил тяжести грузов.
Определить угловое ускорение барабанов, пренебрегая их массами и массой нитей
(рис.17а).
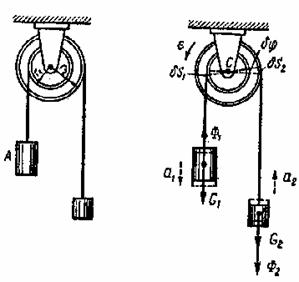
а) Рис.17 б)
Решение.
Предположим, что соотношение весов грузов таково, что барабаны вращаются с
угловым ускорением в направлении,
обратном направлению вращения часовой стрелки (рис.17б).
Заданная механическая система имеет одну степень
свободы и состоит из двух грузов, движущихся поступательно. Нити и барабаны,
массы которых не учитываются, являются связями.
Покажем заданные силы тяжести 
и 
. Силы инерции точек каждого груза, движущегося
поступательно, приводятся к равнодействующей силе, приложенной в центре масс
груза. Приложим к грузам условно силы инерции 
и 
, направив их противоположно ускорениям грузов 
и 
. Так как ускорения грузов равны вращательным ускорениям
точек ободов барабанов, то модули сил инерции будут
равны
;
.
Сообщим системе возможное перемещение, повернув
барабаны на угол по направлению их
действительного вращения. Возможные перемещения грузов равны возможным
перемещениям точек ободов барабанов
.
Составим общее уравнение динамики в виде (5)
.
Подставив в это уравнение значения возможных
перемещений 
и сил инерции 
, определим угловое ускорение барабанов
.
Пример 11. Через блок, имеющий форму диска, перекинут шнур. К
концам шнура привязаны грузики массой m1=
Решение.
Запишем второй закон Ньютона для поступательного движения в проекции на
вертикальную ось, направленную вверх, для обоих грузиков:
; (1)
; (2)
Здесь учтено, что модули ускорений обоих грузов
одинаковы, так как шнур считаем нерастяжимым.
За положительное направление вращения блока примем
вращение по часовой стрелке; запишем для него закон динамики вращательного
движения:
, (3)
где J– момент инерции сплошного диска (или цилиндра):
; (4)
– угловое ускорение
блока, связано с линейным ускорением
обода блока и шнура (предполагаем, что проскальзывания нет):
, (5)
здесь R –
радиус блока; модули моментов сил натяжения шнура относительно оси вращения:
, (6)
(7)
Решая систему уравнений (1-7), получим:
,
откуда находим ускорение:
,
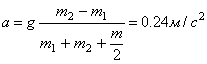а затем из (1) и (2) – силы натяжения шнура:
H;
Н.
Вынужденные колебания материальной
точки
Колебательное движение материальной точки происходит
при условии, если на точку , отклоненную от положения покоя , действует сила , стремящаяся вернуть точку в это положение. Такая сила
называется восстанавливающей.
Колебания, совершающиеся под действием только
восстанавливающей силы, называются свободными.
Рассмотрим важный случай колебаний, возникающих когда
на точку кроме
восстанавливающей силы (рис.18),
пропорциональной расстоянию от положения покоя , действует еще периодически изменяющаяся , проекция которой на ось 
равна
(37)
Рис.18
Эта сила называется возмущающей силой, а колебания, происходящие при действии такой силы называются вынужденными. Величина 
в равенстве (37)
является частотой возмущающей силы.
Учитывая, что проекция восстанавливающей силы на ось равна 
, дифференциальное уравнение движения точки запишется в виде
, (38)
где - масса точки; - коэффициент пропорциональности, характеризующий
восстанавливающую силу.
Разделим обе части последнего уравнения на и введем обозначения
. (39)
Тогда уравнение (38) примет вид
.
(40)
Уравнение (40) является дифференциальным уравнением
вынужденных колебаний точки при отсутствии сопротивления.
Как известно из теории дифференциальных уравнений, его
решением будет 
, где 
- общее решение уравнения (40) без правой части, то есть
решение уравнения свободных колебаний, а 
- какое-нибудь частное решение неоднородного уравнения (40).
Из теории свободных колебаний известно, что 
, где и - постоянные
интегрирования, определяемые из начальных условий.
Полагая, что 
, будем искать решение в виде 
,
где - постоянная величина,
которую надо подобрать так, чтобы равенство (40) обратилось в тождество.
Подставляя значение и его второй
производной в уравнение (40), получим
.
Это равенство будет выполняться при любом , если 
, откуда
.
Таким образом, искомое частное решение будет
.
(41)
Так как , то общее решение уравнения (40) имеет окончательно вид
. (42)
Решение (42) показывает, что колебания точки слагаются
в этом случае из:
1) колебаний с амплитудой (зависящей от
начальных условий) и частотой 
, называемых собственными
колебаниями; 2) колебаний с амплитудой (не зависящей от
начальных условий) и частотой , которые называются вынужденными
колебаниями.
На практике, благодаря неизбежному наличию тех или
иных сопротивлений, собственные колебания будут довольно быстро затухать.
Поэтому основное значение в рассматриваемом движении имеют вынужденные
колебания, закон которых дается уравнением (41).
Как видно, частота вынужденных колебаний
равна частоте возмущающей силы. Амплитуду этих колебаний, если разделить
числитель и знаменатель на 
, можно представить в виде
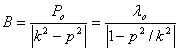, (43)
где согласно (39) 
, т.е. 
есть величина
статического отклонения точки под действием силы 
. Введем обозначения
. (44)
Безразмерный коэффициент 
называют коэффициентом динамичности. Он показывает,
во сколько раз амплитуда вынужденных колебаний (т.е. максимальное
отклонение точки от центра колебаний) больше статического отклонения , и зависит от отношения частот 
.
Из формулы (43) видно, что
подбирая различные соотношения между и , можно получить вынужденные колебания с разными амплитудами.
При 
(или 
амплитуда равна (или близка к ней).
Если величина близка к , амплитуда становится очень
большой. Наконец, когда 
, амплитуда становится очень малой
(практически близка к нулю).
В случае, когда 
, то есть когда частота возмущающей силы равна частоте
собственных колебаний, имеет место так называемое явление резонанса. Формулами
(41), (43) этот случай не описывается, но нетрудно заметить, что размахи
вынужденных колебаний при резонансе будут со временем неограниченно возрастать
так, как это показано на рис.19.
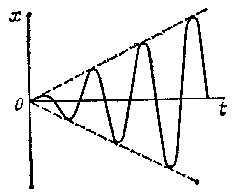
Рис.19
Ниже приводится (без вывода) закон вынужденных колебаний при резонансе () в случае отсутствия сопротивления среды
. (45)
Как видно из (9), размахи вынужденных колебаний при
резонансе действительно возрастают пропорционально времени, и закон этих
колебаний имеет вид, показанный на рис.2.
Из полученных результатов вытекает, что вынужденные
колебания обладают следующими свойствами, отличающими их от собственных колебаний точки:
а) амплитуда вынужденных колебаний от начальных
условий не зависит;
б) частота вынужденных колебаний равна частоте
возмущающей силы и от характеристик колеблющейся системы не зависит
(возмущающая сила «навязывает» системе свою частоту колебаний);
в) даже при малой возмущающей силе ( мало) можно получить
интенсивные вынужденные колебания, если частота близка к (резонанс);
г) даже при больших значениях возмущающей силы
вынужденные колебания можно сделать сколь угодно малыми, если частота будет много больше .
Во многих инженерных сооружениях явление резонанса
крайне нежелательно и его следует избегать, подбирая соотношение между
частотами и так, чтобы амплитуды
вынужденных колебаний были практически равны нулю ().
Противоположный пример мы
имеем в радиотехнике, где резонанс оказывается очень полезным и используется
для отделения сигналов одной радиостанции от сигналов всех остальных (настройка
приемника).
Рассмотрим пример.
Пример 12. Исследовать
вынужденные колебания груза 1 массы , подвешенного на пружине с коэффициентом жесткости , если верхний конец 
пружины совершает
вертикальные колебания по закону 
.
Решение.
Поместим начало координат в положение
статического равновесия груза и направим ось по вертикали вниз
(рис.20).
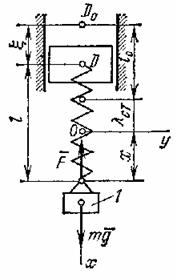
Рис.20
Если обозначить длину недеформированной пружины через 
, то ее длина в произвольный момент времени будет 
, а удлинение 
. Тогда действующая на груз сила упругости
.
Составим
дифференциальное уравнение движения груза
.
Учитывая, что 
, получим
.
Введя обозначение 
, последнее уравнение примет вид
.
Так как полученное уравнение совпадает с уравнением (40),
если в нем считать 
, то, следовательно, груз будет совершать вынужденные
колебания. В данном случае 
, а амплитуда вынужденных колебаний определится по формуле (43).
Если 
(верхний конец пружины
колеблется очень медленно), то согласно (43) и (44) получим, что 
. Груз будет при этом колебаться так, как если бы пружина
была жестким стержнем. При наступает резонанс, и
размахи колебаний начнут сильно возрастать. Наконец, когда будет много больше (
), амплитуда 
. Груз при этом будет оставаться в положении статического
равновесия (в точке ), хотя верхний конец пружины и совершает колебания с
амплитудой 
(частота этих колебаний столь велика, что груз как бы не
успевает за ними следовать).
Пример 13. Найти частоту колебаний груза массой m=0,2 кг, подвешенного на пружине и помещенного в масло, если
коэффициент сопротивления в масле r=0,5 кг/с, а коэффициент жесткости
пружины k=50 Н/м .
Решение.
Колебания груза в масле являются затухающими, их круговая частота:
,
где 
– круговая частота
собственных незатухающих колебаний; 
– коэффициент
затухания. Тогда частота затухающих колебаний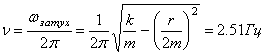 
Элементарная теория удара
При движении тела под действием обычных сил скорости точек
тела изменяются непрерывно, т.е. каждому бесконечно малому промежутку времени соответствует
бесконечно малое приращение скорости. Однако если в числе действующих сил будут
очень большие силы (порядка 
), то приращение скорости за малый промежуток времени окажется величиной
конечной.
Явление, при котором скорости точек тела за очень
малый (близкий к нулю) промежуток времени изменяются на конечную
величину, называется ударом.
Силы, при действии которых происходит удар, будем
называть ударными силами 
. Промежуток времени , в течение которого происходит удар, называют временем удара.
Так как ударные силы очень велики, то в теории удара в
качестве меры взаимодействия тел рассматривают не сами ударные силы, а их
импульсы. Ударный импульс
(46)
является величиной конечной. Импульсы неударных сил за
время будут величинами очень
малыми и ими практически можно пренебречь.
Обозначим скорость точки в начале удара , а скорость в конце удара 
. Тогда теорема об изменении количества движения точки при ударе
запишется в виде
,
(47)
т.е. изменение количества движения материальной точки
за время удара равно сумме действующих на точку ударных импульсов. Уравнение
(47) является основным уравнением теории
удара.
Из полученных результатов следует, что:
а) действием
неударных сил за время удара можно пренебречь;
б) перемещениями точек тела за время удара можно
пренебречь и считать тело во время удара неподвижным;
в) изменения скоростей точек тела за время удара
определяются из уравнения (47).
Значение ударного импульса, появляющегося при
соударении двух тел, зависит не только от их масс и скоростей до удара, но и от
упругих свойств соударяющихся тел. Эти свойства при ударе характеризуются
величиной, называемой коэффициентом восстановления.
Рассмотрим шар, падающий вертикально на неподвижную горизонтальную жесткую плиту (рис.21).
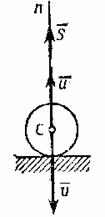
Рис.21
В момент, когда шар достигнет плиты, произойдет удар, называемый
прямым. Считая движение шара поступательным, примем скорости частиц шара в момент
начала удара равными , а в конце удара - . Механическая энергия шара полностью не восстанавливается,
так как часть ее уходит на сообщение шару остаточных деформаций и его
нагревание. Поэтому скорость 
меньше скорости 
.
Величина , равная при прямом ударе тела о неподвижную преграду
отношению модуля скорости в конце удара к модулю скорости в начале удара,
называется коэффициентом восстановления
при ударе.
.
(48)
Значение коэффициента восстановления для разных тел
определяется опытным путем. При изменении скорости не в очень больших
пределах величину можно считать
зависящей только от материала соударяющихся тел.
Различают случай абсолютно упругого удара (
), при котором кинетическая энергия тела после удара
полностью восстанавливается, а также случай абсолютно неупругого удара (
), когда вся кинетическая энергия тела расходуется на его
деформацию и нагревание.
Рассмотрим тело (шар) массы , ударяющееся о неподвижную плиту. Действующей на тело
ударной силой будет при этом реакция плиты; импульс этой силы за время удара
обозначим через 
. Пусть нормаль к поверхности тела в точке его касания с
плитой проходит через центр масс тела. Такой удар тела называется центральным. Если скорость центра масс тела в
начале удара направлена по нормали к плите, то удар будет
прямым, в противном случае – косым.
Составляя, в случае прямого удара, основное уравнение
теории удара (47) в проекции на нормаль (рис.21), получим 
.
Но при прямом ударе 
.
Следовательно,
.
Из равенства (48) получим второе уравнение,
необходимое для решения задачи
.
Подставив это значение в выражение для 
, получим
.
(49)
Как видно из (49), ударный импульс будет тем больше,
чем больше коэффициент восстановления. Чтобы определить среднюю величину
ударной силы (реакции), надо знать время удара , которое находится экспериментально.
Рассмотрим теперь случай косого удара. Пусть в этом
случае скорость центра масс тела в
начале удара образует с нормалью к плите угол , а скорость в конце удара – угол 
(рис.22). Тогда уравнение
(47) в проекциях на касательную и нормаль имеет вид
.
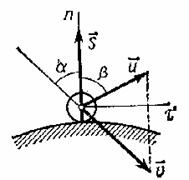
Рис.22
Коэффициент восстановления в данном случае равен
отношению модулей 
и 
, так как удар происходит только по направлению нормали к
поверхности (трением пренебрегаем). Тогда с учетом знаков проекций получим 
. В результате окончательно имеем:
.
Если величины 
и известны, то из
полученных уравнений можно найти модуль и направление скорости и ударный импульс . В частности, замечая, что 
и 
, из первого равенства получим
,
откуда 
.
Так как 
, то 
, то есть угол падения всегда меньше угла отражения.
В заключении рассмотрим случай
действия ударной силы на твердое тело, вращающееся вокруг неподвижной оси . Допустим, что на это тело в течении весьма короткого
времени действует ударная сила
,то есть к телу приложен удар
.
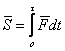(50)
Выясним, как изменится под влиянием этого удара
угловая скорость тела. Обозначив угловую скорость тела в начале и в конце удара
соответственно через 
и , и, опуская выкладки, получим
,
(51)
где 
-момент удара относительно оси вращения; 
-момент тела относительно оси вращения .
Из (51) следует, что изменение угловой скорости
твердого тела, вращающегося вокруг неподвижной оси, вызываемое приложенным к
нему ударом, равно моменту этого удара относительно оси вращения, разделенному
на момент инерции тела относительно той же оси.
Рассмотрим несколько примеров.
Пример 14. К однородному
прямолинейному стержню 
, который может вращаться на шарнире вокруг горизонтальной
оси , приложен в его середине удар , перпендикулярный к оси вращения и к направлению стержня.
Предполагая, что в начале удара стержень находится в покое, определить его
угловую скорость в конце удара, а также модуль и направление ударного импульса,
который передается при этом на шарнир . Масса стержня равна (рис.23).
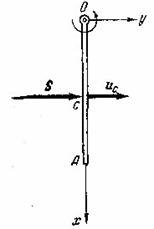
Рис.23
Решение.
Искомую угловую скорость найдем по формуле (51), в которой согласно условию
задачи нужно принять 
.
,
где 
.
Тогда для угловой скорости получим
.
Обозначим ударный импульс реакции
шарнира через 
, а скорость центра тяжести стержня в конце удара –
через 
. Эта скорость направлена перпендикулярно к стержню и по
модулю равна 
.
Учитывая, что скорость центра тяжести стержня в начале
удара равна нулю, а также, что изменение проекции на какую-нибудь ось количества движения центра масс тела равно сумме проекций на
ту же ось внешних ударов, приложенных к телу, получим
а)
; б) 
.
Из уравнения (б) получим
.
Так как , то 
.
Знак минус в значении 
указывает на то, что
удар направлен по оси 
влево. Удар,
передающийся на шарнир, будет равен по модулю 
, но направлен в противоположную сторону, то есть по оси вправо.
Пример 15. Стальной шар массы 
падает с высоты 
на стальную плиту.
Коэффициент восстановления при ударе равен 
, а время удара 
. Определить ударный импульс, а также среднюю величину
ударной реакции.
Решение.
Скорость шара в начале удара определится по формуле
.
Тогда скорость шара в конце удара по формуле (12)
будет равна
.
Величина ударного импульса определится по формуле (13)
.
Так как время удара известно, то средняя величина ударной
реакции будет равна
.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
