Главная
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ
РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ
Кинематика точки
В задачах данного раздела определяются координаты, скорость,
ускорение точки в любой назначенный момент времени при различных способах
задания движения. Из всех способов задания движения точки
наибольшее распространение получили координатный и естественный способы.
Рассмотрим вначале координатный способ задания
движения точки. Положение в пространстве движущейся точки определяется тремя
координатами в декартовой системе координат. Эти координаты задаются как
функции времени:
![]() ;
; ![]() ;
; ![]() .
(1)
.
(1)
Зависимости (1) называются уравнениями движения точки
в декартовых координатах.
Если движение точки происходит в плоскости ху, то задаются
только два уравнения движения:
![]() ;
; ![]() .
.
При прямолинейном движении точки достаточно задать
одно уравнение движения:
![]() .
.
если принять, что ось х совпадает с
прямой, по которой движется точка.
Скорость точки представляет собой вектор,
характеризующий быстроту и направление движения точки в данный момент времени.
При задании движения точки уравнениями (1) проекции
скорости на оси декартовых координат равны:
![]() ;
; ![]() ;
; ![]() .
.
Модуль скорости
![]() .
(2)
.
(2)
Направление скорости определяется направляющими
косинусами:
![]()
![]()
![]()
Если движение точки задается в плоскости ху, то ![]() ;
; ![]()
![]() ;
;
![]()
![]()
При прямолинейном движении по оси х:
![]() ;
; ![]() .
.
Характеристикой быстроты изменения скорости является
ускорение а. Ускорение точки равно производной от вектора скорости по
времени:
![]() .
.
При задании движения точки уравнениями (1) проекции
ускорения на координатные оси равны:
![]() ;
; ![]() ;
; ![]() .
.
Модуль ускорения:
![]() .
(3)
.
(3)
Направление ускорения определяется направляющими
косинусами
![]()
![]()
![]()
Если движение точки задается в плоскости ху, то ![]() ;
; ![]() ;
;
![]() ;
;
![]()
![]()
При прямолинейном движении по оси х
![]() ;
; ![]() .
.
Далее рассмотрим естественный способ задания движения
точки.
Считается, что движение точки задано естественным
способом, если указаны ее траектория и закон изменения криволинейной координаты
![]() . Уравнение
. Уравнение ![]() называется законом движения точки по
траектории. При этом на траектории указывается начало отсчета, а также
положительное направление отсчета координаты s в виде стрелки
называется законом движения точки по
траектории. При этом на траектории указывается начало отсчета, а также
положительное направление отсчета координаты s в виде стрелки ![]() .
.
Модуль скорости точки определяется по формуле
![]() .
(4)
.
(4)
Вектор скорости V
направлен по касательной к траектории в сторону стрелки ![]() , если
, если ![]() , и в противоположную сторону, если
, и в противоположную сторону, если ![]() .
.
Ускорение точки определяется как векторная сумма
касательного и нормального ускорений точки:
![]() .
.
Модуль касательного ускорения определяется по формуле
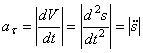 .
(5)
.
(5)
Вектор касательного ускорения ![]() направлен по
касательной к траектории в сторону стрелки
направлен по
касательной к траектории в сторону стрелки ![]() , если
, если ![]() , и в противоположную, если
, и в противоположную, если ![]() .
.
Модуль нормального ускорения определяется по формуле
![]() ,
(6)
,
(6)
где ![]() – радиус кривизны
траектории в данной точке.
– радиус кривизны
траектории в данной точке.
Вектор нормального ускорения ![]() всегда направлен по
главной нормали в сторону центра кривизны траектории.
всегда направлен по
главной нормали в сторону центра кривизны траектории.
Модуль полного ускорения
![]() .
(7)
.
(7)
Если движение точки задано координатным способом, то
можно определить параметры движения, характерные для естественного способа
задания движения.
Так можно, например, по уравнениям движения точки (1)
найти уравнение ее траектории в форме зависимости между координатами. Для этого
надо из уравнений движения исключить время t. Затем можно найти закон
движения точки по траектории ![]() , используя формулу (4). Из этой формулы следует, что
, используя формулу (4). Из этой формулы следует, что ![]() ; с учетом формулы (2) имеем
; с учетом формулы (2) имеем ![]() и
и ![]() .
(8)
.
(8)
В законе движения (8) за начало отсчета координаты s принимается
начальное положение точки, когда ![]() . Знак “плюс” или
“минус” перед интегралом ставится в зависимости от выбора положительного
направления отсчета координаты s: если движение точки начинается в сторону стрелки
. Знак “плюс” или
“минус” перед интегралом ставится в зависимости от выбора положительного
направления отсчета координаты s: если движение точки начинается в сторону стрелки ![]() , то следует брать знак “плюс”, в противном случае – знак
“минус”.
, то следует брать знак “плюс”, в противном случае – знак
“минус”.
Рассмотрим случай, когда движение точки задается в
полярных координатах. Пусть точка М
движется все время в одной и той же плоскости. Тогда ее положение можно определить полярными
координатами ![]() и
и ![]() (рис.1)
(рис.1)
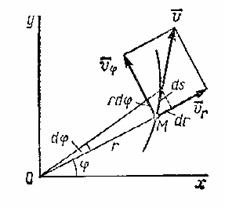
Рис.1
При движении точки ![]() эти координаты с
течением времени изменяются. Следовательно, закон движения точки в полярных
координатах будет задаваться уравнениями
эти координаты с
течением времени изменяются. Следовательно, закон движения точки в полярных
координатах будет задаваться уравнениями
![]() ,
, ![]() .
.
Скорость точки ![]() численно равна
отношению элементарного перемещения
численно равна
отношению элементарного перемещения ![]() к промежутку времени
к промежутку времени ![]() , то есть
, то есть ![]() /
/![]() . В данном случае перемещение
. В данном случае перемещение ![]() геометрически
слагается из радиального перемещения, численно равного
геометрически
слагается из радиального перемещения, численно равного ![]() , и поперечного перемещения, перпендикулярного радиусу
, и поперечного перемещения, перпендикулярного радиусу ![]() и численно равного
и численно равного ![]() . Следовательно, сама скорость
. Следовательно, сама скорость ![]() будет геометрически
складываться из радиальной скорости
будет геометрически
складываться из радиальной скорости ![]() и поперечной (трансверсальной) скорости
и поперечной (трансверсальной) скорости ![]() , численно равных
, численно равных
![]() ,
, ![]() . (9)
. (9)
Так как ![]() и
и ![]() взаимно
перпендикулярны, то модуль скорости точки
взаимно
перпендикулярны, то модуль скорости точки ![]() определится по формуле
определится по формуле
![]() .
(10)
.
(10)
Формулы (9) и (10) определяют скорость точки в
полярных координатах при плоском движении.
Ниже приводятся (без вывода) формулы для определения
проекций ускорения ![]() на радиальное и трансверсальное направления, а также для определения его
модуля
на радиальное и трансверсальное направления, а также для определения его
модуля
![]() ,
(11)
,
(11)
![]() .
.
Рассмотрим примеры решения задач.
Пример 1. Точка ![]() движется по эллипсу
так, что угловая скорость радиуса-вектора
движется по эллипсу
так, что угловая скорость радиуса-вектора ![]() , соединяющего точку
, соединяющего точку ![]() с центром эллипса,
постоянна и равна
с центром эллипса,
постоянна и равна ![]() .
Определить скорость этой точки.
.
Определить скорость этой точки.
Решение.
Выразим декартовы координаты точки ![]() через полярные
координаты
через полярные
координаты ![]() и
и ![]() (рис.2).
(рис.2).
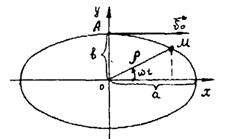
Рис.2
![]() где
где ![]() .
.
Подставив эти значения в уравнение эллипса, получим
![]() .
.
Из последнего равенства для радиуса-вектора
имеем
![]() .
.
Воспользовавшись формулами (1) и (2), найдем
радиальную и трансверсальную составляющие скорости
![]() ,
,
![]() ,
,
![]() .
.
Рассмотрим методику решения задач, в которых движение
точки задано координатным способом. Уравнения (1) определяются либо из
геометрических условий, либо в результате интегрирования дифференциальных
уравнений движения точки. Интегрирование дифференциальных уравнений движения
точки рассматривается в разделе “Динамика точки”. Получение уравнений (1) с
использованием геометрии движения рассмотрим на примере исследования
движения точки обода колеса.
Пример 2. Найти уравнения движения точки М обода колеса радиуса R
вагона, который движется по прямолинейному участку пути со скоростью V. Колесо катится без скольжения. Точка М в начальный момент движения соприкасалась
с рельсом, т.е. занимала положение М0 (рис. 3).
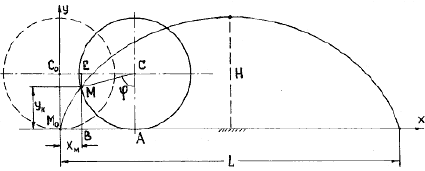
Рис. 3
Решение. Изобразим на расчетной схеме (рис.3) оси
координат х
и у, начало координат поместим в
начальное положение точки М0.
Рассмотрим два положения колеса: в начальный момент t = 0 и в текущий момент времени t.
Отметим положение точки М на ободе колеса и положение центра С колеса в момент t, координаты точки: ![]() ,
, ![]() .
.
Расстояние от центра колеса до рельса остается
постоянным и равным R; это значит,
что центр C колеса движется по
прямой, параллельной оси х. За время t центр колеса переместится на расстояние
![]() (закон равномерного
движения точки C), одновременно
колесо повернется на угол
(закон равномерного
движения точки C), одновременно
колесо повернется на угол ![]() .
.
Чтобы получить уравнения движения точки М, надо координаты этой точки представить
как функции времени.
Из расчетной схемы (рис.3) видно, что
![]() ,
, ![]()
или
![]() ,
, ![]() .
.
Из треугольника МЕС имеем;
![]() ,
,
![]() ,
,
Тогда
![]() ,
, ![]() . (12)
. (12)
Найдем зависимость угла ![]() от времени t: так как колесо
катится без скольжения, то длина дуги АМ
окружности обода колеса (рис.3) равна длине отрезка М0А.
от времени t: так как колесо
катится без скольжения, то длина дуги АМ
окружности обода колеса (рис.3) равна длине отрезка М0А.
При
этом ![]() ,
,
но
длина дуги АМ равна также
произведению радиуса R на центральный угол ![]() ; поэтому
; поэтому ![]() , отсюда
, отсюда ![]() .
.
Теперь уравнения (12) будут иметь вид
![]()
![]()
Полученные уравнения представляют собой уравнения
движения точки М. В аналитической
геометрии показано, что это параметрические уравнения циклоиды (параметром в
данном случае является время t). Таким образом, траектория точки обода колеса,
движущегося по прямолинейному участку пути без проскальзывания, является циклоидой.
Длина одной ветви циклоиды L (рис. 3)
равна ![]() , высота –
, высота – ![]() .
.
Пример 3. Даны уравнения движения точки:
![]()
![]() (где x, y - в метрах,
t - в секундах).
(13)
(где x, y - в метрах,
t - в секундах).
(13)
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси
координат.
4. Найти закон движения точки по траектории ![]() , принимая за начало отсчета расстояний начальное положение
точки.
, принимая за начало отсчета расстояний начальное положение
точки.
5. Построить график движения точки.
Решение.
1. Для получения уравнения траектории вида ![]() исключим из уравнений
движения (13) время t:
из первого уравнения системы (13) найдем
исключим из уравнений
движения (13) время t:
из первого уравнения системы (13) найдем
![]()
подставляя это выражение во второе уравнение той же
системы, получим уравнение траектории
![]() .
.
Это – уравнение прямой линии. Для построения прямой
представим ее уравнение в отрезках
![]() ,
,
где а – отрезок, отсекаемый прямой на оси х, b – отрезок, отсекаемый прямой на оси у.
В данном случае а =
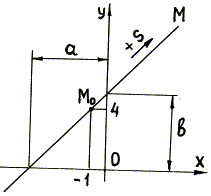
Рис. 4
2. Для определения положения точки в начальный момент
времени необходимо подставить значение t = 0 в уравнения
движения (13)
![]() м;
м;
![]() м.
м.
Точка при t = 0 занимает положение М0(-1;4).
3. В момент пересечения точкой оси у координата
х равна нулю, а первое уравнение системы
(13) примет вид:
![]() .
.
Отсюда
![]()
![]()
![]()
где n = 0, 1, 2 …
В момент пересечения точкой оси х координата у равна нулю, а второе уравнение системы
(13) примет вид:
![]() или
или ![]() .
.
Но косинус не может быть больше 1. Следовательно,
точка не пересекает ось х (см. об этом также п. 4 решения задачи).
4. Для определения закона движения точки по траектории
воспользуемся формулой (8). За начало отсчета координаты s примем начальное положение
точки М0.
Подставляя в уравнения (13) значения t > 0, видим,
что с выходом из начального положения М0 координаты точки х и у увеличиваются. Это
направление движения точки примем за положительное направление отсчета
координаты s
(см. стрелку ![]() на рис. 4), а в
формуле (8) оставим знак “плюс”:
на рис. 4), а в
формуле (8) оставим знак “плюс”:
![]() .
.
Учитывая, что
![]()
![]()
получим
![]()
или
![]() .
(14)
.
(14)
Из закона (14) следует, что координата s не может быть
отрицательной, т.е. точка движется по полупрямой М0М (рис.4) и ось х не пересекает (см. по этому поводу п. 3 решения примера).
5. График движения точки – это графическое
представление зависимости расстояния s от времени t. Для построения такого графика по оси абсцисс откладывают
последовательные значения времени t, а по оси ординат – соответствующие им значения расстояния
s.
Построенные точки соединяют плавной линией. График зависимости (14) можно
построить быстрее, если воспользоваться известным графиком косинуса. Для этого
вначале построим график функции ![]() (штриховая линия на
рис. 5), затем этот график сместим вдоль оси s на величину
(штриховая линия на
рис. 5), затем этот график сместим вдоль оси s на величину ![]() м.
м.
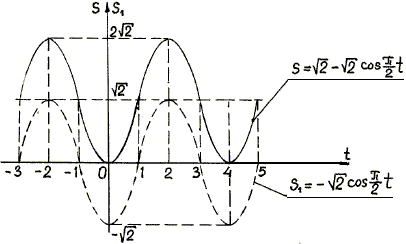
Рис.5
Пример 4. Даны уравнения движения точки:
![]()
![]() (где x, y - в сантиметрах, t - в
секундах).
(15)
(где x, y - в сантиметрах, t - в
секундах).
(15)
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на ее
траектории.
3. Найти закон движения точки по траектории ![]() ,
принимая за начало отсчета расстояний начальное положение точки.
,
принимая за начало отсчета расстояний начальное положение точки.
4. Определить время T прохождения точкой полной
окружности.
Решение.
1. Чтобы найти уравнение траектории точки необходимо
из уравнений движения (15) исключить время t. Для этого уравнения движения
(15) разрешим относительно ![]() и
и ![]() и возведем полученные
результаты в квадрат
и возведем полученные
результаты в квадрат
![]()
![]()
сложим эти уравнения и после
преобразования получим
![]() .
.
Это уравнение окружности радиуса R =
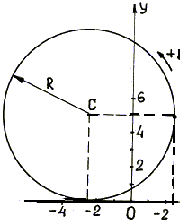
Рис. 6
2. Для определения начального положения точки подставим
значение времени ![]() в уравнения (15)
в уравнения (15)
![]() см;
см; ![]() см;
см;
Точка при ![]() занимает положение М0(2,5;
5).
занимает положение М0(2,5;
5).
3. Для определения закона движения точки по траектории
воспользуемся формулой (8). За начало отсчета координаты s
примем точку М0.
Из системы уравнений (18) видно, что с увеличением времени t от нуля x уменьшается, а y увеличивается.
Такое возможно, если после выхода из начального положения
точка будет двигаться по окружности против часовой стрелки. Это направление
движения точки примем за положительное направление отсчета координаты s (см.
стрелку ![]() на рис. 6), а в формуле (8) перед интегралом
оставим знак “плюс”:
на рис. 6), а в формуле (8) перед интегралом
оставим знак “плюс”:
![]() ,
где
,
где ![]()
![]()
Отсюда
![]()
![]() (16)
(16)
4. Определим время Т
прохождения точкой полной окружности. Т
– время, по истечении которого s в формуле (16) станет
равным длине окружности ![]() :
:
![]()
Отсюда Т=4/3
с.
Пример 5. Даны уравнения движения точки:
![]() (где x, y - в метрах,
t - в секундах).
(17)
(где x, y - в метрах,
t - в секундах).
(17)
1. Определить уравнение траектории точки.
2. Определить скорость и ускорение точки при t = 0 и t = 1 с.
3. Построить траекторию и указать полученные векторы
скорости и ускорения на чертеже.
Решение:
1. Уравнение траектории получается подстановкой в первое
уравнение системы (17) величины ![]() , полученной из второго уравнения этой системы:
, полученной из второго уравнения этой системы:
![]() (18)
(18)
2. Модуль скорости точки определяется по формуле
![]() , где
, где ![]() ,
, ![]() – проекции вектора скорости на координатные оси. Для
заданного движения (17) имеем
– проекции вектора скорости на координатные оси. Для
заданного движения (17) имеем
![]()
![]() м/c.
м/c.
При t = 0:
![]()
![]() м/c.
м/c.
Модуль
скорости ![]() = 1 м/c.
= 1 м/c.
При t = 1 сек.:
![]()
![]() м/c.
м/c.
Модуль
скорости ![]() = 4,82 м/с.
= 4,82 м/с.
Модуль ускорения точки определяется по формуле ![]() ,
где
,
где ![]() ,
, ![]() – проекции вектора
ускорения на координатные оси. Для заданного движения (17) имеем
– проекции вектора
ускорения на координатные оси. Для заданного движения (17) имеем
![]()
![]() .
.
При t = 0:
![]()
![]() .
.
Модуль
ускорения ![]() = 7,4 м/с2.
= 7,4 м/с2.
При
t = 1 сек.: ![]()
![]() .
.
Модуль
ускорения ![]() = 0.
= 0.
3. Траектория точки (18) представляет собой косинусоиду.
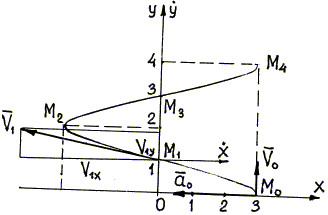
Рис.7
Для построения траектории найдем по уравнению (18)
пять точек, задавшись пятью значениями у:
у = 0, 1, 2, 3, 4, М0(3;
0), М1(0; 1), М2(-3; 2), М3(0; 3), М4(3; 4). По этим точкам
построена траектория на рис. 7. Определим положение точки в моменты
времени t =
0 и t = 1 с, учитывая (17). При t = 0 x0 =
При t = 1 сек. x1 = 0, y1 = ![]() показано на рис. 7.
Вектор скорости
показано на рис. 7.
Вектор скорости ![]() построим следующим образом: через точку М1
проведем оси
построим следующим образом: через точку М1
проведем оси ![]() и
и ![]() , ось
, ось ![]() параллельна оси x, а ось
параллельна оси x, а ось ![]() совпадает с осью y. Вдоль этих
осей от точки М1 отложим отрезки, равные проекциям V1x и V1y (с учетом их знаков); затем построим прямоугольник,
диагональ которого есть вектор
совпадает с осью y. Вдоль этих
осей от точки М1 отложим отрезки, равные проекциям V1x и V1y (с учетом их знаков); затем построим прямоугольник,
диагональ которого есть вектор ![]() . Модуль вектора ускорения
. Модуль вектора ускорения ![]() равен модулю проекции a0x
(см. п. 2),
равен модулю проекции a0x
(см. п. 2), ![]() направлен от точки М0 в сторону, противоположную
положительному направлению оси x (cкорости
направлен от точки М0 в сторону, противоположную
положительному направлению оси x (cкорости ![]() ,
,
![]() должны совпадать с касательными к траектории соответственно в
точках М0 и М1. Вектор
должны совпадать с касательными к траектории соответственно в
точках М0 и М1. Вектор ![]() должен быть направлен
от точки М0 внутрь кривой).
должен быть направлен
от точки М0 внутрь кривой).
Пример 6. Даны уравнения движения точки:
![]() ;
; ![]() (где x, y - в метрах,
t - в секундах).
(19)
(где x, y - в метрах,
t - в секундах).
(19)
1. Определить уравнение траектории точки.
2. Определить скорость и ускорение точки при t = 1 с.
3. Построить траекторию и указать полученные векторы
скорости и ускорения на чертеже.
Решение
1. Для того чтобы получить уравнение траектории,
необходимо из уравнений движения (19) исключить время. Запишем эти уравнения в
виде
![]()
![]()
Возведем оба уравнения в квадрат, вычтем второе из
первого и получим уравнение траектории:
![]() .
(20)
.
(20)
Это уравнение равнобочной гиперболы, полуось которой b =
2. Определим проекции скорости
![]() м/с;
м/с; ![]() м/с.
м/с.
В
заданный момент времени t
= 1с, V1x = 4,68 м/с, V1у = 6,16 м/с модуль
скорости ![]() м/с.
м/с.
Определим проекции ускорения
![]() м/с2,
м/с2,
![]() м/с2 .
м/с2 .
В момент времени t = 1с, а1x =
6,16 м/с2, а1у = 4,68 м/с2
модуль ускорения ![]() м/с2.
м/с2.
3. Построим траекторию точки по уравнению (20).
Действительной осью гиперболы является ось х (рис. 8). На траектории найдем
точку М1,
соответствующую моменту времени t = 1 сек. Координаты этой точки: ![]() м;
м; ![]() м; М1 (6,16; 4,68).
м; М1 (6,16; 4,68).
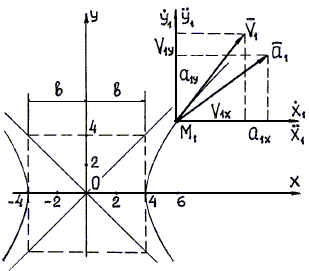
Рис. 8
Вектор скорости построим следующим образом: через
точку М1
проведем оси ![]() и
и ![]() , параллельные соответствующим осям x и y; вдоль этих осей от точки М1 отложим отрезки, равные
проекциям V1x и V1y (с учетом их
знаков). Диагональ прямоугольника, построенного на этих отрезках, есть вектор
, параллельные соответствующим осям x и y; вдоль этих осей от точки М1 отложим отрезки, равные
проекциям V1x и V1y (с учетом их
знаков). Диагональ прямоугольника, построенного на этих отрезках, есть вектор ![]() . Вектор ускорения
. Вектор ускорения ![]() строим подобным
образом: от точки М1 вдоль оси
строим подобным
образом: от точки М1 вдоль оси ![]() отложим отрезок,
равный проекции a1x, а вдоль оси
отложим отрезок,
равный проекции a1x, а вдоль оси ![]() отложим отрезок a1y.
Затем на этих отрезках строим прямоугольник, диагональ которого есть вектор
отложим отрезок a1y.
Затем на этих отрезках строим прямоугольник, диагональ которого есть вектор ![]() . Вектор скорости
. Вектор скорости ![]() должен быть направлен
по касательной к траектории в точке М1, а вектор ускорения
должен быть направлен
по касательной к траектории в точке М1, а вектор ускорения ![]() должен быть направлен
от точки М1
внутрь кривой.
должен быть направлен
от точки М1
внутрь кривой.
Пример 7. Даны уравнения движения точки М шатуна АВ
кривошипно-ползунного механизма (рис. 9):
![]() ;
; ![]() (где x, y - в метрах,
t - в секундах).
(21)
(где x, y - в метрах,
t - в секундах).
(21)
1. Определить уравнение траектории точки.
2. Определить скорость и ускорение точки в момент,
когда она пересечет прямую y =
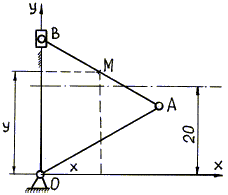
Рис. 9
Решение.
1. Чтобы определить уравнение траектории, следует
исключить время из уравнений движения (21). Учитывая, что
![]() ,
,
получим
![]()
Траектория представляет собой эллипс с полуосями
2. Определим время Т,
когда точка пересечет прямую у = ![]() ,
отсюда следует
,
отсюда следует ![]() ;
; ![]() ;
; ![]() сек.
сек.
Найдем величины скорости и
ускорения по значениям их проекций в момент времени ![]() с:
с:
![]() ;
;
![]()
Модуль скорости ![]() см/с.
см/с.
Проекции ускорения
![]()
![]()
Модуль ускорения
![]() см/с2.
см/с2.
Пример 8.
Дан закон движения точки по окружности радиуса R = 5 м:
![]() (где s в см; t в сек.).
(22)
(где s в см; t в сек.).
(22)
1. Определить скорость и ускорение точки при t = 0 и t1 = 10 с.
2. Определить моменты остановки точки.
3. Определить путь, пройденный точкой за 10 с.
Решение
1. На траектории отметим точку O – начало отсчета координаты
s и укажем положительное направление отсчета этой
координаты стрелкой ![]() (рис. 10). Отметим
положение точки в моменты времени t = 0 и t1 = 10 с. При t = 0, s0 =
(рис. 10). Отметим
положение точки в моменты времени t = 0 и t1 = 10 с. При t = 0, s0 = ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
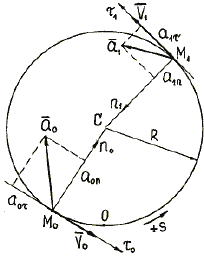
Рис. 10
Определим проекцию скорости на касательную ![]() , учитывая (22),
, учитывая (22),
![]() . (23)
. (23)
При t = 0, ![]() = 162 см/с
= 162 см/с
и t1 = 10 c, ![]() = 12 см/с.
= 12 см/с.
Теперь отложим найденные проекции скорости из точек M0 и M1 по соответствующим касательным: ![]() – по касательной
– по касательной ![]() ,
, ![]() – по касательной
– по касательной ![]() . Векторы
. Векторы ![]() и
и ![]() совпадают со своими
проекциями
совпадают со своими
проекциями ![]() и
и ![]() .
.
Определим проекции ускорения на естественные оси
координат, учитывая (22),
![]() см/с2;
см/с2; ![]()
Ускорение точки ![]() .
.
При t = 0:
![]() см/с2;
см/с2;
![]()
![]() см/с2.
см/с2.
При t1
= 10 сек.: ![]() см/с2;
см/с2;
![]()
![]() см/с2.
см/с2.
Отложим из точек М0 и М1
по естественным осям проекции ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Векторы
. Векторы ![]() ,
, ![]() изображаются
диагоналями прямоугольников, построенных на проекциях ускорений.
изображаются
диагоналями прямоугольников, построенных на проекциях ускорений.
2. Чтобы найти моменты остановки, необходимо найти
время ![]() , когда скорость
точки равна нулю. Из уравнения (23) получим
, когда скорость
точки равна нулю. Из уравнения (23) получим
![]() .
.
Решив это уравнение, будем иметь ![]() = 6 с,
= 6 с,
![]() = 9 с.
= 9 с.
3. Поскольку за 10 с точка сделала
две остановки (см. п. 2), пройденный ею путь за 10 с можно найти как сумму
пути, пройденного точкой от начального положения до первой остановки, пути,
пройденного точкой от первой до второй остановки, и пути, пройденного точкой от
второй остановки до момента времени t1
= 10 с, т.е.
![]() ,
,
где s0
=
![]() см;
см;
![]() см;
см;
![]() см.
см.
Путь, пройденный точкой за 10 сек, равен
![]() см.
см.
Пример 9.
По заданным уравнениям движения точки:
![]() ;
; ![]() (где x, y - в метрах,
t - в секундах).
(24)
(где x, y - в метрах,
t - в секундах).
(24)
найти ее касательное и нормальное ускорение, а также
радиус кривизны траектории для заданного момента времени ![]() сек.
сек.
Решение:
Заданные уравнения движения точки (24) позволяют найти
проекции скорости точки, м/с,
![]() ;
;
![]() .
.
Модуль скорости, м/с,
![]() .
(25)
.
(25)
В момент времени ![]() сек.: V1
= 2 м/с.
сек.: V1
= 2 м/с.
Проекции ускорения точки, м/с2:
![]() ;
;
![]() .
.
Модуль
полного ускорения, м/с2
![]() .
(26)
.
(26)
В момент времени ![]() сек.: a = 2
м/с2.
сек.: a = 2
м/с2.
Зная выражение скорости, как функции времени t (25),
определим модуль касательного ускорения точки, м/с2,
по формуле (5)
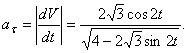 (27)
(27)
В момент ![]() сек.:
сек.: ![]() м/с2.
м/с2.
По полному ускорению (26) и касательному ускорению
(27) найдем модуль нормального ускорения точки для ![]() сек., учитывая формулу (7)
сек., учитывая формулу (7)
![]() м/с2.
м/с2.
Нормальное ускорение ![]() и радиус кривизны
траектории
и радиус кривизны
траектории ![]() связаны зависимостью
(6), из которой следует, что при
связаны зависимостью
(6), из которой следует, что при ![]() сек.:
сек.:
![]() .
.
Пример 10. Даны уравнения движения точки в плоскости xy:
![]()
![]() (где x, y -
в сантиметрах, t - в секундах).
(где x, y -
в сантиметрах, t - в секундах).
Определить уравнение траектории точки; для момента
времени t1 =1 сек. найти скорость и ускорение точки, а также ее
касательное и нормальное ускорения и радиус кривизны в соответствующей точке
траектории.
Указания.
Задача относится к кинематике точки и решается с помощью формул, по которым
определяются скорость и ускорение точки в декартовых координатах (координатный
способ задания движения точки), а также формул, по которым определяются
касательное и нормальное ускорения точки.
Решение.
1. Для определения уравнения траектории точки исключим
из заданных уравнений движения время t. Поскольку t входит в
аргументы тригонометрических функций, где один аргумент вдвое больше другого,
используем формулу
![]() или
или ![]() .
(28)
.
(28)
Из уравнения движения находим выражения
соответствующих функций и подставляем в равенство (28). Получим
![]() ,
, ![]() ,
,
следовательно,
![]() .
.
Отсюда окончательно находим следующее уравнение
траектории точки (параболы, рис. 11):
![]() .
(29)
.
(29)
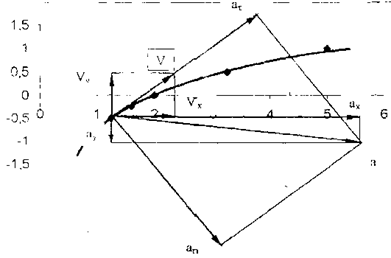
Рис.
11
2. Скорость точки найдем по ее проекциям на
координатные оси![]()
![]()
![]()
![]()
и при t =1с ![]()
![]()
![]() . (30)
. (30)
3. Аналогично найдем ускорение точки![]()
![]()
![]()
![]()
и при ![]() сек.
сек. ![]() ,
, ![]()
![]() . (31)
. (31)
4 Касательное ускорение
найдем, дифференцируя по времени равенство:
![]() .
.
Получаем![]()
![]() и
и ![]() .
(32)
.
(32)
Числовые значения всех величин, входящих в правую
часть выражения (32), определены и даются равенствами (30) и (31). Подставив в
(32) эти числа, найдем, что при ![]() сек.
сек. ![]() = 0,66 cм/с2.
= 0,66 cм/с2.
5. Нормальное ускорение точки ![]() . Подставив сюда найденные числовые значения
. Подставив сюда найденные числовые значения ![]() и
и ![]() , получим, что при
, получим, что при ![]() сек.
сек. ![]() = 0,58 cм/с2.
= 0,58 cм/с2.
6. Радиус кривизны траектории ![]() . Подставляя сюда числовые значения V
и
. Подставляя сюда числовые значения V
и ![]() ,
найдем, что при
,
найдем, что при ![]() сек.
сек. ![]() =
3,05 см.
=
3,05 см.
Ответ: V = 1,33 cм/c, ![]() = 0,88 cм/с2,
= 0,88 cм/с2,
![]() = 0,66 cм/с2,
= 0,66 cм/с2, ![]() = 0,58 cм/с2,
= 0,58 cм/с2, ![]() = 3,05 см.
= 3,05 см.
Пример
11. Точка движется по дуге
окружности радиуса R = 2 м по закону ![]() (s- в метрах, t – в секундах),
где s = AM (рис.12).
Определить скорость и ускорение точки в момент времени
(s- в метрах, t – в секундах),
где s = AM (рис.12).
Определить скорость и ускорение точки в момент времени ![]() сек.
сек.
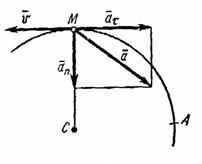
Рис.12
Решение.
Определяем скорость точки
![]()
При ![]() сек. получим
сек. получим ![]() .
.
Ускорение находим по его касательной и нормальной
составляющим ![]()
![]()
![]() .
.
При ![]() сек. получим, учтя, что
сек. получим, учтя, что ![]() м:
м:
![]() ,
,
![]() .
.
Тогда ускорение точки при ![]() сек. будет
сек. будет
![]() .
.
Пример 12. По
заданному уравнению движения точки М
![]() (где
(где ![]() - в см)
- в см)
Установить вид ее траектории и для момента ![]() сек. найти положение точки на траектории, ее
скорость и ускорение.
сек. найти положение точки на траектории, ее
скорость и ускорение.
Решение:
Определяем вид траектории движения точки М.
Движение точки М
задано векторным способом
![]() (33)
(33)
Выберем систему отсчета xoy
(рис. 13).
Построим векторы ![]() ,
, ![]() ,
, ![]() ,
подставляя время t0= 0
сек., t1= 1
сек., t2= 2 сек.
в (33)
,
подставляя время t0= 0
сек., t1= 1
сек., t2= 2 сек.
в (33)
![]()
![]() ,
,
![]() .
.
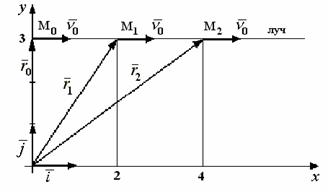
Рис. 13
Соединяя концы радиусов-векторов,
получим траекторию точки М.
Рисунок показывает, что траекторией движения является
луч, параллельный оси x,
с началом в точке М0.
Положение
точки М на траектории при ![]() сек. определяет
радиус-вектор
сек. определяет
радиус-вектор ![]() .
.
Скорость точки М
находим по формуле
![]() .
.
Величина скорости
![]() см/с
= const -
означает, что движение точки равномерное.
см/с
= const -
означает, что движение точки равномерное.
![]() - вектор скорости
- вектор скорости ![]() параллелен оси X и совпадает
с ее положительным направлением (рис.
15).
параллелен оси X и совпадает
с ее положительным направлением (рис.
15).
Ускорение точки М
![]() .
.
Ответ: точка совершает прямолинейное равномерное движение.
Пример 13. По
заданным уравнениям движения точки М
![]() ,
, ![]() (где x, y - в см)
(где x, y - в см)
установить вид ее траектории и для момента времени ![]() сек. найти положение точки на траектории, ее скорость,
ускорение.
сек. найти положение точки на траектории, ее скорость,
ускорение.
Решение:
Определяем вид траектории.
Движение точки М задано координатным способом
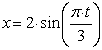 ,
, ![]() (34)
(34)
Исключая время ![]() из уравнений движения
(34), найдем вид траектории точки М в
координатной форме.
из уравнений движения
(34), найдем вид траектории точки М в
координатной форме.
Так как время ![]() входит в аргументы
тригонометрических функций синуса и косинуса, то, используя формулу
входит в аргументы
тригонометрических функций синуса и косинуса, то, используя формулу
![]() , получим
, получим
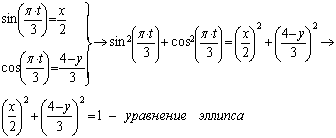
Траекторией движения точки М является эллипс (рис. 14).
Центр эллипса С имеет координаты
![]() .
.
Полуоси эллипса а=2 см, b=3 см.
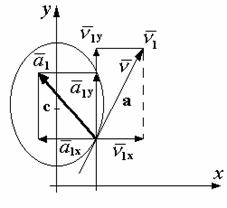

Рис.14
Определяем положение точки на траектории при ![]() сек.
сек.
Подставляя время ![]() сек. в (34), получим
сек. в (34), получим
![]() ,
,
![]() .
.
Точку с координатами ![]() ,
, ![]() обозначим на траектории через М1.
обозначим на траектории через М1.
Скорость ![]() точки М определим через ее проекции на
координатные оси.
точки М определим через ее проекции на
координатные оси.
![]() ,
, ![]() , где
, где
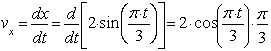 ,
,
![]() .
.
Тогда
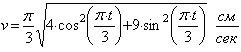 .
.
Так как величина скорости ![]() зависит от времени
зависит от времени ![]() , то движение точки неравномерное.
, то движение точки неравномерное.
При ![]() сек.
сек.
![]()
![]() ,
,
![]()
Построим на рис.14 вектор скорости точки М1.
![]() или
или ![]() .
.
В точке М1 параллельно осям x, y, в
выбранном масштабе, откладываем
![]()
![]() .
.
Вектор ![]() - диагональ
прямоугольника, построенного на
- диагональ
прямоугольника, построенного на ![]() и
и ![]() , как на сторонах.
, как на сторонах.
Контроль:
вектор скорости ![]() должен лежать на касательной,
проведенной к эллипсу в точке М1.
должен лежать на касательной,
проведенной к эллипсу в точке М1.
Ускорение ![]() точки М находим аналогично, то есть
точки М находим аналогично, то есть ![]() ,
, ![]() .
.
![]() ,
,
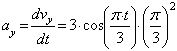 ,
,
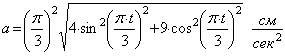 .
.
В момент времени ![]() сек.
сек.
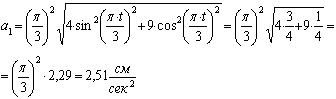
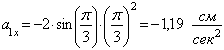 ,
,
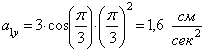 .
.
Построим на рис. 14 вектор ускорения ![]() .
.
В точке М1 параллельно осям X и Y отложим
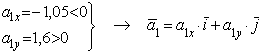 .
.
Вектор ![]() - диагональ прямоугольника, построенного на
- диагональ прямоугольника, построенного на ![]() ,
, ![]() как на сторонах.
как на сторонах.
Контроль: вектор
ускорения ![]() должен лежать в плоскости
траектории и направлен в сторону ее вогнутости.
должен лежать в плоскости
траектории и направлен в сторону ее вогнутости.
Ответ: точка
М совершает криволинейное в данный
момент ускоренное движение, т.к. угол между векторами ![]() и
и ![]() острый.
острый.
Пример 14. Даны уравнения движения точки
М в
плоскости xy:
![]() ,
, ![]() (где x, y - в сантиметрах,
(где x, y - в сантиметрах, ![]() - в секундах).
- в секундах).
Найти уравнение траектории точки М; для момента времени ![]() сек. найти положение точки на траектории, ее
скорость, полное ускорение, касательное и нормальное ускорения, а также радиус
кривизны в соответствующей точке.
сек. найти положение точки на траектории, ее
скорость, полное ускорение, касательное и нормальное ускорения, а также радиус
кривизны в соответствующей точке.
Решение:
1. Исключая время ![]() из уравнений движения
из уравнений движения
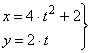 (35)
(35)
найдем уравнение траектории.
Из второго уравнения
подставляя это значение ![]() в первое уравнение,
получим
в первое уравнение,
получим
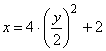 или
или ![]() – уравнение параболы.
– уравнение параболы.
Заметим, что траекторией движения является только
верхняя ветвь параболы, т.к. время t>0 и значения ![]() .
.
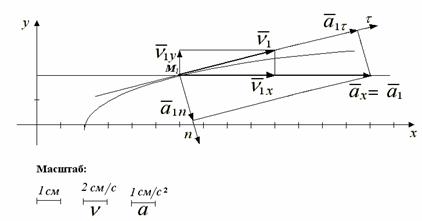
Рис.15
2. Полагая время ![]() сек., в уравнениях
(35) найдем координаты, определяющие положение точки на траектории в этот
момент времени
сек., в уравнениях
(35) найдем координаты, определяющие положение точки на траектории в этот
момент времени
![]()
![]() .
.
Точку с координатами ![]() =6,
=6, ![]() =2 на траектории обозначим М1.
=2 на траектории обозначим М1.
3. Величину скорости точки М найдем по ее проекциям на координатные оси:
![]() , где
, где
![]() ,
,
![]() .
.
Тогда
![]() .
.
Поскольку величина скорости зависит от времени ![]() , то движение точки неравномерное.
, то движение точки неравномерное.
В момент времени ![]() сек.
сек.
![]()
![]()
![]() .
.
Выберем масштаб и построим вектор скорости в положении
М1
по составляющим ![]() и
и ![]()
![]()
![]() - диагональ
прямоугольника, сторонами которого являются
- диагональ
прямоугольника, сторонами которого являются
![]() ,
, ![]() .
.
Причем, вектор скорости ![]() должен по направлению совпадать
с касательной, проведенной к траектории в точке М1.
должен по направлению совпадать
с касательной, проведенной к траектории в точке М1.
4. Модуль ускорения точки М определяем
аналогично
![]() , где
, где
![]() ,
,
![]() .
.
Полное ускорение
![]()
является постоянным во все время движения точки.
Выберем масштаб, построим вектор ускорения (рис.15):
![]() ,
, ![]() .
.
Вектор ускорения должен лежать в
плоскости траектории и направлен в сторону ее вогнутости.
5. Проведем через точку М1 (рис.15) ось ![]() вдоль касательной и
ось
вдоль касательной и
ось ![]() – вдоль нормали в
сторону вогнутости траектории.
– вдоль нормали в
сторону вогнутости траектории.
Разложим полное ускорение на составляющие вдоль этих
осей
![]() , где
, где
![]() - касательное ускорение точки М;
- касательное ускорение точки М;
![]() - нормальное ускорение точки М.
- нормальное ускорение точки М.
Из рисунка ![]() ,
, ![]()
Аналитически касательное
ускорение определяется по формуле
![]()
и характеризует изменение скорости по величине.
Если ![]() – движение ускоренное,
– движение ускоренное,
Если ![]() – движение замедленное.
– движение замедленное.
Найдем ![]()
![]()
Т.к. время t > 0, выражение ![]() , следовательно, движение точки М ускоренное.
, следовательно, движение точки М ускоренное.
В момент ![]() сек.
сек.
![]() соответствует значению
на рисунке).
соответствует значению
на рисунке).
Нормальное ускорение характеризует изменение скорости
по направлению. В случае криволинейного движения, оно всегда существует и
определяется по формуле
![]() , где
, где ![]() - радиус кривизны траектории в соответствующей точке.
- радиус кривизны траектории в соответствующей точке.
Т.к. радиус кривизны параболы в точке М1
не известен, то величину нормального ускорения можно определить следующим образом:
![]()
В момент ![]() сек.
сек.
![]() соответствует значению на рисунке).
соответствует значению на рисунке).
Радиус кривизны параболы в точке М1
найдем из выражения
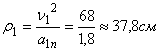
Заметим, что совпадение величин ![]() ,
, ![]() найденных на рис.15 с
их значениями полученными аналитически подтверждает, что задача решена верно.
найденных на рис.15 с
их значениями полученными аналитически подтверждает, что задача решена верно.
Ответ: точка М совершает криволинейное
ускоренное движение, т.к. вектор касательного ускорения во все время движения
совпадает с направлением вектора скорости.
Пример 15. Точка М
движется по окружности радиуса R = 2м
по закону ![]() м.
м.
Найти скорость ![]() и ускорение
и ускорение ![]() точки М в момент времени
точки М в момент времени ![]() сек. Установить вид
движения точки М в этот момент
времени.
сек. Установить вид
движения точки М в этот момент
времени.
Решение:
Траектория движения точки М – окружность радиуса ![]() 2м.
2м.
Воспользуемся естественным способом задания движения
точки. Выберем на траектории какую-нибудь неподвижную точку О (рис.16), которую примем за начало
отсчета, и укажем на траектории положительное и отрицательное направления
отсчета. Положение точки М на
траектории определим дуговой координатой S,
которая с течением времени будет изменяться по закону
![]() (36)
(36)
1) Установим, где находится точка М на окружности в момент времени t1.
Полагая в уравнении (36) ![]() сек., получим
сек., получим ![]() м.
м.
Тогда
![]() .
.
Знак плюс означает, что угол ![]() надо отложить в
сторону положительного отсчета S. На
траектории получим точку М1. Через точку М1 проведем ось
надо отложить в
сторону положительного отсчета S. На
траектории получим точку М1. Через точку М1 проведем ось ![]() по касательной к
траектории в сторону положительного отсчета S;
ось
по касательной к
траектории в сторону положительного отсчета S;
ось ![]() - по нормали к
траектории и направленную в сторону вогнутости траектории.
- по нормали к
траектории и направленную в сторону вогнутости траектории.
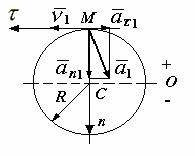
Рис.16
2) Определим скорость точки М.
![]() .
.
В момент ![]() сек.
сек.
![]() .
.
Знак плюс означает, что ![]() откладываем вдоль
касательной влево.
откладываем вдоль
касательной влево.
3) Ускорение точки М
находим через его касательную ![]() и нормальную
и нормальную ![]() составляющие.
составляющие.
Касательное ускорение
![]() .
.
Нормальное ускорение ![]() ,
где
,
где ![]() - радиус кривизны окружности,
- радиус кривизны окружности,
![]() м.
м.
В момент времени ![]() сек.
сек.
![]() .
.
Знак минус означает, что ![]() откладываем вдоль
касательной вправо, в сторону отрицательного отсчета S.
откладываем вдоль
касательной вправо, в сторону отрицательного отсчета S.
![]() м/c2.
м/c2.
![]() откладываем вдоль
нормали, в сторону вогнутости траектории.
откладываем вдоль
нормали, в сторону вогнутости траектории.
Ускорение точки М
![]() ,
,
![]() м/c2.
м/c2.
Ответ: точка
М совершает криволинейное, в данный
момент замедленное движение, т.к. вектор скорости ![]() и касательное
ускорение
и касательное
ускорение ![]() не совпадают по
направлению.
не совпадают по
направлению.
Пример 16. По заданным уравнениям
движения точки М установить вид ее
траектории и для момента времени ![]() сек. найти положение точки
на траектории, ее скорость, полное, касательное и нормальное ускорения, а также
радиус кривизны траектории в соответствующей точке.
сек. найти положение точки
на траектории, ее скорость, полное, касательное и нормальное ускорения, а также
радиус кривизны траектории в соответствующей точке.
![]() ;
; ![]() .
.
Решение.
Исходные данные в см и сек:
![]() ;
;
![]() ; (37)
; (37)
t1 = 0,5 сек.
Уравнения движения (37) являются
параметрическими уравнениями траектории точки М. Чтобы получить уравнение траектории в обычной координатной форме,
исключим время t из уравнений движения. Тогда
![]() (38)
(38)
Это уравнение параболы.
Для определения скорости точки
находим проекции скорости на оси координат:
![]() см/с;
см/с; ![]() см/с.
см/с.
Модуль скорости точки
![]() .
(39)
.
(39)
Аналогично проекции ускорения точки
![]() см/с2;
см/с2; ![]() .
.
Модуль ускорения точки
![]() см/с2.
см/с2.
Касательное ускорение находим путем дифференцирования
модуля скорости (39)
![]()
![]()
При t = 0,5 c
x = -2×0,52 + 3 = 2,5 см, y
= -5×0,5 = -2,5 см.
Vx = -4×0,5
=-2 см/с, Vy = -5 см/с,
V = 5,38 см/с.
ax = -4 см/с2, ay
= 0, a = 4 см/с2
![]() см/с2
см/с2
Модуль касательного ускорения
![]() = 1,487 см/с2
= 1,487 см/с2
Знак “+” при ![]() показывает, что
движение точки ускоренное и, следовательно, направления
показывает, что
движение точки ускоренное и, следовательно, направления ![]() совпадают.
совпадают.
Нормальное
ускорение точки:
![]() см/с2.
см/с2.
Радиус кривизны траектории в той
точке, где при t = 0,5 с находится
точка М:
![]() см.
см.
Пользуясь уравнением (38), строим траекторию
(рис.17) и показываем на ней положение точки М в заданный момент времени. Вектор ![]() строим по составляющим
строим по составляющим
![]() и
и ![]() , причем он направлен по касательной к траектории точки.
Вектор
, причем он направлен по касательной к траектории точки.
Вектор ![]() находим как по
составляющим
находим как по
составляющим ![]() и
и
![]() ,
так и по
,
так и по ![]() и
и ![]() .
.
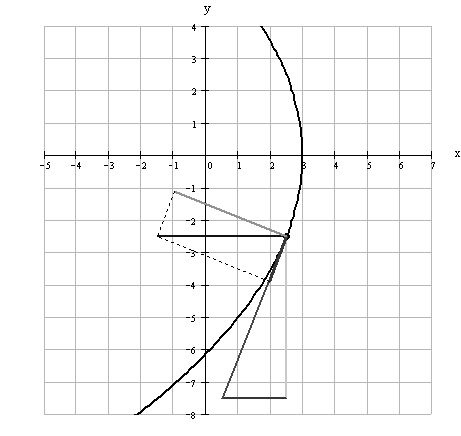
Рис. 17
Пример 17. По дуге радиусом r=1200
м движется поезд (рис.18), его скорость в начале движения по дуге составляет ![]() =60 км/ч. После того как поезд прошел расстояние 800 м, его
скорость уменьшилась до
=60 км/ч. После того как поезд прошел расстояние 800 м, его
скорость уменьшилась до
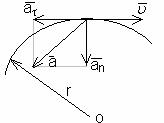
Рис.18
Указание.
В задаче рассматривается равнопеременное движение точки. Следует учесть, что
при использовании уравнения равнопеременного движения точки ![]() по криволинейной
траектории кроме касательного ускорения
по криволинейной
траектории кроме касательного ускорения ![]() , у точки возникает нормальное тангенциальное ускорение
, у точки возникает нормальное тангенциальное ускорение ![]() , направленное по радиусу кривизны траектории к ее центру.
, направленное по радиусу кривизны траектории к ее центру.
Решение.
Определим касательное ускорение из уравнений:
![]() ,
, ![]()
Из второго уравнения
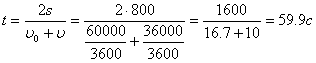
Из первого уравнения
![]()
Так как равномерно замедленное, то касательное
ускорение в течении всего времени движения постоянно.
Найдем нормальное ускорение:
в начале движения
![]() = 16,72/1200=0,23 м/с2,
= 16,72/1200=0,23 м/с2,
в конце движения
![]() = 102/1200=0,08м/с2.
= 102/1200=0,08м/с2.
Полное ускорение:
в начале движения ![]()
в конце движения ![]()
Пример 18. Уравнение движения тела имеет вид ![]() . Определить ускорение a0 и
скорость тела v0 в начальный
момент времени, а также среднее ускорение aср за первые 5 секунд движения.
. Определить ускорение a0 и
скорость тела v0 в начальный
момент времени, а также среднее ускорение aср за первые 5 секунд движения.
Решение.
Поскольку ![]() , то
, то
![]() . (1)
. (1)
Далее, из ![]() получим
получим
![]() . (2)
. (2)
Подставив в (1) и (2) t=0, найдем v0=5 м/с, а0=0
м/с2.
Среднее ускорение находим по определению ![]() , то есть
, то есть ![]() , где скорость в момент времени t=5c находим из (1):
, где скорость в момент времени t=5c находим из (1): ![]() м/с.
Окончательно
м/с.
Окончательно ![]()
Пример 19. Начальная скорость брошенного под некоторым углом к
горизонту камня равна 10 м/с, а спустя 0,5 с скорость
камня равна 7 м/с. На какую максимальную высоту
над начальным уровнем поднимется камень?
Решение.
Максимальная высота подъема тела, брошенного под углом
к горизонту, может быть найдена из общей формулы пути при равнопеременном
движении в проекции на вертикальную ось
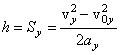
с учетом, что в наивысшей точке траектории отсутствует
вертикальная составляющая скорости vy=0, а ![]() :
:
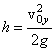 . (1)
. (1)
Неизвестную проекцию начальной скорости на
вертикальную ось v0y
можно найти из формулы скорости при равнопеременном движении ![]() в проекции на вертикальную ось:
в проекции на вертикальную ось:
![]() (2)
(2)
и теоремы
Пифагора для полной скорости в начальный момент времени и спустя время t после начала
движения:
![]() , (3)
, (3)
![]() . (4)
. (4)
Здесь учтено, что проекция скорости на горизонтальную
ось ![]() не изменяется, так как
не изменяется, так как
![]() . Вычтем почленно (4) из (3), и с
учетом (2) получим:
. Вычтем почленно (4) из (3), и с
учетом (2) получим:
![]() . (5)
. (5)
Из (5) находим v0y:
![]() .
.
Далее из (1) находим высоту подъема:
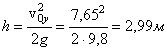 .
.
Пример 20. Определить тангенциальное ![]() , нормальное an и
полное ускорение a точки
окружности диска для момента времени t=10 с от
начала движения, если радиус окружности R=0,2 м, а угол между осью ОХ и радиус-вектором точки
изменяется по закону:
, нормальное an и
полное ускорение a точки
окружности диска для момента времени t=10 с от
начала движения, если радиус окружности R=0,2 м, а угол между осью ОХ и радиус-вектором точки
изменяется по закону: ![]() .
.
Решение.
По формулам ![]() и
и ![]() находим угловую
скорость и угловое ускорение точки:
находим угловую
скорость и угловое ускорение точки: ![]() ,
, ![]() . Из формулы связи углового и линейного тангенциального
ускорения найдем:
. Из формулы связи углового и линейного тангенциального
ускорения найдем:
![]() м/с2.
м/с2.
Нормальное ускорение найдем из формулы ![]() , где скорость
, где скорость
![]() м/с;
м/с; ![]()
Теперь находим полное ускорение: ![]() .
.
Пример 21. Даны
уравнения движения точки в плоскости ху:
![]() ,
, ![]()
(х, у - в метрах, t
- в секундах).
Определить уравнение траектории точки. Для момента
времени t1 = 1 с найти скорость и ускорение точки,
а также ее касательное и нормальное ускорения и радиус кривизны в
соответствующей точке траектории.
Решение.
1.Для определения траектории исключим из заданных
уравнений движения время t, воспользовавшись подстановкой:
![]()
![]()
Из полученного выражения следует, что траекторией
движения точки является парабола с нисходящими ветвями и осью, параллельной оси
у; вершина параболы находится в точке с координатами х = -3 м, у = 0.
2.Найдем проекции вектора скорости на оси координат:
![]()
![]()
Подставив t1
= 1 с в полученные выражения, находим
![]()
![]()
Скорость точки в момент времени t1 = 1 с
![]()
Найдем проекции вектора ускорения:
![]()
![]()
Для момента времени t1 = 1 с
![]()
![]()
![]() м/с2.
м/с2.
Касательное ускорение найдем по формуле
![]() м/с2.
м/с2.
Нормальное ускорение
![]() м/с2.
м/с2.
Вычислим радиус кривизны траектории в том месте, где
находится точка в момент времени t1
= 1 с:
![]() м.
м.
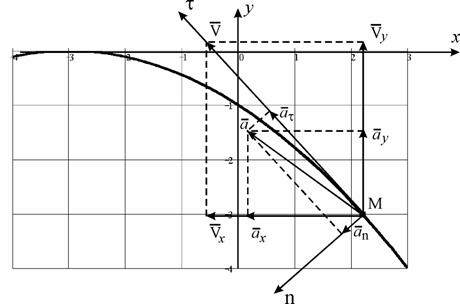
Рис.19
3.Пользуясь уравнением траектории, вычерчиваем
параболу (рис. 19) и показываем на ней точку М в заданный момент времени по ее координатам. Вектор скорости ![]() строим по составляющим
строим по составляющим
![]() и
и ![]() ; он должен быть направлен по касательной к траектории.
Вектор ускорения
; он должен быть направлен по касательной к траектории.
Вектор ускорения ![]() находим по его составляющим
находим по его составляющим ![]() и
и ![]() . Далее найденный вектор раскладываем на направления
касательной и нормали и получаем векторы касательного
. Далее найденный вектор раскладываем на направления
касательной и нормали и получаем векторы касательного ![]() и нормального
и нормального ![]() ускорений. Полученные
таким образом значения
ускорений. Полученные
таким образом значения ![]() и
и ![]() должны совпасть с
результатами их подсчета по формулам.
должны совпасть с
результатами их подсчета по формулам.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов