Главная

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

4. Кинематика сложного движения точки

4.1. Основные понятия и определения

С исследованием движения точки мы уже ознакомились при изучении раздела “Кинематика точки”. Тогда предполагалось, что точка движется по заданному закону относительно неподвижного тела (или относительно неподвижной системы отсчета).

Если же точка движется по заданному закону относительно тела, а тело, в свою очередь, перемещается относительно неподвижной системы отсчета, то движение точки относительно неподвижной системы отсчета называется сложным или составным: оно складывается из движения точки по телу и движения вместе с этим телом.

Например, мяч, катящийся по палубе плывущего вдоль берега теплохода, совершает относительно берега сложное движение, которое состоит из качения по палубе и движения вместе с палубой (теплоходом). Сложное движение относительно платформы совершает человек, идущий внутри вагона движущегося поезда. Шарик, вылетающий из вращающейся трубки, совершает сложное движение относительно неподвижной стойки. Под стойкой здесь и в дальнейшем понимается некоторое неподвижное основание.

Рассмотрим движение точки М (рис. 65) по траектории 1–1 внутри тела А, которое, в свою очередь, движется относительно неподвижного тела В (стойки). Движение точки М по отношению к телу В есть сложное движение.

Система координатных осей О₁х₁у₁z₁, связанная с движущимся телом А, называется подвижной системой

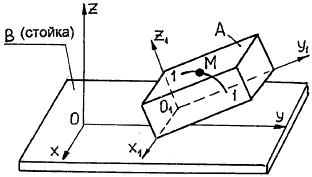
Рис. 65

Система осей Охуz, связанная с неподвижным телом В (стойкой), называется неподвижной системой отсчета.

Движение точки M относительно тела A (или относительно О₁х₁у₁z₁) по траектории 1–1 называется относительным движением точки М. Скорость и ускорение точки М в этом движении есть относительная скорость и относительное ускорение точки М, их обозначают и соответственно.

Движение тела А (или системы О₁х₁у₁z₁) относительно стойки (относительно Охуz) называется переносным движением. Переносной скоростью (ускорением) точки М называется скорость (ускорение) точки тела А, с которой в данный момент совпадает движущаяся по телу точка М. Поясним это определение.

В каждый момент времени точка М совпадает с некоторой точкой М' тела А (рис. 66). Скорость (ускорение) точки М' и есть переносная скорость (ускорение) точки М. Переносную скорость и переносное ускорение обозначают и .

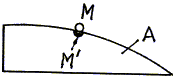
Рис. 66

Движение точки М (рис. 65) относительно стойки (или относительно Охуz) называется абсолютным движением точки М. Скорость и ускорение точки в этом движении есть абсолютная скорость и абсолютное ускорение точки М, их обозначают и .

Обратите внимание на взаимную связь относительного и переносного движений: относительное движение – движение точки по перемещающемуся телу, движение же этого тела – переносное движение. Обратите также внимание на различие в определениях относительного и абсолютного движений, хотя эти определения формально очень похожи.

Важной операцией исследования кинематики сложного движения является выделение относительного, переносного и абсолютного движений в конкретном случае сложного движения точки. Эту операцию будем называть анализом сложного движения точки. Анализ выполняется в соответствии с установленными выше определениями относительного, переносного и абсолютного движений. Для рассмотренного выше случая (см. рис. 65) результат анализа будет таким:

- относительное движение – движение точки М по телу А;

- переносное движение – движение тела А относительно тела В (относительно стойки);

- абсолютное движение – движение точки М относительно тела В (относительно стойки).

При анализе сложного движения точки надо иметь в виду, что объектом относительного и абсолютного движений является одна и та же точка; объектом же переносного движения является тело, по которому точка совершает относительное движение. Из-за наличия взаимной связи относительного и переносного движений их выделение происходит всегда одновременно: если Вы указали относительное движение точки по перемещающемуся телу, то перемещение этого тела следует назвать переносным движением.

Рассмотрим выполнение анализа сложного движения точки на конкретных примерах.

Пример 37. Мостовой кран АВ (рис. 67) перемещается вдоль цеха, изображенного на рисунке прямоугольником ОСDE. По крану движется тележка М. Требуется выполнить анализ сложного движения тележки.

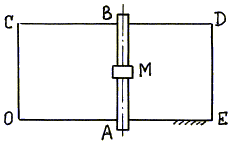
Рис. 67

Начнем с выделения относительного движения, учитывая, что это движение точки по перемещающемуся телу. В данном примере относительное движение – движение тележки М (точки М) по крану.

После того как относительное движение названо, становится очевидным, что переносное движение – движение крана АВ вдоль цеха OCDE.

В завершение укажем абсолютное движение. По определению – это движение точки относительно стойки (неподвижной системы отсчета). В рассматриваемом примере абсолютное движение – движение тележки относительно цеха OCDE.

Пример 38. По трубке, изогнутой в форме окружности, непрерывно течет жидкость. Трубка, в свою очередь, вращается вокруг оси О, перпендикулярной стойке (рис. 68). Требуется выполнить анализ сложного движения частицы М жидкости.

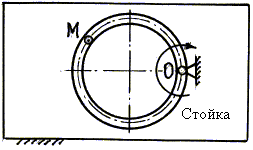
Рис.68

Относительным движением или движением точки по перемещающемуся телу здесь будет движение частицы М по трубке. Переносное движение – вращение трубки вокруг оси О стойки. Абсолютное движение – движение частицы М относительно стойки.

Возвращаясь к условию двух приведенных примеров, отметим, что относительное и переносное движения в них были, по существу, заданы: была известна траектория относительного движения (прямая – в первом примере, окружность – во втором). Так же был определен и вид переносного движения (в первом примере – поступательное движение крана, во втором – вращение трубки вокруг оси). Траектория же абсолютного движения точки в этих примерах не определялась, так как предполагалось, что все параметры абсолютного движения могут быть найдены по заданным параметрам относительного и переносного движений.

Значительная часть задач на сложное движение точки имеет иной характер: условием задачи определяется траектория абсолютного движения точки, а параметры относительного или переносного движения требуется найти. Такие задачи можно считать обратными по отношению к задачам, рассмотренным в первых примерах.

Приведем примеры обратных задач.

Пример 39. На неподвижную проволочную окружность надето колечко М (рис. 69), через него проходит стержень ОА, вращающийся вокруг оси О, перпендикулярной стойке. Требуется выполнить анализ сложного движения колечка М.

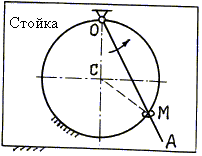
Рис. 69

Абсолютное движение или движение точки относительно неподвижного тела в этом примере отчетливо видно: это движение колечка М по проволочной окружности, расположенной на стойке. Относительное движение или движение точки по перемещающемуся телу здесь – скольжение колечка М по стержню ОА, а переносное движение – вращение стержня ОА вокруг оси О стойки.

Пример 40. Кулачок А (рис. 70), перемещаясь по горизонтальной плоскости вдоль оси х, приводит в движение толкатель ВМ, скользящий в вертикальных направляющих. Требуется выполнить анализ сложного движения точки М толкателя. Точка М толкателя движется относительно неподвижной плоскости (стойки) по вертикали. Это, очевидно, абсолютное движение точки М.

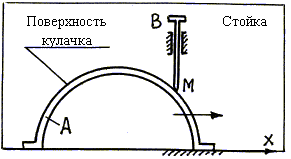
Рис. 70

Можно заметить также, что точка М толкателя скользит по поверхности движущегося кулачка. Это знакомое нам сочетание относительного и переносного движений: относительное – движение точки М по поверхности кулачка, переносное – движение кулачка.

Выполнить разделение движений в подобных задачах будет значительно проще, если в месте контакта звеньев поместить дополнительное тело пренебрежимо малых размеров. Это точечное тело должно проскальзывать по одному звену и в то же время совпадать с точкой контакта второго звена. Таким дополнительным телом может быть колечко, ползун, шарик. Дополнительное тело можно считать точкой, совершающей сложное движение.

В условиях примера 40 поместим в точке контакта кулачка и толкателя шарик М (рис. 71).

При движении кулачка вдоль оси х (переносное движение) шарик М будет перекатываться по поверхности кулачка (относительное движение шарика) и подниматься вверх вместе с толкателем (абсолютное движение шарика).

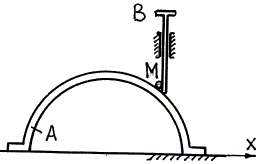
Рис.71

Как видим, после установки шарика легче выявить относительное и переносное движения.

Введение дополнительных тел особенно целесообразно в случаях, когда передача движения от звена к звену осуществляется с помощью гибких поворачивающихся нитей.

Пример 41. В механизме на рис. 72 движение штока АМ в горизонтальных направляющих передается посредством гибкого троса грузу В. Чтобы установить зависимость между характеристиками движения штока АМ и груза В, надо представить, что точка М совершает сложное движение.

Ее движение относительно стойки по горизонтали, очевидно, – абсолютное движение.

Увидеть относительное и переносное движения поможет введение стержня ОС (рис. 73), поворачивающегося вокруг О, и ползуна М, скользящего на этом стержне. (Шток АМ и ползун М соединены шарнирно).

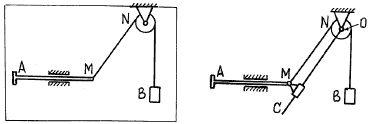
Рис. 72                         Рис. 73

При таком дополнении механизма горизонтальное движение штока АМ вызывает не только подъем (или опускание) груза В, но и поворот стержня ОС вокруг О, а также скольжение ползуна М по стержню. Очевидно, относительным движением точки М (ползуна М) надо считать ее движение вдоль стержня ОС, а переносным движением – поворачивание стержня ОС вокруг О.

Если теперь вернуться к схеме механизма на рис. 72, то можно считать, что относительное движение точки М есть ее движение вдоль троса МN, а переносное движение – поворачивание троса вокруг N. Увидеть это без рассмотрения схемы на рис. 73 затруднительно.

4.2. Определение скоростей в сложном движении точки

Напомним установленные в подразд. 4.1 определения и обозначения:

- относительной скоростью точки называется ее скорость в движении относительно перемещающегося тела, обозначение – ;

- переносной скоростью называется скорость точки перемещающегося тела, с которой в данный момент совпадает движущаяся по телу точка (см. рис. 66), обозначение – ;

- абсолютной скоростью точки называется ее скорость в движении относительно неподвижного тела, обозначение – .

Зависимость между скоростями определяется теоремой: абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей, т.е.

.                                                             (93)

Из уравнения (93) следует, что абсолютная скорость есть диагональ параллелограмма, построенного на переносной и относительной скоростях. Если параллелограмм Меаr (рис. 74) построить в масштабе, то тем самым задача по определениюбудет решена: модуль абсолютной скорости равен длине диагонали Ма в принятом масштабе, а направление абсолютной скорости – от М к а.

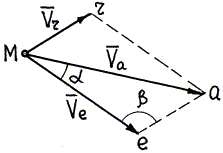
Рис. 74

Но при решении задач кинематики параллелограмм скоростей Меаr обычно рассматривается как вспомогательный чертеж, а модуль и направление искомой скорости определяется аналитически с использованием известных из геометрии соотношений между элементами треугольника (имеется в виду теорема косинусов и т.д.), иначе говоря, задача сводится к решению треугольника Mear. При этом искомой величиной может быть не только , а любой из пяти элементов треугольника – , , , , .

Задача будет разрешимой, если из пяти указанных элементов неизвестными будут два, например, и , и . Это значит, перед тем, как решать треугольник, надо по условию задачи определить, по крайней мере, три элемента треугольника. Эти три элемента или три кинематические характеристики будем в дальнейшем называть предварительно определяемыми.

Во многих случаях предварительно определяемые величины легко отождествляются с величинами, заданными условием задачи. В остальных случаях их можно найти по данным задачи с использованием формул “Кинематики точки” или “Кинематики твердого тела” (см. разд. 1, 2, 3).

При решении задач определенную сложность для начинающих представляет правильное построение параллелограмма скоростей по уравнению (93). Рекомендуется делать это в следующем порядке.

Вначале на расчетной схеме надо провести три линии, по которым должны быть направлены , , . Эти линии будем обозначать соответственно а–а, е–е, r–r (рис. 75); они должны проходить через точку М, которая по условию задачи совершает сложное движение.

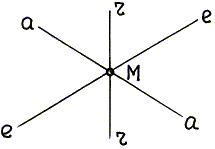
Рис. 75

Линия а–а проводится по касательной к траектории абсолютного движения; линия r–r – по касательной к траектории относительного движения; линия e–e – проводится в соответствии с правилами, установленными для соответствующего движения тела.

Если положение какой-либо линии скорости установить по условию задачи нельзя, то ее следует провести под некоторым углом к уже проведенной линии скорости, считая в дальнейшем α искомой величиной.

Далее на расчетной схеме надо изобразить в произвольном масштабе скорость, направление которой задано условием задачи; ее надо отложить от точки М по соответствующей линии; построить параллелограмм скоростей, следя за тем, чтобы была диагональю этого параллелограмма (рис. 76).

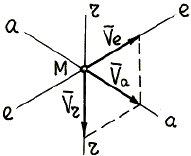
Рис.76

Как обобщение вышесказанного, предлагается такая последовательность операций при решении задачи скоростей в сложном движении точки.

По условию задачи нарисовать расчетную схему, на которой отметить точку М, совершающую сложное движение.

Указать относительное, переносное и абсолютное движение в соответствии с рекомендациями подразд. 4.1.

Провести через точку М линии скоростей а–а, е–е, r–r в соответствии с пояснениями к рис. 75.

Отложить от точки М заданную скорость по соответствующей линии, а затем построить параллелограмм скоростей (рис. 76).

Найти по условию задачи три предварительно определяемые величины.

Решая треугольник Меа (рис. 74 или 76), найти оставшиеся искомые величины.

Пример 42. Вдоль цеха по рельсам с постоянной скоростью 0,1 м/с перемещается мостовой кран АВ, по которому с постоянной скоростью 0,2 м/с движется тележка М. Определить абсолютную скорость тележки.

Решение:

1. На расчетной схеме (рис. 77) изображена точка М (тележка), совершающая сложное движение и подвижное тело – кран АВ в заданный момент времени.

2. Результаты анализа сложного движения тележки (пример 37):

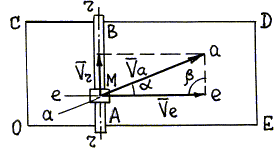
Рис. 77

- относительное движение – движение тележки М по крану АВ;

- переносное движение – движение крана АВ относительно цеха ОСDE;

- абсолютное движение – движение тележки М относительно цеха.

3. Проводим через точку М линии скоростей. Траектория относительного движения точки М – прямая АВ, поэтому линия r–r совпадает с АВ; переносным движением является поступательное движение крана вдоль стороны ОЕ цеха, поэтому линия e–e проведена параллельно OE; траекторию абсолютного движения точки М установить по условию задачи нельзя, поэтому линию а–а проводим под некоторым углом к линии е–е, считая искомой величиной.

4. Построим параллелограмм скоростей: по условию задачи известны направления относительной скорости точки (она равна скорости движения тележки по крану) и переносной скорости (она равна скорости точки крана, с которой в данный момент совпадает тележка); откладываем от точки М по линии r–r вектор относительной скорости , а по линии е–е – вектор переносной скорости ; затем достраиваем параллелограмм скоростей.

5. По условию задачи имеем = 0,2 м/с, = 0,1 м/с, угол = 90⁰ .

6. Решая треугольник Меа (рис. 77), находим

м/с;

.

Пример 43. По трубке, изогнутой в форме окружности радиуса R = 20 см (рис. 78), течет жидкость с постоянной относительно трубки скоростью 40 см/с. Трубка вращается вокруг оси О с постоянной угловой скоростью = 1 1/с. Найти абсолютную скорость частицы жидкости, когда она занимает в трубке положение, определяемое углом ОСМ, равным 120⁰ . Направления вращения трубки и течения жидкости (по трубке) – против хода стрелки часов.

Решение:

1. Расчетная схема с указанием частицы М жидкости в заданном положении изображена на рис. 78.

2. Результаты анализа сложного движения частицы М (пример 38):

- относительное движение – движение частицы М по трубке;

- переносное движение – вращение трубки вокруг оси О стойки;

- абсолютное движение – движение частицы М относительно стойки.

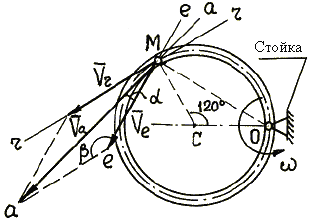
Рис. 78

3. Проводим через точку М линии скоростей: траектория относительного движения точки М – окружность с центром в точке С, поэтому линия r–r проведена по касательной к этой окружности; переносным движением здесь является вращение трубки вокруг оси О, поэтому линия е–е проведена перпендикулярно ОМ, т.е. по направлению скорости точки М' трубки; траекторию абсолютного движения точки М здесь, как и в задаче 42, заранее установить нельзя, поэтому линию а–а проводим под углом к линии е–е, считая искомой величиной.

4. Построение параллелограмма скоростей: по условию задачи известны направления (– скорость движения по трубке) и (– скорость точки М' трубки), откладываем от точки М векторы и по линиям r–r и e–e; затем достраиваем параллелограмм скоростей.

5. Предварительные вычисления: по условию задачи имеем = 40 см/с, модуль переносной скорости определяем по формуле

см/с,

из схемы на рис. 78 следует, что = 150⁰ .

6. Решая треугольник Mea, находим

см/с;

Пример 44. На неподвижную проволочную окружность радиуса 20 см надето колечко М (рис. 79); через него проходит стержень ОА, который вращается вокруг оси О против часовой стрелки с угловой скоростью = 1 1/с. Найти относительную, переносную и абсолютную скорости колечка М в момент, когда угол ОСМ равен 90° .

Решение:

1. Расчетная схема с указанием колечка М в заданном положении (угол ОСМ равен 90⁰ ) изображена на рис. 79.

2. Результаты анализа сложного движения колечка М (пример 39):

- относительное движение – движение колечка М по стержню ОА;

- переносное движение – вращение стержня ОА вокруг оси О стойки;

- абсолютное движение – движение колечка М относительно стойки по окружности радиуса СМ.

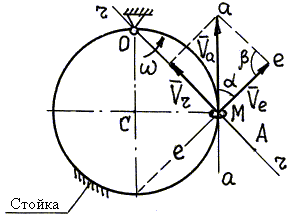
Рис. 79

3. Проводим через точку М линии скоростей: линия r–r проведена вдоль ОА – траектории относительного движения; линия е–е проведена перпендикулярно ОА, – так направлена скорость точки М' стержня ОА (переносная скорость ); траектория абсолютного движения колечка М – окружность с центром в точке С, поэтому линия а–а проведена по касательной к этой окружности.

4. Построение параллелограмма скоростей: по условию задачи известно направление (– скорость точки М' стержня ОА), откладываем ее от точки М по линии е–е; далее достраиваем параллелограмм скоростей, чтобы была диагональю.

5. Предварительные вычисления: по условию задачи определяем

см/с;

из схемы на рис.79 следует, что = 45⁰, = 90⁰ .

6. Решая треугольник Меа, находим см/с,

см/с.

Пример 45. В кулисном механизме (рис. 80) при вращении кривошипа ОМ вокруг оси О ползун М, перемещаясь вдоль стержня АВ, приводит этот стержень во вращательное движение вокруг оси А. Для положения механизма, изображенного на рисунке, определить скорость перемещения ползуна М по стержню АВ и угловую скорость стержня АВ, если угловая скорость кривошипа ОМ = 2 1/с, длина кривошипа ОМ равна 10 см. Кривошип вращается против часовой стрелки.

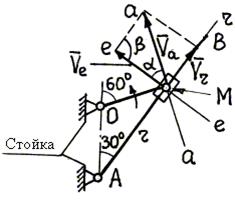
Рис.80

Решение:

1. Расчетная схема механизма изображена на рис.80.

2. Результаты анализа сложного движения ползуна М (пример 40):

- относительное движение – движение ползуна М по стержню АВ;

- переносное движение – вращение стержня АВ вокруг оси А стойки;

- абсолютное движение – движение ползуна М относительно стойки по окружности радиуса ОМ.

3. Проводим через точку М линии скоростей: линия r–r проведена вдоль АВ, т.е. по траектории относительного движения ползуна М; линия е–е проведена перпендикулярно АВ – так направлена скорость точки М' стержня АВ (или переносная скорость); линия а–а проведена перпендикулярно ОМ, что соответствует направлению касательной к окружности радиуса ОМ – траектории абсолютного движения ползуна М.

4. Построение параллелограмма скоростей: по условию задачи известно направление , откладываем ее от точки М по линии а–а. Далее достраиваем параллелограмм скоростей, в котором – диагональ.

5. Предварительные вычисления: по условию задачи определяем

см/с;

из схемы на рис.80 следует = 30⁰, = 90⁰ .

6. Решая треугольник Меа, находим

см/с;

см/с.

После этого определяем угловую скорость стержня АВ

1/с.

Пример 46. Кулачок А (рис. 81), перемещаясь по горизонтальной плоскости вдоль оси х, приводит в движение толкатель ВМ, скользящий в вертикальных направляющих. Определить скорость толкателя в вертикальных направляющих в положении механизма, изображенного на рис. 81, если в этот момент скорость кулачка равна 30 см/с.

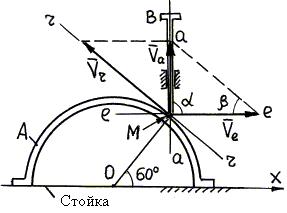
Рис.81

Решение:

1. Расчетная схема изображена на рис. 81.

2. Результаты анализа сложного движения точки М (см. пример 41):

- относительное движение – движение точки М по поверхности кулачка А;

- переносное движение – движение кулачка А относительно стойки;

- абсолютное движение – движение точки М относительно стойки по вертикали.

3. Проводим через точку М линии скоростей: линия r–r проведена по касательной к поверхности кулачка или иначе – по касательной к траектории относительного движения; линия e–e проведена параллельно оси х – так направлена скорость точки кулачка, с которой в данный момент совпадает конец М толкателя ВМ (или переносная скорость ); линия а–а проведена по вертикали – по траектории абсолютного движения.

4. Построение параллелограмма скоростей: по условию задачи известно направление , откладываем ее от точки М по линии е–е; далее достраиваем параллелограмм скоростей, в котором – диагональ.

5. По условию задачи имеем = 30 см/с. Из схемы на рис. 81 следует, что = 90⁰, = 30⁰ .

6. Решая треугольник Меа, находим искомую скорость толкателя

см/с.

Пример 47. В механизме на рис. 82 определить зависимость между скоростью штока АМ и скоростью опускания груза В (угол задан).

Решение:

1. Расчетная схема изображена на рис. 82.

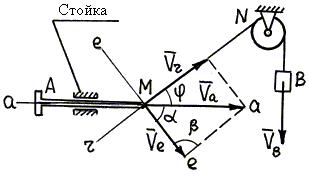
Рис.82

2. Результаты анализа сложного движения точки М (см. пример 42):

- относительное движение – движение точки М вдоль троса МN;

- переносное движение – вращение троса MN вокруг точки N;

- абсолютное движение – движение точки М относительно стойки по горизонтали.

3. Проводим через точку М линии скоростей; линии а–а и r–r совпадают с прямолинейными траекториями абсолютного и относительного движений; линия е–е проведена перпендикулярно MN – так направлена скорость точки M' троса в переносном вращательном движении вокруг N.

4. Построение параллелограмма скоростей: по условию задачи известно направление скорости (вниз), для точки М это соответствует заданию ; откладываем по линии r–r, а затем достраиваем параллелограмм скоростей, в котором – диагональ.

5. Из схемы на рис. 82 следует, что , = 90⁰ .

6. Решая треугольник Меа, находим

Учитывая, что V_r = V_B, V_a = V_АМ, получим

.

4.3. Определение ускорений в сложном движении точки

Зависимость между ускорениями определяется теоремой Кориолиса: абсолютное ускорение точки равно геометрической сумме переносного , относительного и кориолисова ускорений, т.е.

.                                                            (94)

Прежде чем приступить к решению этого уравнения в конкретной задаче, надо установить по каким формулам определяются , , , .

Абсолютное ускорение . Напомним определение (см. подразд. 4.1): абсолютным ускорением точки называется ее ускорение в движении относительно неподвижного тела. Вид формулы зависит от формы траектории абсолютного движения точки.

Если траектория – прямая линия, то

                                                                  (95)

Ускорение в этом случае совпадает с траекторией точки. Направление вектора по траектории точки определяется знаком производной (95): при знаке “плюс” направлено в сторону положительного отсчета расстояний на траектории, при знаке “минус” – в противоположную сторону.

Если траектория абсолютного движения – окружность, то

,                                                              (96)

где – касательное абсолютное ускорение; – нормальное абсолютное ускорение; R – радиус окружности.

Направление вектора по касательной устанавливается с учетом знака производной [см. пояснения к формуле (96)]. Вектор всегда направляется по радиусу окружности к ее центру.

Если траектория абсолютного движения не задается, то абсолютное ускорение следует разложить на составляющие по направлениям осей прямоугольной системы координат Охуz:

для плоских кривых

;                                                                        (97)

для пространственных кривых

.                                                               (98)

Переносное ускорение . Напомним определение (см. подразд. 4.1): переносным ускорением называется ускорение точки перемещающегося тела, с которой совпадает в данный момент движущаяся по этому телу точка.

Вид формулы определяется характером переносного движения.

Если переносное движение тела – поступательное, то в качестве можно взять ускорение любой точки этого тела. (Напомним, что все точки тела при поступательном движении имеют одинаковые ускорения).

Если переносное движение тела – вращение вокруг неподвижной оси, то

,                                                                 (99)

где – вращательное переносное ускорение; – осестремительное переносное ускорение.

В этих формулах и – угловая скорость и угловое ускорение тела; h – расстояние от точки М до оси вращения или радиус вращения точки.

Вектор направлен перпендикулярно радиусу вращения в сторону дуговой стрелки углового ускорения . Вектор направлен по радиусу к оси вращения.

Если переносным движением будет плоскопараллельное или какое-либо более сложное движение тела, то формулы для определения следует взять из соответствующего раздела кинематики твердого тела.

Относительное ускорение . Напомним определение (см. подразд. 4.1): относительным ускорением точки называется ее ускорение в движении относительно перемещающегося тела.

Вид формулы определяется характером траектории относительного движения.

Если траектория – прямая линия, то

                                                         (100)

Ускорение в этом случае совпадает с траекторией точки. Направление вектора по траектории определяется знаком производной (100): при знаке “плюс” направлено в сторону положительного отсчета расстояний на траектории, при знаке “минус” – в противоположную сторону.

Если траектория относительного движения – окружность, то

,                                                       (101)

где– касательное относительное ускорение; – нормальное относительное ускорение; R – радиус окружности.

Направление вектора по касательной устанавливается с учетом знака [см. пояснения к формуле (100)]. Вектор направляется по радиусу окружности к ее центру.

Если траектория относительного движения не задается, то относительное ускорение следует разложить на составляющие по направлению осей прямоугольной системы координат Oxyz:

для плоских кривых

;                                                          (102)

для пространственных кривых

.                                               (103)

Ускорение Кориолиса выражается формулой

.                                                          (104)

Чтобы определить модуль и направление , нужно выполнить следующие операции:

– отложить от точки M (рис. 83) вектор переносной угловой скорости и вектор относительной скорости точки . (Напомним, что вектор направляется по оси вращения в сторону, определяемую правилом правого винта);

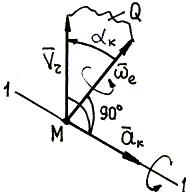
Рис.83

– определить по правилу векторного произведения (104) направление ускорения : для этого надо провести через векторы и плоскость Q; затем провести прямую 1-1, перпендикулярную плоскости Q; наконец, направить по прямой 1–1 вектор в ту сторону, откуда вращение вектора к видно происходящим против хода часовой стрелки (см. рис. 83);

– определить модуль ускорения как модуль векторного произведения (104):

,                                                      (105)

где – угол между векторами и .

Если переносное движение поступательное, то = 0, следовательно, равно нулю. Ускорение Кориолиса равно нулю также, если векторы и параллельны, или когда один из этих векторов обращается в нуль в рассматриваемый момент времени.

После того, как вид формул определения , , , и установлен, рекомендуется переписать уравнение (94) с учетом того, что некоторые члены уравнения будут представлены составляющими.

Допустим, по условию задачи траектория абсолютного движения – окружность, переносное движение – вращение тела вокруг оси, а траектория относительного движения – прямая линия; в этом случае уравнение (94) с учетом (96), (99), (100) примет вид

.                                              (106)

В других задачах число слагаемых в левой и правой частях уравнения (106), конечно, может быть иным.

Для решения уравнения типа (106) оно проектируется на оси подвижной или неподвижной системы координат. Если все векторы этого уравнения лежат в одной плоскости, то будем иметь два уравнения проекций, для пространственной задачи – три уравнения проекций.

Отсюда следует, что в плоских задачах уравнение (106) будет разрешимо, если в нем содержится не более двух, а в пространственных – не более трех неизвестных величин.

В качестве неизвестных могут быть любые величины, входящие в выражения абсолютного, переносного, относительного и Кориолисова ускорений или же сами эти ускорения.

Значит, решению уравнения типа (106) должно предшествовать предварительное определение части величин, входящих в выражения , , и . Они определяются из условия задачи по известным соотношениям кинематики точки и тела; во многих случаях используются результаты определения скоростей в данной задаче.

Как обобщение всего вышесказанного, предлагается такая последовательность операций при решении задачи в сложном движении точки.

1. Нарисовать по условию задачи расчетную схему, на которой отметить точку М, совершающую сложное движение.

2. Указать относительное, переносное и абсолютное движение точки в соответствии с рекомендациями подразд. 4.1.

3. Записать векторное уравнение (94) и провести его анализ: установить формулы для определения , , и [см. формулы (95)... (105)]; преобразовать уравнение (94) в уравнение типа (106); выполнить предварительные вычисления так, чтобы в уравнении типа (106) осталось не более двух неизвестных величин в плоских задачах, и не более трех – в пространственных задачах; отложить все указанные ускорения или их составляющие от точки М на расчетной схеме.

4. Спроектировать уравнение типа (106) на оси выбранной системы координат. Из получившихся алгебраических уравнений проекций определить оставшиеся неизвестные величины.

Пример 48. Со стержня ОА (рис. 84), вращающегося с постоянной угловой скоростью вокруг вертикальной оси z, слетает колечко M. В условиях пренебрежимо малого трения движение колечка по стержню описывается законом

                              (107)

где – расстояние от оси вращения до колечка в начальный момент. Положительное направление отсчета расстояний показано на рис. 84 стрелкой ; e – основание натурального логарифма.

Определить абсолютное ускорение колечка.

Решение:

1. Расчетная схема с указанием колечка М, совершающего сложное движение, изображена на рис. 4.21.

2. Анализ движения: движение колечка М по отношению к стойке (абсолютное движение) складывается из движения колечка вдоль стержня ОА и движения вместе со стержнем.

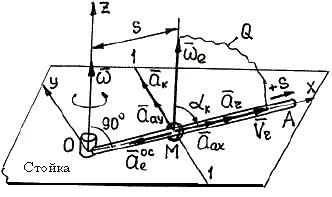
Рис.84

Первое из складываемых движений является относительным, второе – переносным.

3. Запишем векторное уравнение (94):

                                           (108)

Установим формулы для определения ускорений, входящих в уравнение (108), и выполним предварительные вычисления.

Абсолютное ускорение . Напомним, что вид формулы зависит от формы траектории абсолютного движения точки. Эта траектория в рассматриваемом примере – плоская кривая, форма которой не задается. Поэтому вектор представляем в соответствии с (97) составляющими по направлению осей х и у (см. рис. 84)

.

Переносное ускорение . Напомним, что вид формулы определяется характером переносного движения. В данной задаче переносным движением является вращение стержня ОА вокруг оси z. Поэтому вектор представим в соответствии с (99) в виде

,

где ; ;

S – расстояние от точки M до оси вращения z [см. формулу (107)];

– переносная угловая скорость, равная заданной угловой скорости стержня ОА, ; вектор направлен по оси вращения z в сторону, определяемую правилом правого винта (рис. 84); – переносное угловое ускорение, равное в данном случае нулю, так как по условию задачи = const.

В результате ,

Вектор направлен по радиусу к оси вращения z. Так как , то окончательно будем иметь

Относительное ускорение . Напомним, что вид формулы определяется характером траектории относительного движения. В данной задаче эта траектория – прямая линия ОА. Поэтому по формуле (100) имеем:

Производная получилась со знаком “плюс”, поэтому вектор направляется по прямой ОА в сторону положительного отсчета координаты S, т.е. от M к А. Отметим, что для любого момента времени.

Ускорение Кориолиса . Модуль и направление вектора выражается формулой (104):

.

Вектор направлен по оси z, его модуль задан условием задачи. Относительная скорость определяется по формуле

Производная получилась со знаком “плюс”, поэтому вектор направляется по прямой ОА в сторону положительного отсчета координаты S, т.е. от М к А.

Перенесем векторы и в точку М.

Определим по правилу векторного произведения направление ускорения . Для этого сначала проведем через векторы и плоскость Q (см. рис. 84). Затем проведем прямую 1–1, перпендикулярную плоскости Q. Наконец, направим по прямой 1–1 вектор в ту сторону, откуда вращение вектора к видно происходящим против часовой стрелки (см. рис. 84).

Определим модуль ускорения по формуле (105):

так как здесь угол = 90⁰ .

4. В результате проведенного анализа и предварительных вычислений имеем в уравнении (108) две неизвестные величины: и . Из анализа следует, что все векторы, входящие в уравнение (108), лежат в одной плоскости. Это позволяет перейти к проектированию векторного уравнения на оси координат, но сначала приведем уравнение (108) к виду (106), учитывая предварительные вычисления

.

Спроектируем это уравнение на оси выбранной системы координат:

(на ось х) , так как (см. выше);

(на ось у)

Модуль абсолютного ускорения колечка М равен:

Отметим, что абсолютное ускорение колечка получилось равным кориолисову ускорению. Легко убедиться, что это будет при любом положении колечка на стержне. 

Пример 49. Диск радиуса R (рис. 85) вращается вокруг вертикальной оси OO₁ по закону (положительное направление отсчета угла показано на рис.85 дуговой стрелкой). По дуге большого круга ADB движется точка М по закону ; положительное направление отсчета s от А к D.

Дано: R = 0,5 м, , (- в радианах, s - в метрах, t - в секундах).

Определить: и в момент времени t₁ = 1 с.

Указания. Пример - на сложное движение точки. Для её решения необходимо воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка М на пластине в момент времени t₁= 1 с, и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунках к задаче).

Решение.

Рассмотрим движение точки М как сложное, считая ее движение по дуге ADB относительным (АВ - относительная траектория точки), а вращение диска – переносным движением. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам:

, , (109)

где в свою очередь

, .

Определим все характеристики относительного и переносного движений.

1. Относительное движение. Это движение происходит по закону

. (110)

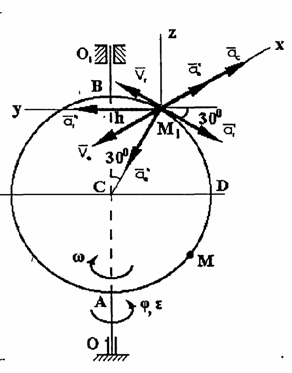
Рис.85

Сначала установим, где будет находиться точка М на дуге ADB в момент времени t₁. Полагая в уравнении (110) t₁ = 1 с, получим

.

Тогда или .

Изображаем на рис. 85 точку в положении, определяемом этим углом (точка M₁). Теперь находим числовые значения , , :

; ; ,

где - радиус кривизны относительной траектории, т.е. дуги ADB. Для момента времени

t₁= 1 с, учитывая, что R = 0,5 м, получим

м/c; м/c2; м/c2. (111)

Знаки показывают, что вектор направлен в сторону положительного отсчета расстояния s, а вектор - в противоположную сторону; вектор направлен к центру С дуги ADB. Изображаем все эти векторы на рис. 4.

2. Переносное движение. Это движение (вращение) происходит по закону . Найдем угловую скорость и угловое ускорение переносного вращения:

,

и при t₁ = 1 с с^-1; с^-2. (112)

Знаки указывают, что при t₁=1с направление совпадает с направлением положительного отсчета угла j, а направление w ему противоположно; отметим это на рис.85 соответствующими дуговыми стрелками.

Для определения и находим сначала расстояние h точки M₁ от оси вращения. Получаем м. Тогда в момент времени t₁ = 1 с, учитывая равенства (4), получим:

м/с, м/с², м/с² . (113)

Изображаем на рис.85 векторы и с учетом направлений и и вектор (направлен к оси вращения).

3.Кориолисово ускорение. Так как угол между вектором и осью вращения (вектором ) равен 60°, то численно в момент времени t₁ = 1 с [см. равенства (111) и (112)]

м/с² . (114)

Направление найдем, спроецировав вектор на плоскость, перпендикулярную оси вращения (проекция направлена так же, как и вектор ), и повернув затем эту проекцию в сторону , т.е. по ходу часовой стрелки, на 90°. Иначе направление можно найти, учтя, что . Изображаем вектор на рис.85.

Теперь можно вычислить значения и .

4. Определение . Так как , а векторы и взаимно перпендикулярны (см. рис.85), то в момент времени t₁ = 1 с

м/с.

5. Определение . По теореме о сложении ускорений

. (115)

Для определения проведем координатные оси (см. рис. 85) и вычислим проекции вектора на эти оси. Учтем при этом, что векторы и лежат на проведенной оси х, а векторы расположены в плоскости дуги ADB, т.е. в плоскости (см. рис. 85). Тогда, проецируя обе части равенства (114) на координатные оси и учтя одновременно равенства (111), (112), (113), получим для момента времени t₁ = 1 с:

м/с²;

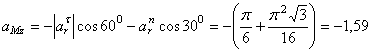м/с²;

м/с².

Отсюда находим значение в момент времени t₁ = 1с:

м/c².

Ответ: = 0,93 м/c; = 4,1 м/c².

Сферическое движение твердого тела

Рассмотрим движение твердого тела, одна из точек которого во все время движения остается неподвижной. При таком движении все остальные точки тела движется по сферическим поверхностям, центры которых совпадают с неподвижной точкой. По этой причине рассматриваемое движение тела называется сферическим движением.

Для определения положения тела в каждый момент времени воспользуемся двумя системами осей координат: неподвижной системой Oxyz с началом в неподвижной точке O и подвижной системой Ox₁y₁z₁, неизменно связанной с твердым телом, с началом в той же точке O (рис.86).

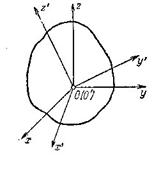
Рис.86

Положение данного тела в пространстве будет вполне определено, если будет известно положение подвижной системы осей Ox₁y₁z₁. Обозначим линию пересечения неподвижной плоскости Oxy и подвижной плоскости Ox₁y₁ через ON и установим на ней положительное направление (от O к N); эта прямая ON называется линией узлов (рис.87). Угол между осью Ox и линией узлов ON обозначим через . Этот угол лежит, очевидно, в плоскости Oxy и отсчитывается от оси Ox в положительном направлении, т.е. против движения часовой стрелки, если смотреть с положительного конца оси . Угол между осями и z₁ обозначим через . Этот угол отсчитывается от оси в направлении, обратном движению часовой стрелки, если смотреть с положительного конца линии узлов ON (). Угол между ON и осью Ox₁ обозначим через . Этот угол лежит в плоскости Ox₁y₁ и отсчитывается от линии узлов против движения часовой стрелки, если смотреть с положительного конца оси .

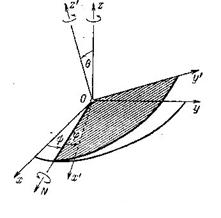
Рис.87

Заданием углов , , однозначно определяется положение подвижной системы осей, связанной с твердым телом, а следовательно, и положение самого тела. Углы , , называются эйлеровыми углами: - угол прецессии, - угол нутации, - угол собственного вращения.

При движении твердого тела, одна из точек которого остается неподвижной, эти углы непрерывно изменяются во времени, т.е.

, , (116)

Уравнения (116), однозначно определяющие сферическое движение тела, называются уравнениями сферического движения твердого тела.

Для определения кинематических характеристик сферического движения тела (угловой скорости, скоростей его точек и т.д.) приведем теорему Эйлера-Даламбера (без доказательства): твердое тело, имеющее одну неподвижную точку, можно переместить из одного положения в любое другое поворотом вокруг некоторой оси, проходящей через неподвижную точку.

Рассмотрим малый промежуток времени , за которое какая-нибудь точка твердого тела перемещается из положения в положение . При этом тело повернулось на угол вокруг некоторой оси (рис.88).

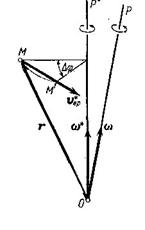
Рис.88

Уменьшая величину промежутка времени , получаем ряд положений оси . Предельное положение этой оси при называется мгновенной осью вращения тела для данного момента времени.

Предел, к которому стремится отношение , когда стремится к нулю, называется угловой скоростью твердого тела в момент

. (117)

Вектор мгновенной угловой скорости в данный момент откладывается по мгновенной оси OP от неподвижной точки O в такую сторону, чтобы, смотря этому вектору навстречу, видеть вращение тела происходящим против движения часовой стрелки. Мгновенная ось вращения представляет собой геометрическое место точек тела, скорости которых в данный момент равны нулю.

Линейная скорость точки M тела в момент времени определяется по формуле

, (118)

где - радиус-вектор точки M, проведенный из неподвижной точки O.

Из (118) следует, что модуль скорости точки M тела равен , где - угол между радиусом-вектором и мгновенной осью вращения . Но , где - расстояние от точки M до оси , т.е. мгновенный радиус вращения точки M. Тогда, окончательно имеем

. (119)

Вектор скорости точки M перпендикулярен к плоскости, проходящей через эту точку и мгновенную ось вращения тела.

Проекции скорости точки на неподвижные оси координат определяются по формулам Эйлера

,

, (120)

.

Здесь: x, y и - координаты точки M; , и - проекции вектора угловой скорости на неподвижные оси координат.

В заключении приводим уравнения мгновенной оси вращения в неподвижной системе осей

. (121)

Рассмотрим несколько примеров.

Пример 50. Твердое тело движется вокруг неподвижной точки O, принятой за начало координат, причем проекции вектора угловой скорости тела на неподвижные координатные оси заданы в виде:

, , .

Найти в момент скорость точки M тела, а также расстояние от нее до мгновенной оси. Координаты точки M в этот момент равны и .

Решение.

Найдем значения проекций угловой скорости при .

, , .

Проекции скорости точки M находим по формулам (8)

,

,

.

Модуль скорости точки M будет равен

.

По заданным проекциям угловой скорости найдем ее модуль

.

Из формулы (119) для расстояния от точки до мгновенной оси вращения получим

.

Пример 51. Конус с углом при вершине 60⁰ и радиусом основания r=20 см катится по неподвижной горизонтальной плоскости без скольжения. Скорость центра основания постоянна и равна . Определить угловую скорость конуса , а также скорости наинизшей и наивысшей точек основания и (рис.89).

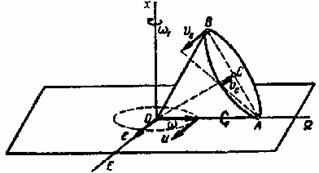
Рис.89

Решение.

Движение катящегося конуса является сферическим, так как его вершина O остается неподвижной. Это движение в каждый момент времени представляет собой вращение вокруг мгновенной оси. Мгновенная ось вращения конуса совпадает с образующей , по которой конус соприкасается с неподвижной плоскостью, так как скорости точек этой образующей равны нулю.

Найдем расстояние от точки C до мгновенной оси

.

Модуль угловой скорости конуса определим по формуле (119)

.

Зная направление скорости , откладываем от точки по мгновенной оси вектор угловой скорости так, чтобы, смотря ему навстречу, видеть вращение конуса вокруг этой оси в сторону, обратную вращению часовой стрелки.

Перейдем к определению скоростей точек и . Скорость точки , лежащей на мгновенной оси вращения, равна нулю, т.е. .

Найдем расстояние от точки до мгновенной оси вращения

.

Воспользовавшись формулой (119), определяем скорость точки .

.

Вектор скорости , так же как и , направлен перпендикулярно плоскости .

Сложение поступательных движений

Пусть твердое тело движется определенным образом относительно системы осей Ox₁y₁z₁, которая в свою очередь совершает одновременно переносное движение по отношению к неподвижным осям Oxyz. Требуется найти результирующее (абсолютное) движение тела, т.е. его движение по отношению к неподвижным осям Oxyz, которое называется сложным движением твердого тела.

Задачей кинематики в этом случае является нахождение зависимостей между характеристиками относительного, переносного и абсолютного движений. Основными кинематическими характеристиками движения тела являются его поступательные и угловые скорости и ускорения. В зависимости от того, какими являются относительное движение тела и движение подвижной системы осей, мы будем иметь задачи о сложении различных движений.

Рассмотрим случай, когда относительное движение тела (движение относительно подвижной системы отсчета) и переносное движение (движение этой подвижной системы отсчета) являются поступательными.

Пусть твердое тело движется поступательно со скоростью относительно некоторой системы отсчета, которая в свою очередь движется поступательно со скоростью относительно другой системы отсчета, принимаемой за неподвижную. Абсолютная скорость какой-нибудь точки тела по теореме сложения скоростей равна геометрической сумме скоростей относительной и переносной, то есть . Но для всех точек тела имеем и , так как относительное и переносное движения являются поступательными. Следовательно . Из последнего равенства видно, что абсолютные скорости всех точек тела в каждый момент одинаковы. Таким образом, приходим к заключению: в том случае, когда относительное и переносное движения являются поступательными, абсолютное движение тела есть также поступательное, причем скорость этого поступательного движения равна геометрической сумме скоростей относительного и переносного движений.

Сложение вращений вокруг двух параллельных осей

Рассмотрим случай, когда относительное движение тела является вращением с угловой скоростью вокруг оси , закрепленной на кривошипе (рис.90,а), а переносное – вращением кривошипа вокруг оси , параллельной , с угловой скоростью . Тогда движение тела будет плоскопараллельным по отношению к плоскости, перпендикулярной к осям.

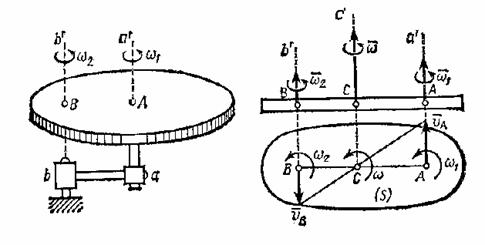
а) б)

Рис.90

Примем, что вращения направлены в одну сторону. Изобразим сечение тела плоскостью, перпендикулярной осям (рис. 90, б). Следы осей в сечении обозначим буквами и . Тогда и . При этом векторы и параллельны друг другу, перпендикулярны и направлены в разные стороны. Тогда точка является мгновенным центром скоростей , а следовательно, ось , параллельная осям и , является мгновенной осью вращения. Для определения угловой скорости абсолютного вращения тела вокруг оси и положения самой оси, т.е. точки , воспользуемся свойством мгновенного центра скоростей

, откуда .

Подставив в эти равенства значения и , окончательно получим

, (122)

. (123)

Итак, при сложении двух направленных в одну сторону вращений вокруг параллельных осей результирующее движение тела будет мгновенным вращением с абсолютной скоростью вокруг мгновенной оси, параллельной данным, положение которой определяется пропорциями (123).

С течением времени мгновенная ось вращения меняет свое положение, описывая цилиндрическую поверхность.

Рассмотрим теперь случай, когда вращения направлены в разные стороны (рис.91).

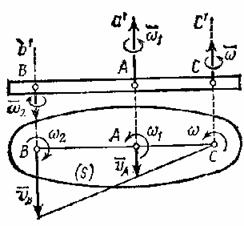
Рис.91

Допустим, что . Тогда, рассуждая, как в предыдущем случае, для угловой скорости абсолютного движения тела вокруг оси и положения самой оси, получим

, (124)

. (125)

Таким образом, при сложении двух направленных в разные стороны вращений вокруг параллельных осей, результирующее движение тела будет мгновенным вращением с абсолютной угловой скоростью вокруг мгновенной оси, положение которой определяется пропорциями (125).

Заметим, что в этом случае точка делит расстояние между параллельными осями внешним образом.

Рассмотрим частный случай, когда вращения вокруг параллельных осей направлены в разные стороны, но по модулю (рис.92).

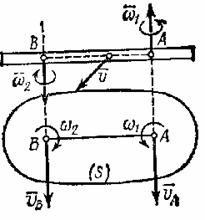
Рис.92

Такая совокупность вращений называется парой вращений, а векторы и образуют пару угловых скоростей. В этом случае получим и , то есть = . Тогда мгновенный центр скоростей находится в бесконечности и все точки тела в данный момент времени имеют одинаковые скорости .

Следовательно, результирующее движение тела будет поступательным (или мгновенно поступательным) движением со скоростью, численно равной и направленной перпендикулярно плоскости, проходящей через векторы и . Таким образом, пара вращений эквивалентна мгновенно поступательному движению со скоростью , равной моменту пары угловых скоростей этих вращений.

Примером пары угловых скоростей является движение велосипедной педали AB относительно рамы велосипеда (рис.93).

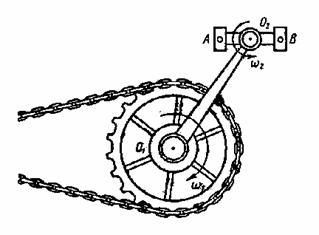
Рис.93

Это движение представляет собой совокупность переносного вращения вместе с кривошипом O₁O₂ вокруг оси O₁ и относительного вращения педали по отношению к кривошипу вокруг оси O₂. Педаль AB за все время движения остается параллельной своему первоначальному положению, т.е. совершает поступательное движение.

Рассмотрим несколько примеров.

Пример 52. Кривошип вращается вокруг оси O₁ по часовой стрелке с угловой скоростью , а диск радиуса вращается вокруг оси O₂ по часовой стрелке с той же угловой скоростью относительно кривошипа. Найти величину и направление абсолютных скоростей точек A и B (рис.94).

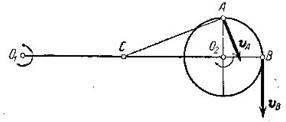
Рис.94

Решение.

Так как угловые скорости переносного и относительного вращений равны по модулю и направлены в одну сторону, то мгновенный центр вращений C диска лежит посредине между O₁ и O₂, т.е. . Модуль абсолютной угловой скорости вращения диска вокруг точки C равен . Отсюда находим:

, ,

, .

Пример 53. Кривошип O₁O₂ вращается вокруг оси O₁ с угловой скоростью . На палец O₂ кривошипа свободно насажена шестерня радиуса r₂, сцепленная с неподвижным зубчатым колесом радиуса r₁. Найти абсолютную угловую скорость шестерни и ее угловую скорость относительно кривошипа (рис.95).

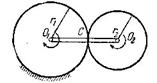
Рис.95

Решение.

Так как шестерня сцеплена с неподвижным колесом, то абсолютная скорость точки С зацепления шестерни с этим колесом равна нулю, т.е. точка С является для шестерни мгновенным центром вращения. Отсюда или ,

Откуда .

Заметим, что направление вращения шестерни совпадает с направлением вращения кривошипа.

Тогда абсолютную угловую скорость шестерни находим из равенства

или

. 

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00