 Моментом силы F
относительно центра (точки) О называется
вектор mo(F) равный векторному произведению
радиуса вектора r, проведенного из центра О в точку
А приложения силы, на вектор силы F:
Моментом силы F
относительно центра (точки) О называется
вектор mo(F) равный векторному произведению
радиуса вектора r, проведенного из центра О в точку
А приложения силы, на вектор силы F: Тема 5. Момент силы относительно центра (точки). Теорема Вариньона
 Моментом силы F
относительно центра (точки) О называется
вектор mo(F) равный векторному произведению
радиуса вектора r, проведенного из центра О в точку
А приложения силы, на вектор силы F:
Моментом силы F
относительно центра (точки) О называется
вектор mo(F) равный векторному произведению
радиуса вектора r, проведенного из центра О в точку
А приложения силы, на вектор силы F:
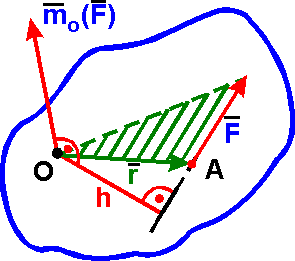
mo(F) = rґF. |
Вектор
mo(F) приложен в точке О и направлен ^ плоскости, проходящей через центр О и силу F, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки.Модуль
mo(F) равен произведению модуля силы F на плечо h:ч mo(F)ч = FЧh, |
где плечо h - перпендикуляр, опущенный из центра О на линию действия силы F.
Момент mo(F) характеризует вращательный эффект силы F относительно центра (точки) О.
1. Момент силы относительно центра не изменяется при переносе силы вдоль линии ее действия в любую точку;
2. Если линия действия силы проходит через центр О (h = 0), то момент силы относительно центра О равен нулю.
Для плоской системы сил при вычислении моментов сил относительно точки (центра), находящейся в той же плоскости, пользуются понятием алгебраического момента силы относительно точки.
Алгебраический момент силы F относительно точки О равен взятому с соответствующим знаком произведению модуля силы на ее плечо:
mo(F) = ± FЧh. |
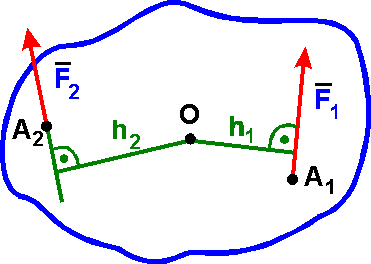 Момент считается положительным, если сила
стремится повернуть тело вокруг точки О против хода часовой стрелки, и отрицательным - по ходу часовой стрелки:
Момент считается положительным, если сила
стремится повернуть тело вокруг точки О против хода часовой стрелки, и отрицательным - по ходу часовой стрелки:
mo(F2) = - F2Чh2. |
При определении алгебраического момента силы относительно точки в случае, когда сложно найти плечо h, следует разложить силу на составляющие, параллельные осям координат, и применить теорему Вариньона: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки О равен сумме моментов составляющих сил, относительно той же точки, т. е.
mo(R) = Smo(Fk), (k = 1, 2, .., n) |
где R = S(Fk) (k = 1, 2, .., n).
Например: F = Fў + FІ, где Fў = FЧcos a, FІ = FЧsin a.
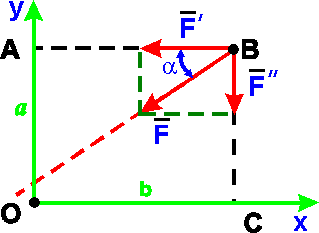
По теореме Вариньона
mo(F) = mo(Fў) + mo(FІ) = FўЧОА - FІЧОС = = FЧcos aЧa - FЧsin aЧb. |