Лекции по динамике

 

Главная

Лекция 1 (продолжение). Задачи для самостоятельного решения

 

1. Динамика прямолинейного движения материальной точки

В задачах 1-30 сила, действующая на точку, является функцией времени.

В задачах 31-60 сила, действующая на точку, является функцией координаты.

В задачах 61-90 сила, действующая на точку, является функцией скорости.

Задача 1. Дрезина массы m = 500 кг движется по горизонтальному прямолинейному участку дороги со скоростью v0 = 90 км/ч. В некоторый момент времени двигатель выключают. Считая, что сила сопротивления движению определяется формулой R = 20t3 (Н), определить время и путь, пройденный дрезиной от момента выключения двигателя до остановки.

Задача 2. На точку веса 50 Н, движущуюся из состояния покоя по горизонтальной прямой Ox, действует в направлении этой оси сила F(t) = 5t2 (Н). Кроме того, на нее действует сила трения. При движении эта сила равна 0,5 Н. Определить момент времени, когда началось движение точки, и найти уравнение ее движения. Считать, что коэффициенты трения покоя и скольжения равны.

Задача 3. Коэффициент трения лыж о снег при движении лыжника по склону горы вниз f = 0.1, угол склона 45°, а его длина 100 м. Определить время спуска и скорость лыжника в конце склона, если в начале она была равна нулю. Сопротивлением воздуха пренебречь.

Задача 4. Автомобиль веса 9,81 кН движется по горизонтальной прямолинейной дороге. В начальный момент его скорость равна 72 км/ч. Затем сила тяги двигателя непрерывно увеличивается пропорционально времени: F = 180t (Н). Найти скорость автомобиля через 10 с и расстояние, которое он пройдет за это время, если на него действует еще и постоянная сила трения с коэффициентом трения f = 0.1.

Задача 5. Хоккеист сообщает шайбе прямолинейное движение. Коэффициент трения шайбы о лед f = 0,05. Чему была равна начальная скорость шайбы, если она прошла до остановки 50 м? За какое время шайба прошла это расстояние? Сопротивлением воздуха пренебречь.

Задача 6. Пуля вылетела из вертикального ствола винтовки со скоростью v0 = 880 м/с и попала в самолет, летевший по горизонтали со скоростью v1 = 720 м/с на высоте h = 400 м. На каком расстоянии от места попадания пули был самолет в момент выстрела? Сопротивлением воздуха пренебречь.

Задача 7. Тяжелая точка поднимается по негладкой наклонной плоскости, составляющей угол α = 30° с горизонтом. В начальный момент скорость точки v0 = 15 м/с. Коэффициент трения f = 0.1. Какой путь пройдет точка до остановки? За какое время она пройдет этот путь?

Задача 8. Материальная точка массы m = 5 кг движется прямолинейно под действием силы , где F0 = 10 (Н) и  (1/с). В начальный момент она имела скорость v0 = 10 м/с. Найти уравнение движения точки и скорость, которую она будет иметь в момент времени t = 2 c.

Задача 9. Вожатый трамвая, выключая постепенно реостат, увеличивает мощность вагонного двигателя так, что сила тяги растет пропорционально времени: F = 1.2t (кН). Найти зависимость пройденного пути от времени движения трамвая, если его масса 10000 кг, а начальная скорость равна нулю. Сила трения постоянна и составляет 0.02 веса трамвая.

Задача 10. На точку веса 49 Н, которая двигалась по горизонтальной прямой, действовала постоянная сила 100 Н. В момент, когда скорость точки равнялась 20 м/с, на нее начала действовать еще сила сопротивления R =10t (Н). Какое расстояние пройдет точка за 6 с после начала действия силы сопротивления? Сколько времени должна действовать эта сила, чтобы скорость точки уменьшилась до нуля?

Задача 11. Автомобиль массы m = 2000 кг движется по горизонтальному прямолинейному участку дороги со скоростью v0 = 80 км/ч. В некоторый момент времени двигатель выключают. Считая, что  сила  сопротивления определяется формулой R = 20t2 (Н), определить время и путь, пройденный автомобилем от момента выключения двигателя до остановки.

Задача 12. На тело веса 100 Н, движущееся из состояния покоя вдоль  горизонтальной оси Ox, действуют вдоль этой же оси сила тяги F = 10t3 (Н) и постоянная сила трения, равная во время движения 0.5 Н. Определить момент времени, когда началось движение тела, и найти уравнение этого движения. Считать, что коэффициенты трения покоя и скольжения равны.

Задача 13. Автомобиль веса 10 кН движется по горизонтальному прямолинейному участку дороги со скоростью v0 = 60 км/ч. В некоторый момент двигатель выключают. Считая, что сопротивление движению определяется формулой R = 20t2 (Н), определить время, за которое скорость автомобиля уменьшилась в 2 раза, и пройденный автомобилем путь от момента выключения двигателя.

Задача 14. Пуля вылетела из вертикального ствола винтовки со скоростью v0 и попала в самолет, летевший по горизонтали со скоростью v1 = 800 м/с на высоте h = 500 м и находившийся в момент выстрела на расстоянии 300 м от места попадания пули в самолет. Какова была начальная скорость пули? Сопротивлением воздуха пренебречь.

Задача 15. Автомобиль массы m = 3000 кг движется со скоростью 60 км/ч по горизонтальной прямолинейной дороге. Затем сила тяги двигателя увеличивается пропорционально времени: F = 200t (Н). Найти момент времени, когда скорость автомобиля увеличится в 2 раза, и расстояние, которое он пройдет за это время, если на него действует сила трения с коэффициентом трения f = 0,2.

Задача 16. Материальная точка массы m = 2 кг прямолинейно движется под действием силы  (Н). В начальный момент точка имела скорость v0 = 20 м/с. Найти уравнение движения точки и скорость, которую она будет иметь в момент времени t = 4 c.

Задача 17. Вожатый трамвая, выключая постепенно реостат, увеличивает мощность вагонного двигателя так, что сила тяги возрастает по закону F = 0,8t2 (кН). Найти момент начала движения и зависимость пройденного пути от времени движения вагона при следующих данных: масса вагона 8000 кг, сопротивление трения  постоянно и составляет 0.05 веса вагона, а начальная скорость равна нулю.

Задача 18. Тяга двигателя ракеты при вертикальном старте возрастает по закону F = 2,5t (кН), масса ракеты 5000 кг. Считая силу тяжести постоянной и пренебрегая сопротивлением воздуха, найти закон движения ракеты на начальном этапе движения.

Задача 19. Точка веса 49 Н двигалась под действием постоянной силы тяги 100 Н по горизонтальной прямой. В момент, когда скорость точки достигла 10 м/с, на нее начала действовать еще одна сила того же направления F =10t (Н). Какое расстояние пройдет точка за первые 10 с после начала действия второй силы? Сколько времени должна действовать эта сила, чтобы скорость точки увеличилась в 5 раз?

Задача 20. Автомобиль массы m = 5000 кг движется по горизонтальному прямолинейному участку дороги со скоростью v0 = 90 км/ч. В некоторый момент времени двигатель выключают. Считая, что сопротивление движению определяется формулой R = 30t2 (Н), найти время, за которое скорость автомобиля уменьшилась в 3 раза, и пройденный автомобилем путь от момента выключения двигателя.

Задача 21. Автомобиль с выключенным двигателем начинает подниматься по негладкой наклонной плоскости, составляющей угол = 30° с горизонтом. В начальный момент скорость автомобиля v0 = 25 м/с. Коэффициент трения f = 0,2. Какой путь пройдет автомобиль до остановки?

Задача 22. Пуля вылетела из вертикального ствола винтовки со скоростью v0 = 800 м/с и попала в самолет, летевший по горизонтали со скоростью v1 = 700 м/с на высоте h = 500 м. На каком расстоянии от места попадания пули был самолет в момент выстрела? Сопротивлением воздуха пренебречь.

Задача 23. Хоккеист сообщает шайбе прямолинейное движение. Чему была равна начальная скорость шайбы, если она прошла до остановки 60 м? За какое время шайба прошла это расстояние, если коэффициент трения шайбы о лед f = 0,1? Сопротивлением воздуха пренебречь.

Задача 24. Вагон массы m = 500 кг двигался по горизонтальному прямолинейному участку дороги с начальной скоростью v0 =20 м/с. Затем на него начала действовать сила сопротивления R = 20t2 (Н). Определить время и путь, пройденный вагоном до остановки.

Задача 25. Автомобиль веса 9,81 кН движется со скоростью 60 км/ч по горизонтальной прямолинейной дороге. Затем сила тяги двигателя непрерывно увеличивается пропорционально времени: F = 200t (Н). Найти скорость автомобиля через 5 с и расстояние, которое он пройдет за это время, если на него действует постоянная сила трения с коэффициентом трения f = 0.2.

Задача 26. Материальная точка массы m = 4 кг  движется прямолинейно под действием силы  (Н). В начальный момент она имела скорость v0 = 20 м/с. Найти уравнение движения точки и ее скорость в момент времени t = 3 c.

Задача 27. Тяга двигателя ракеты при вертикальном старте возрастает согласно закону F = 2,5t2 (кН), масса ракеты 10000 кг. Считая силу тяжести постоянной и пренебрегая сопротивлением воздуха, найти закон движения ракеты.

Задача 28. Тяжелая точка поднимается по негладкой наклонной плоскости, составляющей угол  = 45° с горизонтом. В начальный момент ее скорость v0 = 25 м/с. Коэффициент трения f = 0.1. Какой путь пройдет точка до остановки? За какое время точка пройдет этот путь?

Задача 29. На тело веса 250 Н, движущееся из состояния покоя по горизонтальной прямой, действуют горизонтальная сила F = 25t (Н) и постоянная сила трения, равная во время движения 0.25 Н. Определить момент времени, когда началось движение тела, и найти уравнение этого движения.

Задача 30. Автомобиль веса 20 кН движется по горизонтальному прямолинейному участку дороги со скоростью v0 = 60 км/ч. В некоторый момент времени двигатель выключают. Считая, что сопротивление движению определяется формулой R = 20t2 (Н), определить время, за которое скорость автомобиля уменьшилась в 3 раза, и пройденный автомобилем путь от момента выключения двигателя.

Задача 31. Материальная точка массы m = 10 кг совершает прямолинейное движение под действием силы, изменяющейся по закону F = 1000x (H). В начальный момент точка имела скорость v0 = 10 м/с и координату x0 = 1 м. Найти уравнение движения точки и момент времени, когда скорость точки увеличится в 3 раза, а также путь, который она пройдет за это время.

Задача 32. Материальная точка массы m = 1 кг совершает движение вдоль оси Ох под действием силы F = 100(x - 2) (H). В начальный момент точка имела скорость v0 = 5 м/с и координату x0 = 2,5 м. Найти уравнение движения точки и ее скорость в момент времени t = 3 c.

Задача 33. Материальная точка массы m = 1 кг совершает прямолинейное движение под действием силы сопротивления F = -100e–2x (H). В начальный момент точка имела скорость v0 = 10 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда скорость точки уменьшится в 5 раз, а также путь, который она пройдет за это время.

Задача 34. Материальная точка массы m = 5 кг движется вдоль оси х под действием силы F = 10(x + 2)3 (H). В начальный момент она имела скорость v0 = 4 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда скорость точки увеличится в 2 раза, а также путь, который она пройдет за это время.

Задача 35. Материальная точка массы m = 0.5 кг движется вдоль оси х. В начальный момент точка имела скорость v0 = 10 м/с и координату x0 = 0. Затем на нее начинает действовать сила сопротивления F = -100(x + 1)-3 (H). Найти уравнение движения точки, момент времени, когда скорость точки уменьшится в 2 раза, а также путь, который она пройдет за это время.

Задача 36. Материальная точка массы m = 0.5 кг движется вдоль оси х под действием силы F = 6(x + 0,5)5 (H). В начальный момент она имела скорость v0 = 0.25 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда скорость точки увеличится в 4 раза, а также путь, который она пройдет за это время.

Задача 37. Материальная точка массы m = 2 кг движется вдоль оси х. В начальный момент она имела скорость v0 = 10 м/с и находилась в начале координат. На нее начинает действовать сила F = 400(x + 1)-5 (H). Найти уравнение движения точки, момент времени, когда скорость точки уменьшится в 5 раз, а также путь, который она пройдет за это время.

Задача 38. Материальная точка массы m = 2 кг движется вдоль оси х под действием силы F = 75(x + 1)2 (H). В начальный момент она имела скорость v0 = 5 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда ее скорость увеличится в 4 раза, а также пройденный за это время путь.

Задача 39. Материальная точка массы m = 2 кг движется вдоль оси х при наличии силы сопротивления F = 25(x + 1)-2 (H). В начальный момент она имела скорость v0 = 5 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда ее скорость уменьшится в 10 раз, а также путь, пройденный за это время.

Задача 40. Материальная точка массы m = 200 кг движется вдоль оси х  под действием силы F = 2e2x (H). В начальный момент она имела скорость v0 = 0.1 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда ее скорость увеличится в 2 раза, а также путь, который она при этом пройдет.

Задача 41. Материальная точка массы m = 1 кг движется вдоль оси х  под действием силы F = 400(x + 1) (H). В начальный момент точка имела скорость v0 = 20 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда ее скорость увеличится в 2 раза, а также путь, который она при этом пройдет.

Задача 42. Материальная точка массы m = 2 кг движется вдоль оси х с начальной скоростью v0 = 0 из положения x0 = 1 м. На нее действует сила F = 800(x - 1) (H). Найти уравнение движения точки и ее скорость в момент времени t = 2 c.

Задача 43. Материальная точка массы m = 10 кг с начальной скоростью v0 = 1 м/с движется вдоль оси х из положения x0 = 0. На нее  действует сила сопротивления F = -10e-2x (H). Найти уравнение движения точки, момент времени, когда ее скорость уменьшится в 2 раза, а также путь, который она пройдет за это время.

Задача 44. Материальная точка массы m = 4 кг движется вдоль оси х  под действием силы F = 200(x +1)3 (H). В начальный момент точка имела скорость v0 = 5 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда скорость точки увеличится в 3 раза, а также путь, который она пройдет за это время.

Задача 45. Материальная точка массы m = 1 кг движется вдоль оси х с начальной скоростью v0 = 5 м/с из положения x0 = 0. На нее  действует сила сопротивления F = -100(x + 2)-3 (H). Найти уравнение движения точки, момент времени, когда ее скорость уменьшится в 5 раз, а также путь, который она пройдет за это время.

Задача 46. Материальная точка массы m = 2 кг прямолинейно движется под действием силы F = 0,24(x + 1)5 (H). В начальный момент точка имела скорость v0 = 0.2 м/с и координату x0 = 0. Найти уравнение ее движения, момент времени, когда скорость точки увеличится в 5 раз, а также путь, который она пройдет за это время.

Задача 47. Материальная точка массы m = 1 кг движется вдоль оси x под действием силы F = -50(x + 1)-5 (H). В начальный момент она имела скорость v0 = 5 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда ее скорость уменьшится в 5 раз, а также путь, который она пройдет за это время.

Задача 48. Материальная точка массы m = 0,1 кг движется вдоль оси x под действием силы F = 15(x + 0,5)2 (H). В начальный момент она имела скорость v0 = 10 м/с и координату x0 = 0.5 м. Найти уравнение движения точки, момент времени, когда ее скорость увеличится в 2 раза, а также путь, который она пройдет за это время.

Задача 49. Материальная точка массы m = 1 кг движется вдоль оси x под действием силы F = -18(x + 4)-2 (H). В начальный момент она имела скорость v0 = 3 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда ее скорость уменьшится в 3 раза, а также путь, который она пройдет за это время.

Задача 50. Материальная точка массы m = 25 кг прямолинейно движется вдоль оси x  под действием силы F = e8x (H). В начальный момент она имела скорость v0 = 0.1 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда ее скорость увеличится в 10 раз, а также путь, пройденный за это время.

Задача 51. Материальная точка массы m = 2 кг движется вдоль оси x под действием силы F = 200(x + 2) (H). В начальный момент точка имела скорость v0 = 20 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда ее скорость увеличится в 5 раз, а также пройденный за это время путь.

Задача 52. Материальная точка массы m = 1 кг движется вдоль оси x под действием силы F = 25(x + 2) (H). В начальный момент точка имела скорость v0 = 5 м/с и координату x0 = -3 м. Найти уравнение движения точки и ее скорость в момент времени t = 2 c.

Задача 53. Материальная точка массы m = 2 кг движется вдоль оси х под действием силы F = -32e-8x (H). В начальный момент она имела скорость v0 = 2 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда скорость точки уменьшится в 2 раза, а также путь, который она пройдет за это время.

Задача 54. Материальная точка массы m = 0,5 кг движется вдоль оси х  под действием силы F = 100(x + 0.2)3 (H). В начальный момент она имела скорость v0 = 0.4 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда ее скорость увеличится в 5 раз, а также путь, который она пройдет за это время.

Задача 55. Материальная точка массы m = 10 кг движется вдоль оси х под действием силы F = -250x-3 (H). В начальный момент точка имела скорость v0 = 5 м/с и координату x0 = 1 м. Найти уравнение движения точки, момент времени, когда скорость точки уменьшится в 5 раз, а также путь, который она пройдет за это время.

Задача 56. Материальная точка массы m = 0,25 кг движется вдоль оси х под действием силы F = 0.48(x + 0.5)5 (H). В начальный момент точка имела скорость v0 = 0.1 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда ее скорость увеличится в 5 раз, а также пройденный за это время путь.

Задача 57. Материальная точка массы m = 0,1 кг движется вдоль оси х под действием силы F = -5(x + 0.5)-5 (H). В начальный момент точка имела скорость v0 = 5 м/с и координату x0 = 0.5 м. Найти уравнение движения точки, момент времени, когда ее скорость уменьшится в 5 раз, а также путь, который она пройдет за это время.

Задача 58. Материальная точка массы m = 2 кг движется вдоль оси х под действием силы F = 3(x + 4)2 (H). В начальный момент точка имела скорость v0 = 8 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда ее скорость увеличится в 2,5 раза, а также путь, который она пройдет за это время.

Задача 59. Материальная точка массы m = 0,5 кг движется вдоль оси х под действием силы F = -(x + 3)-2 (H). В начальный момент точка имела скорость v0 = 1 м/с и координату x0 = 1 м. Найти уравнение движения точки, момент времени, когда ее скорость уменьшится в 2 раза, а также путь, который она пройдет за это время.

Задача 60. Материальная точка массы m = 2,5 кг движется вдоль оси х под действием силы, изменяющейся по закону F = 0,1e2x (H). В начальный момент она имела скорость v0 = 0.2 м/с и координату x0 = 0. Найти уравнение движения точки, момент времени, когда скорость точки увеличится в 5 раз, а также путь, который она пройдет за это время.

Задача 61. Свободная материальная точка массы m = 5 кг, имеющая начальную скорость v0 = 40 м/с, движется прямолинейно. На точку действует сила сопротивления, по величине равная F = 50 (v)1/3 (Н). Определить время, прошедшее от начала движения точки до остановки, и путь, пройденный точкой.

Задача 62. Сила тяги винтов вертолета массы m = 5000 кг при вертикальном подъеме в 1.5 раза больше его веса. Сопротивление воздуха R = 300v (Н), где v – скорость подъема вертолета. Считая начальную скорость вертолета v0 = 0, найти закон его движения и предельно достижимую скорость подъема.

Задача 63. Самолет массы m = 15000 кг в момент приземления имел скорость v0 = 50 м/с. Определить, какое расстояние он пройдет и какую будет иметь скорость через 10 с при выключенных моторах, если суммарное сопротивление движению R = 20v2 (Н).

Задача 64. Тело массы m = 2 кг, принимаемое за материальную точку, движется вдоль горизонтальной прямой под действием силы F = 50 (Н). Кроме того, на него действует сила сопротивления R = v, где  = 5 (Нс)/м. Найти закон движения тела, если в начальный момент его скорость равна нулю.

Задача 65. Парусная лодка веса 2000 Н движется со скоростью 1.5 м/с. После снятия паруса лодка движется, преодолевая сопротивление воды R = 50v (Н), где v – скорость лодки, м/с. Определить время, в течение которого скорость лодки уменьшилась в 3 раза, и расстояние, которое она прошла за это время.

Задача 66. В момент, когда гоночный автомобиль веса 8 кН пересекает финиш со скоростью 360 км/ч, водитель выключает двигатель. Учитывая силу сопротивления воздуха , где  = 0.075 (Нс2)/м2, определить время, прошедшее к моменту, когда скорость автомобиля уменьшилась в 2 раза, и расстояние, которое автомобиль прошел за это время.

Задача 67. Сила тяги мотора катера Q = 5 кН, а сопротивление воды определяется формулой R = 10v (Н). Определить закон движения катера и его предельную скорость, если движение начинается из состояния покоя, а масса катера 2000 кг.

Задача 68. Лодка с человеком, общий вес которых 1,47 кН, двигалась в спокойной воде. Когда человек перестал грести, скорость лодки была равна 2 м/с. Определить расстояние, которое пройдет лодка к моменту, когда ее скорость уменьшится в 4 раза, если сопротивление воды ее движению R = 40v (Н).

Задача 69. Шарик веса 0,05 Н вылетает вертикально вверх из пружинного пистолета со скоростью 10 м/с. Считая, что сопротивление воздуха пропорционально первой степени скорости и равно 0.01 Н при скорости v = 1 м/с, определить максимальную высоту, на которую поднимется шарик, и время достижения этой высоты.

Задача 70. К моменту прекращения работы двигателя аэросани веса 5 кН приобрели скорость v0 = 144 км/ч. Сила сопротивления воздуха R = 2v2 (Н). Какое расстояние пройдут аэросани по горизонтальной поверхности и какую будут иметь скорость через 10 с?

Задача 71. Неподвижное в начальный момент времени тело веса 80 Н падает в среде с сопротивлением R = 20v (Н). Определить максимальное значение скорости падения, а также время, прошедшее к моменту, когда скорость тела достигнет 0.99 ее максимального значения, и расстояние, пройденное телом за это время.

Задача 72. Свободная материальная точка массы m = 4 кг, имеющая начальную скорость v0 = 50 м/с, движется прямолинейно. На точку действует только сила сопротивления R = 60v1/2 (Н). Определить время, прошедшее от начала движения точки до остановки, и путь, пройденный точкой.

Задача 73. Сила тяги винтов вертолета массы m = 4000 кг при вертикальном подъеме в 2 раза больше его веса. Сопротивление воздуха R = 200v (Н), где v – скорость подъема. Найти закон движения вертолета и определить предельно достижимую скорость вертолета.

Задача 74. Самолет массы m = 25000 кг в момент приземления имел скорость v0 = 50 м/с. Определить, какое расстояние он пройдет при выключенных моторах до момента времени, когда его скорость уменьшится в 5 раз, если суммарное сопротивление движению R = 10v2 (Н).

Задача 75. На тело массы m = 4 кг, принимаемое за материальную точку, действуют сила F = 100 (Н) и сила сопротивления , где = 10 (Нс)/м. Найти закон движения тела, а также его максимальную скорость, если в начальный момент его скорость равна 2 м/с. Считать, что точка движется вдоль горизонтальной прямой.

Задача 76. Парусная лодка веса 2500 Н двигалась со скоростью 2 м/с. После снятия паруса она движется, преодолевая сопротивление воды R = 40v (Н), где v – скорость лодки, м/с. Определить время, в течение которого скорость лодки уменьшится в 100 раз, и расстояние, которое она пройдет за это время.

Задача 77. В момент, когда гоночный автомобиль веса 9,81 кН пересекает финиш со скоростью 300 км/ч, водитель выключает двигатель. Учитывая силу сопротивления воздуха , где = 0,05 (Нс2)/м2, определить время, прошедшее к моменту, когда скорость автомобиля уменьшилась в 5 раз, и расстояние, которое автомобиль прошел за это время.

Задача 78. Сила тяги мотора катера Q = 4 кН, а сопротивление воды R = 50v (Н). Определить закон движения катера и предельную скорость, которую он может достичь, если движение начинается из состояния покоя, а масса катера 2500 кг.

Задача 79. Лодка веса 2 кН  двигалась со скоростью 2,5 м/с. Определить расстояние, которое пройдет лодка к моменту, когда скорость лодки уменьшится в 5 раз, если сила сопротивления воды R = 5v2 (Н).

Задача 80. Шарик веса 0,1 Н вылетает вертикально вверх из пружинного пистолета со скоростью 10 м/с. Считая, что сопротивление воздуха R = 0,05v (Н), определить максимальную высоту, на которую поднимется шарик, и время достижения этой высоты. На сколько увеличится максимальная высота подъема, если не учитывать сопротивление воздуха?

Задача 81. К моменту прекращения работы двигателя аэросани веса 4 кН приобрели скорость v0 = 120 км/ч. Сила сопротивления воздуха R = 4v2 (Н). Какое расстояние пройдут аэросани по горизонтальной поверхности до момента времени, когда их скорость уменьшится в 10 раз?

Задача 82. Неподвижное в начальный момент времени тело веса 100 Н падает в некоторой среде по вертикали. Считая, что сопротивление среды R = 40v (Н), определить максимальное значение скорости падения, время, прошедшее к моменту, когда скорость тела достигнет 0,8 ее максимального значения, и расстояние, пройденное телом за это время.

Задача 83. Свободная материальная точка массы m = 5 кг, име­ющая начальную скорость v0 = 100 м/с, движется прямолинейно. На нее действует только сила сопротивления R = 50 v1/2 (Н). Определить время, прошедшее от начала движения точки до остановки, и путь, пройденный точкой.

Задача 84. Сила тяги винтов вертолета массы m = 3000 кг при его вертикальном подъеме в 3 раза больше его веса. Сопротивление воздуха R = 100v (Н), где v – скорость подъема. Считая начальную скорость v0 = 0, найти закон движения вертолета и определить его предельно достижимую скорость подъема.

Задача 85. Движение планера массы m = 250 кг происходит по горизонтальной прямой. Принимая силу сопротивления воздуха в свободном полете планера R = 8v2 (Н), определить расстояние, которое пролетит планер за 10 с от момента времени, когда его скорость была равна 100 м/с.

Задача 86. Свободная материальная точка массы m = 10 кг, имеющая начальную скорость v0 = 100 м/с, движется прямолинейно. На нее действует только сила сопротивления R = 90v1/3 (Н). Определить время, прошедшее от начала движения точки до остановки, и пройденный ею путь.

Задача 87. Самолет массы m = 10000 кг в момент приземления имел скорость v0 = 150 м/с. Определить, какое расстояние он пройдет и какую будет иметь скорость через 10 с при выключенных моторах, если суммарное сопротивление движению R = 10v2 (Н).

Задача 88. На тело массы m = 10 кг, принимаемое за материальную точку, действуют постоянная сила F = 250 (Н) и сила сопротивления R = 10v (Н). Найти закон движения тела, если в начальный момент его скорость была равна нулю. Движение считать проходящим по горизонтальной прямой.

Задача 89. Парусная лодка веса 1000 Н двигалась со скоростью 2,5 м/с. После снятия паруса лодка движется, преодолевая сопротивление воды R = 50v (Н), где v – скорость лодки, м/с. Определить время, в течение которого скорость лодки уменьшилась в 3 раза, и расстояние, которое она прошла за это время.

Задача 90. В момент, когда гоночный автомобиль веса 10 кН пересекает финиш со скоростью 400 км/ч, водитель выключает двигатель. Учитывая силу сопротивления  воздуха , где  = 0,1 (Нс2)/м2, определить время, прошедшее к моменту, когда скорость автомобиля уменьшилась в 4 раза, и расстояние, которое автомобиль прошел за это время.

Задача 91. Автомобиль массой 1 т  останавливается при торможении за 5 с, пройдя при этом равнозамедленно расстояние в 25 м. Найти начальную скорость автомобиля; силу торможения.

Задача 92. Какую силу надо приложить к вагону, стоящему на рельсах, чтобы вагон стал двигаться равноускоренно и за время 30 с прошел путь 11 м? Масса вагона 16 т. Во время движения на вагон действует сила трения, равная 0,05 силы тяжести вагона.

Задача 93. Вагон массой 20 т движется с постоянным отрицательным ускорением, численно равным 0,3 м/с2. Начальная скорость вагона равна 54 км/ч. 1) Какая сила торможения действует на вагон? 2) Через сколько времени вагон остановится? 3) Какое расстояние вагон пройдет до остановки?

Задача 94. Тело массой 0,5 кг движется так, что  зависимость пройденного телом пути s от времени движения t дается уравнением s=Asinωt, где А=5 см и ω=π рад/с. Найти силу, действующую на тело через 1/6 секунду после начала движения.

Задача 95. Трамвай, трогаясь с места, движется с постоянным ускорением 0,5 м/с2. Через 12 с после начала движения мотор трамвая выключается и трамвай движется до остановки равнозамедленно. На всем пути движения трамвая коэффициент трения равен 0,01. Найти: 1) наибольшую скорость движения трамвая, 2) общую продолжительность движения, 3) отрицательное ускорение трамвая при замедленном движении, 4) общее расстояние, пройденное трамваем.

Задача 96. Автомобиль весит 1 т. Во время движения на автомобиль действует сила трения, равная 0,1 его силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью: 1) в гору с уклоном в 1 м на каждые 25 м пути, 2) пол гору с тем же уклоном.

Задача 97. Три груза массой по 1 кг связаны нитью и движутся по горизонтальной плоскости под действием силы 10 Н, направленной под углом 30° к горизонту. Определить ускорение системы и силы натяжения нитей, если коэффициент трения равен 0,1.

Задача 98. Человек везет двое саней массой по 15 кг каждые, связанные между собой веревкой, прикладывая силу 120 Н под углом к горизонту. Найти ускорение саней и силу натяжения веревки, связывающей сани, если коэффициент трения полозьев о снег 0,02.

Задача 99. Масса лифта с пассажирами равна 800 кг. Найти, с каким ускорением и в каком направлении движется лифт, если известно, что натяжение троса, поддерживающего лифт, равно: 1) 12кН; 2) 6 кН.

Задача 100. Поезд массой 500 т после прекращения тяги паровоза под действием силы трения в 98 кН останавливается через 1 мин. С какой скоростью шел поезд?

Задача 101. Под действием постоянной силы 9,8 Н тело движется прямолинейно так, что зависимость пройденного телом расстояния s от времени t дается уравнением s=A-Bt+Ct2. Найти массу тела, если постоянная C=1 м/с2.

Задача 102. Тело лежит на наклонной плоскости, составляющей с горизонтом угол 4°. 1) При каком предельном значении коэффициента трения тело начнет скользить  по наклонной плоскости? 2) С каким ускорением будет скользить тело по плоскости, если коэффициент трения равен 0,03? 3) Сколько времени потребуется для прохождения при этих условиях 100 м пути? 4) Какую скорость тело будет иметь в конце этих 100 м?

Задача 103. Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол 15° с горизонтом. Найти коэффициент трения, если время подъема тела оказалось в x=2 раза меньше времени спуска.

Задача 104. Две гири массой 2 кг и 1 кг соединены нитью и перекинуты через невесомый блок. Найти: 1) ускорение с которым движутся гири; 2) натяжение нити. Трением в блоке пренебречь.

Задача 105. Невесомый блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы α=30° и β=45° (рис.1). Гири А и В равной массы 1 кг соединены нитью и перекинуты через блок. Найти: 1) ускорение, с которым движутся гири, 2) натяжение нити. Трением гирь  А и В о наклонные плоскости, а также трением в блоке пренебречь.

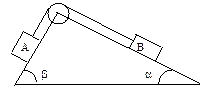
Рис.1

 

Задача 106. Решить предыдущую задачу  при условии, что коэффициенты трения  гирь о наклонные плоскости  равны μ1=μ2=0,1. Трением в блоке пренебречь.

Задача 107. К концам невесомой и нерастяжимой нити, перекинутой через невесомый блок, подвешены два груза массой по 100 г каждый. На один из грузов положен перегрузок массой 10 г. Найти силу, с которой перегрузок давит на груз, а также силу давления на ось блока.

Задача 108. На столе лежит деревянный брусок, к которому привязаны нити, перекинутые через блоки, укрепленные на обоих концах стола. К свободным концам нити подвешены грузы массами 0,85 и 0,2 кг, вследствие чего брусок приходит в движение и за 3 с проходит расстояние 0,81 м. Зная, что масса бруска 2 кг, определить коэффициент трения скольжения и силу натяжения нитей.

Задача 109. Тело скользит по наклонной плоскости, составляющей с горизонтом угол 45°. Зависимость пройденного телом расстояния s от времени t дается уравнением s=Ct2, где С=1,73 м/с2. Найти коэффициент трения тела о плоскость.

Задача 110. На наклонной плоскости длиной 5 м и высотой 3 м находится груз массой 50 кг. Какую силу, направленную вдоль наклонной плоскости, надо приложить, чтобы: 1) удержать этот груз? 2) Втаскивать равномерно вверх? 3) Втаскивать вверх с ускорением 1 м/с2. Коэффициент трения 0,2.

Задача 111. Невесомый блок укреплен на конце стола. Гири А и В равной массы m1=m2=1 кг соединены нитью и перекинуты через блок (рис.2). Коэффициент трения гири В о стол равен 0,1. Найти: 1) ускорение, с которым движутся гири, 2) натяжение нити. Трением в блоке пренебречь.

Рис.2

 

Задача 112. Невесомый блок укреплен на вершине наклонной плоскости, составляющей с горизонтом угол α=30° (рис.3). Гири А и В равной массы 1 кг соединены нитью и перекинуты через блок. Найти: 1) ускорение, с которым движутся гири, 2) натяжение нити. Трением в блоке, а также трением гири В о наклонную плоскость пренебречь.

Рис.3

 

Задача 113. Решить предыдущую задачу при условии, что коэффициент трения гири В о наклонную плоскость равен 0,1. Трением в блоке пренебречь.

Задача 114. Материальная точка массой 2 кг скользит по негладкой горизонтальной плоскости под действием силы F=10 Н, составляющий угол α=30° с горизонтальной плоскостью. Определить ускорение материальной точки, если коэффициент трения скольжения f=0,1.

Задача 115. В шахте опускается равноускоренно лифт массой 280 кг. В первые 10 с он проходит 35 м. Найти натяжение каната, на котором висит лифт.

Задача 116. При выстреле из орудия снаряд вылетает с горизонтальной скоростью 570 м/с. Масса снаряда 6 кг. Определить среднее давление пороховых газов, если снаряд проходит внутри орудия 2 м.

Задача 117. Гвоздь вбивается в стену, оказывающую сопротивление 700 Н. При каждом ударе молотка гвоздь углубляется на l=0,15 см. Найти массу молотка, если при ударе о шляпу он имеет скорость 1,25 м/с.

Задача 118. Для определения массы груженого железнодорожного состава, между тепловозом и вагонами установили динамометр. Среднее показание динамометра за 2  мин. – 106  Н. За то же время состав набрал скорость 16 м/с (в начале стоял на месте). Найти массу состава, если коэффициент трения f=0,02.

Задача 119. Материальная точка поднимается по негладкой наклонной плоскости, составляющей угол α=30° с горизонтом. В начальный момент скорость равнялась 15 м/с. коэффициент трения f=0,1. Найти путь до остановки.

Задача 120. Тело массой 2 кг от толчка поднимается по наклонной плоскости с V0=2 м/с. Определить работу силы тяжести до остановки.

Задача 121. Свободное падение материальной точки массой m начинается из состояния покоя. Пренебрегая сопротивлением воздуха, определить путь, пройденный точкой к моменту времени, когда оно имеет скорость 3 м/с.

Задача 122. Тело массой «m» вследствие толчка прошло по негладкой горизонтальной плоскости за 5 с, расстояние S=24,5 м и остановилось. Найти коэффициент трения.

Задача 123. Материальная точка массой 0,5 кг движется по прямой. Определить модуль импульса равнодействующей за первые 2 с, если она движется по закону s=4t3.

Задача 124. Горизонтальная платформа, на которой лежит груз m=1,02 кг, опускается вертикально вниз с ускорением 4 м/с2. Найти силу давления, производимого грузом на платформу.

Задача 125. На материальную точку массой 1 кг действует сила постоянного направления, F=5cosπt. Определить скорость этой точки в момент времени t=0,5 с, если начальная скорость точки V0=1,5 м/с.

Задача 126. На наклонной плоскости длиной 2,54 м и высотой 0,7 м в верхней точке лежит груз m=50 кг. Какую силу, параллельную наклонной плоскости, нужно приложить к телу, чтобы стащить его вниз по всей длине наклонной плоскости равноускоренно за 5 сек? Коэффициент трения f=0,4.

Задача 127. Тело, которому сообщили начальную скорость V0=5 м/с, скользило по шероховатой горизонтальной плоскости и остановилось через 1 час. Найти коэффициент трения скольжения.

Задача 128. Тело, которому сообщили начальную скорость V0=20 м/с, скользило вверх по шероховатой наклонной плоскости, расположенной под углом 30° к горизонтали, и остановилось. Найти время до остановки, если коэффициент трения скольжения f=0,1.

Задача 129. Молот весом G=20 кН падает с высоты h=1 м на поковочную болванку. Деформация болванки происходит в течении 0,01 с. Определить среднюю величину силы давления молота на болванку.

Задача 130. Определить давление человека массой m = 80 кг на площадку лифта в начале подъема и перед остановкой; ускорение (замедление) лифта а = 0,2g.

Задача 131. Тело спускается по гладкой плоскости, наклоненной под углом 30° к горизонту. Найти, за какое время оно пройдет путь 9,6 м, если в начальный момент его скорость равнялась 2 м/с.

Задача 132. Определить путь пройденной точки массой “m” по оси Ox за время t=1 с, если она движется под действием силы Fx=12mt2. В момент t0=0 x0=3 м Vxo=6 м/с.

Задача 133. Материальная точка m=10 кг движется по горизонтальной прямой под действием силы F=10t, которая направлена по той же прямой. Определить время, за которое скорость точки увеличится с 5 до 25 м/с.

Задача 134. Пуля массой 20 г, вылетает из ствола винтовки со скоростью 650 м/с, пробегая канал ствола за t=0,00095 с. Определить среднюю величину давления газов, выбрасывающих пулю, если площадь сечения канала S=150 мм2.

Задача 135. Железнодорожный поезд движется по горизонтальному и прямолинейному участку пути. При торможении развивается сила сопротивления, равная 0,1 веса поезда. В момент начала торможения скорость поезда равнялась 20 м/с. Найти время торможения и тормозной путь.

Задача 136. Определить модуль равнодействующей силы, действующей на материальную точку m=3 кг в момент t=6 c, если она движется по оси OX по закону x=0,04t3.

Задача 137. Тело m=2 кг движется прямолинейно по закону x=10sin4t под действием силы F. Найти наибольшее значение этой силы.

Задача 138. Груз массы m=100 кг, подвешенный к концу намотанного на барабан троса, движется с ускорением а = 0,3g. Определить натяжение троса при подъеме и опускании груза.

 

2. Динамика криволинейного движения материальной точки

В некоторых задачах используется понятие "плавучесть", означающее разность между подъемной силой Архимеда и силой тяжести. Звездочкой помечены задачи повышенной сложности (варианты 201-210).

Задача 139. Ведерко с водой, привязанное к веревке длиной 60 см, равномерно вращается в вертикальной плоскости. Найти: 1) наименьшую скорость вращения ведерка, при которой в высшей точке вода из него не выливается, 2) натяжение веревки при этой скорости в высшей и низшей точках окружности. Масса ведерка с водой 2 кг.

Задача 140. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу камня, если известно, что разность между максимальным и минимальным натяжениями веревки равна 9,8 Н.

Задача 141. Гирька массой 50 г, привязанная к нити длиною в 25 см, описывает в горизонтальной плоскости окружность. Скорость вращения гирьки соответствует 2 об/с. Найти натяжение нити.

Задача 142. Диск вращается вокруг вертикальной оси, делая 30 об/мин. На расстоянии 20 см от оси вращения на диске лежит тело. Каков должен быть коэффициент трения между телом и диском, чтобы тело не скатилось с диска?

Задача 143. Определить скорость движения автомобиля массой 2 т по вогнутому мосту радиусом 100 м, если он давит на середину моста с силой 25 кН.

Задача 144. Самолет, летящий со скоростью 900 км/ч, делает “мертвую петлю”. Каков должен быть радиус “мертвой петли”, чтобы наибольшая сила, прижимающая летчика к сидению, была равна: пятикратному весу летчика? 2) десятикратному весу летчика?

Задача 145. Средняя высота спутника над поверхностью Земли 1700 км. Определить его скорость и период вращения.

Задача 146. Найти силу тяготения, действующую со стороны Земли на тело массой 1 кг, находящееся на поверхности Луны. Расстояние между центрами Земли и Луны принять равными 384 000 км.

Задача 147. Спутник делает 16 оборотов за время одного оборота Земли. Определить период, высоту и скорость спутника, считая его орбиту круговой.

Задача 148. Трамвайный вагон массой 5 тонн идет по закруглению радиусом 128 м. Найти силу бокового давления колес на рельсы при скорости движения 9 км/ч.

Задача 149. Гирька, привязанная к нити длиною 30 см, описывает в горизонтальной плоскости окружность радиусом 15 см. Какому числу оборотов в минуту соответствует скорость вращения гирьки? (59 об/мин)

Задача 150. Шарик на веревке длиной 50 см равномерно вращается в вертикальной плоскости. Найти, при какой частоте вращения веревка оборвется, если предел прочности веревки mg, где m - масса шарика.

Задача 151. Мотоциклист едет по горизонтальной дороге со скоростью 72 км/ч, делая поворот радиусом кривизны в 100 м. Насколько при этом он должен накрениться, чтобы не упасть при повороте?

Задача 152. Шоссе имеет вираж с уклоном в 10° при радиусе закругления дороги в 100 м. На какую скорость рассчитан вираж?

Задача 153. Средняя высота спутника над поверхностью Земли 1700 км. Определить его скорость и период вращения.

Задача 154. С увеличением высоты полета спутника его скорость уменьшилась с 7,79 до 7,36 км/с. Определить, на сколько изменились период вращения спутника и удаленность его от земной поверхности.

Задача 155. Определить период вращения искусственного спутника вблизи планеты, которую можно принять за однородный шар плотностью ρ.

Задача 156. Спутник вывели на круговую орбиту со скорость v  над полюсом Земли. Найти расстояние от спутника до поверхности Земли.

Задача 157. Найти массу Земли, если спутник, движущийся в ее экваториальной плоскости с запада на восток по круговой орбите радиуса R=2∙104 км, появляется над некоторым пунктом на экваторе через каждые τ=11,6 ч.

Задача 158. Подводная лодка, не имевшая хода, получив небольшую плавучесть р = 0.01mg, начинает подниматься с глубины H=100 м. При этом начавший работать двигатель обеспечивает постоянную горизонтальную силу тяги Т = 0,01mg . Силу сопротивления принять пропорциональной первой степени скорости V и равной R = –0,1mV . Определить траекторию лодки и расстояние, пройденное ею по горизонтали к моменту всплытия.

Задача 159. Определить закон движения x (t), y (t) тяжелой материальной точки M массы m = 5 кг, притягиваемой к неподвижному центру O силой, прямо пропорциональной расстоянию до него. Движение происходит в пустоте, сила притяжения F=-k2mOM, k = 20 с–1. Ускорение свободного падения g = 9,8 м/с2. В начальный момент времени (t=0) , vx0 = 200 м/с, . Ось Ox горизонтальна, а ось Oy направлена по вертикали вверх.

Задача 160. Подводная лодка, не имевшая хода, находилась в надводном положении на расстоянии H=100 м от дна. Получив отрицательную плавучесть р = 0.1mg, она начинает уходить от преследования на очень тихом ходу, который обеспечивается малой постоянной горизонтальной силой тяги двигателя T = 0,001mg. Горизонтальной компонентой силы сопротивления можно пренебречь, а ее вертикальную составляющую принять равной R = –0.05mg, где Vy – вертикальная скорость погружения лодки. Определить закон движения лодки и расстояние, пройденное ею по горизонтали к моменту, когда она ляжет на дно.

Задача 161. Точка M массы m = 5 кг движется под действием силы отталкивания от неподвижного центра O, изменяющейся по закону F=k2mr, где k = 20 c–1, r – радиус-вектор точки. В начальный момент точка M имела координаты M0 (a,0), a = 24 м, и скорость v0 с проекциями vx0 = 0, vy0 = 4 м/с. Определить закон движения и траекторию точки M. Силой тяжести Земли пренебречь.

Задача 162. Подводная лодка, не имевшая хода, получив небольшую положительную плавучесть р = 0,001mg, начинает подниматься с глубины H=150 м. При этом начавший работать двигатель обеспечивает постоянную горизонтальную силу тяги T=mg. Вертикальной компонентой силы сопротивления можно пренебречь, а ее горизонтальную составляющую принять равной , где Vx – горизонтальная скорость лодки. Определить траекторию движения лодки и расстояние, пройденное ею по горизонтали к моменту всплытия.

Задача 163. Подводная лодка, двигавшаяся в надводном положении c малой скоростью U0 = 0,5 м/с, получив отрицательную плавучесть р = 0,5mg, начала срочное погружение с выключенными двигателями. Горизонтальной компонентой силы сопротивления можно пренебречь, а ее вертикальную составляющую принять равной R = –0,05mg, где Vy – вертикальная скорость погружения лодки. Определить закон движения лодки и расстояние, пройденное ею по горизонтали к моменту, когда она погрузится на глубину H=150 м.

Задача 164. Телу M массы m = 8 кг, принимаемому за материальную точку и находящемуся на гладкой наклонной плоскости с углом наклона к горизонту  = 30° (рис. 4), сообщена начальная скорость v0 = 18 м/с, направленная под углом  = 45° к оси x и лежащая в плоскости ху. Ось y горизонтальна. Ускорение свободного падения g = 9,8 м/с2. Определить закон движения тела по наклонной плоскости x (t), y (t).

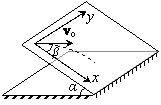
image916

Рис.4

 

Задача 165. Подводная лодка, двигавшаяся в надводном положении со скоростью U0 = 0,5 м/с, получив отрицательную плавучесть р = 0,1mg, начала погружение с выключенными двигателями. Силу сопротивления принять пропорциональной первой степени скорости V и равной R=-0,05mV. Определить траекторию движения лодки и расстояние, пройденное ею по горизонтали к моменту, когда она погрузится на глубину H=150 м.

Задача 166. Наибольшая горизонтальная дальность полета снаряда  м  достигается при угле бросания  по отношению к горизонту. Определить, чему равны начальная скорость снаряда v0 и. Ускорение свободного падения g = 9,8 м/с2. Сопротивлением воздуха пренебречь. Начальная скорость снаряда v0 при вылете из канала ствола орудия фиксирована.

Задача 167. Береговое орудие, расположенное на высоте H=150 м над уровнем моря, стреляет снарядами, имеющими при вылете из ствола скорость U0 = 1500 м/с. Определить дальность поражения цели при горизонтальном выстреле и закон движения снаряда x (t), y (t), если вертикальной компонентой силы сопротивления можно пренебречь, а ее горизонтальную составляющую принять равной , где Vx – горизонтальная скорость снаряда.

Задача 168. Определить закон движения x (t), y (t) материальной точки M массы m = 8 кг, притягиваемой к неподвижному центру O силой, прямо пропорциональной расстоянию до него. Движение происходит в пустоте, сила притяжения равна F=-k2mOM, k = 12 c–1. В начальный момент времени (t=0) х0 = 18 м, , vy0 = 6 м/с. Силой тяжести Земли пренебречь.

Задача 169. Материальная точка массы m движется по гладкой горизонтальной плоскости Oxy под действием силы, направленной параллельно оси x. Модуль силы изменяется по закону F=3t2. Начальная скорость  м/с направлена под углом  к линии действия силы. Получить уравнение траектории точки y (x).

Задача 170. Точка M массы m = 8 кг движется под действием силы отталкивания от неподвижного центра O, изменяющейся по закону F=k2mr, где k = 12 c–1, r – радиус-вектор точки. Ускорение свободного падения g = 9.8 м/с2. В начальный момент времени (t=0) х0 = 20 м, , vy0 = 50 м/с. Ось Ox горизонтальна, а ось Oy направлена по вертикали вверх. Определить закон движения x (t), y (t) и траекторию y (x) точки M.

Задача 171. Материальная точка массы m движется по гладкой горизонтальной плоскости Oxy под действием силы, направленной параллельно оси у (см. рис. 39). Модуль силы изменяется по закону F=4t3. Начальная скорость V0=5 м/с направлена перпендикулярно к линии действия силы. Найти закон движения x (t), y (t) и уравнение траектории точки y = y (x).

Задача 172. Телу M массы m = 20 кг, принимаемому за материальную точку и находящемуся на гладкой наклонной плоскости с углом наклона к горизонту  = 60° (см. рис. 39), сообщена начальная скорость v0 = 2 м/с, направленная под углом  = 30° к оси x и лежащая в плоскости ху. Ось y горизонтальна. Ускорение свободного падения g = 9,8 м/с2. Определить закон движения тела по наклонной плоскости x (t), y (t).

Задача 173. При угле бросания  = 60° по отношению к горизонту снаряд имеет горизонтальную дальность полета  м. Определить, чему при этом равна начальная скорость снаряда v0. Найти также горизонтальную дальность и  максимальную высоту траектории при угле бросания 30°. Ускорение свободного падения g = 9,8 м/с2. Сопротивлением воздуха пренебречь. Начальная скорость снаряда v0 при вылете из канала ствола орудия фиксирована.

Задача 174. Определить закон движения x (t), y (t) тяжелой материальной точки M массы m = 6 кг, притягиваемой к неподвижному центру O силой, прямо пропорциональной расстоянию до него. Движение происходит в пустоте, сила притяжения равна F=-k2mOM, k = 8 c–1. Ускорение свободного падения g = 9.8 м/с2. В начальный момент времени (t=0) х0 = 24 м, Vx0=0, у0 = 40 м, Vy0=0. Ось Ox горизонтальна, а ось Oy направлена по вертикали вверх.

Задача 175. Точка M массы m = 4 кг движется под действием силы отталкивания от неподвижного центра O, изменяющейся по закону F=k2mr, где k = 10 c–1, r – радиус-вектор точки. Ускорение свободного падения g = 9,8 м/с2. В начальный момент времени (t=0)  х0 = 2 м, vх0 = 4 м/с, . Ось Ox горизонтальна, а ось Oy направлена по вертикали вверх. Определить закон движения x (t), y (t) и траекторию y (x) точки M.

Задача 176. Парашютист массы m падает с раскрытым парашютом на Землю в спокойном воздухе вертикально с установившейся постоянной скоростью V0=5 м/с. На высоте h=100 м над поверхностью Земли он, натянув стропы, приобретает горизонтальную скорость  м/с. Определить величину горизонтального отклонения парашютиста от первоначального направления его движения в момент приземления и закон его движения, если при дальнейшем спуске он удерживает стропы в том же положении. Горизонтальная компонента силы сопротивления, действующая на парашютиста в воздушном потоке, Rx = –0,01mVx, где Vx – горизонтальная скорость парашютиста. Изменением вертикальной компоненты силы сопротивления, вызванной наклоном купола парашюта, пренебречь.

Задача 177. Стартуя с поверхности Земли, реактивный снаряд массы M=100 кг движется в течение первых 10 с под действием силы тяги F=5000 H, направленной под углом  к горизонту (). Затем сила тяги отключается. Определить траекторию движения снаряда и его дальность полета. Силой сопротивления воздуха пренебречь.

Задача 178. Телу M массы m = 28 кг, принимаемому за материальную точку и находящемуся на гладкой наклонной плоскости с углом наклона к горизонту  = 45° (см. рис. 39), сообщена начальная скорость v0 = 34 м/с, направленная под углом  = 30° к оси x и лежащая в плоскости ху. Ось y горизонтальна. Ускорение свободного падения g = 9,8 м/с2. Определить закон движения тела по наклонной плоскости x (t), y (t).

Задача 179. Подводная лодка, не имевшая хода, получив небольшую положительную плавучесть p = 0.01mg, начинает подниматься с глубины H=100 м. При этом начавший работать двигатель обеспечивает постоянную горизонтальную силу тяги Т = 0.01mg. Вертикальной компонентой силы сопротивления можно пренебречь, а ее горизонтальную составляющую принять равной R = –0.01mVx, где Vx – горизонтальная скорость лодки. Определить траекторию движения лодки y (x) и расстояние, пройденное ею по горизонтали к моменту всплытия.

Задача 180. При угле бросания  = 42° по отношению к горизонту снаряд имеет горизонтальную дальность полета  м. Определить, чему равна начальная скорость снаряда v0 при вылете из канала ствола орудия. Найти также горизонтальную дальность полета снаряда и время полета снаряда до цели при угле бросания  = 35° и той же начальной скорости v0. Ускорение свободного падения g = 9,8 м/с2. Сопротивлением воздуха пренебречь.

Задача 181. Определить угол наклона  ствола орудия к горизонту, чтобы поразить цель, обнаруженную на той же горизонтальной плоскости, что и орудие, на расстоянии  м. Дополнительно определить максимальную высоту траектории и время полета снаряда до цели. Начальная скорость снаряда v0 = 600 м/с. Ускорение свободного падения g = 9.8 м/с2. Сопротивлением воздуха пренебречь.

Задача 182. Определить зависимость горизонтальной дальности полета снаряда , максимальной высоты его траектории  и времени полета  от угла наклона  ствола орудия к горизонту. Найти также значения этих величин для  = 38°. Начальная скорость снаряда v0 = 980 м/с. Ускорение свободного падения g = 9,8 м/с2. Сопротивлением воздуха пренебречь.

Задача 183. Шарик m=0,5 кг, привязан к нити l=0,7 м. Нить вместе с шариком вращается в вертикальной плоскости, затрачивая на один оборот 1 с. Определить натяжение нити в моменты высшего и низшего положения шарика.

Задача 184. Самолет летит на высоте 4000 м над землей с горизонтальной скоростью 140 м/с (рис.5). На каком расстоянии х, должен быть сброшен с самолета без начальной скорости (относительной) груз для того, чтобы он упал в эту точку?

Безымянный

Рис.5

 

Задача 185. Материальная точка m=2 кг движется в плоскости Оxy согласно уравнениям x=sinπt, y=0,5t2. Определить модуль количества движения точки в момент времени t=1,5 с.

Задача 186. Материальная точка m=8 кг движется в плоскости Оxy согласно уравнениям x=0,05t3, y=0,3t2. Определить модуль равнодействующих приложенных к точке сил в момент t =4c.

Задача 187. Материальная точка массы m движется в плоскости 0ху согласно уравнениям х = а cosωt, у = b sinωt. Найти силу, действующую на точку.

Задача 188. Решето рудообогатительного грохота совершает вертикальные гармонические колебания с амплитудой b= 5 см. Найти наименьшую частоту ω колебаний решета, при котором куски руды, лежащие на нем, отделяются от него и подбрасывают вверх.

Задача 189. Автомобиль массы m = 1500 кг движется по выпуклому участку дороги со скоростью v = 10 м/с. Радиус кривизны в верхней точке дороги р = 60 м. Определить силу давления автомобиля на дорогу в момент прохождения этого участка дороги.

Задача 190. Автомобиль массы m = 1500 кг движется по вогнутому участку дороги со скоростью v = 15 м/с. Радиус кривизны в нижней точке дороги р = 80 м. Определить силу давле­ния автомобиля на дорогу в момент прохождения этого участка дороги.

Задача 191. Гиря массы r = 0,3 кг подвешена к нити длиной l = 1 м; вследствие толчка гиря получила горизонтальную скорость v = 3 м/с. Найти натяжение нити непосредственно после толчка.

Задача 192. Груз, привязанный к нити длиной l = 0,5 м, движется по окружности в вертикальной плоскости. Какую минимальную скорость в наивысшем положении должен иметь груз, чтобы нить оставалась натянутой.

Задача 193. Груз массы m = 0,2 кг, подвешенный на нити l = 0,4 м в неподвижной точке О, представляет собой конический маятник, то есть описывает окружность в горизонтальной плоскости, причем нить составляет с вертикалью угол α = 30°. Определить скорость груза и натяжение нити.

Задача 194. Искусственный спутник Земли описывает круговую орбиту радиуса R на небольшой высоте над поверхностью Земли (изменением силы тяжести на этой высоте по сравнению с силой тяжести на поверхности Земли можно пренебречь). Определить скорость движения спутника по орбите и время одного оборота спутника. Радиус Земли R = 6380 км.

Задача 195. Вал двигателя вращается с угловой скоростью ω=90е-20t+85(1-e-20t). Определить главный момент внешних сил, действующих на вал, в момент времени t=0,1 c, если его момент инерции относительно оси вращения равен 1 кг∙м2.

Задача 196. Ротору массой 314 кг и радиусом инерции ρ=1 м, сообщена угловая скорость ω0=10 с-1. Предоставленный самому себе, он остановился, сделав 100 оборотов. Определить момент трения в подшипниках, считая его постоянным.

Задача 197. Камень массы 0,3 кг, привязанный к нити длины 1 м, описывает окружность в вертикальной плоскости. Определить наименьшую угловую скорость камня, при которой произойдет разрыв нити, если ее сопротивление разрыву 9 Н.

Задача 198. Шлифовальный круг ∅=0,6 м делает 120 об/мин. Потребляя мощность 1,2 кВт. Коэффициент трения шлифовального круга о деталь 0,2. С какой силой круг прижимается к детали?

Задача 199. Материальная точка m=22 кг, движется по окружности R=10 м согласно уравнению S=0,3t2. Определить модуль равнодействующих сил, действующих на точку, в момент времени t=5 с.

Задача 200. Материальная точка m=18 кг, движется по окружности R=8 м согласно уравнению S=е0,3t. Определить проекцию равнодействующих сил, приложенных к точке, на касательную к траектории в момент времени t=10 c.

Задача 201*. Считая Землю шарообразной, найти зависимость ускорения силы тяжести Земли от широты местности. Вычислить g на полюсе, экваторе и на широте Одессы

Задача 202*. Найти изменение ускорения силы тяжести тела на глубине h от поверхности Земли. На какой глубине ускорение силы тяжести составит 0,3 от ускорения силы тяжести на поверхности Земли? Плотность земли считать постоянной. Считать, что со стороны вышележащего слоя тело не испытывает никакого притяжения.

Задача 203*. Воздушный шар массы m под действием выталкивающей силы F = 1.1mg начинает подъем. Горизонтальная компонента силы сопротивления воздуха пропорциональна квадрату горизонтальной компоненты скорости шара относительно воздуха: Rx = –0.1m, где Vx – его горизонтальная относительная скорость. Вертикальной компонентой силы сопротивления воздуха пренебречь. Определить закон движения шара x (t), y (t), если дует горизонтальный ветер со скоростью  м/с.

Задача 204*. Тело M массы m = 8 кг находится под действием двух сил притяжения F1=-k2mO1M, F2=-k2mO2M, k = 20 c–1, направленных к двум неподвижным центрам O1 (–a,0) и O2 (a,0), a = 24 м. Движение начинается в точке A0 (–2a,0) со скоростью Vx0=0, vу0 = 18 м/с. Определить закон движения x (t), y (t) и траекторию y (x) точки M. Найти моменты времени, когда она пересекает ось Ox, и вычислить ее координаты в эти моменты времени. Силой тяжести пренебречь.

Задача 205*. Тело M массы m = 2 кг находится под действием двух сил притяжения F1=-k2mO1M, F2=-k2mO2M, k = 120 c–1, направленных  к  двум  неподвижным  центрам O1 (–a,0) и O2 (a,0), а = 12 м. Ускорение свободного падения g = 9.8 м/с2. Движение начинается в точке A0 (2a,0) со скоростью Vx0=0, vу0 = 12 м/с. Ось Ox горизонтальна, а ось Oy направлена по вертикали вверх. Определить закон движения x (t), y (t) и траекторию y (x) точки M. Найти моменты времени, когда она пересекает ось Ox, и вычислить ее координаты в эти моменты времени.

Задача 206*. Материальная точка M массы m движется в вертикальной плоскости под действием силы тяжести, постоянной горизонтальной силы тяги F = 0.1mg, силы сопротивления R= –0.1mV, где V – скорость точки, и вертикальной подъемной силы Q = 2mvx, где Vx – горизонтальная скорость точки. Получить закон движения точки вдоль вертикальной оси y, если в начальный момент времени (t=0) ее положение совпадало с началом системы координат, а ее начальная скорость горизонтальна и равна V0=5 м/с.

Задача 207*. Тело массы m на высоте H=500 м над поверхностью Земли имело скорость V0=7 м/с, направленную вертикально вниз. Затем оно попадает в воздушный поток, который движется горизонтально с постоянной скоростью  м/с. В результате на него действует сила  где Vr – скорость тела относительно потока. Определить величину горизонтального отклонения тела от первоначального направления его движения в момент падения на Землю.

Задача 208*. Парашютист массы m, совершая затяжной прыжок, падает на Землю в спокойном воздухе вертикально с установившейся постоянной скоростью V0=40 м/с. На некоторой высоте от поверхности Земли он попадает в воздушный поток, который движется горизонтально с постоянной скоростью u0 = 0.5 м/с, и в это же время открывает парашют. Горизонтальная компонента силы, действующая на парашютиста в воздушном потоке, Rx = –0.01mVrx, где Vrx – горизонтальная скорость тела относительно потока воздуха. Вертикальная компонента силы сопротивления, действующая на парашютиста, Ry = –0.1m, где Vy – его вертикальная скорость. Определить закон движения парашютиста x (t), y (t) после раскрытия парашюта.

Задача 209*. Материальная точка M массы m движется в вертикальной плоскости под действием силы тяжести, постоянной горизонтальной силы тяги F = 0.2mg, силы сопротивления R = –0.1mV, где V – скорость точки, и вертикальной подъемной силы Q=2mVx, где Vx – горизонтальная скорость точки. Получить закон движения точки в направлении горизонтальной оси x, если в начальный момент времени (t=0) ее положение совпадало с началом системы координат, а ее начальная скорость горизонтальна и равна V0=5  м/с.

Задача 210*. Парашютист массы m с раскрытым парашютом падает вертикально с установившейся постоянной скоростью V0=5 м/с. На высоте h=100 м над поверхностью Земли он попадает в воздушный поток, который движется горизонтально с постоянной скоростью  м/с. Определить величину горизонтального отклонения парашютиста от первоначального направления его движения в момент приземления и закон его движения x (t), y (t). Горизонтальная компонента силы сопротивления, действующая на парашютиста в воздушном потоке, Rх = –0.01mVx, где Vx – горизонтальная скорость парашютиста относительно потока воздуха.

 

3. Относительное движение материальной точки

Задача 211.  Тело 1 вращается относительно оси ОХ1 с постоянной угловой скоростью ωe (рис.6). По гладкому каналу, выполненному в теле 1, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

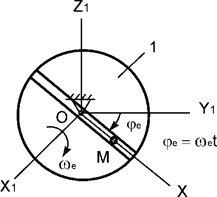
Билет 1

Рис.6

 

Задача 212.  Тело 1 вращается относительно оси О1Z1 с постоянной угловой скоростью ωe (рис.7). По гладкому каналу, выполненному в теле 1, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

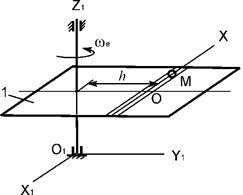
Билет 2

Рис.7

 

Задача 213.  Тело 1 вращается относительно оси О1Z1 с постоянной угловой скоростью ωe (рис.8). По гладкому каналу, выполненному в теле 1, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

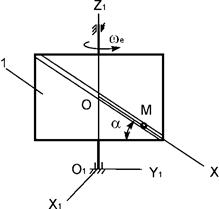
Билет 3

Рис.8

 

Задача 214.  Тело 1 вращается относительно оси О1Z1 с постоянной угловой скоростью ωe (рис.9). По гладкому каналу, выполненному в теле 1, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

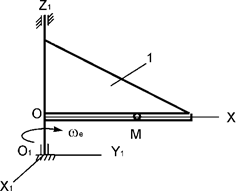
Билет 4

Рис.9

 

Задача 215.  Тележка 1 совершает поступательное горизонтальное движение по закону y1 = 4t3 + 2t2 + t + 1, м (рис.10). В гладком наклонном канале тележки перемещается шарик M массой m. Записать дифференциальное уравнение относительного движения точки М.

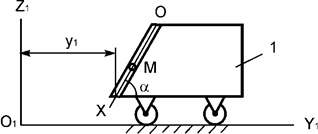
Билет 5

Рис.10

 

Задача 216.  Плоский механизм состоит из трех тел (рис.11). Тела 1, 2 имеют одинаковые размеры (O1A = O2B = r1 = r2 = r = 1 м) и совершают вращательные движения с постоянными угловыми скоростями ω1 = ω2 = ω. По гладкому каналу, выполненному в теле 3, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

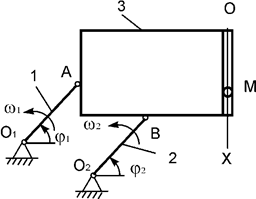
Билет 6

Рис.11

 

Задача 217.  Горизонтальная пластина вращается относительно оси О1Z1 с постоянной угловой скоростью ωe (рис.12). По гладкому каналу, выполненному на пластине, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

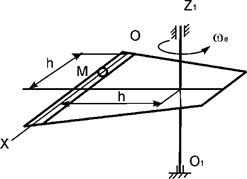
Билет 7

Рис.12

 

Задача 218. Пластина совершает поступательное движение параллельно оси О1Z1 согласно уравнению z1 = 20sinπt (рис.13). По каналу, выполненному на пластине, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

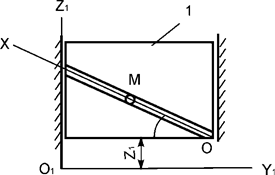
Билет 8

Рис.13

 

Задача 219. Тележка 1 совершает поступательное горизонтальное движение по закону y1 = 4t3 + 2t2 + t + 1, м (рис.14). В гладком наклонном канале тележки перемещается шарик М массой m. Записать дифференциальное уравнение относительного движения точки М.

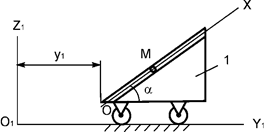
Билет 9

Рис.14

 

Задача 220. Вертикальная пластина вращается относительно оси О1Z1 с постоянной угловой скоростью ωe (рис.15). По гладкому каналу, выполненному на пластине, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

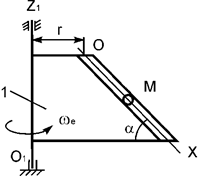
Билет 10

Рис.15

 

Задача 221. Вертикальная пластина вращается относительно оси О1Z1 с постоянной угловой скоростью ωe (рис.16). По гладкому каналу, выполненному на пластине, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

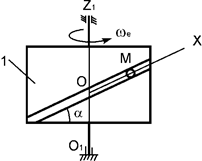
Билет 11

Рис.16

 

Задача 222. Вертикальная пластина 1 вращается относительно оси О1Х1 с постоянной угловой скоростью ω1 = ωe (рис.17). По гладкому каналу, выполненному на пластине, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

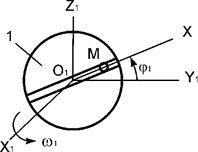
Билет 12

Рис.17

 

Задача 223. Пластина совершает поступательное движение параллельно оси О1Z1 согласно уравнению z1 = 20sinπt (рис.18). По гладкому каналу, выполненному на пластине, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

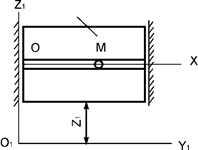
Билет 13

Рис.18

 

Задача 224. Вертикальная пластина 1 вращается относительно оси О1Z1 с постоянной угловой скоростью ω1 = ωe (рис.19). По гладкому каналу, выполненному на пластине, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

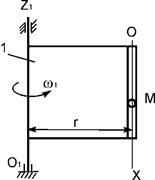
Билет 14

Рис.19

 

Задача 225. Вертикальная пластина 1 вращается относительно оси О1Х1 с постоянной угловой скоростью ω1 = ωe (рис.20). По гладкому каналу, выполненному на пластине, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

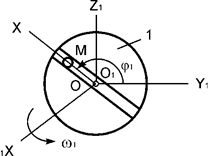
Билет 15

Рис.20

 

Задача 226. Тележка 1 совершает поступательное горизонтальное движение по закону y1 = 4t3 + 2t2 + t +1, м (рис.21). В гладком наклонном канале тележки перемещается шарик М массой m. Записать дифференциальное уравнение относительного движения шарика.

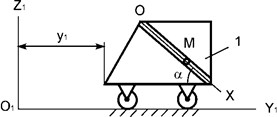
Билет 16

Рис.21

 

Задача 227. Пластина совершает поступательное движение параллельно оси  О1Y1 согласно уравнению y1 = 20sinπt (рис.22). По гладкому каналу, выполненному на пластине, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

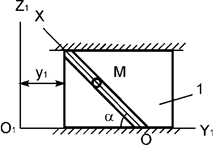
Билет 18

Рис.22

 

Задача 228. Тележка 1 совершает поступательное горизонтальное движение по закону y1 = 4t3 + 2t2 + t +1, м (рис.23). В гладком наклонном канале тележки перемещается шарик М массой m. Записать дифференциальное уравнение относительного движения точки М.

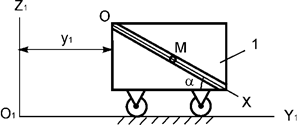
Билет 19

Рис.23

 

Задача 229. Вертикальная пластина 1 вращается относительно оси О1Z1 с постоянной угловой скоростью ω1 = ωe (рис.24). По гладкому каналу, выполненному на пластине, перемещается точка М массой m. Записать дифференциальное уравнение относительного движения точки М.

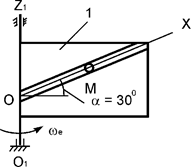
Билет 20

Рис.24

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

 

Строительная механика   Сопротивление материалов

Прикладная механика  Детали машин  Теория машин и механизмов

 

 

 

00:00:00

 

Top.Mail.Ru