Главная

Лекция 6 (продолжение). Задачи для самостоятельного решения.

Задача 1. Пуля массой m ударяется о баллистический маятник массой М и застревает в нем. Какая доля кинетической энергии пули перейдет в теплоту?

Задача 2. Камень, пущенный по поверхности льда со скоростью 2 м/с, прошел до полной остановки расстояние 20,4 м. Найти коэффициент трения камня по льду, считая его постоянным.

Задача 3. Вагон массой 20 тонн, движущийся равнозамедленно, под действием силы трения в 6000 Н через некоторое время останавливается. Начальная скорость вагона равна 54 км/ч. Найти: 1) работу сил трения, 2) расстояние, которое вагон пройдет до остановки.

Задача 4. Камень массой 2 кг упал с некоторой высоты. Падение продолжалось 1,43 с. Найти кинетическую и потенциальную энергию в средней точке пути. Сопротивлением воздуха пренебречь.

Задача 5. С башни высотой 25 м горизонтально брошен камень со скоростью 15 м/с. Найти кинетическую и потенциальную энергию камня спустя одну секунду после начала движения. Масса камня 0,2 кг.

Задача 6. Камень бросили под углом 60° к горизонту со скоростью 15 м/с. Найти кинетическую, потенциальную и полную энергию камня: 1) спустя одну секунду после начала движения, 2) в высшей точке траектории. Масса камня 0,2 кг. Сопротивлением воздуха пренебречь.

Задача 7. Работа, затраченная на толкание ядра, брошенного под углом 30° к горизонту, равна 216 Дж. Через сколько времени и на каком расстоянии от места бросания ядро упадет на землю? Масса ядра 2 кг. Сопротивлением воздуха пренебречь.

Задача 8. Сила тяги автомобиля изменяется с расстоянием по законам: а) F=D+Bs; б) F=D+Bs+Сs². Определить работы силы на участке пути (s₁, s₂).

Задача 9. По наклонной плоскости высотой 0,5 м и длиною склона 1 м скользит тело массой в 3 кг. Тело приходит к основанию наклонной плоскости со скоростью 2,45 м/с. Найти: 1) коэффициент трения тела о плоскость, 2) количество тепла, выделенного при трении. Начальная скорость тела равна нулю.

Задача 10. К концу тонкой нерастяжимой нити, намотанной на цилиндрический сплошной неподвижный блок массой m₁=200 г, прикреплено тело массой m₂=500 г, которое находится на наклонной плоскости с углом наклона α=45°. Нить, удерживающая тело, параллельна наклонной плоскости. Какой путь пройдет тело по наклонной плоскости за t=1 с, если коэффициент трения скольжения по наклонной плоскости μ=0,1.

Задача 11. Какую работу нужно совершить, чтобы маховику в виде диска массой m=100 кг и радиусом R=0,4 м сообщить частоту вращения n=10 об/с, если он находится в состоянии покоя?

Задача 12. Обруч и диск имеют одинаковую массу и катятся без скольжения с одинаковой линейной скоростью. Кинетическая энергия обруча равна 39,2 Дж. Найти кинетическую энергию диска.

Задача 13. Медный шар радиусом R=10 см вращается со скоростью, соответствующей v=2 об/с, вокруг оси, проходящей через его центр. Какую работу надо совершить, чтобы увеличить угловую скорость вращения шара вдвое.

Задача 14. Вентилятор вращается со скоростью, соответствующей 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 75 об. Работа сил торможения равна 44,4 Дж. Найти: 1) момент инерции вентилятора, 2) момент силы торможения.

Задача 15. Маховик вращается с постоянной скоростью, соответствующей n=10 об/с; его кинетическая энергия Е_к = 800 Дж. За сколько времени вращающий момент сил М=50 Н∙м, приложенный к этому маховику, увеличит угловую скорость маховика в два раза?

Задача 16. Танк, масса которого 15 т и мощность 368 кВт, поднимается в гору с уклоном 30°. Какую максимальную скорость может развивать танк?

Задача 17. Найти линейные ускорения движения центров тяжести 1) шара, 2) диска и 3) обруча, скатывающихся без скольжения с наклонной плоскости. Угол наклона плоскости равен 30°, начальная скорость всех тел равна нулю. 4) Сравнить найденные ускорения с ускорением тела, соскальзывающего с этой наклонной плоскости при отсутствии трения.

Задача 18. Найти линейные скорости движения центров тяжести 1) шара, 2) диска и 3) обруча, скатывающихся без скольжения с наклонной плоскости. Высота наклонной плоскости 0,5 м, начальная скорость всех тел равна нулю. 4) Сравнить найденные скорости со скоростью тела, соскальзывающего с этой наклонной плоскости при отсутствии трения.

Задача 19. Люстра массой 100 кг подвешена к потолку на металлической цепи, длина которой 5 м. Какова высота, на которую можно отклонить люстру, чтобы при последующих качаниях цепь не оборвалась, если известно, что разрыв наступает при силе натяжения 2 кН?

Задача 20. Груз 1 массы m₁, опускаясь вертикально вниз (рис.1), раскручивает ступенчатый блок 2 посредством невесомой и нерастяжимой нити, которая намотана на колесо блока радиуса r₁. На большее колесо блока, имеющее радиус r₂, намотана другая нить, второй конец которой привязан к грузу 3 массы m, скользящему по наклонной плоскости с коэффициентом трения скольжения f и углом наклона . Блок состоит из однородных дисков массами и соответственно, жестко соединенных друг с другом и имеющих общую ось вращения. Определить скорость груза 3 в зависимости от пройденного им расстояния и его ускорение, если движение начинается из состояния покоя.

Рис.1

Задача 21. Каток (рис.2) 1 массы m и радиуса r катится без скольжения под действием силы F по горизонтальной плоскости и поднимает груз 2 массы m₁ при помощи невесомой нити, переброшенной через блок 3, который имеет такие же, как и каток, массу и радиус. Определить скорость груза 2 в зависимости от пройденного им расстояния и его ускорение, если коэффициент трения качения k, участок нити АВ горизонтален, а движение начинается из состояния покоя.

Рис.2

Задача 22. Груз 1, (рис.3) падая по вертикали, раскручивает ступенчатый блок 3 посредством невесомой и нерастяжимой нити, которая намотана на колесо блока радиуса r₁. На меньшее колесо блока, имеющее радиус r₂, намотана другая нить, второй конец которой привязан к оси цилиндрического катка, катящегося без скольжения. Масса груза m₁, масса катка m₂, коэффициент трения качения k, радиус катка r. Пренебрегая массой блока, определить скорость груза 1 в зависимости от пройденного им расстояния и его ускорение, если участок нити АВ горизонтален, а движение начинается из состояния покоя.

Рис.3

Задача 23. Кривошип ОА гипоциклического механизма (рис.4), расположенного в горизонтальной плоскости, вращался с постоянной угловой скоростью . В некоторый момент времени двигатель был отключен и под действием постоянного момента М₀ сил сопротивления на оси сателлита (подвижной шестерни 1) механизм остановился. Определить угол поворота кривошипа до остановки, если его масса равна m₀, масса сателлита m, r₁ – его радиус, а r – радиус неподвижной шестерни 2. Кривошип принять за однородный тонкий стержень, сателлит – за однородный диск.

Рис.4

Задача 24. Блоки радиусами r₁ и r₂ (рис.5) жестко скреплены между собой и насажены на общую ось. Грузы 1 и 2 массами m₁ и m₂, разматывая нити, намотанные на блоки, приводят их во вращение. При вращении на блоки действует постоянный момент сил сопротивления М. Пренебрегая массой нитей и считая блоки однородными дисками массами М₁ и М₂ соответственно, определить скорость v₁ груза 1 как функцию пройденного им расстояния и его ускорение, если движение начинается из состояния покоя.

Рис.5

Задача 25. Блоки радиусами r₁ и r₂ (рис.6) жестко скреплены между собой и насажены на общую ось. Грузы 1 и 2 массами m₁ и m₂, разматывая нити, намотанные на блоки, приводят их во вращение. При вращении на блоки действует момент сил сопротивления , где a – постоянная, а – угол поворота. Пренебрегая массой нитей и считая блоки однородными дисками массами М₁ и М₂ соответственно, определить угловую скорость и угловое ускорение блоков как функции угла поворота , а также момент времени, когда система под действием сил сопротивления остановится, если движение начинается из состояния покоя.

Рис.6

Задача 26. К грузам А и В (рис.7) массами m₁ и m₂ соответственно прикреплены нерастяжимые нити, вторые концы которых намотаны на однородные диски 1 и 2 массами и радиусами r₁ и r₂ (r₂ > r₁). Диски жестко соединены между собой и насажены на общую ось. Груз А, спускаясь по наклонной плоскости с углом наклона к горизонту, раскручивает диски и поднимает груз В вверх по наклонной плоскости с углом . Определить скорость груза А в зависимости от пройденного им расстояния и его ускорение. Силами трения и массой нитей пренебречь.

Рис.7

Задача 27. Кривошип BА (рис.8) гипоциклического механизма, расположенного в горизонтальной плоскости, вращался с постоянной угловой скоростью . В некоторый момент времени двигатель был отключен и под действием постоянных моментов М_В и М_А сил сопротивления на оси сателлита (подвижной шестерни 1) и на оси кривошипа механизм остановился. Определить угол поворота кривошипа до остановки, если его масса равна m₀, масса сателлита m, r₀ – его радиус, а r – радиус неподвижной шестерни 2. Кривошип принять за однородный тонкий стержень, сателлит – за однородный диск.

Рис.8

Задача 28. Зубчатые колеса 1 и 2 (рис.9), насаженные на неподвижные параллельные оси О₁ и О₂, имеют внутреннее зацепление. Колесо 1 является однородным диском и имеет радиус r₁ и массу m₁, а колесо 2 – радиус r₂, а его масса m₂ распределена по ободу равномерно. На колесо 2 намотана невесомая нить, к концу которой прикреплен опускающийся груз 3 массы m₃. Пренебрегая трением и считая, что движение начинается из состояния покоя, определить угловую скорость колеса 2 в зависимости от его угла поворота, а также его угловое ускорение.

Рис.9

Задача 29. К грузам А и В массами m₁ и m₂ (рис.10) соответственно прикреплены нерастяжимые нити, вторые концы которых намотаны на однородные диски 1 и 2 массами и радиусами r₁ и r₂ (r₂ > r₁). Диски жестко соединены между собой и насажены на общую ось. Груз B, спускаясь по наклонной плоскости с углом наклона к горизонту, раскручивает диски и поднимает груз A вверх по наклонной плоскости с углом . В блоке действует постоянный момент сил сопротивления М. Определить скорость груза В в зависимости от пройденного им расстояния и его ускорение. Силами трения и массой нитей пренебречь.

Рис.10

Задача 30. Зубчатые колеса 1 и 2 (рис.11), насаженные на неподвижные параллельные оси О₁ и О₂, имеют внутреннее зацепление. Колесо 1 радиуса r₁ и массы m₁, начальная угловая скорость которого равна нулю, приводится в движение вращающим моментом , где a – постоянная, а – угол поворота колеса 1. Масса m₂ колеса 2 распределена по ободу равномерно. Считая колесо 1 однородным диском и пренебрегая трением, определить его угловую скорость в зависимости от , а также его угловое ускорение.

Рис.11

Задача 31. Блоки радиусами r₁ и r₂ (рис.12) жестко скреплены между собой и насажены на общую ось. Груз 2 массы m₂, разматывая намотанную на блок нить, приводит блоки во вращение и поднимает груз 1 массы m₁. При вращении на блоки действует постоянный момент сил сопротивления М. Пренебрегая массой нитей и считая блоки однородными дисками массами М₁ и М₂ соответственно, определить скорость груза 2 v₂ как функцию пройденного им расстояния и его ускорение, если движение начинается из состояния покоя.

Рис.12

Задача 32. Через блоки 1, 2 и 3 (рис.13) переброшена невесомая нерастяжимая нить, к одному концу которой прикреплен груз 4 массы m, а к другому приложена постоянная сила F. Масса каждого блока равна m₀ и распределена по ободу равномерно. Считая, что груз 4 движется по горизонтальной плоскости с коэффициентом трения f и движение начинается из состояния покоя, определить скорость груза в зависимости от пройденного им пути и его ускорение.

Рис.13

Задача 33. Блоки радиусами r₁ и r₂ (рис.14) жестко скреплены между собой и насажены на общую ось. Грузы 1 и 2 массами m₁ и m₂, разматывая нити, намотанные на блоки, приводят их во вращение. При вращении на блоки действует момент сил сопротивления , где a – постоянная, а – угол поворота. Пренебрегая массой нитей и считая блоки однородными дисками массами М₁ и М₂ соответственно, определить угловую скорость и угловое ускорение блоков как функции угла поворота , если движение начинается из состояния покоя.

Рис.14

Задача 34. Блоки радиусами r₁ и r₂ (рис.15) жестко скреплены между собой и насажены на общую ось. Груз 2 массы m₂, разматывая намотанную на блок нить, приводит блоки во вращение и поднимает груз 1 массы m₁. При вращении на блоки действует момент сил сопротивления , где a – постоянная, а – угол поворота. Пренебрегая массой нитей и считая блоки однородными дисками массами М₁ и М₂ соответственно, определить угловую скорость и угловое ускорение блоков как функции угла поворота , если движение начнется из состояния покоя.

Рис.15

Задача 35. Грузы 1 и 2 массами m₁ и m₂ (рис.16) соединены невесомой нерастяжимой нитью, переброшенной через блок 3 радиуса r и массы m. Груз 1, опускаясь вниз по гладкой наклонной плоскости, поднимает груз 2 вверх. Считая блок однородным диском и полагая, что при вращении блока возникает постоянный момент сил сопротивления М, определить скорость груза 2 в зависимости от пройденного им расстояния и его ускорение, если угол наклона плоскости к горизонту . Движение начинается из состояния покоя.

Рис.16

Задача 36. Груз 1 (рис.17), опускаясь по вертикали, посредством невесомой и нерастяжимой нити, переброшенной через блок 3 массы m₃, заставляет катиться без скольжения однородный цилиндрический каток 2, на который намотан второй конец нити. Масса груза m₁, масса катка m₂, коэффициент трения качения k, радиусы катка и блока r. Определить скорость груза 1 в зависимости от пройденного им расстояния и его ускорение, если участок нити АВ горизонтален, а движение начинается из состояния покоя.

Рис.17

Задача 37. На неподвижную горизонтальную ось О₁ (рис.18) насажено зубчатое колесо 1 радиуса r₁ и массы m₁, а на параллельную ей ось О₂ насажены жестко скрепленные между собой зубчатое колесо 2 таких же радиуса и массы и вал 3 радиуса r₂ и массы m₂. На вал намотана невесомая веревка, к концу которой прикреплен груз 4 массы m. Считая колеса 1 и 2 однородными дисками, а вал однородным цилиндром, определить скорость и ускорение груза 4, если он опустился вниз на расстояние h без начальной скорости.

Рис.18

Задача 38. На неподвижную горизонтальную ось О₁ (рис.19) насажено зубчатое колесо 1 радиуса r₁ и массы m₁, а на параллельную ей ось О₂ насажены жестко скрепленные между собой зубчатое колесо 2 радиуса r₂ и массы m₂ и гладкое колесо 3 радиуса r₃ и массы m₃. На колесо 3 намотана невесомая веревка, к концу которой прикреплен груз 4 массы m. Считая все колеса однородными дисками, определить скорость и ускорение груза 4, если он опустился вниз на расстояние h без начальной скорости.

Рис.19

Задача 39. К кривошипу ОА эпициклического механизма (рис.20), расположенного в горизонтальной плоскости, приложен вращающий момент М₀. На оси сателлита (подвижной шестерни 1) действует постоянный момент М₁ сил сопротивления. Считая кривошип тонким однородным стержнем массы m₀, а сателлит – однородным диском массы m₁ и радиуса r₁, определить угловую скорость кривошипа как функцию угла поворота и его угловое ускорение, если в начальный момент система находилась в покое, а радиус неподвижной шестерни 2 равен r₂.

Рис.20

Задача 40. Каток 1 (рис.21), который катится без скольжения вниз по наклонной плоскости с углом наклона к горизонту, с помощью невесомой и нерастяжимой нити поднимает из состояния покоя груз 2 массы m₁ вверх по наклонной плоскости с углом . Нить перекинута через блок 3. Считая каток 1 и блок 3 однородными дисками массы m и радиусом r каждый, определить скорость тела 2 в зависимости от пройденного им пути и его ускорение. Коэффициент трения скольжения f, трением качения пренебречь.

Рис.21

Задача 41. Грузы 1 и 2 (рис.22) массами m₁ и m₂ соединены невесомой нерастяжимой нитью, переброшенной через блок 3 радиуса r и массы m. Груз 2, опускаясь, поднимает груз 1 вверх по шероховатой наклонной плоскости. Считая блок однородным диском, определить скорость груза 2 в зависимости от пройденного им расстояния и его ускорение, если коэффициент трения скольжения f, а угол наклона плоскости к горизонту . Движение начинается из состояния покоя.

Рис.22

Задача 42. Груз 1 массы m₁ (рис.23), опускаясь вертикально вниз, раскручивает ступенчатый блок 2 посредством невесомой и нерастяжимой нити, которая намотана на колесо блока радиуса r₁. На большее колесо блока, имеющее радиус r₂, намотана другая нить, второй конец которой привязан к грузу 3 массы m, скользящему по наклонной плоскости с коэффициентом трения скольжения, равным f, и углом наклона . Блок состоит из однородных дисков массами и соответственно, жестко соединенных друг с другом и имеющих общую ось вращения. Определить скорость груза 3 в зависимости от пройденного им расстояния и его ускорение, если движение начинается из состояния покоя.

Рис.23

Задача 43. Груз 1 (рис.24) массы m₁, спускаясь по наклонной плоскости с углом наклона к горизонту, с помощью невесомой и нерастяжимой нити поднимает из состояния покоя каток 2, который катится без скольжения по наклонной плоскости с углом . Нить перекинута через блок 3. Считая каток 2 и блок 3 однородными дисками массы m и радиуса r каждый, определить скорость тела 1 в зависимости от пройденного им пути и его ускорение. Коэффициент трения скольжения f, трением качения пренебречь.

Рис.24

Задача 44. Нить (рис.25), один конец которой закреплен неподвижно, огибает подвижный блок 1 (масса m, радиус r, момент инерции относительно центра масс J) и неподвижный блок 2 с тем же радиусом и моментом инерции J₁. На другом конце нити подвешен груз 3 массы m₀. Считая свободные участки нити вертикальными, определить скорость и ускорение груза 3, если он опустился вниз на расстояние h без начальной скорости.

Рис.25

Задача 45. Груз 1 (рис.26) массы m движется по горизонтальной плоскости под действием постоянной силы F, направленной под углом к горизонту, и при помощи нити вращает ступенчатый блок 2, представляющий собой два однородных диска, жестко соединенных друг с другом и имеющих общую ось вращения. На больший диск, имеющий радиус r₁ и массу m₁, намотана нить от груза 1, а на меньший, имеющий радиус r₂ и массу m₂, намотана другая нить, ко второму концу которой прикреплен груз 3 массы m₃. Определить скорость груза 1 в зависимости от пройденного им расстояния и его ускорение, если коэффициент трения скольжения равен f, участок нити АВ горизонтален, а движение начинается из состояния покоя.

Рис.26

Задача 46. Кривошип ВА гипоциклического механизма (рис.27), расположенного в горизонтальной плоскости, вращается из состояния покоя под действием постоянного момента М и приводит в движение сателлит (подвижную шестерню 1). Считая кривошип тонким однородным стержнем массы m₀, а сателлит – однородным диском массы m₁ и радиуса r₁, определить угловую скорость кривошипа как функцию угла поворота и его угловое ускорение. Радиус неподвижной шестерни 2 равен r₂.

Рис.27

Задача 47. К кривошипу ОА эпициклического механизма (рис.28), расположенного в горизонтальной плоскости, приложен вращающий момент , где М₀ и α – положительные постоянные, а – угловая скорость кривошипа. Считая кривошип тонким однородным стержнем массы m₀, а сателлит (подвижную шестерню 1) – однородным диском массы m₁ и радиуса r₁, определить угловую скорость кривошипа как функцию угла поворота и его угловое ускорение, если в начальный момент система находилась в покое, а радиус неподвижной шестерни 2 равен r₂.

Рис.28

Задача 48. Груз 1 (рис.29) массы m₁, опускаясь по вертикали, раскручивает ступенчатый блок 2 посредством невесомой и нерастяжимой нити, которая намотана на колесо блока радиуса r₁. На меньшее колесо блока, имеющее радиус r₂, намотана другая нить, второй конец которой привязан к грузу 3 массы m₃, скользящему по горизонтальной плоскости с коэффициентом трения скольжения, равным f. Блок состоит из однородных дисков массами и соответственно, жестко соединенных друг с другом и имеющих общую ось вращения. При вращении блока на него действует постоянный момент сил сопротивления М. Определить скорость груза 3 в зависимости от пройденного им расстояния и его ускорение, если движение начинается из состояния покоя.

Рис.29

Задача 49. К барабану 1 (рис.30) ворота радиуса r₁ и массы m₁ приложен вращающий момент , где a – постоянная, – угол поворота. При вращении барабана по наклонной плоскости с углом при помощи намотанного на барабан невесомого троса из состояния покоя поднимается груз 2 массы m. Считая, что коэффициент трения скольжения равен f, определить угловую скорость вращения барабана и ускорение груза 2 в зависимости от угла .

Рис.30

Задача 50. Материальная точка М, массой m, подвешенная на нити ОМ=0,4 м отведена на угол α=90° от положения равновесия и отпущена без начальной скорости (рис.31). Определить скорость этой точки во время ее прохождения через положения равновесия.

Рис.31

Задача 51. Однородный стержень массой 3 кг и длиной АВ=1 м, вращается вокруг оси ОZ по закону φ=2t³. Определить кинетическую энергию стержня в момент t=1 с.

Рис.32

Задача 52. Движущаяся механическая система состоит из четырех тел (рис.33). Центр масс тела 1 имеет скорость V. Известны радиусы R₂, R₃ тел 2 и 3. Определить кинетическую энергию тела 4 массой m₄ в зависимости от скорости V и геометрических параметров этой системы.

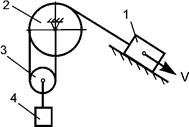
Рис.33

Задача 53. Движущаяся механическая система состоит из трех тел (рис.34). Центр масс тела 1 имеет скорость V. Известны радиусы r₃, R₃ тела 3 и его момент инерции I_c3x3 относительно оси, проходящей через центр масс. Определить кинетическую энергию тела 3 в зависимости от скорости V и геометрических параметров этой системы.

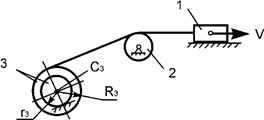
Рис.34

Задача 54. Движущаяся механическая система состоит из четырех тел (рис.35). Центр масс тела 1 имеет скорость V. Определить кинетическую энергию тела 4 массой m₄ в зависимости от скорости V и геометрических параметров этой системы.

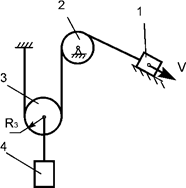
Рис.35

Задача 55. Движущаяся механическая система состоит из пяти тел (рис.36). Геометрические параметры тел известны. R₃, r₃, R₅ – соответствующие радиусы тел 3, 5. Центр масс тела 1 имеет скорость V. J_c5x5 – момент инерции тела 5 относительно оси, проходящей через его центр масс. Определить кинетическую энергию тела 5 массой m₅ в зависимости от скорости V и геометрических параметров этой системы.

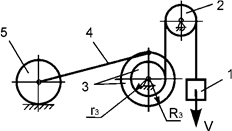
Рис.36

Задача 56. Движущаяся механическая система состоит из шести тел (рис.37). Геометрические параметры тел известны. R₂, r₂, R₃ – соответственно радиусы тел 2 и 3. J_c3x3 – момент инерции тела 3 относительно оси, проходящей через его центр масс. Центр масс тела 1 имеет скорость V. Определить кинетическую энергию тела 3 в зависимости от скорости V и геометрических параметров механизма.

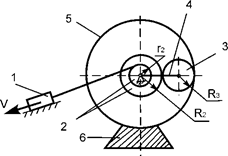
Рис.37

Задача 57. Движущаяся механическая система состоит из пяти тел (рис.38). Геометрические параметры тел известны. R₅ – радиус тела 5. Центр масс тела 1 имеет скорость V. J_c5x5 – момент инерции тела 5 относительно оси, проходящей через его центр масс. Определить кинетическую энергию тела 5 массой m₅ в зависимости от скорости V и геометрических параметров этой системы.

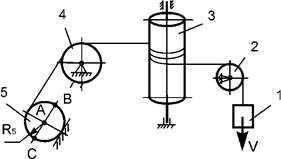
Рис.38

Задача 58. Движущаяся механическая система состоит из трех тел (рис.39). Геометрические параметры тел известны. R₂, r₂, R₃ – соответственно радиусы тел 3, 4. J_c3x3 – момент инерции тела 3 относительно оси, проходящей через его центр масс. Центр масс тела 1 имеет скорость V. Определить кинетическую энергию тела 3 в зависимости от скорости V и геометрических параметров этой системы.

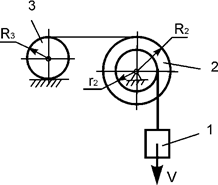
Рис.39

Задача 59. Движущаяся механическая система состоит из трех тел (рис.40). Геометрические параметры тел известны. R₂, R₃ – соответственно радиусы тел 3, 4. J_c3x3 – момент инерции тела 3 относительно оси, проходящей через его центр масс. Центр масс тела 1 имеет скорость V. Определить кинетическую энергию тела 3 в зависимости от скорости V и геометрических параметров этой системы.

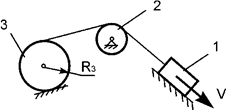
Рис.40

Задача 60. Движущаяся механическая система состоит из трех тел (рис.41). Геометрические параметры тел известны. R₃, r₃ – соответственно радиусы тела 3. J_c3x3 – момент инерции тела 3 относительно оси, проходящей через его центр масс. Центр масс тела 1 имеет скорость V. Определить кинетическую энергию тела 3 в зависимости от скорости V и геометрических параметров этой системы.

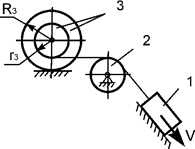
Рис.41

Задача 61. Движущаяся механическая система состоит из четырех тел (рис.42). Геометрические параметры тел известны. R₃ – радиус тела 3. Центр масс тела 1 имеет скорость V. Определить кинетическую энергию тела 4 массой m₄ в зависимости от скорости V и геометрических параметров этой системы.

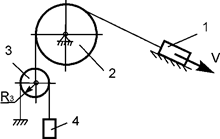
Рис.42

Задача 62. Движущаяся механическая система состоит из трех тел (рис.43). Геометрические параметры тел известны. R₃, r₃ – радиусы тела 3. J_c3x3 – момент инерции тела 3 относительно оси, проходящей через его центр масс. Центр масс тела 1 имеет скорость V. Определить кинетическую энергию тела 3 в зависимости от скорости V и геометрических параметров этой системы.

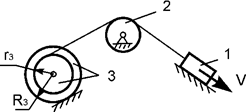
Рис.43

Задача 63. Движущаяся механическая система состоит из четырех тел (рис.44). Геометрические параметры тел известны. Центр масс тела 1 имеет скорость V. Определить кинетическую энергию тела 4 массой m₄ в зависимости от скорости V и геометрических параметров механизма.

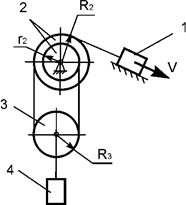
Рис.44

Задача 64. Движущаяся механическая система состоит из четырех тел (рис.45). Геометрические параметры тел известны. J_c4x4 – момент инерции тела 4 относительно оси, проходящей через его центр масс. Центр масс тела 1 имеет скорость V. Определить кинетическую энергию тела 4 массой m₄ в зависимости от скорости V и геометрических параметров механизма.

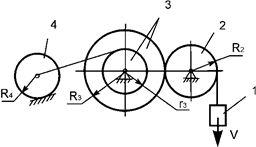
Рис.45

Задача 65. Тележка состоит из платформы 1 и колес 2 (рис.46). Платформа осуществляет поступательное движение со скоростью V. R₂ – радиус колеса 2. J_c2x2 – момент инерции колеса 2 относительно оси, проходящей через его центр масс. Определить кинетическую энергию колеса 2 массой m₂ в зависимости от скорости V и геометрических параметров платформы.

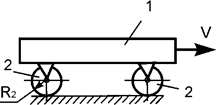
Рис.46

Задача 66. Движущаяся механическая система состоит из четырех тел (рис.47). Геометрические параметры тел известны. Центр масс тела 1 имеет скорость V. J_c4x4 – момент инерции тела 4 относительно оси, проходящей через его центр масс. Определить кинетическую энергию тела 4 в зависимости от скорости V и геометрических параметров механизма.

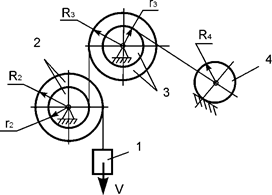
Рис.47

Задача 67. Движущаяся механическая система состоит из шести тел (рис.48). Геометрические параметры тел известны. J_c5x5 – момент инерции тела 5 относительно оси, проходящей через его центр масс. Центр масс тела 6 имеет скорость V. Определить кинетическую энергию тела 5 массой m₅ в зависимости от скорости V и геометрических параметров механизма.

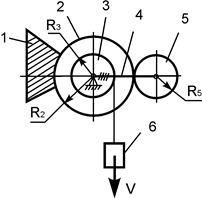
Рис.48

Задача 68. Движущаяся механическая система состоит из четырех тел (рис.49). Геометрические параметры тел известны. l₃ – длина стержня 3. Центр масс тела 1 имеет скорость V. J_c3x3 – момент инерции тела 3 относительно оси, проходящей через его центр масс. Определить кинетическую энергию тела 3 массой m₃ в зависимости от скорости V и геометрических параметров механизма.

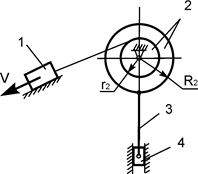
Рис.49

Задача 69. На рисунке изображен плоский механизм, состоящий из шести звеньев (рис.50). Известны геометрические параметры звеньев этого механизма. J_c4x4 – момент инерции тела 4 относительно оси, проходящей через его центр масс. Ведущее звено 6 имеет скорость V. Определить кинетическую энергию звена 4 массой m₄ в зависимости от скорости V и геометрических параметров механизма.

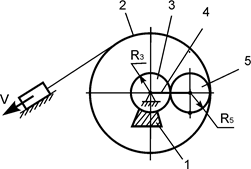
Рис.50

Задача 70. На рисунке изображен плоский механизм, состоящий из четырех звеньев (рис.51). Известны геометрические параметры звеньев этого механизма. Ведущее звено 1 имеет скорость V. Определить кинетическую энергию звена 4 массой m₄ в зависимости от скорости V и геометрических параметров механизма.

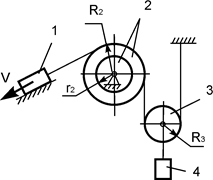
Рис.51

Задача 71. На рисунке изображен плоский механизм, состоящий из шести звеньев (рис.52). Известны геометрические параметры звеньев этого механизма. Ведущее звено 1 совершает поступательное движение со скоростью V. J_c6x6 – момент инерции тела 6 относительно оси, проходящей через его центр масс. Определить кинетическую энергию звена 6 массой m₆ в зависимости от скорости V и геометрических параметров этого механизма.

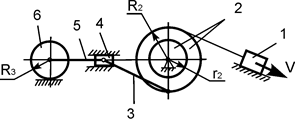
Рис.52

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00