Главная
Лекция 7 (Продолжение). Задачи для самостоятельного решения.
Задача 1. В системе тел, изображенной на рис.1, массы тел равны
m0, m1, m2, массы
блоков и нитей пренебрежимо малы. Найти ускорение тела m1.
Рис.1
Задача
2. К вращающемуся
горизонтальному диску на расстоянии d от оси вращения привязана нить длиной l с грузиком на конце (рис.2). Нить с вертикалью составляет угол α. На каком расстоянии от оси вращения диска может удержаться небольшое
тело, положенное на него, если коэффициент трения равен μ.
Рис.2
Задача
3. На валик радиусом r насажен сплошной диск. К валику
прикреплены нити одинаковой длины, при помощи которых прибор подвешивается к
штативу (рис.3). Путем симметричного наматывания нитей диск поднимают, а затем
предоставляют системе свободно опускаться. Суммарная масса валика и диска равна
m1, а
момент инерции этой системы равен J.
Сквозь отверстие в валике свободно (без трения) проходит тонкий стержень, к
которому подвешено тело массой m2. Определить ускорение, с которым опускается диск.
Рис.3
Задача 4. Однородный стержень ОА длиной l и массой m вращается
относительно оси OZ с постоянной угловой скоростью
ω (рис.4). Используя принцип Даламбера, записать уравнения динамического
равновесия.
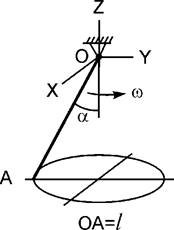
Рис.4
Задача 5. Механическая система, состоящая из трех тел массами m1, m2, m3,
вращается относительно вертикальной оси с постоянной угловой скоростью ω (рис.5).
Шарик 3 принять за материальную точку. Тела 1, 2 - однородные стержни. l – длина
стержня 1. Используя принцип Даламбера, составить уравнения динамического
равновесия механической системы.
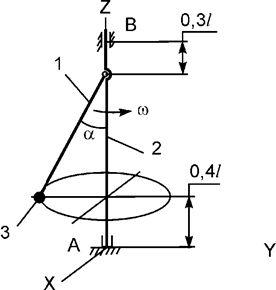
Рис.5
Задача 6. Механическая система, состоящая из трех тел массами m1, m2, m3,
вращается относительно вертикальной оси с постоянной угловой скоростью ω (рис.6). Тела 1, 2, 3 – однородные стержни. l1 = l3 = l – длины стержней
1, 3. Используя принцип Даламбера, составить уравнения динамического равновесия
механической системы.
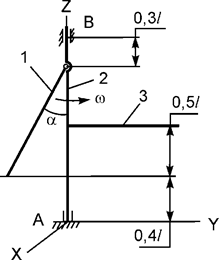
Рис.6
Задача 7. Механическая система, состоящая из трех тел массами m1, m2, m3,
вращается относительно горизонтальной оси с постоянной угловой скоростью ω
(рис.7). Тела 1, 2, 3 –
однородные стержни. Используя принцип Даламбера, составить уравнения
динамического равновесия механической системы.
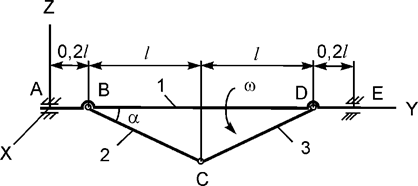
Рис.7
Задача 8. Механическая система, состоящая из двух однородных
стержней 1, 2 массами m1, m2 и
невесомой нити 3, вращается относительно горизонтальной оси с постоянной
угловой скоростью ω (рис.8). Используя принцип Даламбера, составить
уравнения динамического равновесия механической системы.
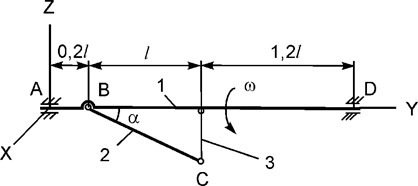
Рис.8
Задача 9. Механическая система, состоящая из двух однородных стержней
1, 2 массами m1, m2 и невесомой нити 3, вращается относительно
горизонтальной оси с постоянной угловой скоростью ω (рис.9). Используя принцип Даламбера, составить
уравнения динамического равновесия механической системы.
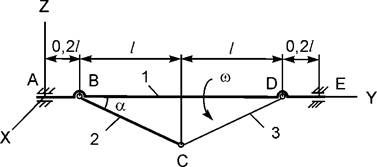
Рис.9
Задача 10. Механическая система, состоящая из двух однородных
стержней 1, 2 массами m1, m2 и невесомой нити 3, вращается относительно
горизонтальной оси с постоянной угловой скоростью ω (рис.10). Используя принцип Даламбера, составить
уравнения динамического равновесия механической системы.
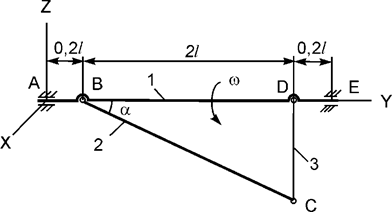
Рис.10
Задача 11. Механическая система, состоящая из двух однородных
стержней 1, 2 массами m1, m2 и невесомой нити 3, вращается относительно
горизонтальной оси с постоянной угловой скоростью ω (рис.11). Используя
принцип Даламбера, составить уравнения динамического равновесия механической
системы.
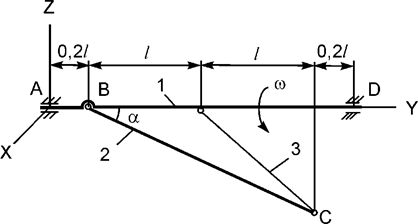
Рис.11
Задача 12. Механическая система, состоящая из двух грузов 1, 2
массами m1, m2,
однородного диска 3 массой m3, невесомых стержней 4, 5 и нити, приходит в движение из
состояния покоя (рис.12). М – активный момент; R3 – радиус
тела 3; Jc3x3 – момент инерции тела 3 относительно оси, проходящей
через его центр масс. Используя принцип Даламбера, составить уравнения
динамического равновесия механической системы.
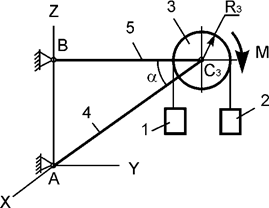
Рис.12
Задача 13. Механическая система, состоящая из груза 1 массой m1,
однородного диска 2 массой m2, невесомых стержней 3, 4 и нити, приходит в движение
из состояния покоя (рис.13). Р – активная сила; М –
активный момент; R2 – радиус тела 2; Jc2x2 – момент инерции тела 2 относительно оси, проходящей
через его центр масс. Используя принцип Даламбера, составить уравнения
динамического равновесия механической системы.
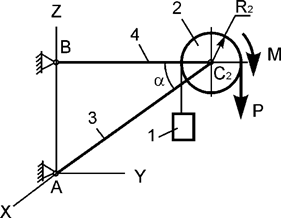
Рис.13
Задача 14. Механическая система, состоящая из балки 1 массой m1,
однородного диска 2 массой m2, груза 3 массой m3 и нити,
приходит в движение из состояния покоя (рис.14). Jc2x2 – момент
инерции тела 2 относительно оси, проходящей через его центр масс. Используя принцип Даламбера, составить уравнения
динамического равновесия механической системы.
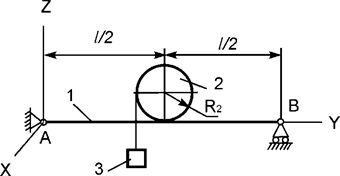
Рис.14
Задача 15. Механическая система, состоящая из балки 1 массой m1,
однородного диска 2 массой m2, груза 3 массой m3 и нити,
приходит в движение из состояния покоя (рис.15). Р –
активная сила; М2 – активный момент; R2 – радиус
тела 2; Jc2x2 – момент инерции тела 2 относительно оси, проходящей
через его центр масс. Используя принцип Даламбера, составить уравнения
динамического равновесия механической системы.
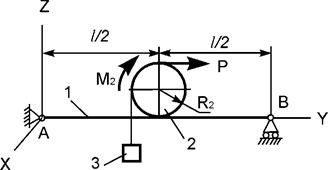
Рис.15
Задача 16. Механическая система, состоящая из однородного диска 1
массой m1, груза 2
массой m2,
невесомых стержней 3, 4 и нити, приходит в движение из состояния покоя
(рис.16). Р – активная сила; М1 – активный
момент; R1 – радиус
тела 1; Jc1x1 – момент инерции тела 1 относительно оси, проходящей
через его центр масс. Используя принцип Даламбера, составить уравнения
динамического равновесия механической системы.
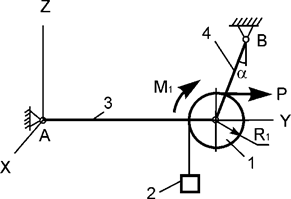
Рис.16
Задача 17. Механическая система, состоящая из ступенчатого диска
1 массой m1, груза 2 массой m2,
невесомых стержней 3, 4 и нити, приходит в движение из состояния покоя
(рис.17). Р – активная сила; R1, r1 –
радиусы тела 1; Jc1x1 – момент инерции тела 1 относительно оси, проходящей
через его центр масс. Используя принцип Даламбера, составить уравнения
динамического равновесия механической системы.
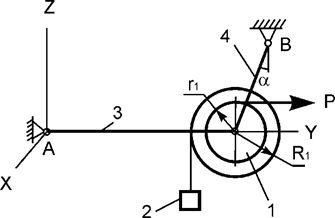
Рис.17
Задача 18. Механическая система, состоящая из ступенчатого диска
1 массой m1, груза 2 массой m2,
невесомых стержней 3, 4 и нити, приходит в движение из состояния покоя
(рис.18). Р – активная сила; R1, r1 –
радиусы тела 1; Jc1x1 – момент инерции тела 1 относительно оси, проходящей
через его центр масс. Используя принцип Даламбера, составить уравнения
динамического равновесия механической системы.
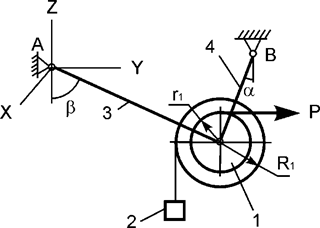
Рис.18
Задача 19. Механическая система, состоящая из ступенчатого диска
1 массой m1, груза 2 массой m2,
невесомого стержня 3 и нити, приходит в движение из состояния покоя (рис.19). Р – активная сила; R1, r1 – радиусы тела 1; Jc1x1 – момент инерции тела 1 относительно оси, проходящей
через его центр масс. Используя принцип Даламбера, составить уравнения
динамического равновесия механической системы.
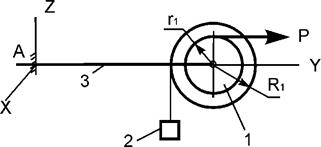
Рис.19
Задача 20. Механическая система, состоящая из ступенчатого диска
1 массой m1, грузов 2, 3 массами m2, m3, невесомого
стержня 4 и нити, приходит в движение из состояния покоя (рис.20). М1 – активный момент; R1, r1 –
радиусы тела 1; Jc1x1 – момент инерции тела 1 относительно оси, проходящей
через его центр масс. Используя принцип Даламбера, составить уравнения динамического
равновесия механической системы.
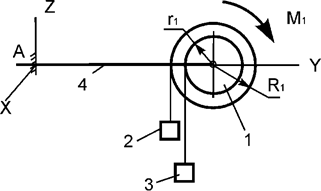
Рис.20
Задача 21. Механическая система, состоящая из ступенчатого диска
1 массой m1, грузов 2, 3 массами m2, m3, невесомого
стержня 4 и нити, приходит в движение из состояния покоя (рис.21). М1 – активный момент; R1, r1 –
радиусы тела 1; Jc1x1 – момент инерции тела 1 относительно оси, проходящей
через его центр масс. Используя принцип Даламбера, составить уравнения динамического
равновесия механической системы.
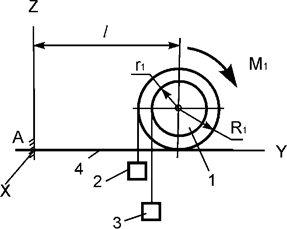
Рис.21
Задача 22. Механическая система, состоящая из ступенчатого диска
1 массой m1, грузов 2, 3 массами m2, m3,
невесомого стержня 4 и нити, приходит в движение из состояния покоя (рис.22). Р – активная сила; R1, r1 – радиусы тела 1; Jc1x1 – момент инерции тела 1 относительно оси, проходящей
через его центр масс. Используя принцип Даламбера, составить уравнения
динамического равновесия механической системы.
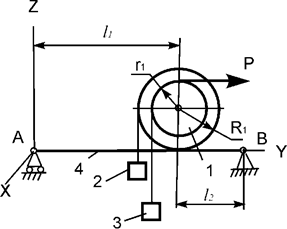
Рис.22
Задача 23. Механическая система, состоящая из ступенчатого диска
1 массой m1, грузов 2, 3 массами m2, m3, невесомых
стержней 4, 5 и нити, приходит в движение из состояния покоя (рис.23). Р – активная сила; R1, r1 – радиусы тела 1; Jc1x1 – момент инерции тела 1 относительно оси, проходящей
через его центр масс. Используя принцип Даламбера, составить уравнения динамического
равновесия механической системы.
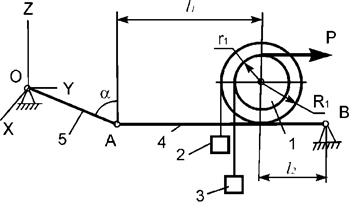
Рис.23
Задача 24. Шарик В движется в вертикальной плоскости по внутренней
поверхности цилиндра радиуса R = 0,5 м (рис.24).
Определить минимальную скорость шарика, при которой в указанном положении не
произойдет его отрыва от цилиндра.
Рис.24
Задача 25. Шарик В, находящийся на вершине гладкого
сферического купола радиуса R =
Рис.25
Задача 26. Определить,
с каким ускорением а надо перемещать клин 1 по
горизонтальной плоскости, чтобы шарик 2 не скользил по его наклонной стороне
(рис.26).
Рис.26
Задача
27. Клин 1 массой m опускается
по наклонной стороне клина 2, образующей угол α = 30° с горизонтом (рис.27). Определить давление клина 2 на
пол, если его масса равна М.
Рис.27
Задача 28. Барабан
лебедки радиусом r, установленной на балке AВ вращается с угловым ускорением ε. Масса поднимаемого груза - т, масса лебедки -
М (рис.28). Центр тяжести лебедки
находится на одинаковом расстоянии от опор А и В. Момент инерции барабана лебедки
вместе с двигателем равен J0 длина
балки - 2l. Пренебрегая массами каната и самой балки, определить
реакции опор А и В.
Рис.28
Задача 29. Барабан
лебедки радиусом r, установленной на консольной балке АВ, вращается с угловым ускорением ε (рис.29). Масса поднимаемого груза - т, масса лебедки -
М. Центр тяжести лебедки находится на
расстоянии l от вертикальной стены. Момент инерции барабана
лебедки вместе с двигателем равен J0 .
Пренебрегая массами каната и самой
балки, найти реакции заделки.
Рис.29
Задача 30. Тонкий
однородный стержень АВ массой т и длиной l вращается
с постоянной угловой скоростью ω вокруг
вертикальной оси ОО1 (ось Оу) (рис.30).
Вычислить угол отклонения стержня от вертикали, не учитывая
трение в шарнире А. При каком наименьшем значении ω стержень
отклонится от вертикали?
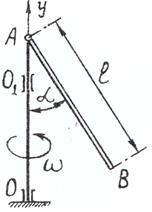
Рис.30
Задача 31. Тонкий
однородный стержень АВ массой т, расположенный в горизонтальной
плоскости, вращается с постоянной угловой скоростью ω вокруг вертикальной оси О,
с которой он скреплен одинаковыми невесомыми стержнями OA и ОВ длиной l (рис.31).
Определить реакции этих стержней.
Рис.31
Задача
32. Тонкий однородный стержень АВ массой m и длиной l вращается с постоянной угловой скоростью ω
вокруг вертикальной оси OO1 (ось Оу) (рис.32). Стержень закреплен на оси
вращения при помощи шарнира А и невесомого
стержня ВД, положение стержня АВ определяется
углами α и β. Определить реакции связей стержня АВ.
Рис.32
Задача
33. Тонкое однородное проволочное
кольцо массой m и радиусом R вращается с
постоянной угловой скоростью ω вокруг оси О, проходящей через центр О
перпендикулярно его плоскости (рис.33). Наибольшее усилие, которое выдерживает
проволока при растяжении, равно S. С какой
наибольшей скоростью ω может вращаться кольцо без разрыва. Расстояние от
центра О до центра тяжести полуокружности хс = 2R/𝜋.
Рис.33
Задача 34. Тонкий
однородный стержень OA массой
m и
длиной l, расположенный в горизонтальной плоскости, вращается
с постоянной угловой скоростью ω вокруг
вертикальной оси О (рис.34). Определить продольное
растягивающее усилие в сечении стержня в функции его координаты х.
Рис.34
Задача
35. Горизонтальные невесомые стержни
ВС и ДЕ, на концах которых закреплены точечные грузы С и Е массой m, вращаются
вокруг вертикальной оси Оу с постоянной
угловой скоростью ω (рис.35). Даны размеры: ВС=ДЕ=l и
ОД=ДВ=ВА=b. Определить реакции подпятника О
и подшипника А.
Рис.35
Задача
36. Невесомый стержень ВС
длиной l, на конце которого расположен точечный груз С массой т, вращается вокруг
вертикальной оси OA
(оси Оу)
с постоянной угловой скоростью ω (рис.36). Расстояние от шарнира В до оси вращения равно b.
Определить значение угловой скорости ω, если стержень ВС отклонился
от вертикали на угол φ.
Рис.36
Задача
37. Однородная проволочная окружность
массой m радиусом R вращается с
постоянной угловой скоростью ω вокруг оси
OA (оси
Оу)
(рис.37). Определить реакции в точках крепления В
и Д кольца к стержню OA. Расстояние от центра тяжести полукольца до оси Оу хс =2R/π.
Рис.37
Задача 38. Однородный
полукруг массой т и радиусом R вращается с
постоянной угловой скоростью со вокруг оси OA (оси Оу) (рис.38).
Определить реакции подпятника О и
подшипника А. Расстояние от центра тяжести полукруга до оси Оу хс =4R/3𝜋.
Рис.38
Задача
39. Тонкие однородные стержни ABC и
АДЕ одинаковой массы m, изогнутые под прямым углом, соединены в точке А шарниром (рис.39). Стержни вращается
вокруг вертикальной оси Оу с постоянной угловой скоростью ω. При этом они удерживаются в положении, при котором
части ВС и ДЕ параллельны, а АВ и АД перпендикулярны оси
вращения, при помощи пружины СЕ. Определить усилие в пружине.
Рис.39
Задача
40. Тонкий однородный стержень АВ
массой т и длиной 2l, закрепленный шарнирно в своей середине О на оси ОО1 (оси Оу), вращается вокруг этой оси с постоянной
угловой скоростью ω (рис.40). При этом он удерживается в положении,
образующем угол α с осью OO1 мри помощи пружины АД.
Определить усилие в пружине.
Рис.40
Задача
41. Тонкий однородный стержень АВ массой m и длиной l, закрепленный шарнирно на оси ОО1
(оси Оу), вращается вокруг этой оси с
постоянной угловой скоростью ω, образуя с
ней угол α
(рис.41). Определить усилие в пружине
ВД.
Рис.41
Задача
42. Тонкий однородный и гладкий диск
массой m и радиусом R установлен
между валом ОО1 и стержнем АВ,
приваренным к валу под углом α. Стержень
и вал вращается вместе с диском с постоянной угловой скоростью ω. Определить давление диска на стержень и вал.
Рис.42
Задача 43. Применяя принцип Даламбера, определить:
- силы реакции внешних связей – подпятника и
цилиндрического подшипника (варианты 1–24) или двух подшипников (варианты
25–30);
- внутренние усилия: в пружине (варианты 1–12), в
сечении S невесомого стержня 1 (варианты 13–24), в сечении Y вала (варианты 25–30).
Силы реакций и внутренние усилия требуется определить
в положении систем, указанных на рис. 43, т.е. в момент времени, когда все
элементы системы находятся в плоскости рисунка.
Положения сечений S
и Y заданы соответственно расстоянием
от конца стержня 1, лежащего на оси вращения, и от точки A вала. Величины этих расстояний приведены в табл. 1 в столбцах 1 и
2 соответственно. Точка A крепления
вала фиксирована, а положение другой точки крепления в подшипнике приведено в
табл. 1 в столбце 3. Точки крепления невесомого (прямолинейного или ломаного)
стержня 1 и однородного стержня 2 указаны в табл. 1 в столбцах 4 и 5
соответственно. Точки B, C,
D в табл. 1 делят вал AE на
четыре равные части AB
= BC = CD = DE = 1,5 м.
Все стержни имеют одинаковую длину L, стержень 1 невесомый, а стержни 2, 3,
4 имеют одинаковую массу 
(кг/м) единицы длины. Величины L и , а также углы 
в градусах
приведены в табл. 1. Положение стержня 4 и конца ломаного стержня 1 с точечной
массой не зависит от угла 
, а соответствует горизонтальному или вертикальному
положению, показанному на рисунках.
Масса m
точечного груза, закрепленного на стержне 1, равна 5 кг. Невесомая пружина, удерживающая стержень 3 в заданном
положении (варианты 1–12), соединена с валом и стержнем 2 идеальным
цилиндрическим подшипником. Все остальные связи также считать идеальными.
Поперечными размерами стержней и вала, а также веса вала можно пренебречь.
Закон изменения угла поворота вала 
(рад) при вращении приведен в табл. 2 для
каждого варианта, остальные углы заданы в градусах. Строка в табл. 1 определяет
подвариант и дается преподавателем.
Таблица 1
|
|
1 |
2 |
3 |
4 |
5 |
L, м |
|
|
|
|
|
1 |
0,5L |
4 |
E |
D |
B |
1,5 |
60 |
120 |
30 |
3 |
|
2 |
0,7L |
4 |
D |
E |
C |
1 |
30 |
150 |
60 |
4 |
|
3 |
0,8L |
2 |
C |
B |
D |
1,2 |
45 |
135 |
30 |
2 |
|
4 |
0,3L |
2 |
E |
D |
C |
1 |
60 |
120 |
45 |
4 |
Таблица 2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
3(t + 1) |
4(2 – t) |
5(2 + t) |
(1 + t)/3 |
(1 + 4t)/5 |
(5 – 2t)/3 |
(1 + t)/3 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
(3t + 1)/5 |
3(1 – t) |
(2 + 3t)/5 |
(1 + 4t)/8 |
(1 – 2t)/2 |
4(1 – 2t) |
5(1 + t/2) |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
5(t/2 + 2) |
2(2 – t/3) |
5(2 + t/4) |
(5 + 2t)/3 |
(4t – 2)/2 |
3(5 – t/2) |
(1 + 4t)/3 |
|
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
5(t/4 + 2) |
3(2 – t/5) |
5(2 + t/4) |
(1 + 3t)/4 |
(1 + t)/5 |
(1 – 4t)/3 |
(5 + 5t)/3 |
|
29 |
30 |
|
|
|
|
|
|
3t + 7 |
8 – t/3 |
|
|
|
|
|
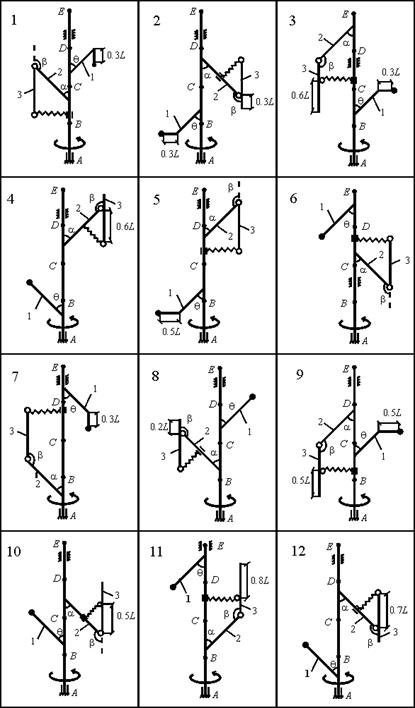
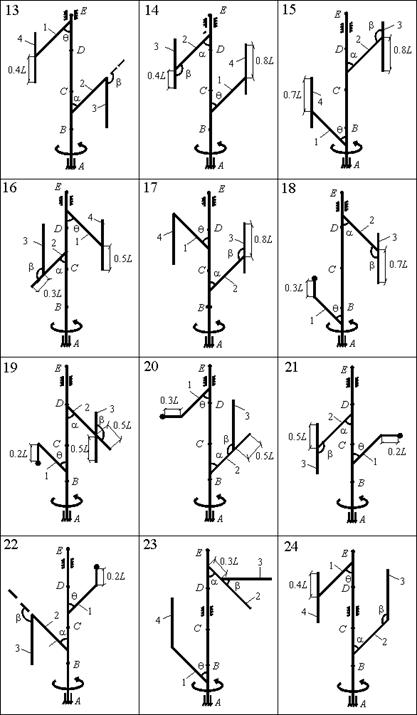
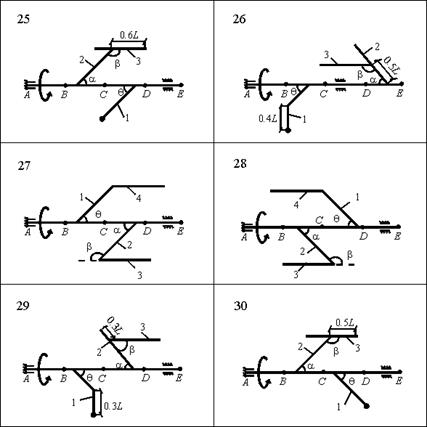
Рис. 43
Пример
решения задачи 43. Невесомый вал AE (рис. 44) длиной 6 м (AB = BC =
CD = DE = 1,5 м)
вращается по закону 
. К валу в точке E
жестко прикреплен невесомый стержень 1, а в точке D – однородный стержень 2. На конце стержня 1 закреплен точечный
груз массы m = 3 кг. К стержню 2 шарнирно
прикреплен однородный стержень 3, свободный конец которого удерживается в
заданном состоянии невесомой пружиной. Все стержни имеют одинаковую длину L = 2 м, а масса единицы
длины однородных стержней 2, 3 = 2 кг/м.
Углы 
= 30°, 
= 150°, = 60°.
В момент времени, когда все элементы системы находятся
в плоскости , определить:
- реакции связей, подпятника и подшипника в
точках A и C вала;
- усилия в пружине и в сечении S стержня 1, если расстояние ES = 0,5 L.
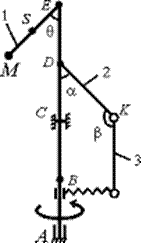
Рис.44
Решение. Для определения искомых реакций связей рассмотрим
движение заданной механической системы и применим принцип Даламбера. Введем
координаты x, y
(рис. 45) и определим величину,
направление действия и точки приложения сил, действующих на систему. Начнем с
определения сил инерции. Так как вал вращается равномерно с угловой скоростью 
рад/с, то все элементы системы,
обладающие массой, имеют только нормальные составляющие ускорения 
, где 
– кратчайшее
расстояние от j-го
элемента точечной массы 
до оси
вращения.
Рис.45
Следовательно, силы инерции 
в
рассматриваемом случае направлены от вала, перпендикулярно ему и лежат в
плоскости рисунка (рис.46). Для точечной массы, закрепленной на стержне 1,
имеем
, (1)
где радиус вращения точечной массы равен 
м.
Что касается однородных стержней 2 и 3,
то на каждый j-й элемент длины 
этих стержней
действует сила инерции 
. Эпюры параллельных сил инерции для стержня 2
образуют треугольник DGK, а для
стержня 3 – прямоугольник KFNG (см. рис. 46).
Рис.46
Каждую из полученных систем сил инерции заменим ее
равнодействующей. Так как модуль главного вектора сил инерции любого тела имеет
значение 
, где m –
масса тела, a 
– ускорение
центра масс, то для стержней 2 и 3 соответственно получим
(2)
Ускорения центров масс стержней 2 и 3 равны
(3)
где h2, h3 – расстояния
от центров масс стержней 2 и 3 до оси вращения: 
м, 
м.
Подставив в (2) формулы (3) и вычисляя полученное, находим: 
При этом линии
действия равнодействующих 
пройдут через
центры тяжестей соответствующих эпюр сил инерции. Следовательно, точка
приложения силы 
расположена на
расстоянии DL = 2 /3L от точки D, а силы 
– на расстоянии
KT = L /2 от точки K (см.
рис. 45, 46).
Определим теперь активные силы – силы тяжести
точечного груза P1 и стержней P2 и P3:
P1=mg=30 Н, P2=P3=
.
Точки приложения этих сил совпадают с центрами масс
рассматриваемых элементов системы, а направления – с направлением ускорения
свободного падения g (см. рис. 45).
Освободим механическую систему от внешних связей,
заменим действие подпятника реакциями 
, а действие подшипника – реакцией RC, которая направлена перпендикулярно к валу (см.
рис. 46).
Таким образом, определив все силы и изобразив их на отдельном
рисунке, приступим к нахождению реакций опор. Согласно принципу Даламбера,
приложенные к механизму активные силы, силы реакции и силы инерции образуют
уравновешенную систему сил (см. рис.26). Поскольку система плоская, то для
нее можно составить три уравнения равновесия
В уравнении моментов сил относительно точки A плечи сил равны:
H1 = AE – Lcos60° = 5 м,
Н2 = AD – 2Lcos30°/3 = 3,34 м,
Н3 = AD – Lcos30° = 1,77 м.
Решая систему уравнений (4), находим искомые реакции
связей:
RC = –257 Н, RAx = –206 Н, RAy = 110 Н.
Определим теперь реакцию пружины и внутренние усилия
стержня 1 в сечении S. Для нахождения
усилия пружины рассмотрим отдельно равновесие стержня 3, на который действует
реакция пружины RП.
Действие шарнира K заменим реакциями 
и 
. Изобразим стержень 3 вместе с действующими на него
силами – силой тяжести P3,
реакциями , , RП и силой инерции
на отдельном
рисунке (рис. 47).
Рис.47
Вектор силы RП
направлен вдоль пружины, которая в
силу идеальности связи с валом и отсутствия веса перпендикулярна валу (при
отклонении пружины от нормали появляется реакция RПy
вдоль вала, которая будет возвращать пружину в исходное состояние). Согласно
принципу Даламбера, система сил, действующих на стержень 3, вместе с силой инерции
Ф3 находится в равновесии. Для определения RП
достаточно составить одно уравнение
равновесия – уравнение моментов относительно точки K
.
Откуда получаем RП = –128 Н. Усилие, растягивающее пружину, равно
по величине и противоположно по направлению RП. Из
уравнения видно, что это усилие вызвано только силой инерции.
Усилия в сечении S
стержня 1 являются внутренними. Чтобы найти их, условно разрежем стержень и
рассмотрим движение части MS (рис. 48).
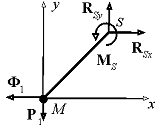
Рис.48
Действие отброшенной части стержня необходимо заменить
составляющими реакции RS=RSx+RSy и парой сил с моментом MS. Для вычисления этих
величин воспользуемся принципом Даламбера и составим для части MS три
уравнения кинетостатического равновесия
где плечи сил Р1 и Ф1 соответственно равны: h4 = Lcos30°/2 = = 0,87 м, H4 = Lsin30°/2 = 0,5 м.
В результате решения этой системы уравнений находим: MS = 140 Нм, RSx = 322,2 Н, RSy = 30 Н.
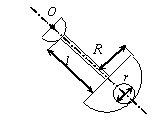
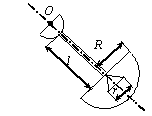
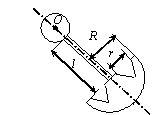
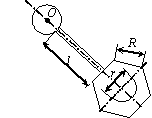
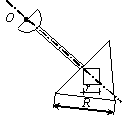
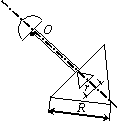
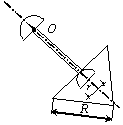
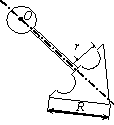
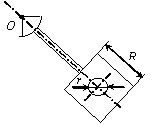
Задача 44. Физический маятник представляет собой твердое тело
(варианты 1–30 на рис.49), состоящее из круглой или полукруглой однородной
пластины диаметром d = 0.2 м,
однородного стержня длиной l = 0,8 м и пластины с вырезом. Форма
пластин с вырезом варьируется. Так, в вариантах 1–5 она имеет
форму полукруга радиусом R = 1 м, в вариантах 6–10 – это правильный
шестиугольник со стороной R = 1 м, в вариантах 11–15 и 21–25 – квадрат
со стороной R = 1 м, в вариантах 16–20 – правильный
треугольник со стороной R = 1 м, в вариантах 26–30 – сектор с
центральным углом 270о и 90о. Вырез(ы) изображены на рис.49 и имеют характерный размер r = 0,25 м. Масса погонного метра стержня 
= 10 кг/м,
масса 1 м2 пластин 
= 150 кг/м2.
Определить закон движения малых колебаний физического маятника в поле тяжести.
Начальное положение маятника и его начальная угловая скорость даны в табл. 3.
Задача 45. На твердое тело, описанное в задаче 44 (варианты 1–30
на рис. 49) и находящееся в начальный момент времени t = 0 в покое, действует в отсутствии силы тяжести в
плоскости движения маятника вращающий момент Mz = bt + c,
где постоянные b и с даются в табл. 3. Найти закон вращения данного тела и
определить для произвольного момента времени кинетическую энергию, кинетический
момент относительно оси вращения и работу, совершенную внешними силами.
Таблица 3
|
Варианты |
|
|
b |
c |
|
1, 6, 11, 16, 21, 26 |
|
0,0 |
2 |
–32 |
|
2, 7, 12, 17, 22, 27 |
|
0,2 |
–4 |
16 |
|
3, 8, 13, 18, 23, 28 |
|
0,4 |
8 |
–8 |
|
4, 9, 14, 19, 24, 29 |
|
0,5 |
–16 |
4 |
|
5, 10, 15, 20, 25, 30 |
|
0,6 |
32 |
–2 |
Вариант 1
Вариант 2
Вариант 3 Вариант 4
Вариант 5 Вариант 6 Вариант 7 Вариант 8
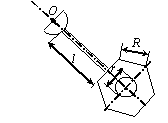
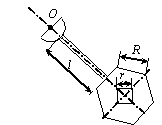
Вариант 9
Вариант 10
Вариант 11 Вариант
12
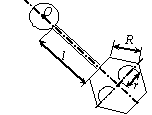
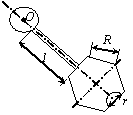
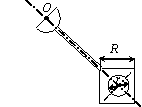
Вариант 13 Вариант 14 Вариант 15 Вариант 16
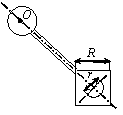
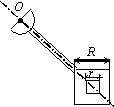
Вариант 17 Вариант 18 Вариант 19 Вариант 20
Вариант 21 Вариант 22 Вариант 23 Вариант 24
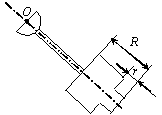
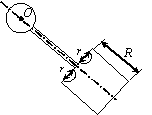
Вариант 25 Вариант 26 Вариант 27 Вариант 28
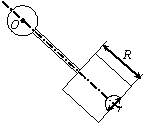
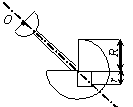
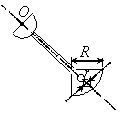
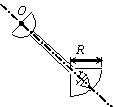
Вариант 29 Вариант 30
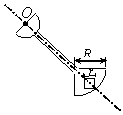
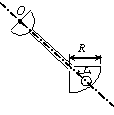
Рис.49
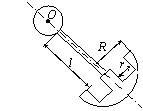
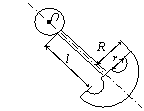
Пример
решения задачи 44. Физический маятник
(рис. 50) состоит из тонкого однородного стержня длиной l2 = 0,4 м и двух пластин, одна из которых
круглая радиуса r1 = 0,1 м,
а другая представляет собой эллипс с круглым вырезом.
Длина полуосей эллипса а3 = 0,6 м, b3 = 0,3 м,
радиус выреза r4 = 0,2 м. Центр выреза смещен в сторону
оси вращения от центра эллипса на расстояние d = 0,3 м.
Плотность стержня и пластин соответственно = 25 кг/м,
= 150 кг/м2. Ось вращения этого маятника проходит через
центр верхней круговой пластины радиуса r1
перпендикулярно плоскости тела. В начальный момент времени он отклоняется от
вертикали на угол 
и
предоставляется самому себе. Определить закон движения малых колебаний
физического маятника в поле тяжести.
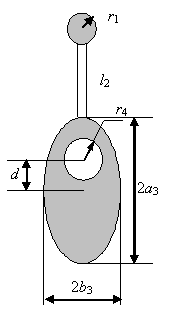
Рис.50
Решение. Уравнение вращательного движения маятника следует из
теоремы моментов относительно оси вращения Оz
. (1)
На маятник, представленный на рис. 50, действуют
две силы – сила тяжести и сила реакции шарнира в точке подвеса (рис. 51).
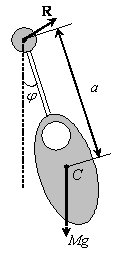
Рис.51
Поскольку момент последней силы относительно оси Оz равен нулю, то уравнение (1) для
данного физического маятника сводится к следующему
, (2)
где а –
расстояние от центра тяжести до оси вращения. Уравнение малых колебаний
физического маятника тогда принимает вид
Начальные условия для уравнения (2) имеют вид:
Теперь следует определить входящие в уравнение (2а)
положение центра тяжести а физического маятника и его момент инерции Jz. Поскольку нам необходимо знать
лишь расстояние от центра тяжести до оси вращения, то достаточно определить
координату хс
центра тяжести маятника в положении равновесия (рис. 51), которая и
равна а. Для этого разобьем тело на
следующие части: 1 – круговую пластину радиуса r1, 2 – тонкий стержень длиной l2, 3 – эллиптическую пластину без выреза, 4 – круговую
пластину (вырез) радиуса r4.
Выберем систему координат Oxy с началом на оси вращения. Тогда, воспользовавшись
методом дополнений, для искомой координаты получим выражение
где xс, xk – координаты
центров тяжести по оси Оx всего тела и k-й
его части соответственно, а Мk – масса k-й
его части. Положения центров масс частей и всего тела показаны на рис. 52.
Рис.52
Вычисляя эти величины, найдем
x1 = 0, 
кг,
x2=r1+l2/2 =0.3 м, 
кг,
x3=r1+l2+a3=1.1 м, 
кг,
x4=x3–d = 0.8 м, 
кг.
Таким образом,
Вычислим теперь момент инерции данного маятника. Для
этого снова воспользуемся введенным разбиением тела. Тогда
. (4)
Здесь Jz, Jzk – соответственно моменты инерции
всего тела и k-й его части
относительно оси вращения.
Согласно теореме Гюйгенса – Штейнера, Jzk = Jzсk + Mk xk2,
где Jzсk – моменты инерции k-й части тела относительно оси, проходящей
через центр масс этой части и параллельной оси вращения. Тогда
Откуда, используя формулу (4), находим
= 0,02 + 1,03 + 112,17
– 12,44 = 100,78 кгм2.
В результате входящая в уравнение (2а) частота
колебаний k равна
Общее решение уравнения (2а) имеет вид: 
. Закон же изменения угловой скорости физического
маятника тогда описывается выражением: 
. Используя начальные данные (3), окончательно находим
.
Пример решения
задачи 45. Задача 45 состоит в
определении характеристик вращательного движения твердого тела, описанного в
задаче 44 (см. рис. 50), если к нему прикладывается момент внешних сил Mz = 8t +2 (Нм), а сила тяжести
отсутствует (рис. 53). Итак, для указанного тела необходимо найти закон
движения и определить для произвольного момента времени кинетическую энергию,
кинетический момент относительно оси вращения и работу, совершенную внешними
силами. Начальное положение тела и его начальная угловая скорость заданы так
. (5)
Рис.53
Решение. Начнем с определения закона движения тела. Уравнение
движения теперь, в отличие от уравнения (2), имеет вид
или
Интегрируя последнее уравнение, находим закон
изменения угловой скорости тела
и закон его движения
Из начальных условий (5) находим, что c1 = 0, c2 = 0. Учитывая
дальше вычисленное выше значение момента инерции относительно оси z,
окончательно получаем
Момент количества движения рассматриваемого твердого
тела относительно оси вращения равен
Кинетическая энергия тела определяется соотношением
Наконец, работа, произведенная за время t внешним моментом, равна
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
