Главная
Лекция 8 (продолжение). Задачи для самостоятельного решения.
Задача 1. На плоскую механическую систему, состоящую из тел 1,
2, действуют активные нагрузки Р1, Р2,
q (рис.1).
Используя принцип возможных перемещений, определить горизонтальную составляющую
реакции внешней связи в точке А.
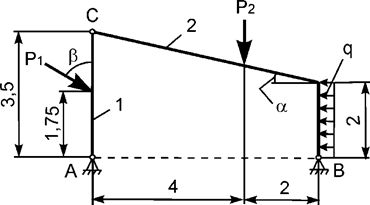
Рис.1
Задача 2. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.2). Использую принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке А.
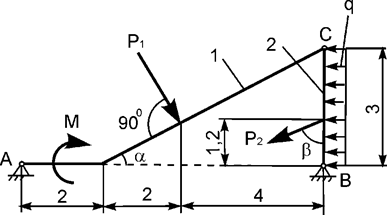
Рис.2
Задача 3. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.3). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке В.
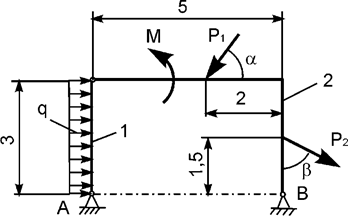
Рис.3
Задача 4. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.4). Используя принцип возможных перемещений, определить
вертикальную составляющую реакции внешней связи в точке А.
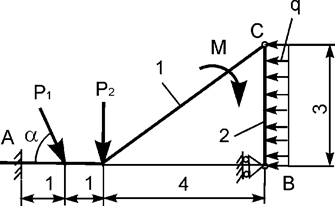
Рис.4
Задача 5. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.5). Используя принцип возможных перемещений,
определить вертикальную составляющую реакции внешней связи в точке А.
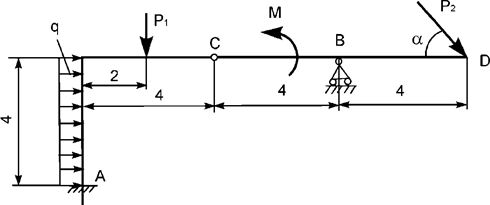
Рис.5
Задача 6. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.6). Используя принцип возможных перемещений,
определить реакцию внешней связи в точке D.
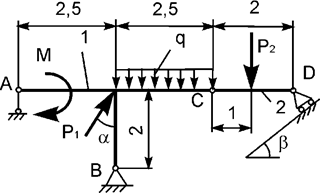
Рис.6
Задача 7. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.7). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке В.
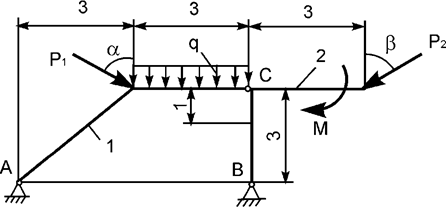
Рис.7
Задача 8. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.8). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке А.
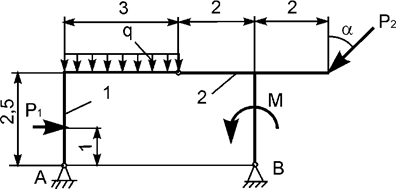
Рис.8
Задача 9. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.9). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке А.
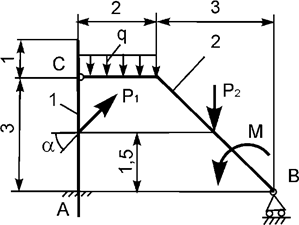
Рис.9
Задача 10. На плоскую механическую систему, состоящую из тел 1,
2, действуют активные нагрузки Р1, Р2,
q, М (рис.10). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке С.
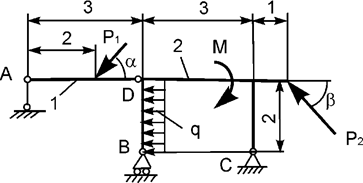
Рис.10
Задача 11. На плоскую механическую систему, состоящую из тел 1,
2, действуют активные нагрузки Р1, Р2,
q, М (рис.11). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке А.
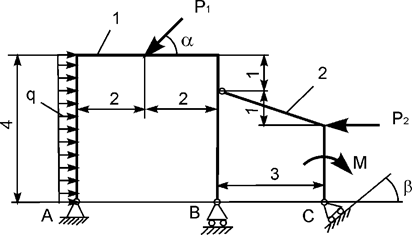
Рис.11
Задача 12. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.12). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке А.
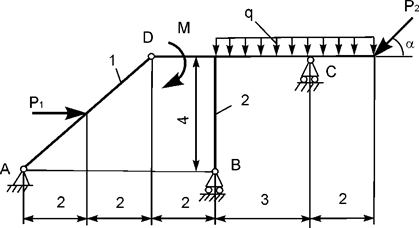
Рис.12
Задача 13. На плоскую механическую систему, состоящую из тел 1,
2, действуют активные нагрузки Р1, Р2,
q, М (рис.13). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке А.
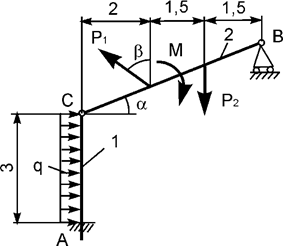
Рис.13
Задача 14. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.14). Используя принцип возможных перемещений,
определить вертикальную составляющую реакции внешней связи в точке В.
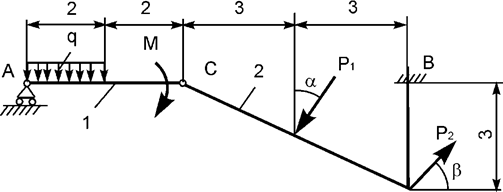
Рис.14
Задача 15. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.15). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке В.
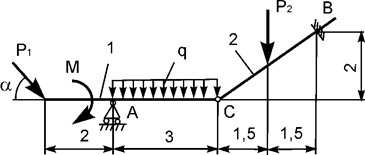
Рис.15
Задача 16. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.16). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке В.
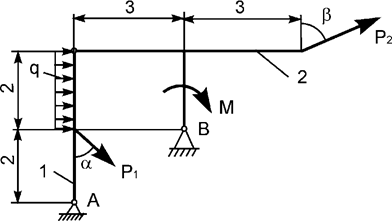
Рис.16
Задача 17. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.17). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке В.
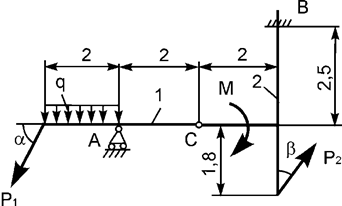
Рис.17
Задача 18. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.18). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке В.
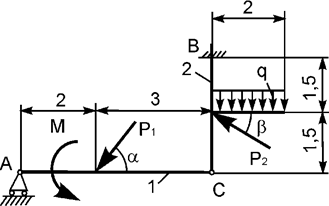
Рис.18
Задача 19. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.19). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке А.
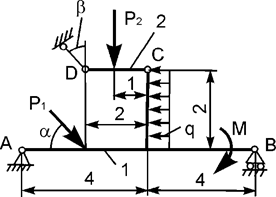
Рис.19
Задача 20. На плоскую механическую систему, состоящую из двух
тел, действуют активные нагрузки Р1, Р2,
q, М (рис.20). Используя принцип возможных перемещений,
определить горизонтальную составляющую реакции внешней связи в точке А.
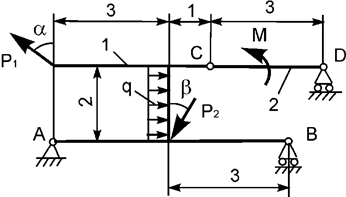
Рис.20
Задача 21. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.21).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3, m4 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила; М2
– активный момент. Составить общее уравнение динамики механической системы.
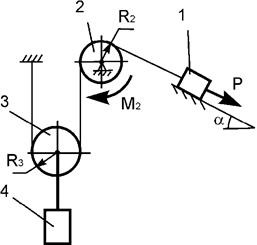
Рис.21
Задача 22. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.22).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс. Составить общее уравнение динамики
механической системы.
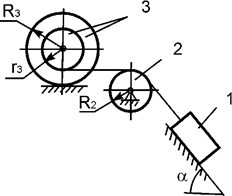
Рис.22
Задача 23. На механическую систему, состоящую из трех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.23).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила; М3
– активный момент. Составить общее уравнение динамики механической системы.
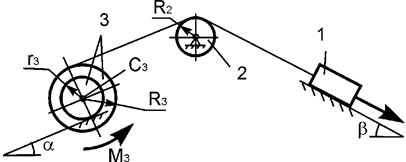
Рис.23
Задача 24. На механическую систему, состоящую из трех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.24).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила.
Составить общее уравнение динамики механической системы.
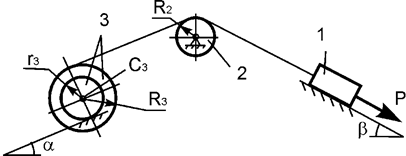
Рис.24
Задача 25. На механическую систему, состоящую из трех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.25).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс. Составить общее уравнение динамики
механической системы.
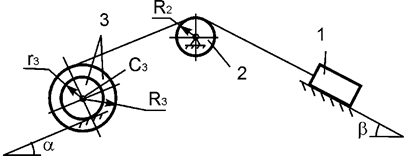
Рис.25
Задача 26. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.26).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3, m4 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила; М2
– активный момент. Составить общее уравнение динамики механической системы.
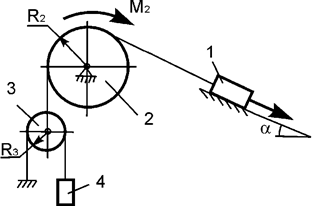
Рис.26
Задача 27. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.27).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3, m4 – массы тел; Jc2x2, Jc3x3, Jc4x4 – моменты инерции тел 2, 3, 4 относительно осей,
проходящих через их центры масс. Составить общее уравнение динамики
механической системы.
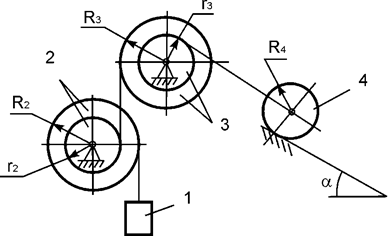
Рис.27
Задача 28. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.28).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3, m4 – массы тел; Jc2x2, Jc3x3, Jc4x4 – моменты инерции тел 2, 3, 4 относительно осей,
проходящих через их центры масс; М4 –
активный момент. Составить общее уравнение динамики механической системы.
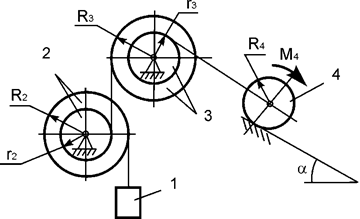
Рис.28
Задача 29. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.29).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3, m4 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила.
Составить общее уравнение динамики механической системы.
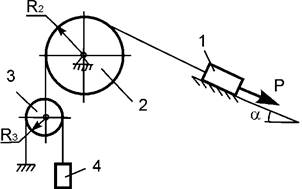
Рис.29
Задача 30. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.30).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3, m4 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс. Составить общее уравнение динамики
механической системы.
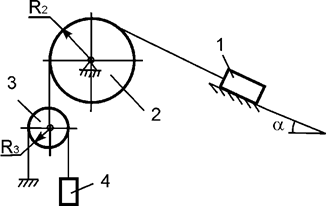
Рис.30
Задача 31. На механическую систему, состоящую из трех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.31).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила; М3
– активный момент. Составить общее уравнение динамики механической системы.
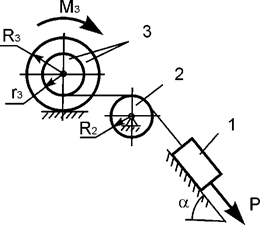
Рис.31
Задача 32. На механическую систему, состоящую из трех тел,
наложены идеальные связи. Известны
геометрические параметры системы (рис.32). Под действием активных нагрузок
механическая система движется из состояния покоя. Дано: m1, m2, m3 – массы
тел 1, 2, 3; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс. Составить общее уравнение динамики
механической системы.
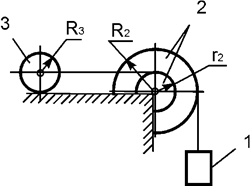
Рис.32
Задача 33. На механическую систему, состоящую из трех тел,
наложены идеальные связи. Известны
геометрические параметры системы (рис.33). Под действием активных нагрузок
механическая система движется из состояния покоя. Дано: m1, m2, m3 – массы
тел 1, 2, 3; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила.
Составить общее уравнение динамики механической системы.
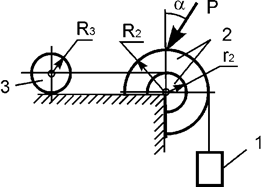
Рис.33
Задача 34. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.34).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3, m4 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс. Составить общее уравнение динамики
механической системы.
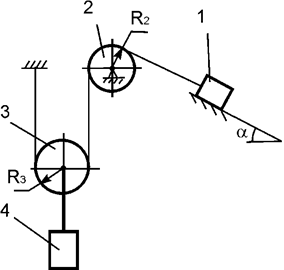
Рис.34
Задача 35. На механическую систему, состоящую из трех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.35).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила.
Составить общее уравнение динамики механической системы.
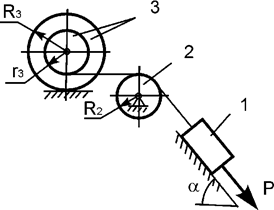
Рис.35
Задача 36. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.36).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3, m4 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила.
Составить общее уравнение динамики механической системы.
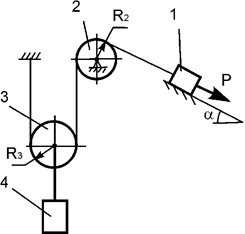
Рис.36
Задача 37. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны геометрические параметры системы (рис.37).
Под действием активных нагрузок механическая система движется из состояния
покоя. Дано: m1, m2, m3, m4 – массы тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила; М2
– активный момент. Составить общее уравнение динамики механической системы.
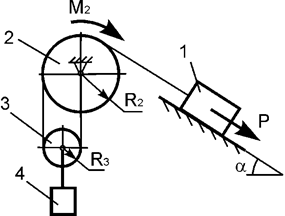
Рис.37
Задача 38. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны
геометрические параметры системы (рис.38). Под действием активных нагрузок
механическая система движется из состояния покоя. Дано: m1, m2, m3, m4 – массы
тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила.
Составить общее уравнение динамики механической системы.
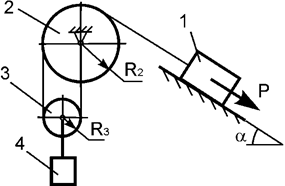
Рис.38
Задача 39. На механическую систему, состоящую из четырех тел,
наложены идеальные связи. Известны
геометрические параметры системы (рис.39). Под действием активных нагрузок
механическая система движется из состояния покоя. Дано: m1, m2, m3, m4 – массы
тел; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс. Составить общее уравнение динамики
механической системы.
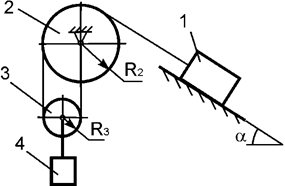
Рис.39
Задача 40. На механическую систему, состоящую из трех тел,
наложены идеальные связи. Известны
геометрические параметры системы (рис.40). Под действием активных нагрузок
механическая система движется из состояния покоя. Дано: m1, m2, m3 – массы
тел 1, 2, 3; Jc2x2, Jc3x3 – моменты инерции тел 2, 3 относительно осей,
проходящих через их центры масс; Р – активная сила; М3
– активный момент. Составить общее уравнение динамики механической системы.
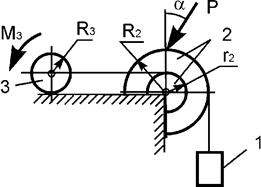
Рис.40
Задача 41. Груз
1 массой m1, опускаясь вниз по призме, приводит в движение
посредством нити, переброшенной через невесомый блок, груз 2 массой m2 (рис.41).
Определить давление призмы на вертикальный выступ пола.
Рис.41
Задача 42. Груз 1 массой m1 опускаясь
вниз, приводит в движение посредством нити, переброшенной через невесомый блок,
груз 2 массой m2 (рис.42). Определить
давление ножек стола на упор 3, скрепленный с полом.
Рис.42
Задача 43. Груз 1 массой m1 опускаясь
вниз по наклонной шероховатой плоскости с углом α, приводит во вращение при помощи нити барабан 2 массой m2 и радиусом r (рис.43).
Определить угловое ускорение барабана, считая его круглым однородным цилиндром.
Массой нити и блока пренебречь. Коэффициент трения между грузом и плоскостью
равен f.
Рис.43
Задача 44. Вал
кабестана (механизма для перемещения грузов) радиусом r приводится
в движение постоянным вращающим моментом М,
приложенным к рукоятке AВ (рис.44). Определить ускорение груза массой m, если коэффициент трения скольжения груза о
горизонтальную плоскость равен f. Момент инерции кабестана относительно оси вращения
равен Jz. Массой каната пренебречь.
Рис.44
Задача
45. Фрикционный молот состоит из двух
роликов и падающей ударной части (рис.45). Масса каждого ролика равна m. Найти
ускорение падающей ударной части, массы m1 при ее движении вверх, если к роликам приложены
равные моменты М. Ролики считать однородными дисками. Скольжение между падающей
частью и роликами отсутствует.
Рис.45
Задача 46. В
передаче вращением колесо 1 приводится в движение моментом М1
к колесу 2 приложен момент сопротивления М2 (рис.46). Найти
угловое ускорение колеса 1, считая колеса однородными дисками, массы которых m1 и m2, а радиусы — r1 и r2.
Рис.46
Задача 47. Два
шкива радиусами r1 и r2 массами m1 и m2, соединенные ремнем, вращаются вокруг параллельных
осей О1
и О2 (рис.47). Найти
угловое ускорение шкива 1, если к нему приложен вращающий момент М1, а
к шкиву 2 приложен момент сопротивления M2. Шкивы
считать однородными дисками. Скольжением ремня и его массой пренебречь.
Рис.47
Задача
48. Зная значение силы Q, определить
значение силы Р; OA = АВ =
l (рис.48).
Рис.48
Задача
49. По известному значению силы Р и моменту пары М найти значение силы Q; АВ = l (рис.49).
Рис.49
Задача
50. Зная значение момента пары М, определить значение силы Р; ОС = b,
OA =
l1, O1B = l2 (рис.50).
Рис.50
Задача
51. По известному значению силы Q
найти значение момента пары М; ОС =АС = СВ=l (рис.51).
Рис.51
Задача 52. Зная
значение момента пары М, определить
значение силы Q; ОС = l (рис.52).
Рис.52
Задача
53. По известному значению момента
пары М найти значение силы Q; радиусы
шкивов - r1, r2 и R (рис.53).
Рис.53
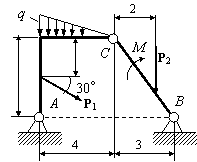
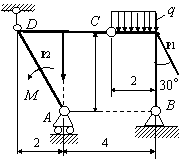
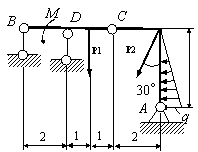
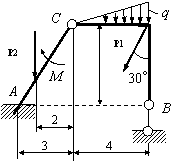
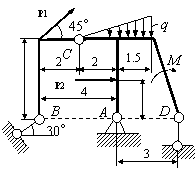
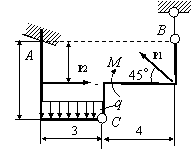
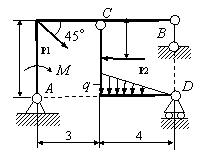
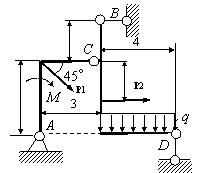
Задача 54. Применяя принцип возможных перемещений, определить
реакции связей составных конструкций. Схемы конструкций показаны на рис. 54,
а необходимые для решения данные приведены в табл. 1. На рисунках все размеры
указаны в метрах.
Таблица 1
|
Вариант |
Нагрузка |
Вариант |
Нагрузка |
||||||
|
Р1, кН |
Р2, кН |
q, кН/м |
M, кНм |
Р1, кН |
Р2, кН |
q, кН/м |
M, кНм |
||
|
1 |
15 |
14 |
3 |
10 |
16 |
3 |
10 |
2 |
10 |
|
2 |
13 |
12 |
2 |
6 |
17 |
1 |
8 |
1 |
8 |
|
3 |
11 |
10 |
1 |
5 |
18 |
3 |
6 |
3 |
6 |
|
4 |
9 |
8 |
3 |
14 |
19 |
5 |
4 |
2 |
7 |
|
5 |
7 |
6 |
2 |
12 |
20 |
7 |
2 |
1 |
5 |
|
6 |
8 |
5 |
1 |
4 |
21 |
10 |
9 |
2 |
4 |
|
7 |
7 |
4 |
2 |
10 |
22 |
8 |
7 |
1 |
7 |
|
8 |
6 |
6 |
1 |
7 |
23 |
6 |
5 |
2 |
8 |
|
9 |
5 |
8 |
3 |
8 |
24 |
4 |
3 |
1 |
3 |
|
10 |
4 |
10 |
2 |
6 |
25 |
2 |
1 |
2 |
2 |
|
11 |
12 |
11 |
1 |
12 |
26 |
7 |
1 |
2 |
7 |
|
12 |
10 |
6 |
2 |
10 |
27 |
6 |
2 |
1 |
5 |
|
13 |
9 |
5 |
1 |
6 |
28 |
5 |
3 |
2 |
10 |
|
14 |
7 |
10 |
2 |
13 |
29 |
4 |
4 |
1 |
5 |
|
15 |
6 |
8 |
1 |
5 |
30 |
3 |
5 |
2 |
10 |
Вариант 1 Вариант 2
Вариант 3 Вариант 4
Вариант 5 Вариант 6
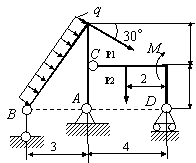
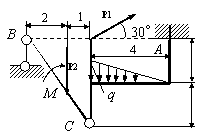
Вариант 7 Вариант 8
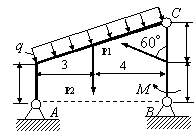
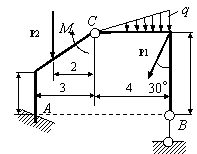
Вариант 9 Вариант 10
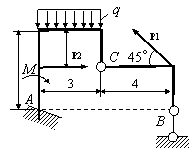
Вариант 11 Вариант 12
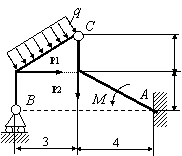
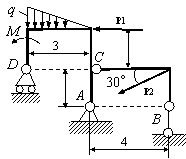
Вариант 13 Вариант 14
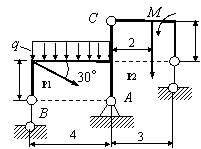
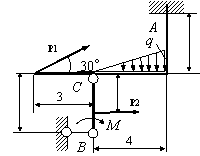
Вариант 15 Вариант 16
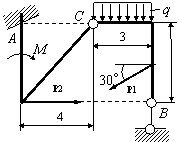
Вариант 17 Вариант 18
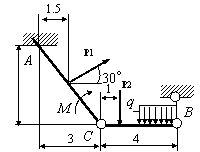
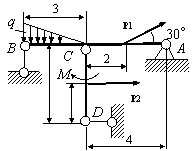
Вариант 19 Вариант 20
Вариант 21 Вариант 22
Вариант 23 Вариант 24
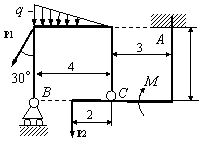
Вариант 25 Вариант 26
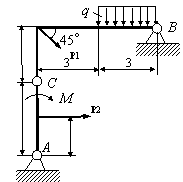
Вариант 27 Вариант 28
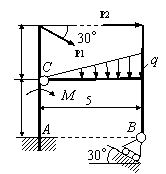
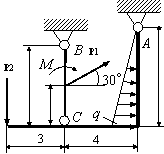
Вариант 27 Вариант 28
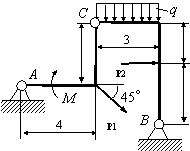
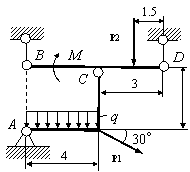
Рис. 54
Пример
решения задачи 54. Дана двухсоставная
рама, части которой соединены шарниром в точке С (рис. 55), закрепленная в
точках А и В с помощью неподвижных шарнирных опор. В точке D на раму CDB действует
сила P1=10 кН,
на раму АЕС действуют на участке ЕС распределенная по линейному закону
нагрузка с максимальной интенсивностью q = 4 кН/м и пара сил с моментом m1 = 5 кНм
(см. рис. 55). Определить горизонтальную составляющую реакции
шарнирной опоры А. Трение в шарнирах
отсутствует. Размеры элементов рам на рис. 55 даны в метрах.
Рис.55 Рис.56
Решение. Легко проверить, что в данной задаче все условия
применения принципа Лагранжа выполнены (система находится в равновесии, связи
являются стационарными, голономными, удерживающими и идеальными).
Освободимся от связи, соответствующей реакции XA
(рис. 56). Для этого в точке A неподвижный шарнир следует заменить, например,
стержневой опорой, при этом система получает одну степень свободы. Как уже
отмечалось, возможное перемещение системы определяется связями, наложенными на
нее, и не зависит от приложенных сил. Поэтому определение возможных перемещений
является кинематической задачей. Поскольку в данном примере рама может двигаться
лишь в плоскости рисунка, то и возможные ее движения являются плоскими. При
плоском же движении перемещение тела можно рассматривать как поворот вокруг
мгновенного центра скоростей. Если же мгновенный центр скоростей лежит в
бесконечности, то это соответствует случаю мгновенно поступательного движения,
когда перемещения всех точек тела одинаковы.
Для нахождения мгновенного центра скоростей необходимо
знать направления скоростей двух каких-либо точек тела. Поэтому определение
возможных перемещений составной конструкции следует начинать с нахождения
возможных перемещений того элемента, у которого такие скорости известны. В
данном случае следует начать с рамы CDB, поскольку ее точка В неподвижна и, следовательно,
возможным перемещением этой рамы является ее поворот на угол 
вокруг оси,
проходящей через шарнир B. Теперь, зная возможное перемещение 
точки С (она одновременно принадлежит обеим
рамам системы) и возможное перемещение 
точки А (возможным перемещением точки A является
ее перемещение вдоль оси х), находим
мгновенный центр скоростей C1 рамы АЕС. Таким образом, возможным
перемещением рамы АЕС является ее
поворот вокруг точки C1 на угол 
. Связь между углами и определяется
через перемещение точки C
(см. рис. 56)
Из подобия треугольников EC1C и BCD имеем
В результате получим зависимости:
Согласно принципу возможных перемещений
Последовательно вычислим входящие сюда возможные
работы:
Q=2q – равнодействующая распределенной нагрузки, точка
приложения которой показана на рис. 56; совершаемая ею возможная работа
равна:
Далее 
и
Следовательно,
Отсюда
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
