Главная
Тема 17. Количество
движения. Векторное понятие силы. Закон параллелограмма сил
С именем Декарта связало введение в динамику понятия о
количестве движения, или импульса. Рождение этого понятия появилось во Франции
в середине XIV в. в связи с начавшейся уже критикой положений схоластической
философии Аристотеля, который считал необходимым для произведения движения
наличие постоянного двигателя, находящегося в тесной связи с движимым телом.
В области астрономии эту роль выполнял так называемый
«первый двигатель», непрерывно движущий небесные сферы. Этот «первый двигатель»
схоластики отождествляли с богом.
Парижский ученый Жан Буридан считал, что для получения
движения достаточно дать телу «импульс»; при отсутствии сопротивлений движения
в надлунном мире этот мгновенно подействовавший импульс будет вечно двигать
небесные сферы. Буридан рассматривал преимущественно так называемый вращательный
импульс, но развитие военной техники конца средневековья распространило понятие
импульса и на прямолинейное движение.
В XIV в. произошло нечто аналогичное тому, что было в
IV в. до н. э., когда введение метательных машин у греков заставило
пересмотреть основные понятия динамики Аристотеля. Разница заключалась только в
том, что криволинейное движение камня, выброшенного из баллисты, заменилось
прямолинейным движением пули из мушкета или ядра из пушки.
Так как направление движения выстреленной
пули было (по крайней мере в начальный момент)
прямолинейным, то подействовавшая на нее «сила», получившая у итальянских
инженеров название impeto, кроме величины приобрела
также и направление. Ее величина считалась пропорциональной количеству вещества
(весу) тела, вылетевшего из дула орудия, и сообщенной скорости, а направление
последней определяло также и направление «силы». В результате в определение
силы вошло новое понятие, неизвестное античной механике: сила сделалась
вектором.
Так возникло понятие о количестве движения, которое
имело большое значение в философии Декарта, в частности в его исследованиях,
касающихся теории удара. После Галилея можно было считать решенным вопрос о
движении тела под действием силы тяжести. Но ведь сила тяжести не является
единственной силой, которая может приводить в движение тела; они могут
двигаться также под действием толчка или удара. Поэтому первая половина XVII в.
богата трудами, касающимися удара тел. В первую очередь следует назвать самого
Галилея, который исследование явлений удара рассматривает в сочинении «Беседы о
двух новых науках». Полученные им результаты не имеют большого значения; с
исторической точки зрения интересно лишь введение понятия о «мертвом
грузе» — статическом действии наложенного груза; примерно через семьдесят лет
оно появилось в классификации Лейбница, который делил все силы на живые и
мертвые.
Теорией удара занимался и Декарт. К этой теории
относится третий закон движения, сформулированный Декартом так: если одно тело
встречает другое и если оно имеет менее силы для продолжения движения, чем
встречаемое для сопротивления, то оно изменяет направление, не теряя ничего из
своего движения; если же оно имеет больше силы, то увлекает с собой встречаемое
тело, причем теряет из своего движения столько, сколько передает его
встречаемому телу.
Это так называемый закон сохранения количества
движения, который Декарт распространил на всю Вселенную (сумма всех количеств движения мира есть величина постоянная). Нужно отметить,
что количество движения Декарт понимал как абсолютную величину, не имеющую ни
знака, ни направления. Для удара тел, движущихся по одной прямой, Декарт дал
целый ряд правил без доказательств, как сами собой разумеющиеся.
На неудовлетворительность этих правил позднее указал
Гюйгенс. В частности, он отметил, что, исследуя явления удара двух тел,
движущихся по одной прямой, в зависимости от направления движения количеству
движения нужно придавать знак «плюс» или «минус».
Если величины (массы) сталкивающихся тел одинаковы, то
изменение их скоростей описывается как передача части скорости от одного тела к
другому. Если же массы тел не одинаковы, то изменение скоростей описывается как
передача движений «Движение» (motus) Декарта есть не
что иное, как количество движения. А если эти тела двигались бы не по одной
прямой, или одно из них — ударяемое тело — было в момент удара неподвижным?
Тогда, конечно, приобретенное движение имело направление сообщенной скорости,
т. е. было векторной величиной, направление которой характеризовалось направлением сообщенной скорости.
Если одно и то же тело, находясь в состоянии покоя, испытывало различные удары,
то отношения полученных движений могли бы характеризоваться только величинами
сообщенных скоростей.
Различные движения одного и того же тела можно было
изображать перемещениями, которые это тело получало за один и тот же
определенный промежуток времени.
Таким образом, сила удара, а затем и вообще любая
сила, могла быть охарактеризована величиной перемещения тела за некоторый
определенный промежуток времени; сила в свою очередь приобретала векторный
характер. Но тогда сложение сил, приложенных к одному и тому же телу, сводилось
к сложению соответствующих скоростей, а так как законы сложения скоростей были
известны еще со времен Аристотеля, то появился знаменитый закон параллелограмма
сил. Трудно сказать, кто из механиков XVII в. первым установил этот закон; это
мог быть Джон Валлис (1616—1703), рассмотревший параллелепипед сил, или
французский механик Жиль-Персонн Роберваль
(1602—1675), применявший сложение и разложение сил по закону параллелограмма,
но можно проследить, как это было сделано.
Второй закон Ньютона в своей первоначальной форме
читается так: изменение движения (motus)
пропорционально приложенной силе и совершается по направлению той прямой, по
которой действует эта сила. Много спорили о точном переводе слова motus; так как это изменение имеет определенно векторный
характер, то под ним можно понимать только количество движения.
Доказательство закона параллелограмма имеется в первом
следствии из трех основных законов Ньютона.
Следствие 1.
При совокупных силах тело описывает диагональ параллелограмма в то же самое
время, что и его стороны при раздельных силах.
Если тело при действии в месте А (рис. 31) одной только силы М перенеслось бы в продолжение заданного
промежутка времени равномерным движением из А
в В и если
бы при действии в том же месте одной только силы N оно перенеслось бы из А
в С, то при действии обеих сил оно
перенесется в то же самое время из А
в D по диагонали параллелограмма ABCD.
Так как сила N
действует по направлению прямой АС,
параллельной BD, то по второму закону
эта сила нисколько не изменит той скорости приближения к прямой BD, которая была произведена первой
силой. Следовательно, тело в продолжение данного времени достигнет линии BD независимо от того, была сила N приложена или нет. На
основании такого же рассуждения к концу того же промежутка времени тело должно
находиться и где-либо на прямой CD,
следовательно, оно должно быть в их пересечении D. Переходит же оно из А в D прямолинейно на основании первого закона.
Следствие 2. Отсюда явствует составление силы,
направленной по AD из каких-либо двух
наклонных друг к другу АВ и BD, и наоборот, разложение любой силы,
направленной по AD, на наклонные АВ и BD.
Как это сложение, так и разложение беспрепятственно подтверждаются в учении о
машинах (механике).
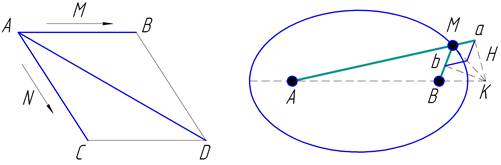
Рис. 31
Рис. 32
Вероятно, что приведенное Ньютоном доказательство
закона параллелограмма воспроизводит обычно употреблявшиеся рассуждения. Прежде
всего, статика не очень занимала Ньютона, основной целью которого было
динамическое обоснование планетных движений. Затем следует отметить стандартный
евклидовский стиль изложения: формулировка — построение — доказательство.
По существу, оно воспроизводит аристотелевский
параллелограмм скоростей, который тоже доказывался при помощи перемещений. В
действительности же между обоими параллелограммами имеется очень существенная
разница; можно представить, что на тело действуют две силы, но трудно
вообразить, что тело в данный момент имеет две скорости относительно одной и
той же системы отсчета. В аристотелевском доказательстве параллелограмма
скоростей очень ясно видно, что одна из складываемых скоростей переносная, а
другая относительная, тогда как в параллелограмме сил обе складываемые силы
совершенно равноправны.
Неправильное применение параллелограмма скоростей
может привести к очень серьезным ошибкам. Рассмотрим такой пример. Задача о
проведении касательных к кривым в XVII в. иногда решалась методом Роберваля. Он
заключался в том, что заданная кривая рассматривалась как траектория точки в
некотором движении: направление скорости этой точки и давало касательную.
Покажем, каким образом по методу Роберваля находится касательная к эллипсу
(рис. 32).
Эллипс определяется как геометрическое место точек М, сумма расстояний которых до фокусов А и В остается постоянной. Проведем радиусы-векторы AM
и ВМ. Можно считать, что перемещение Ма точки М по радиусу-вектору AM равно ее перемещению Mb
по радиусу-вектору MB. Построив
параллелограмм МаНb
на этих перемещениях (он будет ромбом), найдем, что представляющая направление
скорости диагональ МН является
биссектрисой угла аМb между
векторами, что соответствует действительности. Однако если нужно найти величину
соответствующей скорости, то она не будет равна МН.
Правильное решение. Точка М движется по прямой AM
со скоростью Ма относительно этой
прямой, а прямая AM совершает
переносное движение, вращаясь вокруг A.
Абсолютная скорость точки М равна
сумме относительной скорости Ма и
переносной, которая перпендикулярна к AM
и пойдет по аК. Рассматривая движение
М относительно радиуса MB, получим, что абсолютная скорость
точки М равна сумме относительной
скорости Mb и переносной, которая
пойдет по перпендикуляру bК. Отсюда получается, что истинная
скорость точки М изображается
диагональю МК не ромба МаНb, а
дельтоида МаКb. Направление скорости
точки М получилось правильным
вследствие того, что отношение скоростей Ма
и Mb равняется единице; если бы оно
отличалось от единицы, то оказалось бы неверным и направление скорости.
После Ньютона в XVIII в., начиная с Даниила Бернулли,
делается целый ряд попыток доказать закон параллелограмма совершенно
самостоятельно, ограничиваясь лишь чисто статическими понятиями.
В эпоху Ньютона геометрическая статика на плоскости
достигает своего, завершения. Современник Ньютона французский математик Вариньон
(1654—1722) в книге «Новая механика или статика», вышедшей после его смерти в
1725 г., изложил курс статики Плоской системы сил с техническими приложениями,
опираясь на закон параллелограмма сил и уравнение моментов. Закон
параллелограмма он так же, как и Ньютон, доказывал при помощи сложения движений
точки. Так как проспект курса Вариньона был представлен Парижской Академии в
1687 г. почти одновременно с выходом «Начал» Ньютона, то взаимное влияние двух
авторов является исключенным; доказательство Ньютона было общепринятым.
Вариньону принадлежит теорема о моменте равнодействующей плоской системы сил, а
также графический метод определения равнодействующей сил, лежащих в одной
плоскости, при помощи веревочного многоугольника. В книге «Новая механика или
статика» отдельно рассматривается определение условий равновесия на основании
принципа возможных перемещений.
После Вариньона отмечается застой в развитии
геометрической статики; все внимание механиков обращается на разработку
динамики, и притом аналитическими методами. Геометрические методы Вариньона
оказываются настолько забытыми, что в XIX в. инженер Кульман снова изобрел
метод веревочного многоугольника, который в некоторых книгах (например, в
ранних изданиях курса теоретической механики Николаи) так и называется методом
Кульмана.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов