Главная
Тема 18. Христиан
Гюйгенс. Нормальное ускорение. Центробежная сила. Маятник
Христиан
Гюйгенс (1629—1695) происходил из
рода, который принимал большое участие в политической и культурной жизни
Голландии. Его дед был секретарем героя освободительной борьбы Вильгельма I
Оранского, затем секретарем Государственного Совета при его брате Морице, которого он сопровождал в походах. Отец Гюйгенса —
Константин Гюйгенс, тоже служивший Оранскому дому секретарем штатгальтера, а
затем советником Вильгельмов II и III, хорошо был известен и вне Голландии. Он
получил великолепное образование: знал языки и литературу многих народов и
различных эпох и сам писал поэтические произведения по-латыни и по-голландски.
Он обладал научной любознательностью: интересовался математикой, механикой и
оптикой. Его друзьями было много замечательных людей различных национальностей,
в том числе и знаменитый Декарт, для которого в Голландии семья Гюйгенсов была
самой близкой; для Константина Гюйгенса Декарт даже написал целый трактат по
механике. Влияние Декарта сильно отразилось и на Христиане Гюйгенсе, особенно в
начале его жизни.
Христиан Гюйгенс вместе с братом получил хорошее
образование еще в доме: его учителем в области математики был Схоутен, познакомивший своего ученика с классическими
авторами античной математики Архимедом и Аполлонием,
а также и с произведениями Декарта. Оба брата очень много занимались по своей
инициативе и механическими искусствами: в частности, они много работали над
конструкцией астрономических инструментов; шлифованием сферических стекол
Гюйгенс занимался и в старости до тех пор, пока мог стоять у станка. Вращаясь в
кругу Декарта, молодой Гюйгенс находился в переписке с Мерсенном,
письма которого заменяли в то время современные научные журналы; от Мерсенна Гюйгенс узнал и о Галилее.
В 1646 г. в руки Гюйгенса попала книга Хуана Карамуэля Лобковича, бывшего
профессором богословия испанского университета в Алькала.
Лобкович отвергал установленные Галилеем законы падения
и заменил их своими, полученными из опыта; эти законы сводились к тому, что
пути, проходимые в первую, вторую, третью единицы времени, относились как числа
1, 2, 3. Гюйгенс, полагая, что опыт «часто обманывает», для закона Лобковича применил следующее рассуждение. Выберем в
качестве единицы длины путь, проходимый падающим телом в первую секунду; тогда
последовательные пути, проходимые в первую, вторую, третью секунды, будут равны
1, 2, 3 единицам длины, а весь путь представится суммой
![]()
В качестве единицы времени можно выбрать не одну
секунду, а две секунды; тогда пути, проходимые в последовательные новые единицы
времени, будут
![]()
![]()
![]() и т.д.
и т.д.
По закону Лобковича
требуется, чтобы они равнялись 3, 6, 12 и т. д. Полученное противоречие и
отрицает возможность существования такого закона. Исходя из требования
независимости от выбора единиц измерения, Гюйгенс, еще не знакомый с «Беседами
о двух новых науках» Галилея, находит, что пути, проходимые телом в
последовательные единицы времени, должны относиться как последовательные
нечетные числа 1,3, 5 и т. д.
Из всех древних математиков Гюйгенс больше всего ценил
Архимеда, о котором писал как о математике, ни с кем не
сравнимом.
Первыми самостоятельными произведениями Гюйгенса были
Сочинения: «О равновесии плавающих тел», опубликованное только в Полном
собрании его сочинений, и «О квадратуре круга» — оба они продолжали
исследования Архимеда. В дальнейшем его увлекла диоптрика — наука о преломлении
света, над которой он ,работал до конца своей жизни,
так и не приведя ее к окончательному завершению.
Требовательность Гюйгенса к своим произведениям была
исключительно большой; вследствие этого он во многих случаях потерял право на
приоритет открытий, чем и можно объяснить то обстоятельство, что он так и
остался сравнительно незаметным. Вместе с тем Гюйгенс смог построить настолько
хорошие телескопы, что с их помощью ему удалось открыть самый большой спутник
Сатурна Титан, а также установить наличие колец Сатурна. Оба эти открытия
сделали имя Гюйгенса известным для французских ученых.
К 1652 г. (Гюйгенсу в это время было 23 года)
относится сочинение «Об ударе тел», в котором он закончил исследование, начатое
не совсем удачно Декартом. И это сочинение осталось неопубликованным при жизни
Гюйгенса.
Прежде всего он указал
расхождение с действительностью правил, установленных Декартом для удара.
Основные аксиомы Гюйгенс формулирует так: если два
одинаковых тела движутся прямо навстречу друг другу с одинаковыми скоростями,
то каждое из них отскакивает с той же скоростью, какую оно имело до удара. Это
показывает, что Гюйгенс рассматривает так называемый абсолютно
упругий удар.
Следующая аксиома выражается так:
движения тел, а также и их скорости следует понимать равными между собой лишь
по отношению к другим телам, которые рассматриваются как бы покоящимися, хотя
эти тела вместе с первыми участвуют в другом общем движении. Поэтому если два тела движутся навстречу друг другу,
хотя они одновременно находятся, кроме того, и в другом равномерном движении,
то по. отношению к телу,
движущемуся общим с ними движением, удар между ними произойдет совершенно так
же, как при условии отсутствия добавочного общего движения.
С точки зрения современной физики, эта аксиома
формулирует принцип относительности в той форме, которая неправильно называется
принципом Галилея. Эта аксиома играет активную роль в доказательстве дальнейших
предложений; в частности, на обоих упомянутых аксиомах
основывается доказательство предложения 1: если в покоящееся тело ударяет
другое, одинаковое с ним, то после удара второе тело остановится, а то, которое
ранее покоилось, получит такую же
скорость, которая была у ударяющего тела.
Доказательство заключается в том, что удар,
происходящий неподвижной системе отсчета, рассматривается в другой системе,
движущейся со скоростью, равной той, которая первоначально имелась у одного из
ударяющихся тел.
В качестве третьей аксиомы Гюйгенс использует так
называемый принцип Торричелли: в движении тел, происходящем от действия их
тяжестей, общий центр тяжести этих тел не может подняться выше первоначального
положения.
При помощи этого принципа доказывается закон
сохранения живых сил при ударе: при взаимном ударе двух тел величина,
получающаяся после сложений величин каждого тела (его массы), помноженной на
квадрат его скорости до удара, равна той, которая получится после удара.
У Гюйгенса соответствующая величина mv2 (или ![]() ) еще не имеет названия; приблизительно через
пятьдесят лет Лейбниц назовет ее «живой силой».
) еще не имеет названия; приблизительно через
пятьдесят лет Лейбниц назовет ее «живой силой».
Таким образом, Гюйгенса надо поставить в начале
длинного ряда исследователей, работающих в установлении закона сохранения
энергии. За два года до смерти в 1695 г. он сформулировал его так: в любых
движениях тел ничего не теряется и не пропадает из сил, разве только в
определенном действии, для произведения которого требуется такое же количество
силы, какое и убыло. Силой же назовем потенцию, необходимую для поднятия груза.
Двойной силой будет та, которая может поднять один и тот же груз на вдвое
большую величину.
В данном случае имеется в виду лишь закон сохранения
механической энергии; это необходимое дополнение закона Декарта о сохранении
количества движения.
В 1668 г. Гюйгенс изложил теорию удара в Парижской
Академии наук; в конце того, же года вопрос об исследовании удара был поставлен
и в лондонском Королевском обществе, которое обратилось с просьбой о присылке
своих теорий к Гюйгенсу, Рену (Wren
— строитель Собора св. Павла в Лондоне) и Валлису.
Теория Рена, разработанная в
1660 г., оказалась в точности совпадающей с теорией
Гюйгенса; теория Валлиса рассматривала удар, который называется теперь
абсолютно неупругим.
С 1655 г. в творчестве Гюйгенса появилась новая тема,
вызвавшая большое количество исследований вплоть до самого конца его жизни. Эта
тема — конструкция точных часов — отвечала насущнейшей потребности, которую
ощущала не только Голландия, но и весь западный мир XVII в., особенно страны,
лежащие на побережье Атлантического океана.
Плавание в океане ставило для кораблевождения более
сложные задачи, чем в Средиземном море, где можно было держать курс по звездам.
В океане, где плавание продолжалось неделями и месяцами, чтобы не умереть от
голода и жажды, необходимо было точно знать положение в океане, иными словами,
долготу и широту Места нахождения. Определение широты места не представляло
больших затруднений: зная склонение Солнца для данного дня, можно было, измеряя
высоту Солнца над горизонтом в истинный полдень, определить с нужной точностью
и широту места.
С определением долготы было значительно труднее. В древности
«е определяли при помощи лунных затмений; если известно время затмения для
какого-нибудь основного пункта, допустим Гринвича, и определено время его
наступления для места своего нахождения, то по разности этих времен можно было
найти разность долгот между обоими местами, считая, что 1 ч разности
соответствует l5° долготы.
Вместо лунных затмений Галилей предполагал изучать
более часто наступающие затмения спутников Юпитера. Для этого следовало хорошо
знать их движения, кроме того, наблюдение за ними требует хорошей аппаратуры.
Проще было в качестве основного астрономического события рассматривать
прохождение Солнца через меридиан данного места (истинный полдень) и определять
его наступление по точным часам, поставленным по времени взятого основного
пункта; в таком случае задача сводилась к построению точных часов.
В средние века башенные часы приводились в движение
весом гири, равномерность опускания которой регулировалась последовательными
остановками колеса с зубцами. Галилей, определивший, что периоды небольших
колебаний маятника зависят только от его длины, а не от величины размахов,
предложил для этой цели маятник. К сожалению, он сам не успел построить часы;
его сын Винченцио начал строить модель таких часов,
но не закончил, так что сохранявшаяся в Тоскане модель не действовала.
Около 1635 г. Галилей предложил Генеральным Штатам
Голландии способ регулирования часов при помощи маятника, причем переписка шла
через отца Гюйгенса. Дело это ничем не кончилось, но более чем вероятно, что
Гюйгенс знал по крайней мере идею этого способа; во
всяком случае он построил вполне пригодные часы в 1657 г., чего Галилею сделать
не удалось.
Однако Гюйгенс на этом не остановился; он знал, что
величина периода колебания маятника в известной степени зависит и от амплитуды
его колебаний (Галилею это не было известно). Он попробовал другую систему
регулирования — при помощи конического маятника, вращающегося вокруг
вертикальной оси под определенным углом наклона к ней. Эта идея, как он сам
писал, возникла у него 5 октября 1659 г. Работая над ней, Гюйгенс написал одно
из самых важных своих произведений, а именно — трактат «О центробежной силе».
Введение в эту книгу начинается словами: тяжесть есть
стремление (conatus) опускаться вниз. Термин conatus для механика XVII в. означал движение, которое
готово совершиться, но почему-то еще не совершается. Лейбниц сравнивал
отношение conatus к совершившемуся движению с
отношением точки к линии, началом которой она служит. Когда тяжесть подвешена
на нить, то она натягивает нить вследствие того, что тяжелое тело стремится
двигаться по направлению нити равноускоренным движением известного вида.
В движении по наклонной плоскости conatus
во столько же раз меньше conatus'a по вертикали, во
сколько раз расстояние по наклонной плоскости, проходимое в одно и то же время,
меньше расстояния в движении по вертикали. Для числового определения соnatus'a нужно рассматривать
движение только в самом начале, взявши сколь угодно малый промежуток времени.
Основная идея Гюйгенса состоит в том, что силу надо
измерять не сообщенной ею скоростью в равномерном движении, а тем ускоренным
движением, которое получается под ее влиянием, т. е. действие силы измеряется
сообщаемым ей ускорением; (во времена Гюйгенса термин «ускорение» еще не
существовал, он появился только в первой половине XIX в.). По Гюйгенсу,
действие силы определяется движением, в котором пройденные пути пропорциональны
квадрату времени.
После этого Гюйгенс переходит к определению величины
центробежной силы (рис. 33). Посмотрим, какое и какой величины стремление
удалиться от центра имеется у тел, прикрепленных к вращающейся нити или колесу.
Пусть колесо BG вращается в
горизонтальной плоскости вокруг центра А; если к его окружности привязан шарик, то он, придя в
точку В, стремится двигаться по прямой
ВН, касательной в точке В к колесу. Здесь с первого взгляда
трудно представить, по какой же причине натягивается нить AB, если шарик стремится двигаться по прямой ВН, перпендикулярной к направлению нити АВ.
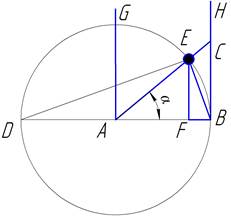
Рис. 33
Дальнейшие рассуждения можно привести уже в
современной терминологии. Пусть окружная скорость шарика v, и за бесконечно малое время t
радиус АВ повернется на угол α,
а оторвавшийся шарик, двигаясь прямолинейно, пройдёт отрезок ВС = vt.
Перемещение шарика относительно колеса BG
по радиусу равно ЕС = s. Ввиду малости
а можно считать, что ЕС равно своей
проекции FB на радиус АВ. Соединив Е с концами В и D диаметра, получим
прямоугольный треугольник BED, в
котором
![]()
где
R — радиус колеса.
Так
как BE ![]() . ВС = vt,
то
. ВС = vt,
то
![]()
получено равноускоренное движение с ускорением v2/R.
Гюйгенс вычисление заканчивает утверждением, что это
стремление совершенно подобно тому, которое ощущается, когда шарик Удерживается подвешенным на нити, так как и в этом случае
он тоже стремится уйти равноускоренным движением по направлению самой нити.
Гюйгенс определяет также траекторию относительного
движения шарика С. Ее можем легко
получить, применив принцип Коперника: сообщим одновременно колесу BG и прямой ВН вращение колеса в противоположную сторону; тогда колесо
остановится, а прямая ВН будет
перекатываться по нему без скольжения, причем точка С удаляется по этой прямой с постоянной скоростью v, иными словами, расстояние СВ возрастает
пропорционально углу поворота.
Траектория, описанная точкой С, является эвольвентой
окружности. Так создалась теория эвольвент, которая была позже специально
рассмотрена Гюйгенсом в одном из отделов его «Ноrologium
oscillatorium» (в русском переводе «Маятниковые часы»).
Гюйгенс считает, что описанное стремление совершенно подобно тому, с каким подвешенные на нити тяжелые
тела стремятся двигаться вниз. Отсюда получаем, что центробежные силы неравных
тел, движущихся с одинаковой скоростью по равным кругам, относятся между собой
как тяжести движущихся тел или их массы (quantitates solidae — количества
твердого вещества).
Гюйгенс показал, что определенный им conatus, по
существу, принадлежит к тому же классу, что и сила тяжести. Отсюда в дальнейшем
получается некоторое колебание в терминологии: иногда употребляют conatus
centrifugus (центробежное стремление), иногда же vis centrifuga (центробежная
сила).
Центробежная сила, растягивающая нить, с современной
точки зрения представляет не что иное, как приложенную к связям реальную силу
инерции.
Подобно тому как подвешенный
на нити груз уравновешивается реальной силой ее натяжения, так и вращающийся в
горизонтальной плоскости прикрепленный к нити груз подвержен действию некоторой
центростремительной силы. Следовательно, инерционное у Аристотеля круговое
равномерное движение производится некоторой силой, т. е. оказывается движением
насильственным; это второй и окончательный удар по аристотелевой динамике,
которая затем сменится динамикой Ньютона (первый удар был нанесен Галилеем).
Если равноускоренное движение по закону s = (at2)/2
заменить современным термином «движение с ускорением а», то получим формулировку второго закона Ньютона: сила
пропорциональна массе тела и сообщаемому ею этому телу ускорению.
Наконец, Гюйгенс рассматривал случай относительного
движения. Сила инерции, отсутствующая для шарика в неподвижной системе отсчета,
оказалась реальной в переносной системе отсчета — колесе BG. Это обстоятельство тоже было известно Гюйгенсу, так как он
учитывал влияние вращения Земли на период колебаний маятника на различных
широтах, т. е. знал, что ускорение силы тяжести g изменяется с широтой.
Таким образом, первый и второй законы Ньютона уже были
известны Гюйгенсу. Остается неизвестным, знал ли он третий закон. Возможно, что
он имел о нем некоторое представление, но во всяком
случае он его не формулировал. Но даже и первых двух законов вполне достаточно
для изложения динамики свободной материальной точки.
Первые четыре предложения остальной части
рассматриваемой книги в современном обозначении сводятся к выводу формулы для
центробежной силы:
![]()
В пятом предложении решается задача: если тело
движется по окружности со скоростью, получающейся при падении с высоты, равной
четверти диаметра, то это тело имеет центробежное стремление, равное своей
тяжести.
Гюйгенс пытался определить, в каком
отношении время наименьшего колебания маятника находится со временем падения по
вертикальной прямой с высоты, соответствующей маятнику. Это дало возможность сделать открытия относительно
циклоиды.
В успешном решении этой задачи Гюйгенсу помогла
счастливая случайность. За полтора года до рассматриваемого времени, в июне
1658 г., Гюйгенсу прислали из Франции сделанный неизвестным лицом вызов решить
некоторые задачи. Этим неизвестным лицом был великий французский писатель и
математик Блэз Паскаль (1623—1662), а
предложенные задачи касались циклоиды. Через любую точку
циклоиды параллельно ее основанию проводилась прямая до ее пересечения с осью
циклоиды., Требовалось найти площадь и центр тяжести фигуры, заключенной между
кривой, проведенной прямой и отрезком оси, а также объемы и центры тяжести тел
вращения полученного сегмента вокруг его прямолинейных сторон и, наконец,
центры тяжести половинок этих тел вращения, полученных в результате пересечения
их плоскостью, проведенной через ось циклоиды.
Гюйгенс тоже принимал участие в решении этих задач и
удостоился похвального отзыва Паскаля, который вместе с окончательным решением
задачи дал и обзор присланных ему решений. В дальнейшем Гюйгенс продолжал
заниматься циклоидой и, в частности, указал некоторые свойства касательной к
циклоиде, которые ему пригодились впоследствии.
Исследуя свойства предполагаемой кривой, по которой
должны были совершаться изохронные колебания, он нашел, что этим свойствам
вполне удовлетворяет циклоида. Одновременно ему удалось определить и полный
период малых колебаний маятника, получив известную формулу
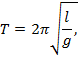
где
l— длина маятника, g — ускорение силы
тяжести, или, по Гюйгенсу, коэффициент пропорциональности в формуле,
определяющей закон падения тяжелого тела без начальной скорости.
Сконструированный им циклоидальный маятник представлял
собой тяжелый груз, подвешенный на нити, который колебался между двумя
пластинками АВ и АС (рис. 34). Форму их он сначала определял опытным путем, а затем
установил, что эти пластинки должны быть изогнуты по циклоиде, так как
эвольвента циклоиды является тоже циклоидой.
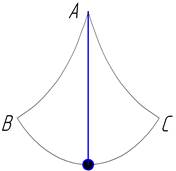
Рис. 34
С 1660 г. начинаются поездки Гюйгенса в Париж, а затем
в Лондон, где он познакомился с членами английского Королевского общества. В
это время производилась дальнейшая работа по усовершенствованию конструкции маятника.
Так как реальный маятник имеет форму чечевицы значительных размеров, a его
стержень не является невесомым, то надо было решить задачу о периоде колебаний
физического маятника.
Наиболее простым решением этой задачи было такое:
рассматриваемый физический маятник надо заменить математическим с той же точкой
привеса и с одинаковым периодом колебания. Если длину такого
маятника отложить от точки привеса по оси физического маятника (по проведенному
из центра его тяжести перпендикуляру к оси привеса), то конечная точка
отложенного отрезка получает название центра качания; в нем как бы
сосредоточивается вся масса физического маятника.
Эта задача ставилась перед Гюйгенсом еще в ранний
период, но в несколько отличной форме, а именно в определении так называемого
центра удара. Вопрос стоял так: будет ли удар мечом более действенным, если он
произведен местом, находящимся около острия, или же какой-нибудь другой точкой,
местом около центра тяжести либо даже вблизи рукоятки?
Решение итальянского механика Бальди (1553—1617),
поставившего этот вопрос, было таким: нужно ударять местом около центра
тяжести. Мерсенн, написавши об этом Гюйгенсу, считал, что центр удара должен
совпадать с центром качания подвешенных тел, и по совету Декарта определял его
опытным путем, находя такую длину нити с подвешенным грузом, при которой ее
колебания с грузом совершались бы в одинаковое время с колебаниями подвешенного
плоского тела. На письме Мерсенна, написанном в 1646 г., Гюйгенс сделал
пометку: «Я нашел это правило в 1664 году».
Решение этой задачи Гюйгенс получил на основании
установленного им закона сохранения механической энергии, т. е. с применением
интеграла живых сил.
В формулу приведенной длины l физического маятника входит момент инерции J относительно оси привеса:
![]()
где
Ма — произведение массы фигуры на
расстояние от ее центра тяжести до оси привеса (статический момент).
Если маятник представлял однородную плоскую фигуру,
колеблющуюся около оси, перпендикулярной к плоскости фигуры, то Гюйгенс считал
массы всех составляющих ее точек равными единице; приведенная длина выражалась
формулой
![]() ,
,
где
Оа, Ob, ... — расстояния этих точек до оси привеса.
Если рассматриваемая фигура была
плоской и ось привеса находилась в этой плоскости, то для решения задачи надо
было построить на этой плоскости цилиндр, основанием которого была
рассматриваемая фигура, рассечь его плоскостью, проходящей через ось вращения
под углом в 45° с плоскостью фигуры, и искать центр тяжести полученного
усеченного цилиндра, или, как его называл Гюйгенс, «копытца». После нахождения этого центра тяжести центр качания
получался в основании перпендикуляра, опущенного из него на плоскость заданной
фигуры.
Таким методом Гюйгенс определял центр качания
различных фигур и тел, подвешенных различным образом, и, что всего труднее,
шара, подвешенного на нити. Так как все внимание Гюйгенса сосредоточивалось на
определении центра качания, то понятие о моменте инерции от него ускользнуло и
осталось только окончательное правило — известное построение Гюйгенса для
определения центра качания на прямой, проходящей через центр тяжести и точку
привеса.
Результаты своих исследований Гюйгенс опубликовал в
книге «Часы с маятником», вышедшей в свет в 1673 г. Кроме описания часов, в эту
книгу вошла теория циклоидального маятника, учение об эволютах и эвольвентах и
общие методы определения центра качания. В конце книги Гюйгенс поместил без
доказательств теоремы, касающиеся центробежной силы; по-видимому, он не считал
этот вопрос разработанным до конца. Эти теоремы н.е
были включены в составленный Гюйгенсом список произведений, которые он завещал
опубликовать после его смерти; однако эта книга была опубликована. Но даже и в
составе «Часов с маятником» она сыграла очень большую роль в дальнейшем
развитии физико-математических наук. Так как в ней была впервые установлена
величина центростремительного ускорения, то Ньютон получил возможность
определить силы, с которыми Солнце действует на окружающие его планеты. Эта
работа Гюйгенса, а также три закона Кеплера составили основу, на которой Ньютон
создал свою классическую динамику.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21