Главная
Тема 19. Исаак
Ньютон. Три закона движения
В 70-х годах XVII в. на горизонте западноевропейской
науки появляется еще одно яркое светило — Исаак Ньютон (1643—1727), которому удалось
в разработке классической механики сделать больше, чем оба его великих
предшественника, взятые вместе. Жизнь его значительно беднее событиями, чем у
Гюйгенса, который был членом Парижской Академии наук и провел в Париже много
времени — от 1666 до 1681 г., впервые посетил Англию в 1661 г. и был деятельным
членом Королевского общества вплоть до 1678 г.
Ньютон родился в Англии, в графстве Линкольн, получил
образование в Кембридже и начиная с 1688 г. был связан
с Лондоном; с 1695 гм он был назначен хранителем Монетного двора. Жизнь его
протекала спокойно, мирно однообразно; умер он неженатым, никуда не выезжал за
пределы Англии. Путешествия его ограничивались небольшими расстояниями от Грэнтэма, где он учился в начальной школе, до Кембриджа,
где он получил высшее образование, и Лондона (около 200 км). Ньютон отличался
редким здоровьем, никогда не имел особенно близких друзей-ровесников; чисто
«житейская» биография Ньютона почти ограничивается послужным списком, да
десятком анекдотов-легенд.
С 1661 по 1669 г. Ньютон учился в Кембридже, в И.
Ньютон (1643—1727) 1669 г. он занял место профессора математики, заменив своего
учителя Барроу; в 1672 г. был избран в члены
Королевского общества. В 1664—1667 гг. он, опасаясь чумы, уехал на свою родину
в деревню Вульсторп и в эти 2—3 года создал
математический анализ, новую оптику и основанную на принципе всемирного
тяготения новую планетную систему. Дальнейшая жизнь Ньютона была лишь
разработкой идей, сложившихся у него в тиши деревенского уединения.
В 1672 г. вышла из печати книга «Оптика» с изложением ньютоновой теории цветов; весь конец 1672 г. и первую
половину 1673 г. он ведет дискуссию с Гюйгенсом, интересную в том отношении,
что в ней выявляется противоположность характеров научного мышления двух
великих людей. Не оспаривая ценности опытов Ньютона, Гюйгенс видел очень
большую трудность в том, как при помощи механических теорий физики объяснить
различие цветов.
В письме от 14 января 1673 г. к секретарю Королевского
общества Ольденбургу Гюйгенс писал:
«Мне кажется, что самое серьезное возражение...
заключается в том, действительно ли существуют более чем два цвета. Что
касается меня, то я уверен, что единственная гипотеза, объясняющая механически
и из природы движения желтый и синий цвета, будет достаточной и для всех
других... Точно так же я не вижу, почему мистер Ньютон не удовлетворится двумя
цветами; ведь было бы гораздо легче найти какую-нибудь гипотезу, которая
объяснила бы из свойств движения различия этих двух
цветов, чем искать причины такого разнообразия для других цветов».
На это Ньютон (тоже в письме к Ольденбургу) возражал:
«Рассматривать, каким образом можно объяснить цвета
при помощи гипотез, не входит в мои планы. Я никогда не намеревался показать, в
чем заключается физическая сущность цветов и их различий; мне нужно было только
показать, что цвета фактически являются первоначальными и неизменными
свойствами лучей, их имеющих. Я предоставляю другими механическими гипотезами
объяснять природу и различия этих качеств, что, как я думаю, будет делом нетрудным».
В это время Ньютон получил от Гюйгенса экземпляр
«Часов с маятником» и написал (3 июля 1673 г.) Ольденбургу письмо,
предназначавшееся для передачи Гюйгенсу:
«Я С большим удовольствием смотрел эту книгу и нашел,
что она полна весьма изящных и полезных рассуждений, вполне достойных их
автора. Я рад, что мы Должны ждать появления еще одного трактата «О
центробежной силе», рассуждения которого могут оказаться очень полезными для
философии природы, астрономии и механики».
Ньютон затем критикует взгляды Гюйгенса на природу
цветов; если белый цвет состоит только из двух цветов, то его можно и разложить
только на два цвета.
Ньютон сделал окончательное резюме своей теории
цветов, из которой достаточно привести лишь един
тезис:
«Различными цветами я называю не только наиболее
обычные, как, например, желтый, зеленый, синий, коричневый, но и все другие
мельчайшие градации, совершенно так же, как и в музыке существуют не только
наиболее обычные тона, но различными звуками называются и все наименьшие
градации».
Как близок был Ньютон к тому, чтобы определить, в чем
заключается физическая сущность различных цветов (длина волны или период
соответствующего колебания)!
Интересно, что в дальнейшем Гюйгенс начал заниматься
общей теорией гармонических колебаний; разработку этой теории он до конца не
довел, и конечно, не опубликовал. Вероятно, к этому и к следующему году
относятся занятия Гюйгенса теорией музыки, результаты которых тоже не были
опубликованы.
Конец 70-х годов XVII в. Гюйгенс посвятил работе над
микроскопом, с которым он познакомился во время пребывания в Голландии у основателя микроскопии Левенгука (1632—1723); он
построил свой микроскоп, который произвел фурор во Франции. Кроме того, он
занимался и разработкой своей волновой теории света, в частности недавно открытого
двойного лучепреломления света в кристаллах исландского шпата. В результате его
работ появился «Трактат о свете», написанный по-французски и, как обычно у
Гюйгенса, вышедший с большим запозданием — в 1690 г. Для механики эта работа
имеет значение, как первый пример исследования движений в сплошной среде.
Гюйгенс рассматривал свет, прежде всего как движение.
Нельзя сомневаться, что свет представляет движение некоторой материи. На это
указывают разрушение тел в фокусе зажигательного стекла и действующие на нерв
зрительные впечатления, обусловленные тем, что между ним и светящимся телом
находится некоторая материя. Световые колебаний объясняются упругостью частичек
эфира, которые не должны иметь сферической формы, но обязательно должны быть
одинаковыми; в противном случае по законам теории удара, испытывающие удар
частички не могли бы остановиться, а получали бы движение вперед или назад.
Гюйгенс вспоминает известный из
теории удара факт, что, когда шарик налетает с некоторой скоростью на другой
покоящийся обладающий одинаковой с ним массой, то он останавливается, а
ударенный получает скорость ударившего шарика. Затем он указывал, что два шарика могут обменяться
своими скоростями даже и в том случае, когда они непосредственно не
соприкасаются, а именно через посредство промежуточных шариков. Этот взаимный
обмен скоростями объяснял, по Гюйгенсу, возможность одновременного
распространения через одну и ту же область нескольких различных световых лучей.
После этого он сформулировал
знаменитый принцип: при испускании световых волн следует иметь в виду, что
каждая частичка материи, в которой распространяется волна, должна сообщать свое
движение не только ближайшей частичке, находящейся на одной прямой с первой
частичкой и источником света; она также необходимо сообщает его всем частичкам,
которые соприкасаются с ней и препятствуют ее движению. Таким образом, необходимо, чтобы вокруг каждой
частички зарождалась волна, центр которой был в этой частичке.
На основании этого принципа Гюйгенс объяснил, как
происходит отражение и преломление света. Так как Гюйгенсу уже было известно
открытие Ремером величины скорости света, то для
объяснения преломления света он принял, что в телах свет распространяется с
меньшей скоростью, чем в эфире. Двойное лучепреломление Гюйгенс объяснил тем,
что при вступлении в кристалл исландского шпата луч распадается на два луча.
Для одного из таких лучей соблюдаются законы обычного преломления (ординарный
луч), для других же (экстраординарный луч) они не
соблюдаются. Гюйгенс пришел к заключению, что также существовали две различные
эманации световых волн. Одну из них он видел в наблюдающемся в этом камне
правильном преломлении, предполагая, что для этой эманации волны имеют обычную
сферическую форму. Что касается другой эманации, которая должна была произвести
неправильное преломление, то он пытался определить, что могут произвести
эллиптические или сфероидальные волны.
Для таких сфероидальных волн (в виде эллипсоида
вращения) скорость распространения света в кристалле не является одинаковой во
всех направлениях.
И в этом отношении Ньютон оказался на противоположных
позициях с Гюйгенсом. Его теория предполагала, что свет распространяется в виде
мельчайших частиц, свободно рассеивающихся как в пустом пространстве, так и в
материальных телах, в которых скорость распространения света больше, чем в
пустом пространстве. Дискуссии по этому вопросу, по существу, не было, так как
после опубликования «Трактата о свете» Гюйгенс жил всего лишь пять лет.
Благодаря колоссальному авторитету Ньютона в XVIII в.
наибольшим успехом пользовалась его корпускулярная теория света; но в XIX в.
было установлено, что скорость света в телах меньше скорости света в пустоте, и
победа оказалась на стороне Гюйгенса.
В настоящее время взгляды обоих великих ученых
оказались правильными — световой фотон является одновременно и частицей и
волной.
В 1686 г. вышло в свет одно из самых выдающихся
произведений мировой научной литературы — первое издание книги Ньютона
«Математические начала натуральной философии». Целью этого произведения было
создание вполне разработанной системы Вселенной, основанной на законе
всемирного тяготения. В нем Ньютон дал решение задачи, которая мучила
европейский, и не только европейский, мир.
Строение Солнечной системы и законы движения планет
изложены в третьей книге сочинения, озаглавленной «О системе мира», первые же
две книг» посвящены непосредственно теоретической механике. Эти книги имеют
«Введение», которое представляет тем больший интерес, что в нем излагаются
основы ньютоновской механики.
Это «Введение» распадается на две части: в первой
даются определения основных понятий, во второй устанавливаются законы движения.
Первое определение читается так: количество материи измеряется в совокупности
ее плотностью и объемом, т. е. их произведением.
Это количество материи он называет массой и указывает,
что она является известной» если дан вес тела. А что масса пропорциональна весу
тела, он нашел при помощи очень точно поставленных опытов с маятником.
Разгадка этого определения заключается в том, что
Ньютону нужно было указать разницу между весом, рассматриваемым как сила, и
массой. До Ньютона вес применялся только в статике как сила, движущая или
сопротивляющаяся, т. е. как векторная величина. В динамике же вес тела играет
совершенно другую роль — он используется как скалярная величина, входящая в
определение количества движения. Плотность сейчас является производной
величиной и измеряется частном от деления массы на объем; в XVII в.
первоначальной величиной была плотность (удельный вес), правила определения которой были известны со времен Архимеда, тогда
как понятие «масса» было новым.
Затем Ньютон определил количество движения (motus); оно измеряется скоростью и количеством материи в
совокупности, т. е. их произведением.
Интересно третье определение: материя обладает
возможностью сопротивления; поэтому каждое тело, поскольку оно ею обладает,
стремится оставаться в состоянии покоя или равномерного и прямолинейного
движения.
Эта сила постоянно пропорциональна массе тела и от
инерции материи отличается только способом рассмотрения. Инерция материи
производит то, что каждое тело только с трудом может быть выведено из своего
состояния покоя или движения; поэтому эту присущую материи силу (vis insita) можно назвать силой
инерции.
Эта сила инерции «дожила» до времени Эйлера, поскольку
в течение всего XVIII в. понятие о силе было весьма неопределенным; применяли
термины «живая сила», «лошадиная сила», « жизненная сила», «усыпительная сила»
и т. д. Точное определение понятия силы выработалось только к началу XIX в.,
хотя уже Д'Аламбер подозревал, что эта «сила инерции» все же не
совсем сила.
Настоящая сила (в современном смысле) появляется
только в четвертом определении: приложенная сила (vis
impressa) есть действующее на некоторое тело
стремление изменить его состояние покоя или равномерного и прямолинейного
движения.
Затем Ньютон дает определение центральной силе, для
которой характерным является центр действия силы. К числу таких сил относятся
тяжесть, магнитная сила, всемирное тяготение, а также сила, противодействующая
той, с которой вращающийся на веревке камень стремится оторваться от нее.
Величина центростремительной силы бывает троякого
рода: абсолютная, ускоряющая и движущая. Абсолютной величиной
центростремительной силы является большая или меньшая мера ее, зависящая от
действующей причины, исходящей из центра, и распространяющаяся к окружающим
частям. Ускоряющая величина центростремительной силы пропорциональна той
скорости, которую она порождает в заданное время. Движущая величина
центростремительной силы пропорциональна движению, которое она порождает в
заданное время.
Ньютон применил соответствующие определения только к
центральным силам, но их можно было выразить и в более общей форме. Составим
уравнение
![]()
В этом уравнении F
представляет собой то, что Ньютон называет абсолютной силой; ![]() — изменение
количества движения в единицу времени, которое он назвал движущей силой, а
— изменение
количества движения в единицу времени, которое он назвал движущей силой, а ![]() — ускоряющей силой.
— ускоряющей силой.
Понятие ускоряющей силы Ньютон получил исходя из того
факта, что все тяжелые тела падают с одним и тем же ускорением g. Он писал о
том, что вблизи земной поверхности, где ускоряющая сила, т. е. сила тяжести, во
всех телах одна и та же, движущие силы тяжести, или веса, относятся как массы.
Если же подняться в области, где ускоряющая сила тяжести меньше, то в такой же
мере уменьшится и вес, который всегда пропорционален произведению ускоряющей
силы тяжести на массу тела.
Как видно, Ньютон был близок к современному
определению силы как произведения массы на ускорение; его удержало лишь
введенное им понятие об ускоряющей силе, которую А. Н. Крылов назвал, несколько
модернизируя, напряжением силы тяжести.
В течение всего XVIII в. ускоряющая сила F/m заслонила понятие ускорения; даже
через сто лет после Ньютона Лагранж в своей «Аналитической механике» называет ![]() ускоряющей
силой но оси Ох.
ускоряющей
силой но оси Ох.
Ньютон дал также определение
абсолютного и относительного пространства и времени, а также установил различия
между абсолютным и относительным движениями. Он указал, что действующие силы сами по себе еще не
могут определить, будет ли данное движение относительным или нет. Каждое
относительное движение может поэтому изменяться, в то
время как истинное остается неизменным.
Проявления, которыми различаются абсолютное
и относительное движения, состоят в силах стремления от оси вращательного
движения, ибо в чисто относительном вращательном движении эти силы равны нулю,
в истинном же и абсолютном они больше или меньше, сообразно количеству
движения.
Если на длинной нити подвесить сосуд и, вращая его,
закрутить нить, пока она не станет совсем жесткой, затем наполнить сосуд водой
и, удержав сперва вместе с водой в покое, пустить, то
под действием появляющейся силы сосуд начнет вращаться, и это вращение
поддерживается достаточно долго раскручиванием, нити. Сперва
поверхность воды остается плоской, как было до движения сосуда. Затем сосуд
силой, постепенно действующей на воду, заставляет и ее участвовать в своем
вращении.
По мере возрастания вращения вода постепенно отступает
от середины сосуда и возвышается по его краям, принимая впалую форму
поверхности; при усиливающемся движении она все более и более поднимается к
краям, пока не станет обращаться в одинаковое время с сосудом и придет по
отношению к сосуду в относительный покой. Этот подъем воды указывает на
стремление ее частиц удалиться от оси вращения, и по этому стремлению
обнаруживается и измеряется истинное и абсолютное вращательное движение воды,
которое, как видно, во всем совершенно противоположно относительному движению.
В начале, когда относительное движение воды в сосуде
наибольшее, оно совершенно не вызывает стремления удалиться от оси — вода не
стремится к окружности и не повышается у стенок сосуда, а ее поверхность
остается плоской и ее истинное вращательное движение еще не начинается. Затем,
когда относительное движение уменьшается, повышение воды у стенок сосуда
обнаруживает ее стремление удалиться от оси, и это стремление показывает
постепенно возрастающее истинное вращательное движение, и когда оно становится
наибольшим, то вода устанавливается в покое относительно сосуда.
Таким образом, это стремление не зависит от движения
воды относительно окружающего тела; следовательно, по таким движениям нельзя
определить истинного вращательного движения тела. Истинное круговое движение какого-либо
тела может быть лишь одно в полном соответствии с силой стремления его от оси;
относительных же движений в зависимости от того, к чему они относятся, тело
может иметь бесконечное множество; но независимо от этих отношений такие
движения совершенно не сопровождайся истинными проявлениями, если только это
тело не обладает кроме этих относительных также и упомянутым единственным
истинным движением.
После определения понятий Ньютон в книге
«Математически начала натуральной философии» изложил следующие аксиомы, или
законы, движения:
1. Все тела
упорствуют в своем состоянии покоя или равномерного прямолинейного движения,
пока не будут принуждены приложенными силами изменить свое состояние.
2. Изменение
движения пропорционально приложенной движущей силе и совершается по прямой
линии, по которой прилагается эта сила.
3. Действию
всегда соответствует противоположное и равное противодействие, или
взаимодействия двух тел между собой всегда равны и направлены в противоположные
стороны.
По существу, два первых закона были уже сформулированы
Ньютоном выше; второй закон для центростремительных сил был дан Ньютоном в гораздо более конкретной и близкой к современной форме. Формулировка второго закона, в которую входит понятие о количестве
движения, очень близка к той, которую мог бы дать Декарт, если бы ввел понятие
о силе, векторный характер которой был ему неизвестен.
Понятие о центростремительной силе было тесно связано
с вопросом о тяготении, который рассматривался в течение всего XVII в. Декарт
объяснял существующую на земной поверхности тяжесть окружающим Землю вихрем,
отбрасывающим к ее центру тела, находящиеся на ее поверхности. Он не только не
признавал тяготения между небесными телами, но даже допускал мысль, что птицы,
летящие очень высоко над поверхностью Земли, могут выйти из сферы действия
тяжести, и ставил вопрос, вернется ли на Землю ядро, выпущенное вертикально из
пушки.
В 1669 г. во Французской Академии
происходила дискуссия о причинах тяготения; некоторые из выступавших допускали действие
на расстоянии, но все же наилучшим был признан доклад Гюйгенса, отвергавшего
действие на расстоянии. В 1690 г.,
когда Гюйгенс уже познакомился с книгой Ньютона «Математические начала
натуральной философии», он писал о том, что он не согласен с принципом, который
Ньютон кладет в основу своих вычислений; что все малые частицы взаимно
притягиваются и стремятся сблизиться. Гюйгенс убежден, что причина такого
притяжения не может быть объяснена при помощи какого-нибудь механического
принципа или закона движения.
Он не был против «центростремительной силы», при
помощи которой Ньютон заставляет планеты тяготеть к Солнцу, а Луну к Земле.
Существование такого рода притяжения, или импульса в природе доказывается не
только опытом, но и может быть объяснено на основании законов движения (теория
вихрей Декарта).
Когда-то Гюйгенс предполагал, что сферическая форма
Солнца может произойти от действия той же самой причины, которая вызывает
сферичность Земли, но не распространял действия тяжести на такие расстояния, как
от Солнца до планет или от Земли до Луны. Точно так же Гюйгенс не думал о
закономерном уменьшении тятогения, обратно
пропорциональном квадратам расстояний.
Допущение такого тяготения к Солнцу,
убывающего в указанной пропорции, производит настолько хорошее уравновешивание
центробежных сил планет, что получается то самое эллиптическое движение,
которое Кеплер угадал и подтвердил своими наблюдениями; поэтому нельзя
сомневаться в правильности упомянутых выше гипотез относительно тяготения, а
также и в правильности системы Ньютона в той мере, как она на них основывается. Это тем более должно казаться справедливым, что она
дает решение многих трудностей, которые не могли быть преодолены при помощи
вихрей, предполагаемых Декартом.
Гюйгенс принял всю математическую часть
астрономической системы Ньютона, сделав только оговорку относительно действия
на расстояния. Но из этого не следует, что он согласился с обоснованием его
механической системы, иными словами, с его тремя законами движения, или,
точнее, с первым законом.
Он был твердо убежден, что всякое движение совершается
относительно какого-либо материального тела и что абсолютное пространство не
может быть принято в качестве системы отсчета. Если считать нелепым, чтобы оно
находилось в движении, то неужели из этого должно следовать, что оно
обязательно является неподвижным.
По отношению к абсолютному пространству понятия о
покое и движении неприложимы. Равным образом, об изолированном теле в
пространстве, где не имеется никаких других действующих на него тел, нельзя
утверждать, будет ли оно двигаться или находиться в покое, поскольку не
существует никаких других материальных тел, которые могли бы служить в качестве
системы отсчета.
Невозможно определить абсолютность равномерного
прямолинейного движения, но относительно вращения, или кругового движения,
Ньютон, как показано выше, держался другого мнения. Такого мнения долго
придерживался и Гюйгенс, определявший влияние центробежной силы на величину
ускорения силы тяжести на различных широтах и также приписывавший сплюснутость Земли именно развивающимся при ее вращении
центробежным силам. Однако под конец жизни он изменил это мнение.
Эксперимент, на который ссылался Ньютон, есть
описанный выше опыт с вращающимся сосудом, наполненным водой. Эрнст Мах в
«Очерках по истории механики» указал, что причиной поднятия воды у стенок
сосуда является все же относительное движение воды по отношению к совокупности
неподвижных звезд и что совершенно неизвестно, какие явления наблюдались бы,
если бы ведро с водой было неподвижным, а вокруг вращалась вся совокупность
неподвижных звезд.
Всей силы своего замечания Мах не представлял, но
через несколько десятков лет это место его книги попало на
глаза гениального мыслителя Альберта Эйнштейна и было для него толчком
созданию общей теории относительности.
Невозможность признания первого закона Ньютона,
по-видимому, и была для Гюйгенса причиной, по которой он не смог создать полной
системы механики. Хотя известно теперь, что в данном вопросе прав Гюйгенс, а не
Ньютон, но все же «гениальная ограниченность» Ньютона позволила ему создать
систему механики, на которой основаны почти все технические достижения двух
столетий.
Некоторые недоразумения были и со вторым законом.
В настоящее время нет никакого сомнения, что под motus (движение) Ньютон понимал «количество движения»;
произведенный выше анализ его определений «величин» центростремительной силы
показывает, что он понимал это со всей ясностью. Но для его современников
понятие о векторной величине было неизвестно, и его motus
можно было понимать и иначе. Возникла целая школа механиков, которые считали,
что motus надо понимать не как то, а как mv2; в возникшей дискуссии
принял участие Вольтер, который содействовал распространению ньютонианизма во Франции. Дело осложнилось тем, что когда
на основании указанных двух вполне различных принципов решалась конкретная
задача, то при правильном решении результаты получались одинаковыми. Такое
положение продолжалось до середины XVIII в., когда Д'Аламбер показал, что в
данном случае, по существу, обе стороны по своему правы, но и та и другая не
вполне.
Для нас все дело заключается в следующем: количество
движения есть векторная величина, живая сила — скалярная. Если речь идет о
прямолинейных движениях, с которых большей частью и начинали механики XVIII в.,
то количество Движения можно понимать и как алгебраическую величину. Затем,
когда речь идет об «изменении» какой-либо величины, то необходимо указать
независимую переменную, по отношению к которой отсчитываются изменения. Для
выражения количества движения такой переменной является время и, как показано
выше, Ньютон это хорошо знал:
![]()
Для кинетической энергии независимой является
координата х в прямолинейном движении
![]()
Оба полученных равенства вполне справедливы; каждое из
них имеет свою область применения.
Теперь проследим, каким образом Ньютон применял свои
принципы на практике. Первой задачей, которую он решил, была следующая: зная
законы движения планет, определить силу, которая производит их движение. В
настоящее время известно, что Ньютон решил задачу на основании созданного им
анализа бесконечно малых; но ее решение он записал обычным в то время
геометрическим, методом. Сейчас решение этой задачи можно произвести при помощи
анализа бесконечно малых.
Законы движения планет, как известно, были даны
Кеплером. Первых два закона утверждают, что планеты
движутся по эллипсам, в одном из фокусов которых находится Солнце, и что
радиусы - векторы планет, имеющие начало в Солнце, описывают площади
пропорционально времени, т. е. с постоянной секторной скоростью.
Так как планеты движутся вечно и не встречают
заметного сопротивления, то наиболее естественно предположить, что движущая
сила не изменяется в зависимости от времени и не зависит от скорости движения
планет.
Пусть АВ —
большая ось эллипса, по которому движется планета (рис. 35), С —его центр, О —фокус, OD = p —параметр
(перпендикуляр, восставленный в фокусе к большой оси), е — эксцентриситет. Положение планеты М определим в полярных координатах радиусом-вектором
r и полярным углом φ.
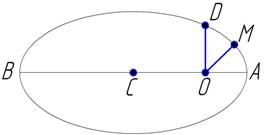
Рис. 35
Если угол φ
отсчитывается от оси ОА по
направлению движения планеты, то уравнение эллипса в полярных координатах имеет
вид
![]() (1)
(1)
Условие постоянства секторной скорости выразится
уравнением
![]() (2)
(2)
где С — постоянная
площадей. Постоянство секторной скорости относительно О означает, что действующая на
планету М сила является центральной,
проходящей через фокус О; ускорение
планеты сводится только к радиальному:
![]() (3)
(3)
Дифференцируя уравнение (1), получаем
![]()
Определив ![]() из уравнения
(2), после подстановки получаем
из уравнения
(2), после подстановки получаем
![]()
Вторая производная имеет вид
![]()
Выражение для ускорения аr принимает вид
![]()
Подставив сюда r
из (1), получаем
![]()
Если масса планеты равна т, то действующая на нее сила
![]() (4)
(4)
Знак минус показывает, что эта сила направлена к
центру и имеет величину, обратно пропорциональную квадрату расстояний от
планеты до Солнца.
Используем теперь третий закон Кеплера: квадраты
времен обращения планет вокруг Солнца пропорциональны кубам средних расстояний,
или, точнее, больших полуосей орбит планет.
Величина С представляет удвоенную секторную скорость. Если а и b
— большие и малые полуоси эллипса, то его площадь равна πаb. Секторную скорость планеты
получим, разделив эту величину на время Т полного обращения; таким образом, ![]()
Как известно из аналитической геометрии, параметр р равняется ![]()
Таким образом,
![]()
Согласно третьему закону Кеплера отношение ![]() для всех планет
постоянно и не зависит от их масс. Тогда
для всех планет
постоянно и не зависит от их масс. Тогда
![]() (5)
(5)
Таким образом, сила притяжения каждой планеты Солнцем
пропорциональна ее массе. Но по третьему закону Ньютона сила, с которой планета
притягивает Солнце, должна, с одной стороны, быть пропорциональна массе Солнца,
а с другой — определяться равенством (5). Если М — масса Солнца, то
![]()
Так как масса Солнца — одна и та же для всех планет,
то выражение ![]() является
постоянной величиной. Обозначив её μ, получим
является
постоянной величиной. Обозначив её μ, получим
![]()
что
выражает закон всемирного тяготения.
Название книги Ньютона «Математические начала
натурально» философии» кажется на первый взгляд необычным. В XVII в. ученые уже
освоили классическую мудрость, где слово «философия», которое переводилось на
русский язык словом «любомудрие». Греческие философы от Фалеса до Аристотеля
подразумевали под философией совокупность всех знаний о природе и человеке; в
нее входили как составные части логика и физика, которая кроме физико- математических наук включала и биологические, а
также этику и эстетику. Из трех книг, составляющих «Математические начала
натуральной философии», основной была последняя, третья книга «О системе мира».
Сам Ньютон писал об этом так: «Я составил об этом предмете третью книгу,
придерживаясь популярного изложения, так чтобы она читалась многими. Но затем,
чтобы те, кто, недостаточно поняв начальные положения, а
потому совершенно не уяснив и силы их следствий и не отбросив привычные им в
продолжение многих лет предрассудки, не вовлек бы дело в пререкания, я
переложил сущность этой книги в ряд предложений по математическому обычаю, так
чтобы они читались лишь теми, кто сперва овладел началами».
Третья книга начинается следующими правилами философствования (Regulae philosophandi):
1. Не следует принимать в природе иных причин сверх
тех, которые истинны и достаточны для объяснения явлений.
2. Поэтому, насколько возможно, необходимо приписывать
те же причины того же рода проявлениям природы.
3. Такие свойства, которые не могут
быть ни усилены, ни ослаблены и которые оказываются присущими всем телам, над
которыми возможно производить испытания, должны быть почитаемы за свойства всех
тел вообще.
Такими свойствами Ньютон считал протяженность,
твердость (по крайней мере атомов), непроницаемость,
подвижность и инерцию. Даже тяжесть он не считал общим свойством, поскольку она
подвержена увеличению или уменьшению с расстоянием.
4. В опытной физике предположения, выведенные из
совершающихся явлений путем индукции, несмотря на возможность противных им
предположений, должны быть почитаемы за верные или в точности, или приближенно,
пока не обнаружатся такие явления которыми они еще
более уточнятся или же окажутся
подверженными исключениям.
После этого Ньютон выписал ряд астрономических данных,
на основании которых он строил свою систему мира при помощи математических
принципов.
Вся первая книга представляет шедевр строго
логического мышления; на основании содержащихся в ней определений и аксиом
можно построить всю механику абсолютно твердых тел.
Назначение второй книги было несколько иным. Ньютону
нужно было не только утвердить свою систему, но и опровергнуть своего соперника
Декарта, объяснявшего движение планет вокруг Солнца при помощи вихрей жидкой
среды, заполняющей космическое пространство; центрами этих вихрей были Солнце,
звезды, планеты и даже их спутники. Эта система предполагала множественность
миров, каждому из которых соответствовал вихрь, образующийся вокруг
центрального тела.
Для опровержения теории Декарта надо было разобраться
в теории движения жидкостей и твердых тел, движущихся в сопротивляющейся среде.
Но эта книга, являющаяся первым трудом в области
гидродинамики, уже не построена так логично, как предыдущая: она не содержит ни
специальных определений, ни аксиом; с чисто полемической точки зрения Ньютону
это не представлялось необходимым. Так как космическое пространство, которое
Ньютон считал пустым, а Декарт — заполненным, находящимся в вихревом движении
веществом, должно представлять сопротивление движущимся в нем телам, то
траектории планет должны иметь вид спиралей, закручивающихся вокруг
центрального тела — Солнца. Рассматривая движение в жидкости цилиндрических
тел, Ньютон даже допустил ошибку, которая была указана только в XIX в. Стоксом.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов