Главная
Тема 23. Конец
великого века
В исторической
жизни человечества бывают сравнительно короткие периоды, в течение которых
происходят резкие, количественные и качественные перемены в общественной и культурной
жизни. Таким периодом был VI век до н. э., когда в Вавилоне было положено
начало вычислительной планетной астрономии, а в Греции появилась философия,
основанная не на религиозных представлениях, а на свободном логическом
мышлении.
Таким же веком
был и XVII век н. э., в начале которого еще сильно чувствовались религиозные
представления со стороны как католиков, так и
протестантов, над мышлением довлели церковные и схоластические авторитеты и
даже образованные люди находились под сильным влиянием мистических учений:
платонизма, астрологии, алхимии и т. д. В течение XVII в. книжные словопрения
сменились экспериментами в лабораториях, расширился горизонт географических
знаний.
Успехи новой
науки ясно видны из развития механики, сделавшейся в это время основным
стержнем научных представлений об окружающем внешнем мире. Источником научного
познания стали наблюдение и опыт, появились исследовательские лаборатории.
В начале XVII в. математическая мысль еще во многих отношениях
развивалась на почве геометрических представлений античной эпохи: властителями
дум были Архимед и Аполлоний Пергский,
работы Архимеда заложили основы интегрального исчисления, которое первоначально
у Галилея и его учеников имело форму метода неделимых и было сильно продвинуто
Паскалем; важную роль сыграла, в частности, уже упоминавшаяся
выше задача о циклоиде.
Для развития
второго отдела математического анализа, а именно дифференциального исчисления,
в работах Архимеда было значительно меньше материалов: для решения вопроса о
проведении касательной к кривой имелась только книга «О спиралях», которая была
переведена учителем Ньютона Исааком Барроу и возможно
послужила толчком к построению так называемого дифференциального треугольника.
С другой
стороны, аналитическая геометрия Декарта и Ферма естественно клонила
математиков к алгебраическим методам решения. Можно указать ряд авторов,
работавших в этом направлении: это был бельгиец Рене-Франсуа Слюз—друг Гюйгенса, один из великих людей, незаслуженно
забытых потомством. До самого недавнего времени он был известен историкам
математики как изобретатель некоторых интересных кривых («слезки» или
«жемчужины» Слюза). Недавно было открыто его
оставшееся ненапечатанным сочинение о проведении» касательных к кривым,
содержащее полную теорию дифференцирования алгебраических функций; почти
несомненно, что рукопись этого сочинения была в руках Лейбница. Следует назвать
и самого Гюйгенса, написавшего для великого пенсионария Яна-де Витта целый
трактат на ту же тему. Однако основная работа в деле создания математического
анализа выпала на долю Ньютона и Лейбница.
В настоящее
время можно считать доказанным, что новый анализ в форме
так называемой теории флюксий был разработан Ньютоном в процессе написания
книги «Математические начала натуральной философии». Хотя эта книга изложена им
в обычной для XVII в. геометрической форме, но это
несомненно было сделано для того, чтобы новое содержание в старой форме стало
приемлемым для читателей; во всяком случае эта книга представляет последнее
большое сочинение по механике, написанное в геометрической форме.
Деятельность
Лейбница в области создания дифференциального исчисления можно проследить по
его переписке с Гюйгенсом. Работы Лейбница в этом направлении начались
несколько позже ньютоновых, а именно в 70-х годах
XVII в. В это время он нашел правило для построения касательной к заданной
кривой, которое бесконечно далеко превосходит известные способы. Гюйгенс
попросил у него пример и Лейбниц послал ему следующую задачу.
Дана кривая,
для которой сумма обратных величин расстояний от ее точек до четырех заданных
точек, лежащих на одной прямой, равна обратному значению длины некоторой
заданной прямой G (рис.36).
Если положить ЕА — s1,
ЕВ = s2, ЕС = s3, ED = s4, то
свойств этой кривой можно выразить уравнением
![]()
Лейбниц указал
и ответ, дав отношение ординаты EF
любой точки этой кривой к отрезку TF
образуемому искомой касательной ЕТ на
оси абсцисс. Полное решение этой задачи было опубликовано Лейбницем в его
основной работе по дифференциальному
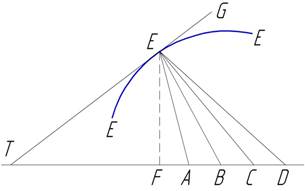
Рис. 36
исчислению
«Новый метод для нахождения максимумов и минимумов, а также касательных», напечатанной в «Acta Eruditorum» за 1684 г.
Выше описаны
достижения, полученные в теоретической механике в результате работ трех
замечательных ученых — Галилея, Гюйгенса и Ньютона. Отметим, что, несмотря на
всю разность социальных положений и национальных
особенностей всех трех людей, в их деятельности есть общие черты: все трое
занимались астрономией, работали в области оптики, добились крупных результатов
в механике и все трое интересовались математикой.
Сравним теперь
творческие характеристики и личную жизнь этих ученых. Галилей — человек
среднего сословия (по положению) в ту эпоху, когда оно только начинало набирать
свои силы. Он стремится познать все до конца; природа представляется для него
совсем несложной; он иногда упрощает свои теоретические построения до такой
степени, что не обращает внимания на получающиеся отсюда неточности. Хорошо знакомый
с Кеплером и его теорией эллиптического движения планет, он все же ни одним
словом не упоминает ее в своих сочинениях: его планетная система по своей
простоте стоит на уровне Аристарха Самосского, признававшего равномерные
круговые движения планет вокруг Солнца.
Галилей очень
ценил математику (известны его слова, что «великая книга природы написана
языком геометрических фигур»)» но все же предпочитал пользоваться ею только
тогда, когда иначе было уже невозможно поступить. В его сочинениях можно найти
большое количество неверных представлений и даже прямых ошибок, но все их
прощаешь за богатство идеи и яркость представлений о природе.
Галилей не был
борцом, отстаивавшим до конца свои идеи; с религией он предпочитал не
связываться, и его «Диалоги о двух системах мира» появились лишь вследствие
ошибочного тактического расчета. Однако
темперамент Галилея в его научных спорах был настолько энергичным, что его
противники оказывались побежденными.
Галилей имел
целую плеяду учеников и последователей, которые оставили после себя яркие (хотя
и недолговечные) следы во время той мрачной феодальной реакции, которая сменила
в XVII в. в Италии блестящую эпоху Возрождения.
Полную
противоположность Галилею представляет Ньютон. В своей жизни, а также и научной
деятельности он, видимо, был самым одиноким человеком нового времени; для него
(по крайней мере, в течение творческого периода его жизни) существовала только
его наука и больше ничего. Хорошо известно его знаменитое «Hypotheses nоn fingo» («Я не придумываю гипотез»); достаточно признать,
что факт существует, и сделать из него необходимые математические выводы.
Ньютон во всем шел до конца: когда для его теории строения Солнечной системы
понадобилась новая математика, он изобретает высший анализ; когда потребовались усовершенствованные телескопы, он создает
новую оптику. Этим он отличается от Галилея и Гюйгенса.
Галилей был
исключительно статичен: не получается — можно подождать; недаром самое важное
его произведение было закончено в конце его жизни.
Что касается
Гюйгенса, то он, наоборот, не довел до конца и даже не дописал большинства
своих произведений; даже основная тема его жизни — создание хронометра,
пригодного для морских путешествий, — была решена только после его смерти —
правда, на основании его принципов. В этом отношении кроме его необычной
требовательности ему мешала й обстановка, в которой протекала его жизнь в
Голландии.
Позднее, когда
он работал во Франции в Парижской Академии (к будущности которой, нужно
сказать, он относился весьма скептически), общественные отношения,
необходимость научных демонстраций высокопоставленным людям отнимали у него
очень много времени.
Идущий до
конца в своих научных работах, Ньютон был религиозным человеком вроде тех
пуритан, которые сделали английскую революцию 40-годов XVII в. и оказались не у
дел во время реставрации Стюартов, а также в период правления сменивших их
Оранской и Ганноверской династий. Эта религиозность Ньютона выразилась и в его
произведениях последнего периода его жизни («Толкования на Апокалипсис и на
пророчества Даниила»), и даже в его строго научных произведениях.
Гюйгенс,
стоящий хронологически посредине между Галилеем и Ньютоном, занимает между ними
среднее место и по многим чертам своего характера. В нем нет ни «буйной жизнерадостности
Галилея, ни сумрачного одиночества» Ньютона.
Гюйгенс как
дворянин был обучен всем хорошим манерам, в том числе сдержанности и учтивости.
Кроме отца и братьев — Константина и Лодевика — Гюйгенс больших друзей,
по-видимому, не имел, хотя у него было громадное количество знакомых, причем
близости мешало не только чувство сословного превосходства.
В семье своего
отца Гюйгенс получил блестящее образование: он знал греческий, латинский,
французский, итальянский, испанский и английский языки. Его переписка велась
главным образом на латинском языке — с учеными — и на французском — с братьями
и хорошо знакомыми; на голландском языке он писал официальные донесения Штатам,
инструкций по кораблевождению и полировке стекол и письма своей сестре Сюзанне,
да и то до тех пор, пока она не научилась французскому языку. Кроме того,
Гюйгенс очень хорошо рисовал, великолепно знал музыку и разбирался в
архитектуре и живописи. Он хорошо знал произведения классических авторов Греции
и Рима, а также итальянского Возрождения и доминировавшей в его время испанской
литературы (Кальдерона, Лопе де Вега); из французских авторов он ценил Корнеля,
Мольера, Расина.
Дух
классицизма был очень силен у Гюйгенса; может быть этим даже
объясняется и то предпочтение, которое он оказывал греческой геометрии
перед арабской алгеброй.
Получивший
классическое образование и светски воспитанный человек, Гюйгенс занимался
физическими работами, полировал оптические стекла, конструировал телескопы,
микроскопы, воздушные насосы и даже планетарий по примеру Архимеда, имел дела с
часовыми мастерами и прилагал все усилия, чтобы штурманы купеческих кораблей в
своих путешествиях в колонии имели надежные средства для определения своего
местонахождения.
Связь с
практикой у Гюйгенса проявляется даже в математике. Он стремится к полной
строгости своих доказательств, неоднократно их переделывает, но вместе с тем
математика только для математики для него не существует.
Ньютон мое
среди своих занятий уделить время чисто математическому исследованию кривых
третьего порядка; для Гюйгенса подобное предприятие было совершенно немыслимым.
Единственный раз он увлекся чистой математикой, когда занялся исследованиям
теории игр, да и здесь на него повлияли его парижские ученые, для которых этот
вопрос имел существенное значение.
В области
физики Гюйгенс тоже занимает среднее место между Галилеем и Ньютоном. У Галилея
гипотезы о физической природе явлений занимают много места и не все они
правильны; Ньютон вообще никаких «гипотез не выдумывал»; у Гюйгенса они есть,
но занимают довольно скромное место, и, если исключить его теории тяготения,
они почти все перешли в золотой фонд позднейшей физики.
То же самое
можно сказать об его отношении к природе. Для Галилея она была источником
наслаждения, для Ньютона — предметом изучения. Гюйгенс воспринимал природу
через призму искусства или науки.
Такое же
отношение характерно и для национальной литературы. Если Галилея можно считать
одним из родоначальников итальянской прозы (за свои коперниканские воззрения он
пострадал отчасти потому, что «Диалоги о двух важнейших системах мира» были
написаны по-итальянски), то Гюйгенс меньше всего писал на родном голландском
языке.
Одна черта
мировоззрения Гюйгенса очень сильно выделяла его среди людей XVII в. Все три великих современника — Декарт, Галилей, Ньютон —
были по-своему, один больше, другой меньше, религиозными. Про Гюйгенса этого
сказать уже нельзя. Известное значение, вероятно, имело то обстоятельство, что
юность Гюйгенса протекала в эпоху Тридцатилетней войны (1618—1648). Тридцатилетнюю
войну называют «школой европейского вольномыслия». В этой школе молодой Гюйгенс
оказался хорошим учеником. Когда в 1660 г. иезуитский математик патер Такэ
попытался совратить его в католицизм, то Гюйгенс написал ему, что все это
далеко отстоит от очевидности геометрических доказательств.
Посмертные
победы Гюйгенса — признание волновой теории света в XIX в., критика ньютоновой
механики, приведшая к созданию принципа относительности в
начале XX в., — оказали большое влияние на дальнейшее развитие
теоретической механики. В жизни Гюйгенса были два момента, которые представляют
несомненный интерес для науки начала XX в., — покорение воздушного пространства
и космические полеты.
Воздухоплавание
стало возможным только после создания достаточно легкого двигателя, а именно
двигателя внутреннего сгорания. Первый такой двигатель был создан Гюйгенсом в
1673 г. В составленной им для Парижской Академии программе исследований стояли
два пункта: «Исследовать силу, заключенную в орудийном порохе, помещая его в небольшом
количестве в железный или медный ящик достаточной толщины; таким же образом
исследовать силу воды, разреженной огнем». Последнюю идею, он, по-видимому,
заимствовал у Паскаля, с которым говорил на эту тему в 1660 г. во время
путешествия по Франции. Эта тема, приведшая к
изобретению парового двигателя, была разработана Денисов Папеном, бывшим
сотрудником Гюйгенса по его работе в Академии; первую же он разрешил сам,
построив прибор, где при помощи взрыва пороха можно было получить силу,
поднимающую груз. Он считал возможным подняться в воздух не при помощи
«легкости» пустоты, а под действием силы движения, приложенного к крыльям или к
чему-либо подобному.
Первый
действующий по этому принципу двигатель был построен в 1867 г. (двухтактный
газовый двигатель), но только вместо пороха был применен светильный газ.
Вторая точка
соприкосновения Гюйгенса с современностью заключается в последнем его
произведении «Cosmotheoros» («Мирозритель»), посвященном жизни на других
планетах. Тема межпланетных путешествий встречалась еще в древности. Строго говоря это была запретная тема, пожалуй, даже более опасная,
чем теория Коперника. Интересно отметить, что теория Коперника на Руси не
преследовалась: первое упоминание о ней находится в пере, воде «Селенографии»
польского астронома Гевелия. В этом переводе система Коперника трактуется как
равная птолемеевой.
Вопрос об
обитаемости планет у Гюйгенса рассматривался с научно допустимой точки зрения
относительно возможных на них физических условий. Особенно много внимания Гюйгенс
уделил рассмотрению того, как могут представляться движения других планет
жителям какой-либо одной из них. Самая последняя запись в его
рукописи, относящаяся к концу 1694 г. или началу 1695 г., содержит вычисления
наибольших элонгации Меркурия от Солнца, наблюдаемых с различных планет,
начиная от Венеры и кончая Сатурном.
В 1717 г. по
указанию Петра I эта книга была переведена на русский язык.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов