Главная
Тема 28. Жозеф
Луи-Лагранж. Принцип возможных перемещений. Основания аналитической механики
Три великих имени характеризуют развитие механики в
XVIII в.: Ньютон создал систему классической динамики, Эйлер выразил ее в
математической форме, Лагранж подвел все итоги развитию механики XVIII в. и
создал произведение, которое стало определяющим для теоретической механики
первой половины XIX в.
Жозеф-Луи Лагранж (1736—1813) родился в Турине — столице Сардинского
королевства, на долю которого в Х1Х в. выпала роль объединителя Италии. Он не
мог похвалиться знатностью рода; его отец, служивший
военным казначеем, разорился, и Лагранжу приходилось пробивать себе дорогу
собственными силами. Его математические способности были замечены, и он работал
в качестве преподавателя в одном из военных училищ Турина, но в возрасте 30 лет
покинул родину.
В 1759 г. он стал членом Берлинской Академии наук, в
1766 г. переехал в Берлин и занял пост президента физико-математического
отделения после Эйлера, продолжателем которого он и является. Его можно было бы
назвать скорее математиком, чем механиком, но в XVIII в. еще не произошло
дифференциации между этими науками.
В развитии механики появление
«Аналитической механики» Лагранжа было выдающимся событием. В 1813-1815 гг.
этот труд вышел вторым, дополненным изданием и с тех пор
несколько раз в течение XIX
столетия переиздавался с дополнениями и примечаниями других ученых.
Русский перевод в двух томах появился в 1950 г.
Жозефу Лагранжу принадлежат
многие выдающиеся работы по механике. С его именем до первого издания
«Аналитической механики» связаны исследования о задаче трех тел, о применении в
механике принципа наименьшего действия, о задаче вращения твердого тела вокруг
неподвижной точки («гироскоп Лагранжа»), по теории волн на поверхности жидкости
и др.
Как в этот период, так и
после первого издания своего трактата Лагранж занимался небесной механикой и
получил в этой области немало важных результатов: по расчету орбит планет и
комет, по общим методам решения уравнений, определяющих движение тел Солнечной
системы. В «Аналитическую механику» включены многие замечательные достижения
Лагранжа, но она вошла бы в историю науки даже без них, благодаря
оригинальности системы изложения и единству метода, использованного ее автором.
В предисловии к первому изданию Лагранж с полным основанием писал, что
«существует уже много трактатов по механике, но план настоящего трактата
является совершенно новым. Я поставил себе целью свести теорию механики и
методы решения связанных с нею задач к общим формулам,
простое развитие которых дает все уравнения, необходимые для решения каждой
задачи». И с законным удовлетворением Лагранж добавил к этому: «Я надеюсь, что
способ, каким я постарался этого достичь, не оставляет желать чего-либо
лучшего». Поэтому особенно поучительно познакомиться с тем, на основе каких
исходных положений и какими средствами Лагранж создал стройную систему своей
(аналитической) механики.
В предисловии к «Аналитической механике» он писал о
том, что цель создания этой книги — свести теорию механики и методы решения связанных с нею задач к общим формулам, простое
развитие которых дает все уравнения, необходимые для решения каждой задачи.
Сам Лагранж характеризовал
свои методы таким образом: они «не требуют ни построений, ни геометрических или
механических рассуждений; они требуют только алгебраических операций,
подчиненных планомерному и однообразному ходу. Все, любящие анализ (подразумевается
математический анализ, анализ бесконечно малых.), с удовольствием убедятся в
том, что механика становится новой отраслью анализа, и будут мне благодарны за
то, что этим путем я расширил область его применения». Эта характеристика, если
принять ее безоговорочно, означает, что аналитическая механика Лагранжа
является ветвью анализа, что она механика, лишенная «механических рассуждений»,
так как в ней указаны общие методы для составления уравнений любой задачи
механики, после чего решение становится чисто математической проблемой.
Он сознательно не дает чертежей в своей книге даже
там, где они имели бы существенное значение в понимании вопроса (например, в
его доказательстве принципа возможных перемещений при помощи полиспастов).
Излагаемые им методы не требуют ни построений, ни геометрических или
механических рассуждений; они требуют только алгебраических операций,
подчиненных планомерному и однообразному ходу. Все любящие анализ с
удовольствием убедятся в том, что механика становится новой отраслью анализа.
После «Аналитической механики», вышедшей в 1788 г., он
написал книгу «Теория аналитических функций» (1797) и связанные с ней «Лекции
по исчислению функций» («Leсons
sur le calcul
des Fonctions»), вышедшие в
1801 г., а затем «Решение числовых уравнений» (1798).
Если Гюйгенс считал теорию чисел «не заслуживающей
внимания», а Эйлер касался ее лишь мимоходом, то Лагранж посвятил ей ряд
мемуаров, в частности о решении в целых числах неопределенных уравнений второй
степени. Его исследования в области прикладных наук касаются
или движения твердого тела (первый мемуар в 1773 г.),
или же астрономии, занятия которой были как бы обязательными для каждого
механика XVIII в.; ей он также посвятил ряд мемуаров, напечатанных в Берлинской
и Парижской Академиях; наиболее замечательным является мемуар
о задаче трех тел (1772).
Иногда Лагранжа представляют кабинетным
ученым-математиком, далеким от каких-нибудь практических задач. Такое
представление о Лагранже нельзя назвать правильным. Во время
революции 1789—1794 гг. он участвовал в создании Политехнической школы, в
работах по установлению метрической системы, и Конвент, издавший декрет об
удалении из Франции всех иностранцев, сделал исключение для Лагранжа, хотя он
родился вне Франции и переехал в Париж только в 1788 г. В 1794—1795 гг. он
читал лекции по арифметике и алгебре для учеников Нормальной школы
(подготовительной к Политехнической), а в следующем
году участвовал в «Собрании различных сочинений по политической арифметике».
Основным произведением Лагранжа является его
«Аналитическая механика», которую он разделяет на две части: статику и
динамику; это первое произведение, в котором объединяются оба эти отдела
механики, разрабатывавшиеся до этого времени независимо один от другого. В
главе «Статика» Лагранж ставит общий принцип, называемый им «принцип
виртуальных скоростей», в настоящее время «принцип возможных, или виртуальных,
перемещений». Вот какое определение Лагранж дает статике: статика есть наука о
равновесии сил. Вообще под силой (force), или
потенцией (puissance), подразумевают
какую бы то ни было причину, сообщающую или стремящуюся сообщить
движение телу, к которому она предполагается быть приложенной; и этим
количеством движения, сообщенного, или готового быть сообщенным, и следует
оценивать силу, или потенцию.
В дальнейшем Лагранж оба термина для обозначения силы
употребляет почти одинаково; самое большее, что можно заметить, это то, что
потенцией он чаще называет движущую силу. Затем, характеризуя силу количеством
движения, он сближает обычные силы с ударными (для обозначения которых он
употребляет термин «импульс»); термина «ускорение» Лагранж не знает; он
пользуется ньютоновым термином «ускоряющая сила»,
понимая под этим силу, деленную на массу, или силу, действующую на единицу
массы. Это определение силы через скорость чувствуется и в самом названий
принципа «виртуальная скорость», хотя в доказательстве его Лагранж употребляет
не термин «скорость», а термин «перемещение».
Изданием в 1736 г. «Механики»
Эйлер заложил основы аналитической механики, которой затем много занимались он
сам, Клеро, Даламбер, Д. Бернулли и другие ученые XVIII в. Но у Эйлера задачи механики хотя и
решаются средствами анализа бесконечно малых, однако каждая сводится к решению
уравнений по-своему. Кроме того сочинение Эйлера 1736 г. – это механика
материальной точки. В своих дальнейших трудах, как мы уже знаем, Эйлер и другие
ученые развили динамику твердого тела. Лагранж охватил механику системы
материальных точек и тел и создал единообразный и общий метод сведения
механических задач к решению соответствующих математических задач. Но ясно, что
при этом ему приходилось исходить из каких-то физических, экспериментальных
положений. Каковы эти положения? И насколько общими являются методы Лагранжа,
действительно ли они охватывают все задачи механики?
Ответы на эти вопросы
познакомят нас с тем, что действительно можно назвать механикой Лагранжа. Эта
механика делится на две части: статику и динамику. Статика у Лагранжа основана
на принципе виртуальных (возможных) скоростей. «Под виртуальной скоростью
следует понимать скорость, которую тело, находящееся в равновесии, готово
принять в тог момент, когда
равновесие нарушено, т. е. ту скорость, какую тело фактически получило бы в
первое мгновение своего движения». Принцип виртуальных скоростей формулируется
так: «Если какая-либо система любого числа тел, или точек, на
каждую из которых действуют любые силы, находится в равновесии и если этой
системе сообщить любое малое движение, в результате которого каждая точка
пройдет бесконечно малый путь, представляющий ее виртуальную скорость, то сумма
сил, помноженных каждая соответственно на путь, проходимый по направлению силы
точкой, в которой она приложена, будет всегда равна нулю, если малые
пути, проходимые в направлении сил, считать положительными, а проходимые в
противоположном направлении считать отрицательными».
Вводя этот принцип, Лагранж
ссылался на данные опыта. Он указывал на общий закон равновесия машин:
отношение сил друг к другу обратно отношению скоростей точек, к которым они
приложены, причем скорости должны измеряться в направлении сил. Это положение,
взятое в общем виде, и составляет принцип виртуальных скоростей, который «можно
рассматривать как своего рода аксиому механики». Впрочем, Лагранж дал и два
доказательства принципа виртуальных скоростей, но, разумеется, эти
доказательства состоят в том, что этот принцип сводится к другим положениям
статики. Наиболее известно доказательство, приведенное во втором издании
«Аналитической механики». Оно основано на «принципе блоков». Считая последний
принцип вполне наглядным, Лагранж рассматривал его как естественное основание
для принципа виртуальных скоростей.
В динамике Лагранж исходит из
двух законов: закона инерции и закона сложения движений (по правилу
параллелограмма). Второй закон механики Ньютона Лагранж как бы выводит из этих
двух следующим образом. В равномерно ускоренном движении существует постоянное
отношение между скоростями и временами. Это отношение принимается за меру
ускоряющей силы, непрерывно действующей на тело, - ведь эта сила может быть
измерена только по такому ее действию. В общем же случае, «каковы бы ни были
движение тела и закон его ускорения, но, согласно природе дифференциального
исчисления, мы можем признать постоянным действие каждой ускоряющей силы в
течение бесконечно малого времени, таким образом
всегда можно определить величину силы, действующей на тело в любое мгновение,
если вызванную в это мгновение скорость сравнить с продолжительностью этого
мгновения...». Эту схему перехода от равномерно ускоренного движения (Галилей)
к общему случаю Лагранж связывает с именем Гюйгенса, построившего теорию
центробежных сил. Ньютон, по Лагранжу, обобщил эту теорию Гюйгенса на все
кривые линии и тем дополнил учение о неравномерных движениях и об ускоряющих
силах, способных их вызвать. Сам Ньютон постоянно пользовался геометрическим
методом, но «в настоящее время это учение сводится лишь к нескольким очень
простым дифференциальным формулам».
Аналитическая динамика
Лагранжа основана на общей формуле, которую сейчас называют уравнением
Даламбера – Лагранжа или общим уравнением динамики. «Развитие этой формулы,
если при этом принять во внимание условия, зависящие от природы системы, дает
все уравнения, необходимые для определения движения каждого тела, после этого
остается только эти уравнения интегрировать, что является уже задачей анализа».
Исходя из своего общего
уравнения динамики, Лагранж вывел дифференциальные уравнения движения в двух
видах, соответствующих двум видам уравнений статики. Это знаменитые уравнения
движения Лагранжа первого и второго рода. Уравнения движения второго рода
замечательны тем, что для систем, при движении которых не изменяется их полная
механическая энергия (консервативные системы), эти уравнения можно составить,
зная общее выражение только двух величин: кинетической энергии системы и ее
потенциальной энергии. Число этих уравнений минимально, оно равно числу
степеней свободы системы. Вместе с тем уравнения Лагранжа весьма общи: их можно
использовать для разных физических систем, если состояние таких систем характеризуется
значениями их кинетической и потенциальной энергии. Кроме того, уравнения
движения в форме Лагранжа второго рода имеют определенную структуру с
математической точки зрения. Поэтому задача их решения (интегрирование) в общем
виде является достаточно определенной, чтобы исследовать ее чисто
математически. Знаменитый физик Максвелл имел все основания писать в своем
«Трактате об электричестве и магнетизме», касаясь значения «Аналитической
механики» Лагранжа:
«Так как благодаря созданию
математической теории динамики развитие идей и методов чистой математики
сделало возможным выявление многих истин, которые нельзя было бы открыть, не
обучившись математике, то, если мы хотим создать динамическую теорию других
наук, мы должны воспринять и эти динамические истины, и математические методы.
Формулируя
идеи и термины любой науки, имеющей дело, как паука об электричестве, с силами
и с их действиями, мы должны постоянно иметь в виду идеи, являющиеся достоянием
основной пауки – динамики, чтобы мы могли с самого начала развития пауки
избежать противоречий с тем, что уже установлено, а также для того, чтобы с
уточнением наших взглядов принятый нами язык нам помогал, а не мешал».
Принципом наименьшего
действия Лагранж много занимался в первые годы своей научной деятельности в
связи с работами по вариационному исчислению. При систематическом изложении
механики этот принцип отходит у Лагранжа на второй план. Все же существенно
было то, что Лагранж формулировал этот принцип с полной определенностью как
чисто механическую теорему, справедливую при соблюдении определенных условий. Эта формулировка такова: при движении любой системы тел,
находящихся под действием взаимных сил притяжения или сил, направленных к
неподвижным центрам и пропорциональных каким-либо функциям расстояний, кривые,
описываемые различными телами, а равно их скорости необходимо таковы, что сумма
произведений отдельных масс на интеграл скорости, умноженной на элемент кривой,
является максимумом или минимумом – при условии, что первые и последние точки
каждой кривой рассматриваются как заданные.
Эта формулировка, как видим,
приводит к уже знакомой нам записи: обращается в нуль вариация суммы величин
вида
где m – масса одной из точек системы, v – ее скорость, ds – элемент пути, или, иначе говоря,
бесконечно малый отрезок траектории точки т. К этому Лагранж добавляет,
что ds = vdt (dt обозначает тот бесконечно малый промежуток
времени, в течение которого точка m проходит путь ds), поэтому
вместо 
можно написать 
или 
. Тут под знаком интеграла мы видим
(удвоенную) живую силу
точки, а так как нам надо взять сумму таких величин для всей рассматриваемой
механической системы, то в итоге под знаком интеграла окажется (удвоенная)
живая сила всей системы в любое мгновение. Таким образом, говорит Лагранж,
рассматриваемый принцип сводится собственно к тому, что сумма живых сил всех
тел от момента, когда они выходят из заданных точек, до того момента, когда они
приходят в другие заданные точки, является максимумом или минимумом.
Следовательно, этот принцип можно было бы с большим основанием назвать
принципом наибольшей или наименьшей живой силы.
По мнению Лагранжа, такая
формулировка имела бы то преимущество, что она была бы общей как для движения,
так и для равновесия, поскольку в статике Лагранж доказывал, что при
прохождении положения равновесия живая сила системы бывает наибольшей или
наименьшей.
Формулировку своего принципа Лагранж
дает в таких выражениях: если на какую-либо систему тел или точек действуют
какие-либо потенции и эта система находится в равновесии и если этой системе
сообщить какое-либо малое движение, в результате которого каждая точка пройдет
бесконечно малое пространство, то сумма потенций, умноженных каждая на
пространство, которое точка ее приложения проходит по направлению этой самой
потенций, всегда равна нулю, если
считать положительными малые пути, проходимые в
направлении силы, а отрицательными — проходимые в противоположном направлении.
Доказательство этого принципа Лагранж производит
заменяв каждую силу (потенцию) полиспастом АВ,
где А — неподвижна обойма, а В — подвижная, представляющая собой
точку приложения силы (рис. 37); направление силы определяется
последовательностью от А к В, а величина — числом оборотов нитей,
проходящих в полиспасте от А к В.
Пусть точки В1, В2, В3 — точки
приложения сил Р1, Р2,
Р3, а А1, А2,
A3 — неподвижные обоймы соответствующих полиспастов. В точка A1 закрепляется гибкая нить,
которая проходит через B1
и после n1 оборотов идет к
A1 и А2; затем через n2, оборотов через В2 возвращается к А2, идет к A3 и через п3 оборотов возвращается к A3,
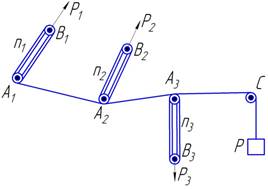
Рис. 37
откуда
через неподвижный блок С опускается
вниз, имея на конце груз Р,
представляющий общую меру всех сил Р1,
Р2, Р3:
Точкам В1, В2,
В3 Даем перемещения, проекции которых на
направления полиспастов соответственно α1, α2,
α3. Если вся система находится в равновесии, то остается
неподвижной и точка C приложения
груза Р.
Поскольку нить нерастяжима, то алгебраическая сумма всех ее удлинений равна
нулю:
откуда
после умножения этого равенства на Р получаем:
что
и доказывает формулируемый принцип.
В общем случае, если приложенные силы Р, Q, R,..., а длины полиспастов р, q, r, ..., то бесконечно малые
перемещения α1, α2, α3,...
выразятся через дифференциалы и формула Лагранжа получает вид
Каждый член этой формулы, например Pdp, Лагранж называет моментом силы Р9 принимая термин «момент» в том смысле, который дает ему
Галилей, т. е. как произведение силы на ее виртуальную скорость. /
В настоящее время можно поставить вопрос: является ли
принцип возможных перемещений не требующим доказательства, чем-то вроде новой
аксиомы, или же его можно свести к более первоначальным
принципам, например к трем аксиомам Ньютона? Попробуем это сделать с той
точностью, которая требуется сейчас.
Так как любую механическую систему можно рассматривать
как совокупность материальных точек, то достаточно ограничиться лишь тем, что
будем считать доказанными все теоремы, касающиеся материальной точки; для этого
понадобится лишь определение элементарной работы и теорема кинетической
энергии.
Прежде всего нужно выяснить,
что подразумевается под равновесием системы материальных точек или тел и, в
частности, каково различие между двумя терминами «равновесие» и «покой».
В геометрической статике рассматривают равновесие сил
и равновесие тела. Под равновесием сил, приложенных к твердому телу,
подразумевается случай, когда совокупность этих сил образует систему,
эквивалентную нулю.
Рассматривать равновесие сил, приложенных к различным телам,
в самом общем случае не имеет физического смысла. Если силы, приложенные к
одному твердому телу, находятся в равновесии, то тело может находиться в покое
или же совершать инерционное, т. е. прямолинейное поступательное и равномерное,
движение.
В аналитической статике различие между покоем и
равновесием устанавливается так. Считают, что система материальных точек
находится в покое, если можно найти такую инерциальную систему отсчета, для
которой скорости всех ее точек в данный момент или в течение некоторого
промежутка времени равны нулю.
Отметим, что это определение не исключает «мгновенного
покоя», когда скорости всех точек системы равны нулю только в данный момент
времени (например, брошенное вверх тело будет находиться в покое, когда оно
достигнет наибольшей высоты). Равновесия в данном случае нет, так как ускорения
точек тела в этот момент не равны нулю.
Равновесие может наблюдаться только в течение
некоторого сколь угодно малого, но не равного нулю, промежутка времени; его
определение кроме равенства нулю скоростей требует и равенства нулю ускорений;
скорости точек тела должны не только быть, но и оставаться равными нулю. Это
требует предположения равенства нулю в рассматриваемый момент также и
ускорений.
В геометрической статике при помощи аксиомы связей
можно решать задачи на равновесие тела, когда оно считается свободным.
При пользовании методом Лагранжа это не является
необходимым. Наложенные на точку связи могут выражаться уравнениями или
неравенствами, которым должны удовлетворять координате этой точки (или вообще
точек системы); если в уравнения этих связей время явно не входит, т. е. связи
не изменяются с течением времени, то связи называются склерономными, в
противном случае они являются реономными. И в том и в другом случае такие связи
называются голономными или целочисленными. Может случиться, что связи
налагаются также и на скорости различных точек и не могут быть выражены
уравнениями, содержащими только координаты: такие связи называются
неголономными. Во времена Лагранжа такие связи не употреблялись, но
представление о них он имел.
Понятие о связях соединено с понятием о возможных
перемещениях; возможными называем перемещения, которые допускают связи в
рассматриваемый момент. Если уравнение связи имеет вид f (x, y, z, t) = 0, то возможное перемещение должно удовлетворять
уравнению
Время t в
данном случае остается постоянным. Действительными называются перемещения dx, происходящие в некоторый, хотя бы
бесконечно малый, промежуток времени dt;
они удовлетворяют уравнению
Возможные перемещения обозначают δ—вариации, действительные d — дифференциалы. Возможные перемещения
могут зависеть от времени (возможное сегодня может оказаться невозможным завтра),
но для каждого момента времени их может существовать бесконечно большое
количество. Действительное перемещение, совершающееся между моментами t и t
+ dt, для промежутка времени dt
может быть только одно. Возникает вопрос: будет ли среди возможных перемещений δх, δу, δz находиться и
действительное? Вид уравнений (1) и (2) показывает, что это может быть только в
том случае, когда, 
, т. е. если связи склерономные.
Таким образом, действительное перемещение может и не
оказаться среди возможных. Это кажется парадоксальным,
так как все естественные процессы подчиняются законам природы, которые
считаются постоянными, во всяком случае в некоторой
области пространства и в некоторый промежуток времени. Но эти законы можно
рассматривать тоже как некоторые связи, причем эти связи следует считать
склерономными.
Если рассчитывать положения планет две тысячи лет тому
назад, то надо предполагать, что в то время планетные законы были такими же,
как и в тот момент, когда эти расчеты производятся.
Пусть
L
= 0; M = 0; N = 0, ...
различные
уравнения между координатами точек системы (считаем, что время t в них не
входит). В таком случае возможные перемещения получим
продифференцировав эти уравнения. Они удовлетворят условиям
По Лагранжу, с помощью уравнений
будем
выражать условные уравнения между этими дифференциалами, независимо от того,
являются ли эти уравнения сами по себе полными дифференциалами или же нет при
условии, что дифференциалы только линейные.
Случай, когда dL...
имеют вид
и
т. д., и не представляют полного дифференциала, т. е. не могут быть
проинтегрированы, как раз и характеризует неголономные связи.
Введем еще одно определение. Если условие голономной
связи выражается уравнением L= 0, то
связь называется неосвобождающей, а возможные перемещения — двусторонними,
иными словами, если возможно перемещение δr,
то будет возможным и перемещение — δr.
Если же эти условия выражаются неравенствами L≥0, то связи называют
освобождающими, а перемещения — односторонними; точка может покинуть связь L =
0 только в том направлении, где L может иметь положительные величины, но
не наоборот.
Теперь в формулированное выше Лагранжем выражение
принципа введем следующие дополнения:
1) система отсчета должна быть инерциальной;
2) связи не должны зависеть от времени;
3) сумма элементарных работ на возможных перемещениях
должна быть или равна нулю (связи неосвобождающие), или меньше нуля (связи
освобождающие).
Выраженное условие должно быть и необходимым и
достаточным.
Необходимость условия доказывается следующим образом.
Прежде всего, если хотя бы одна из точек движется, то, согласно определению,
равновесия нет. Поэтому можно лишь предположить, что в некоторый момент все
точки системы находятся в покое. Докажем, что эта система остается в покое. Так как связи не зависят от времени, то в числе возможных
перемещений находятся и действительные; сообщим их системе; если сумма
элементарных работ при этом перемещении больше нуля, то, согласно теореме о
кинетической энергии, система получает некоторую кинетическую энергию; иными
словами, если хоть одна из точек системы обладает скоростью, то равновесие
невозможно.
Достаточность условия доказывается так. Предположим, что
в некоторый момент времени все точки находятся в покое, т. е. кинетическая
энергия системы равна нулю. Если теперь при всех возможных перемещениях, в
числе которых есть и действительные, сумма элементарных работ равна нулю или
меньше нуля, то кинетическая энергия системы или остается такой же, или
уменьшается. Но так как кинетическая энергия не может быть меньше нуля, то
последний случай исключается; следовательно, равная нулю в начальный момент
кинетическая энергия остается такой же и в последующие моменты, т. е.
наблюдается состояние равновесия.
После этого рассматриваются методы вычисления
виртуальных моментов Pdp. Лагранж
указывает, что Р
может быть не только «линией» (т. е. длиной), но и вообще какой угодно
величиной. Таким образом, вводится понятие об обобщенной координате и
соответственно этому об обобщенной силе. Это представляет новый и очень
существенный этап развития механики, который в полной мере был оценен только во
второй половине XIX в.
Лагранжева обобщенная сила может быть чем угодно — силой,
вращающим моментом и т. д., но только не векторной величиной. Введение
обобщенных координат позволяет составлять уравнения равновесия материальной
системы, не расчленяя ее на части. Обобщенная координата представляет параметр,
определяющий положение рассматриваемой системы. Если связи голономны, то число
степеней свободы равно числу независимых параметров (координат), определяющих
положение системы; в общем случае число степеней свободы определяется как число
независимых перемещений, которые может иметь эта система.
В «Статике» Лагранж выводит шесть уравнений равновесия
свободного твердого тела и рассматривает свойства равновесия, относящиеся к
«максимуму» и «минимуму», и в частности случай, когда выражение
оказывается
полным дифференциалом некоторой функции координат p, q, r.... Эта функция обозначена П. Позже она
получила название силовой, или потенциальной, функции. При ее наличии
отыскание положений равновесия системы сводится к определению максимумов и
минимумов функции П. Случаи максимума
и минимума Лагранж связывает с понятием об устойчивости равновесия; в
современной форме минимум потенциальной энергии соответствует устойчивому, а
максимум — неустойчивому положению равновесия.
Лагранж рассматривает также метод неопределенных
множителей. Если р, q, r — обобщенные координаты, то
уравнение Лагранжа имеет вид
(1)
В случае свободной системы получаем уравнение
равновесия, приравнивая к нулю коэффициенты при δp, δq,... . Если на систему наложены связи, уравнения
которых
, (a)
то
уравнения равновесия можно получить помножив полные
дифференциалы в левых частях этих уравнений на неопределенные множители λ,
μ, ν и прибавив их к (1).
Решение задачи сведем к нахождению корней системы
уравнений:
……………………………
Число этих корней равно числу обобщенных координат p, q, r, к которому присоединяется число
уравнений (а). Лагранж показывает, что член λδL
можно рассматривать как «момент» некоторой силы λ, стремящейся изменить
значение функции L. Таким образом,
метод неопределенных множителей позволяет кроме положений равновесия системы
определить также и сопротивления связей (реакции), выражаемых уравнениями (а).
В «Статике» Лагранж выводит также уравнения равновесия
гибкой нити и условия равновесия идеальной жидкости.
Отметим, что обобщенные силы у Лагранжа не являются
векторами, поэтому вопросы приведения систем к простейшему виду полностью
выпадают из рассмотрения. Связи у Лагранжа являются связями идеальными. Поэтому
совершенно естественно, что на практике к изложению Лагранжа пришлось добавить
большое количество материала весьма разнородного качества: произошло разделение
механики на теоретическую и техническую.
Принцип виртуальных скоростей Лагранжа был создан не в
1788 г., когда вышла «Аналитическая механика». Первое упоминание о нем
встречается в мемуаре о либрации Луны (1764 г.), помещенном в трудах Парижской
Академии.
Перейдем к рассмотрению динамики Лагранжа. Обычно
считается, что вся она выросла из так называемого всеобщего уравнения механики,
или принципа Д'Аламбера в форме Лагранжа,
Лагранж пользуется вместе с Ньютоном и Эйлером
понятием об ускоряющих силах (силах, действующих на единицу массы), которые у
него выражаются вторыми производными 
для различных координатных осей. Каждое тело т системы
можно рассматривать как находящееся под действием подобных сил; следовательно,
все эти силы должны быть эквивалентны тем, под влиянием которых, согласно
допущению, находится система, и действие которых видоизменяется вследствие
природы самой системы.
Поэтому он сравнивает выражения: момент ускоряющих сил
и
момент действующих сил
Этот момент Лагранж берет со знаком минус, поскольку,
согласно его условиям, силы Р, Q, R, …
стремятся уменьшить линии р, q, r,...,
представляющие собой расстояния от точек систем до центров сил, к которым
направлены силы, приложенные к материальным точкам системы *.
Таким образом, основное уравнение динамики Лагранж
приводит в виде
Из этого уравнения Лагранж выводит три основные
теоремы динамики, или, как их называли в то время, принципы движения центра
тяжести, площадей и живой[ силы.
В «Динамике» Лагранж вводит динамические уравнения
первого и второго рода. Уравнения первого рода не представляют интереса: они
приводятся в декартовых координатах с такими же неопределенными множителями,
как уравнения равновесия в статике. Но уравнение второго рода следует
рассмотреть.
Лагранж исходит из общего уравнения динамики, которое
приведем без сумм:
Вводим обобщенные координаты:
Действующие силы X,
Y,..., выражейые через q
принимают вид Q(q). Тогда исходное
уравнение
приведем
в виде
(а)
В правой части стоит сумма работ обобщенных сил; левая
часть имеет размерность кинетической энергии; попробуем выразить ее через кинетическую
энергию 
Постараемся освободиться от производных второго
порядка. Левую часть выразим по известной формуле
Тогда
Согласно основной лемме вариационного исчисления,
производная от вариации δх равна
вариации от производной δх.
После этого второе слагаемое принимает вид
Первое слагаемое преобразуем так, чтобы в нем тоже
получилась частная производная от величины Т:
Возьмем частную производную от х по обобщенной скорости q:
Таким образом, первое слагаемое получает вид
и уравнение (а) в окончательном виде
представит уравнение Лагранжа второго рода.
Эти уравнения имеют многочисленные приложения; Лагранж
использовал их при установлении теории малых колебаний около положения
устойчивого равновесия.
Для изучения колебаний с двумя и более переменными
Лагранж исследовал теорию квадратичных форм. При выводе уравнения частот в
случае системы со многими переменными Лагранж допустил ошибку, не исправленную
в течение 70 лет (независимо друг от друга ее заметили К. Вейерштрасс и О. И.
Сомов в 1858 г.); в случае равных корней он считал, что кроме колебательных
движений существуют и так называемые вековые изменения, когда время t встречается не только под знаком
синуса или косинуса.
В 1773 г., всего за два года до
получения Эйлером общих уравнений движения твердого тела с одной неподвижной
точкой, Лагранж получил интегралы движения тяжелого симметричного тела вокруг
оси симметрии, проходящей через неподвижную точку; в этом случае два главных
центральных момента инерции равны» а третий берется относительно оси,
проходящей через центр тяжести и неподвижную точку. Эта задача была уже решена Эйлером в 1764 г. для
случая, когда центр тяжести совпадал с неподвижное
точкой.
Если в начальный момент вращение совершается вокруг
некоторой оси, проходящей через неподвижную точку, то при отсутствии внешних
сил кинетический момент относительно этой оси является постоянным по величине и
по направлению.
То же самое наблюдается и для кинетического момента
относительно оси симметрии, который равен проекции на эту ось начального
кинетического момента. Но если начальный момент и его проекция на ось симметрии
все время являются постоянными, то это показывает, что угол между этими осями
(угол нутации) тоже постоянный, так что угловая скорость нутации окажется равной
нулю.
Таким образом, получающееся движение можно
рассматривать как результат сложения двух вращений: одно совершается с
постоянной угловой скоростью вокруг оси симметрии, а другое заставляет эту ось
описывать конус вокруг неподвижной начальной оси тоже с постоянной угловой
скоростью (прецессия). Получается так называемая регулярная прецессия —
движение, в котором угловая скорость нутации равна нулю, а скорости прецессии и
собственного вращения имеют постоянные величины.
Лагранжу принадлежат также
многочисленные работы по механике сплошной среды. В «Аналитической механике»
немало места уделено гидростатике, гидродинамике, теории упругости. В этих
разделах Лагранж систематизировал все результаты, полученные им и его
предшественниками. В теории упругости Лагранж не располагал общими уравнениями
(они были выведены позже, в 20-е годы XIX в.) и рассматривал равновесие и колебания около положения
равновесия упругих тел одномерных или двумерных – типа нити, струны, мембраны.
В гидродинамике Лагранж оперировал уравнениями для идеальной жидкости (т. е.
совершенно лишенной внутреннего трения), выведенными для него Эйлером.
Математические трудности тут оказались настолько большими, что в общем случае Лагранж мог предложить только приближенный способ решения уравнения движения. Понадобилось немало времени, чтобы с помощью новых математических методов добиться дальнейших результатов там, где вынужден был остановиться такой гениальный ученый, как Лагранж.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
