Главная
Тема 37. Принцип
Гамильтона
Одним из замечательных математиков и
талантливейшим человеком XIX в. был Вильям
Роуэн Гамильтон (1805—1865). Он родился в
Дублине. В четырехлетнем возрасте он неплохо знал географию
и свободно читал литературу на английском языке, а восьми лет овладел
итальянским и французским языками, изучал арабский, санскрит и латынь. К
12 годам он владел уже двенадцатью языками, в том числе персидским и арабским.
Когда ему было 10 лет, он прочитал Евклида в латинском переводе, в 13 лет он
изучил ньютонову «Универсальную арифметику», в 16 лет
познакомился с его «Началами»» а в 17 лет приступил к изучению «Небесной
механики» Лапласа. В 22 года он стал профессором астрономии Дублинского университета,
занялся усовершенствованием астрономических приборов и приступил к оптическим
исследованиям. Особенно большую склонность проявлял
юноша к математике.
В 1824 г. Гамильтон поступил
в Тринити – колледж Дублинского университета, где успешно изучал математические
науки и разрабатывал геометрическую оптику, или теорию лучей. В возрасте 22 лет
молодой ученый был назначен профессором астрономии колледжа св. Андрея
Дублинского университета и королевским астрономом Ирландии. В течение ряда лет
он возглавлял также Дублинскую астрономическую обсерваторию и читал лекции по
астрономии.
В 1837 г. Гамильтон был
избран президентом Ирландской академии наук. Научные заслуги его нашли широкое
признание во всем мире. В частности, в 1838 г. он был избран членом-корреспондентом
Петербургской академии наук.
В 1828 г. в «Известиях»
Ирландской академии наук Гамильтон опубликовал одну из своих самых знаменитых
работ - «Теорию систем лучей». Исследуя системы оптических лучей, он исходил прежде всего из практических запросов их применения
в оптических приборах. В третьем добавлении к этому труду ученый на основании
сложных математических вычислений предсказал существование нового, до тех пор
неизвестного явления – внешней и внутренней конической рефракции в двухосных
кристаллах. Открытие Гамильтона вызвало огромный интерес и впоследствии
сравнивалось с открытием планеты Нептун на основе вычислений Леверье.
В это время в Западной Европе шла борьба между ньютоновской теорией истечения света и теорией
волнообразного распространения света в эфире, которую
разрабатывал Френель. Как аналитик Гамильтон пользовался обеими теориями,
стремясь создать общую теорию.
Основной его идеей был принцип Ферма, гласивший, что
при распространении света в различных средах переход светового луча из начальной
точки в конечную совершается в кратчайшее время.
Покажем, как этот принцип применяется при исследовании преломления света.
Установленные голландцем Снеллием
законы преломления света формулируются так.
1. Направления падающего и преломленного луча находятся
в одной плоскости с нормалью к поверхности раздела обеих сред в точке падения.
2. При переходе света из пустоты в какую-либо среду
отношение синусов углов, образованных падающим и преломленным лучами с
нормалью, есть величина постоянная, называемая коэффициентом преломления в
веществе этой среды.
3. Если свет переходит из среды с коэффициентом
преломления n1 в среду с
коэффициентом преломления n2,
то отношение синусов углов падения и преломления равно обратному отношению
коэффициентов преломления обеих сред.
Пусть SS
(рис. 40) представляет сечение плоскостью чертежа поверхности, разделяющей эти
среды.
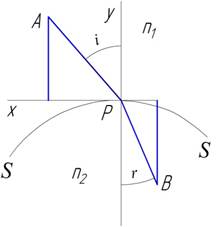
Рис. 40
Уравнение этой кривой в некоторой системе координат
φ(x, у) = 0. Пусть световой луч идет из точки А в среде с коэффициентом
преломления n1 в точку В среды с коэффициентом преломления n2. Если Р — точка пересечения луча и
поверхности раздела, а ось у совпадает с нормалью к этой поверхности в точке Р, то отношение синусов угла падения i и угла преломления r равно
![]()
Заметим, что если скорость распространения света в
пустоте принять за единицу, то скорость света в какой-либо среде равна обратной
величине ее коэффициента преломления п. Тогда время распространения света из А в В определится
суммой
![]()
Покажем, что эта сумма имеет наименьшую величину,
когда справедливо равенство (1).
Пусть точки А,
В, Р имеют координаты A(a1, b1), В (a2, b2) и Р(х,
у). Сумма а выразится равенством
![]()
Будем считать х
независимым переменным. Неизвестные
координаты х и у точки Р должны удовлетворять уравнениям
![]()
![]()
Из этих уравнений определяем координаты х, у
точки Р и переносим в нее начало
координат так, чтобы ось у совпадала
с направлением нормали к S в точке Р, а ось х была направлена по касательной к S в ту сторону, где координаты точки А положительна.
Тогда в точке Р получим
![]()
а
новые координаты точек А и В приобретут вид
![]()
Выражение для ![]() принимает вид
принимает вид
![]()
откуда
![]()
что
получается из выражения закона (1).
Если луч света проходит через несколько сред с
различными коэффициентами преломления, то, разбив его траекторию на бесконечно
малые участки ds
и помножив их на соответствующие коэффициенты преломления n, для суммы σ
получим выражение

Траектория распространения света определится из
условия обращения этого интеграла в минимум.
Но рассматривая принцип наименьшего действия Мопертюи — Эйлера для движения материальной точки с массой т, получаем интеграл
![]()
который обращается в минимум. Так как масса т
есть величина постоянная, то движение материальной точки определяется
интегралом
![]()
который
только значением букв отличается от интеграла, характеризующего распространение
света. Получена оптико-механическая аналогия Гамильтона: движение материальной
точки и распространение света формально определяются одним и тем же законом.
Этот закон справедлив для распространения света в
изотропной среде. В анизотропных средах скорости распространения света (или
частицы) по различным направлениям неодинаковы. Если принять волновую теорию
света, то свет получается в результате колебательных движений упругого
светового эфира. Здесь основную роль должна была сыграть теория упругости, в
частности понятие о главных осях тензора упругости.
Перенесенные в область световых колебаний, эти три оси
получили название оптических осей упругости — направлений, по которым световые
волны распространяются с одинаковой скоростью, не зависящей от направления
колебаний в волновом фронте. Так как анизотропными телами являются
прежде всего кристаллы, то эти три направления получили название оптических
осей кристалла.
Световые колебания, по теории Френеля, совершались
перпендикулярно к направлению луча (поперечные колебания); при вхождении в
кристалл каждое колебание разбивалось на два, совершавшихся в плоскостях,
определяемых направлениями главных осей. Таким образом, получались два пучка так называемого поляризованного света, колебания
которых возникли в двух взаимно перпендикулярных плоскостях. Эти два луча
распространялись с различными скоростями; один из них — так называемый
обыкновенный луч — подчинялся обычным законам преломления, другой луч»
получивший название необыкновенного, им не подчинялся. Явление двойного лучепреломления
было замечено еще Гюйгенсом, который нашел, что оба эти луча имеют различные
волновые поверхности, сечения которых плоскостью, перпендикулярной к
направлению луча, для обыкновенного луча образуют окружность, а для
необыкновенного — эллипс. В развитие идей Гюйгенса Френель построил сложную
волновую поверхность, состоявшую из двух частей — сферы и эллипсоида.
Если направление светового луча совпадало с
напряжением той главной оптической оси, для которой главная оптическая
упругость является наибольшей, то сечение волновой поверхности, производившееся
плоскостью, перпендикулярной к этому направлению, представляло совокупность
круга и эллипса, пересекавшихся в четырех точках. Если вблизи места пересечения
провести общую касательную к кругу и эллипсу, то Гамильтон доказал, что
касательная плоскость к волновой поверхности, проходящая через две полученные
точки касания с кругом и эллипсом, касается волновой поверхности по окружности,
диаметр которой и представляет расстояние между двумя упомянутыми точками.
Каждой точке соприкосновения волновой поверхности с касательной плоскостью
соответствует световой луч; следовательно, должен образоваться полный конус
лучей, расходящихся из центра волновой поверхности и проходящих через
окружность касания. Эти лучи, преломляясь при выходе из кристалла в воздух,
должны быть параллельными и образовать полный цилиндр. Это явление носит
название внутренней конической рефракции; предсказанное Гамильтоном
теоретически, оно было подтверждено опытом, произведенным Ллойдом.
Кроме внутренней конической рефракции существует и внешняя. В каждой из указанных четырех точек пересечения
круга и эллипса в плоскости, проходящей через остальные две главные оси,
волновая поверхность представляет своего рода маленький конус. Поверхность этого
конуса является обертывающей бесконечно большого числа касательных плоскостей,
перпендикулярных к направлениям выходящих лучей; последние по выходе из
кристалла образуют полный конус; это явление и носит название внешней
конической рефракции; оно также было подтверждено на опыте Ллойдом.
Данное исследование было проведено Гамильтоном и
изложено в работе «Теория систем лучей» и в появившихся позднее трех
«Дополнениях».
Оптические работы дали основной толчок к созданию
принципа наименьшего действия в форме Гамильтона; к этому периоду относятся
работы «Об общем методе в динамике» (1834) и «Второй очерк об общем методе в
динамике» (1835).
Руководствуясь идеей
оптико-механической аналогии, усматривая ее прежде
всего в единой математической форме законов движения лучей и материальных
частиц, Гамильтон использует в механике так называемый принцип наименьшего
действия. Применяя этот принцип к определенным явлениям, Гамильтон исходил из
того, что для действительного, осуществляющегося движения тел величина, равная
произведению энергии на время и названная им «действием», должна иметь
некоторое минимальное значение.
Принцип Гамильтона формулируется так. Пусть дана
система материальных точек массами тi и стационарными связями;
пусть на эти точки действуют силы, обладающие силовой функцией U. Известны положения всех точек системы
в начальный момент t1 и в
конечный момент t2. Если Т — кинетическая энергия этой системы, a
L — функция Лагранжа
![]()
то
действием, по Гамильтону, называется интеграл

Все точки системы из начального положения в конечное можно перевести различными путями. Выберем из них
те, для которых переход этот совершается в одно и то же время. Тогда
действительный переход системы из начального положения в конечное совершится,
если действие по Гамильтону будет иметь наименьшую величину.
Принцип Гамильтона можно вывести непосредственно из
принципа Д'Аламбера. Для краткости используем следующие обозначения:
вместо сумм, распространенных на все значения аi от i = 1 до i = n, используем только один член суммы с сохранением индекса i например,

Если ![]() — сила, действующая на точку массой mi, то
уравнение, выражающее принцип Д'Аламбера, примет вид
— сила, действующая на точку массой mi, то
уравнение, выражающее принцип Д'Аламбера, примет вид
![]() (1)
(1)
где
величины Fi
и δri-
соответствуют Хi и δxi основной формулы.
Если имеется силовая функция, U, то сумму элементарных работ действующих сил ![]() можно
представить так:
можно
представить так:
![]()
Далее
![]()
Воспользовавшись формулой
![]()
это
выражение можно представить в виде
![]()
Но сумма ![]() есть не что иное, как вариация δT суммы
есть не что иное, как вариация δT суммы ![]() Таким образом,
исходное уравнение (1) можно выразить так:
Таким образом,
исходное уравнение (1) можно выразить так:
![]()
Помножим обе части этого уравнения на dt и проинтегрируем
в постоянных пределах от t1
до t2:

Но так как в моменты t1 и t2
точки системы имеют вполне определенные положения, то для этих моментов
вариации δri
должны быть равны нулю; таким образом, окончательно получаем

Если вариация переменной величины равна нулю, то это
значит, что соответствующая величина имеет или максимум, или минимум. Максимум
исключается вследствие того, что кинетическая энергия Т может увеличиваться как угодно
далеко; таким образом, остается только одна возможность — минимум, а это и есть
принцип Гамильтона.
Из принципа Гамильтона очень легко получить уравнения
Лагранжа в обобщенных координатах qi
![]()
Эти уравнения можно распространить и на случай, когда
некоторые силы Qi непотенциальны;
в таком случае уравнения Лагранжа принимают вид
![]()
На случай нестационарных связей принцип
Гамильтона был распространен в 1848 г. М. В. Остроградским; поэтому его называют принципом Гамильтона —
Остроградского. Он оказался мощным математическим
оружием физики и был широко использован в работах Максвелла, Гельмгольца, Умова, Эйнштейна, де Бройля, Шредингера и других ученых.
Перейдя к механике, Гамильтон
показал значение в ней своего нового вариационного принципа, а его
характеристическая функция для задач механики (функция Гамильтона Н) оказалась
при довольно широких условиях совпадающей с энергией механической системы.
Зная, как выражается функция Н через координаты и импульсы составляющих
систему материальных точек, можно сразу составить дифференциальные уравнения,
определяющие координаты и импульсы. Получающаяся система дифференциальных
уравнений («канонические уравнения») равносильна системе уравнений движения, в
частности – системе уравнений Лагранжа второго рода, но обладает некоторыми
особыми свойствами, облегчающими ее исследование.
Канонические уравнения были впервые даны Гамильтоном.
Функция Лагранжа L(q, q, t)
выражалась в трех переменных; Гамильтон вместо q ввел новое переменное — обобщенный импульс р, определяемый из уравнения
![]()
Из этого уравнения можно было определить ![]() в функции р, q и t и подставить в функцию Гамильтона:
в функции р, q и t и подставить в функцию Гамильтона:
![]() ,
,
которая
таким образом выражалась в функции переменных р, q, t. Полученные уравнения — теперь уже первого порядка —
представлялись в виде
![]()
![]()
Их было вдвое больше, чем соответствующих уравнений
Лагранжа, но интегрировались они проще: нахождение их интегралов можно было
свести к интегрированию одного уравнения в частных производных первого порядка.
Наконец, Гамильтон связал
свою каноническую систему дифференциальных уравнений первого порядка с
соответствующим дифференциальным уравнением в частных производных, которому,
как выяснилось, удовлетворяет его характеристическая функция Н.
Получилась обширная теория. Она дала новую удобную форму уравнений
движения, новый подход к проблеме их решения (интегрирования). Она вскрывала
более полно и глубоко аналогии между механикой и оптикой, выявила новые
возможности геометрической интерпретации, наконец, она вела к выявлению связи
между волновыми и корпускулярными представлениями, но последнее достаточно
полно раскрылось лишь через столетие.
Необходимо сказать, что
описанная выше теория не была дана Гамильтоном в достаточно общем и законченном
виде: он вел свои исследования, переходя к механике, преимущественно в
предположении, что имеет дело с системой свободных материальных точек,
взаимодействующих с силами, зависящими только от взаимных расстояний.
Дальнейшее развитие следствий из принципа Гамильтона
было сделано Карлом Густавом Якоби
(1804—1851), братом известного Русского физика Б. С. Якоби (1801—1874); его «Лекции по динамике», прочитанные в
1842—1843 гг., были изданы только после его смерти. Основное направление этого
развития заключалось в составлении новых так называемых канонических уравнений
и способов их интегрирования. Поэтому часто можно
встретить в литературе термин «теория Гамильтона – Якоби», но исторически более
справедливо говорить о теории Гамильтона – Якоби – Остроградского.
Эта теория является основным
достижением аналитической механики XIX в. Поначалу казалось, что ее главное значение в развитии
аналитических методов. Но более глубокое выявление связи механики с оптикой и
раскрытие возможности нового геометрического истолкования механических проблем
имели принципиальное значение. Во второй половине XIX в. накопление новых фактов и разработка
новых методов в аналитической механике шло главным образом по линии
геометризации. В начале XX столетия, когда это направление сочеталось с новыми течениями в
физике, именно на созданной им основе были пересмотрены основные понятия
классической механики.
Труды Гамильтона по механике
получили высокую оценку. В 1842 г. на ежегодном собрании Британской ассоциации
в Манчестере К. Якоби сказал: «Гамильтон – это Лагранж вашей страны». В 1866 г.
Тэт охарактеризовал работу Гамильтона по динамике как «крупнейшее дополнение,
полученное теоретической динамикой с тех пор, как были достигнуты великие
успехи Ньютоном и Лагранжем». В 1835 г. Гамильтон был награжден золотой медалью
Английского королевского общества.
Гамильтона всегда привлекала
проблема мнимых величин, значение и геометрическая природа которых не были ясны
математикам того времени. Замечательным вкладом в науку явилось открытие им в
1843 г. исчисления кватернионов – своеобразной системы чисел, представляющей
собой обобщенную комплексную величину, которая состоит из суммы четырех членов.
Первый член был назван ученым скаляром, три остальных - векторами (термин,
введенный Гамильтоном и получивший широкое распространение в физике, механике и
технических науках). В основе арифметики кватернионов лежат не две единицы, как
в арифметике комплексных чисел (т. е. действительная и мнимая единицы), а
четыре, операции над которыми подчинены определенным законам. Особые трудности
представило для Гамильтона установление закона умножения кватернионов, который
он нашел много времени спустя после того, как разработал правила их сложения и
вычитания.
Гамильтон с большой глубиной
и подробностью разработал теорию кватернионов, ее приложения в геометрии и
механике, а также кватернионный и векторный анализы.
Развитию этой теории он посвятил почти целиком последние 22 года своей жизни. В
1853 г. был опубликован капитальный труд Гамильтона по этой теории под
названием «Лекции о кватернионах».
Историческая роль этой работы
велика: во-первых, в ней заложены основы нынешнего векторного исчисления;
во-вторых, теория кватернионов Гамильтона является одним из главных источников
развития такой отрасли математики, как некоммутативная алгебра, т. е. алгебра,
в которой не действует переместительный закон умножения. Такая некоммутативная
алгебра получила широкое применение в современной теоретической физике.
Последний период жизни Гамильтон посвятил разработке
теории кватернионов, которую он не успел довести до конца. Его «Lectures on
Quaternions» были дописаны его учениками. Его теория пользовалась успехом в
некоторых математических кругах; предполагалось даже, подобно теории функций
комплексного переменного, создать аналогичную теорию для кватернионов. Однако
во второй половине XIX в. эти попытки успеха не имели, но так называемый
четырехвектор теории относительности, где имеется три действительных вектора по
трем измерениям пространства и мнимая единица для времени, удобнее было бы
интерпретировать как гамильтоновский кватернион.
Отметим, что в России Гамильтон получил больше признания,
чем в Западной Европе. В 1838 г. по предложению академиков Остроградского,
Буняковского и Фусса он был избран членом-корреспондентом Российской Академии
наук за работу «Об общем методе в динамике, при помощи которого исследование
движения всех свободных систем притягивающихся или отталкивающихся точек
приводится к отысканию и дифференцированию основной зависимости или
характеристической функции».
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов