Главная

Тема 42. А.М.Ляпунов. Устойчивость движения

Основной работой A. М. Ляпунова (1857—1918) была теория устойчивости движения.

Первым этапом в решении задачи на равновесие было определение положения равновесия, или закона движения тела; стали решаться задачи на равновесие тел или механической системы. После определения положения равновесия вставал вопрос: будет ли найденное положение соответствовать устойчивому или неустойчивому равновесий)? Практическое значение могли иметь только устойчивые положения; они характеризовались тем, что находящиеся в таком положении тела при небольшом отклонений автоматически возвращались в положение равновесия. Может быть впервые такая задача была поставлена в приписываемых Аристотелю «Механических проблемах».

Такой же задачей занимался и Архимед, рассматривавший положение равновесия тяжелого параболического сегмента, плававшего в жидкости различной плотности; как истинный практик Архимед рассматривал лишь устойчивые положения равновесия, проверяя, может ли рассматриваемое тело, будучи выведено из положения равновесия, самостоятельно в него вернуться.

После него во избежание затруднительной работы стремились получить критерий, при помощи которого можно было бы без расчетов определить, будет ли данное положение равновесия устойчивым или нет. Первый такой критерий для механической системы тел, находящихся под действием силы тяжести, дал ученик Галилея Торричелли (1608 — 1647); он указал, что устойчивое равновесие соответствует таким положениям системы, в которых высота центра тяжести имеет минимальное значение. Для часто встречающегося случая, когда тяжелое тело имеет только одну точку опоры, принцип Торричелли толковался так, что устойчивое положение равновесия получается, когда центр тяжести находится ниже точки опоры.

Обобщение второго принципа для сил, обладающих силовой функцией, было дано теоремой Дирихле (1805—1859).

Случай устойчивости равновесия системы тел, имеющей несколько степеней свободы, был рассмотрен Лагранжем при помощи обычного в настоящее время приема — «первого приближения, когда дело сводилось к рассмотрению системы линейных дифференциальных уравнений; если для небольших отклонений получались уравнения, соответствующие гармоническим колебаниям, то положение равновесия считалось устойчивым. Для этого требовалось, чтобы корни характеристического уравнения, при помощи которого определяются возможные периоды колебаний, были мнимыми.

Вопрос об устойчивости движения возник в XVIII в. на чисто астрономической почве. После того как было установлено, что движения небесных тел не являются вечными «по своей природе», а совершаются под действием сил всемирного тяготения, необходимо было решить, можно ли считать эти движения устойчивыми. Имелось в виду только периодическое движение планет, совершающееся по эллипсам, близким к окружностям. Если рассматривать движение только под действием силы притяжения Солнца, то возможности падения планеты на Солнце или, наоборот, удаления от него устранялись при помощи законов площадей и сохранения энергии; при наличии трансверсальной скорости планета, приближаясь к Солнцу, увеличивала свою скорость и таким образом ускользала от него; при удалении же от Солнца ее скорость тормозилась работой силы притяжения к Солнцу и планета должна была возвращаться к нему.

Однако на планеты кроме Солнца действуют также силы притяжения и других планет. Если эти возмущения будут все время действовать в одном и том же направлении, то кроме возмущений, носящих характер колебательных движений и со временем не могущих превзойти некоторой предельной величины, могут возникнуть и вековые возмущения, способные произвести с течением времени очень заметное изменение в движении рассматриваемой планеты. Исследованием этих возмущений занялся Лаплас, показавший в своей «Небесной механике», что для Солнечной системы вековые возмущения незначительны и устойчивость движений всех планет можно считать обеспеченной на очень долгое время.

Планеты далеко не всегда можно рассматривать как материальные точки; в действительности они даже являются не сферами, а всего лишь сфероидами. Таким образом, встает вопрос об устойчивости движений тел конечных размеров. Впервые этот вопрос возник при исследовании движения твердого тела в случае Пуансо — Эйлера. Было показано, что без воздействия посторонних сил тела могут вращаться только вокруг осей, совпадающих с главными центральными осями инерции, причем устойчивыми будут вращения только вокруг осей, для которых момент инерции является или наибольшим, или наименьшим.

Развитие машинной техники в XIX в. поставило еще одну задачу — регулирование хода машин, а именно получение равномерной скорости (или близкой к равномерной), когда действующие силы являются переменными. Простейшим таким прибором является обыкновенный маховик, снимающий избыток кинетической энергии при ускоренном движении и вновь отдающий его при замедлении. Затем последовали и другие типы регуляторов, изучение которых стало предметом особой дисциплины — теории регулирования хода машин. В последнее время эти вопросы стали еще более актуальными в связи с проведением автоматизации в различных отраслях промышленности: наряду с обыкновенным возникло еще автоматическое регулирование хода машин, которое развивается особенно быстро в связи с успехами строительства и оборудования скоростных самолетов и спутников.

Вопрос об автоматизации управления ставит новые задачи перед механикой. С одной стороны, заданное движение можно поддерживать путем автоматических силовых воздействий — автоматическое регулирование; с другой стороны, можно сохранить имеющееся движение при помехах и возмущениях со стороны внешних факторов, не зависящих от воли человека. Определением прочности или устойчивости движения против случайных возмущений, имеющих небольшую величину, занимались Раус (Routh), Н. Е. Жуковский, Анри Пуанкаре, но наибольшие успехи сделал А. М. Ляпунов.

А. М. Ляпунов родился 25 мая 1857 г. в Ярославле. Его отец окончивший Казанский университет, работал в нем сначала в качестве астронома-наблюдателя, а потом заведующим обсерваторией. В 1856 г. он переселился в Ярославль, где стал директором Демидовского лицея. Кроме старшего сына Александра он имел еще двоих: Сергея (1859—1924), известного композитора, и Бориса (1864—1942), действительного члена Академии наук по славянской филологии.

Первоначальное образование А. М. Ляпунов получил у отца, а потом у дяди по материнской линии Р. М. Сеченова, брата знаменитого физиолога. По окончании гимназии в Нижнем Новгороде в 1876 г. с золотой медалью он поступил в Петербургский университет на физико-математический факультет, сначала на естественное отделение, но уже через месяц перешел на математическое.

В это время главой Петербургской школы математиков был П. Л. Чебышев, оказавший на А. М. Ляпунова очень большое влияние. После окончания А. М. Ляпуновым университета в 1880 г. П. Л. Чебышев предложил ему заняться исследованиями относительно фигуры небесных тел. Первое решение этой задачи было дано Клеро и затем Лапласом. Рассматривая форму планеты как поверхность уровня в силовом поле под действием сил ньютонова тяготения и центробежной силы во вращении вокруг оси планеты, Клеро и Лаплас пришли к выводу, что поверхность Земли должна иметь форму эллипсоида вращения. Однако при некоторой величине угловой скорости эллипсоидальные формы перестают служить устойчивыми формами равновесия вращающейся жидкости. П. Л. Чебышев поставил задачу так: не переходят ли они при этом в какие-нибудь новые формы равновесия, которые при малом увеличении угловой скорости мало отличались бы от эллипсоидов?

После некоторых попыток A. AL Ляпунов отложил полное решение этой задачи, ограничившись магистерской диссертацией «Об устойчивости эллипсоидальных форм равновесия». Защитив успешно диссертацию, А. М. Ляпунов становится заведующим кафедрой теоретической механики в Харьковском университете. В это время им была подготовлена докторская диссертация «Общая задача об устойчивости равновесия», защищенная им в 1892 г.

Теоретически вычисленные уравнения движения механической системы могут отклоняться от реально получающихся в результате действия внешних факторов — неточности в задании начальных условий, необходимых при получении интегралов для уравнений движения, и от других факторов, действующих во время движения и вызывающих случайные, как правило, весьма незначительные отклонения.

Начнем с простейшего случая. Пусть дана механическая система, положение которой определяется одной обобщенной координатой q. Если известны силы, действующие на систему, а также некоторые начальные условия, а именно значения q_o и q'₀ обобщенных координаты и скорости для некоторого момента t = t₀, то можно определить закон изменения координаты q, проинтегрировав соответствующее дифференциальное уравнение

(1)

Пусть полученный интеграл имеет вид

(2)

Назовем определенное этим уравнением движение невозмущенным.

Предположим теперь, что начальные значения q_o и определены неточно или изменились вследствие неуточненных случайных и временных воздействий; действительные их значения q_о + ε и , где ε и — так называемые начальные возмущения, величина которых неизвестна. Если знать эту величину, подставив соответствующие значения в уравнение (1) и проинтегрировав, получим другой закон изменения q, отличный от определенного равенства (2). Получающуюся разность назовем возмущением. Эта разность не должна быть большой, и не только в начальный момент, но и во все время движения при t > t_o. Пусть наибольший допустимый предел ее L:

(3)

Тогда, если можно определить такие достаточно малые положительные числа Е и , чтобы при

и любом имелось неравенство (3), то невозмущенное движение, определяемое (1), будет устойчивым по отношению к координате q. Однако можно потребовать и большего, а именно чтобы и обобщенная скорость тоже не превышала бы некоторого допустимого предела ; если это имеет место при тех же предельных значениях Е и , то движение будет устойчиво по отношению к координатам q и .

Пусть теперь положение системы определяется п обобщенными координатами q_i. Тогда движение системы определится п уравнениями вида (1), и при некоторых начальных условиях и получим всего п решений:

Соответствующие уравнения определят невозмущенные движения. Если п пар начальных значений координат и скоростей q_i, _i. получат п пар начальных возмущений и предельные значения которых не должны превышать соответственно п пар значений Е_i и то невозмущенное движение будет устойчивым для n координат q_i если за все время движения существуют неравенства

соответствующие возмущения можно обозначить

Кроме того, можно потребовать устойчивости и по отношение к обобщенным скоростям.

Пусть имеются s соотношений вида , которые при начальных значениях координат и скоростей имеют вид Если начальные возмущения и - для всех удовлетворяют п парам неравенств

и s разностям

и не превышают соответственно заданных пределов L₁, ..., L_s, то невозмущенное движение называется устойчивым по отношению к системе Ф₁, ..., Ф_s.

Обыкновенно полагают так что s = 2nя; в таком случае невозмущенное движение будет устойчиво по отношению к обобщенным координатам и скоростям.

Пусть уравнения движения механической системы даны в виде

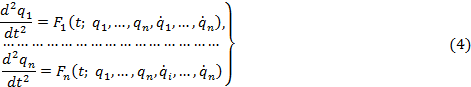
и соответствующие решения для невозмущенного движения имеют вид

В возмущенном движении величины имеют другие значения; обозначим разности между соответствующими координатами в возмущенном и невозмущенном движениях x_i:

(5)

Эти разности представят вЬзмущения обобщенных координат. Продифференцировав эти равенства один раз, получим возмущения обобщенных скоростей. Продифференцировав их еще один раз, получим дифференциальные уравнения возмущенного движения вида

(6)

которые можно представить так:

Выражение Q_i(t) представляет не что иное, как правую часть соответствующего уравнения из системы (4), где все q_i, и заменены выражениями f_i(t) и .

Возмущенные значения координат и скоростей

и

Таким образом, правую часть равенства (6) можно представить как функцию от времени t, возмущений х_i и их производных .Обозначив ее Х_i получим систему п уравнений:

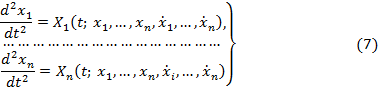
Из системы (7) получаем дифференциальные уравнения возмущенного движения. Так как правые части этих уравнений получились из разностей q_i — f_i(t) соответствующих координат в возмущенном и невозмущенном движениях, а также из производных этих разностей, то при всех x_i = 0, т. е. когда возмущенное движение переходит в невозмущенное, уравнения (7) удовлетворяются.

Если введем обозначения

то систему п уравнений второго порядка (7) можно заменить системой 2n уравнений первого порядка:

(7^/)

Так как совокупность равенств x₁ = x₂ = ... = 0 представляет решение системы (7'), то невозмущенное движение определяется нулевыми решениями системы дифференциальных уравнений возмущенного движения. Таким образом, любая задача на определение устойчивости рассматриваемого движения, или в частном случае равновесия, сводится к единообразной математической, задаче об устойчивости нулевых решений некоторой системы дифференциальных уравнений.

Приведем теперь некоторые примеры. Будет ли устойчивым движение материальной точки, масса которой равна единице; движение определяется уравнением

Полагая , получаем уравнения

Так как оба они имеют решение х = у = 0, то придется исследовать устойчивость нулевого решения. Но если невозмущенное решение соответствует равновесию точки в начале координат, то x и у представляют эти возмущения. В качестве начальных условий берем произвольные числа x₀ и у₀ и интегрируем дифференциальные уравнения возмущений:

Если умножить обе части первого уравнения на k, а затем возвести оба полученных уравнения в квадрат и сложить, то будем иметь

Это показывает, что , . Так как х₀ и у₀ можно выбрать сколь угодно малыми, то это значит, что определяемое полученным уравнением невозмущенное движение является устойчивым.

Возьмем теперь дифференциальные уравнения возмущенного движения в таком виде:

где α > 0. При начальных условиях t = 0, х = x₀, у = y₀ интеграция уравнений дает решения

Так как при α > 0 первые два члена с увеличением t беспредельно возрастают, то убеждаемся, что решение х = у = 0 неустойчиво.

Однако если ввести дополнительное условие

то сумма

окажется при некотором значении t меньшей какого-то заданного числа и останется в дальйейшем такой же; тогда получится так называемая условная устойчивость.

Нетрудно видеть, что при t → ∞ величина х² + у² имеет в пределе нуль; это так называемая асимптотическая устойчивость.

Употребленные в рассмотренных примерах выражения представляют так называемые квадратичные формы; под этим термином подразумевается однородный многочлен второй степени относительно переменных представим его в общем виде:

Здесь коэффициенты а_ij не зависят от x_i но могут зависеть от времени t. Исследования знакопостоянства или знакопеременности таких выражений имеют большое значение в исследованиях по теории устойчивости движений. Как видно из предыдущих примеров, имеют значение не только абсолютные величины возмущений, но в основном их пределы.

При помощи рассмотрения указанных квадратичных форм можно определить условия устойчивости или неустойчивости движения даже и в том случае, когда нельзя будет в полной мере найти выражение интеграла основных дифференциальных уравнений рассматриваемого движения.

В 1902 г. А. М. Ляпунов переезжает в Петербург, где он посвящает себя исключительно научным исследованиям.

Основные работы петербургского периода деятельности А. М. Ляпунова относятся к теории фигур небесных тел и форм равновесия равномерно вращающейся жидкости, частицы которой взаимно притягиваются по закону Ньютона. В это время он получил сочинение Анри Пуанкаре о фигурах равновесия жидких масс. Прочтя работу, он убедился, что Пуанкаре остался на тех же самых позициях, которые он занимал 17 лет тому назад. Поэтому А. М. Ляпунов продолжал свои исследования, которые получили особый интерес вследствие того, что они переплелись с новой космогонической теорией, выдвинутой Джорджем Дарвином — сыном знаменитого естествоиспытателя Чарльза Дарвина, — касавшейся происхождения Луны.

Выдвинутая Дж. Дарвином теория приливной эволюции и происхождения Луны заключалась в следующем. Среди всех планетных спутников Луна выделяется своими размерами и массой; это обстоятельство делает трудно приложимой к ней теорию захвата, которой можно объяснить происхождение большого числа планетных спутников.

Рассмотрим механическую систему Земля — Луна. На эти планеты действуют силы притяжения Солнца. Если пренебречь разницей в расстоянии до Солнца от центра Земли и Луны, то можно считать обе эти планеты имеющими по направлению к Солнцу одинаковые нормальные ускорения; в таком случае относительные движения обеих планет не изменятся и можно считать центр Земли неподвижным; при этом, конечно, сохраняются как вращения обеих планет вокруг собственной оси, так и движение Луны вокруг Земли. В таком случае можно считать постоянным кинетический момент системы, складывающийся из кинетических моментов собственных вращений Земли и Луны вокруг своих осей и кинетического момента движения Луны вокруг Земли.

Так как ближайшие к Луне частицы воды на земной поверхности притягиваются сильнее, чем частицы в центре Земли, а частицы, находящиеся на противоположной стороне Земли, наоборот» слабее, то разность этих сил притяжения обусловливает две приливообразующие силы, которые на ближайшей к Луне части земной поверхности направлены к Луне, а на более отдаленной — наоборот, от Луны. Если считать диаметр Земли весьма малым по сравнению с расстоянием между Землей и Луной, то, дифференцируя формулу, выражающую закон всемирного притяжения, обратно пропорционального квадрату расстояния, нетрудно показать, что приливообразующая сила изменяется обратно пропорционально кубу расстояния. Этим объясняется то обстоятельство, что хотя силы притяжения Земли Солнцем больше, чем Луной, но приливообразующая сила Луны гораздо больше приливообразующей силы Солнца.

Эти две силы оттягивают воды океана в обе стороны от поверхности Земли, образуя приливную волну, которая при вращении Земли вокруг своей оси два раза в сутки обходит вокруг Земли. Действие этой приливной волны, идущей против направления вращения Земли, несколько тормозит вращение Земли (длительность суток незначительно возрастает). То же самое происходило и на Луне. Обе силы, действующие на Землю и на Луну, согласно третьему закону Ньютона, равны, но, поскольку масса и момент инерции Луны гораздо меньше, чем у Земли, действие ч приливов на Луну гораздо больше, чем на Землю. Но если кинетические моменты собственного вращения Земли и Луны уменьшаются, а общий кинетический момент системы сохраняет постоянную величину, то расстояние между Землей и Луной должно со временем увеличиваться, ибо нет причин, которые могли бы увеличить скорость Луны в ее движении вокруг Земли.

Теперь, если рассматривать движение в направлении, обратном течению времени, то можно сделать вывод, что ранее Луна была ближе к Земле и угловые скорости Земли и Луны вокруг своих осей были больше. Вычисления Дж. Дарвина показали, что когда Луна находилась в непосредственной близости к Земле, то продолжительность суток в системе Земля — Луна составляла всего пять часов. Так как исследования Пуанкаре показали, что одной из форм равновесия вращающейся.жидкой массы является грушевидная, а Дарвин определил, что при скорости вращения, соответствующей продолжительности суток около пяти часов, устойчивость грушевидной формы жидкой массы нарушится, то Луна — меньшая часть груши — должна оторваться от остальной части, которая и составит Землю.

Теория приливной эволюции в настоящее время является общепризнанной; она объясняет, почему Луна обращена к Земле всегда одной стороной (угловая скорость собственного вращения Луны одинакова со скоростью ее обращения вокруг Земли).

Однако теория Дж. Дарвина о происхождении Луны не оказалась справедливой. А. М. Ляпунов показал, что Пуанкаре и Дарвин в своих исследованиях применяли только первые приближения, и отброшенные ими члены в действительности могли иметь такую величину, что делают результаты, полученные Дарвином, невозможными, а именно грушевидная форма равновесия была неустойчивой с самого начала и, следовательно, не могла образоваться.

В дальнейшем английский астроном Джине произвел пересмотр вычислений Дарвина по приближенным формулам. Ему удалось обнаружить в вычислениях Дарвина пренебрежение членами, которые сам Дарвин считал ничтожными, но которые в действительности оказались достаточно большими. Когда было произведено вторичное вычисление уже по формулам второго приближения, то полученные результаты оказались в полном согласии с теорией Ляпунова.

Материал, касающийся фигур равновесия жидкой массы, опубликованный за период 1905—1918 г. и только в «Записках Русской Академии наук», составляет около 750 страниц текста. Разработка оставленного Ляпуновым материала представляет громадную задачу, которая выполняется его последователями как в нашей стране, так и за рубежом.

В настоящее время теория устойчивости Ляпунова является одним из сильнейших математических средств в исследованиях, касающихся космических полетов.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00