Главная
Тема 43. Н.Е.Жуковский. Возникновение экспериментальной
аэродинамики
Отец русской авиации Н. Е. Жуковский родился 17 января 1847 г. в деревне Орехово
Владимирской губернии. Он был сыном инженера по дорожному строительству.
Первоначальное образование он со своим старшим братом получил в семье; их
учителем был замечательный педагог А. X. Репман,
естествоиспытатель по специальности, который научил Николая Егоровича понимать
и любить природу. Живое чувство природы не оставляло ученого в течение всей
жизни и оно ясно обозначается в его научно-исследовательской деятельности: он
умел наблюдать и выделять наиболее важные черты, определяющие изучаемое
явление. В 1857 г. он вместе со старшим братом поступил в Московскую гимназию.
Первые два года будущий ученый не выказывал больших успехов. Но в третьем
классе, где математику стал преподавать известный автор учебников А. Ф. Малинин и началось изложение геометрии, Николай Егорович
показал недюжинные геометрические способности и окончил гимназию в 1864 г. с
серебряной медалью.
После окончания гимназии ему пришлось поступить на
физико-математический факультет Московского университета, что он сделал с очень
большой неохотой, так как не чувствовал в себе никакого призвания к
преподавательской деятельности.
В середине XIX в. в Московском университете, как и
вообще в России, основное направление в преподавании механики было главным
образом аналитическое — по Лагранжу. Определяющим было влияние М. В.
Остроградского, идеи которого развивал Н. Д. Брашман
— основатель Московского математического общества. Нельзя сказать, чтобы
геометрические идеи Пуансо были совершенно неизвестны
в Московском университете, но все-таки они стояли на втором плане.
В Московском университете Н. Е. Жуковскому пришлось
столкнуться с представителями обоих направлений. Теоретическую механику он
слушал у Ф. А. Слудского — последователя
«Аналитической механики» Лагранжа, а также у В. Я. Цингера,
преподававшего на младших курсах математику. В этой борьбе двух направлений Н.
Е. Жуковский определенно стал на сторону геометрического метода, не
пренебрегая, однако, и аналитическим. Его идеи ясно выражены в речи,
произнесенной на 25-летнем юбилее Московского математического общества.
«Отстаивая достоинства геометрического метода
исследования, я далек от мысли об его исключительности. Механика должна
равноправно опираться на анализ и геометрию, заимствуя от них то, что наиболее
подходит к существу задачи... Анализ дает нам могущественное оружие для
разрешения задач динамики. Но последняя обработка решений задачи всегда будет
принадлежать геометрии»
В 1870 г. Н. Е. Жуковский становится преподавателем
физики в Московской второй женской гимназии и увлекается лабораторными работами.
Одновременно он готовится к магистерским экзаменам. После их окончания он
становится доцентом Московского высшего технического училища по кафедре
аналитической механики. В 1876 г. он защищает магистерскую диссертацию на тему
«Кинематика жидкого тела». Таким образом, определилось его основное направление
научной деятельности.
Механика жидкого тела разделялась на две части:
гидростатику и гидродинамику. Как уже известно, гидростатика — учение о
равновесии жидкостей и плавающих в ней тел; ее основы были заложены еще
Архимедом. Дальнейшее ее развитие относится к XVII в., когда основные законы
гидростатики были установлены Стевином и Паскалем. В
XVIII в. законы плавания судов были почти одновременно установлены Эйлером в
его «Морской науке» и Буге, который занялся исследованием условий равновесия
плавающего судна. Общее решение задачи об устойчивости равновесия плавающих тел
было дано Дюпеном и А. Ю. Давидовым.
Что касается теории движения жидкостей —
гидродинамики, то ее положение было значительно менее удовлетворительным.
Первое сочинение по гидродинамике принадлежит Даниилу Бернулли (1700—1782), начало деятельности
которого протекало в Петербургской Академии наук: его основное произведение
«Гидродинамика» вышло в 1738 г. Ему принадлежит уравнение, устанавливающее
связь между скоростью жидкости, движущейся в трубе, и соответствующим
давлением; эта теорема вместе с поправочными коэффициентами является основным
содержанием прикладной гидродинамики — так называемой гидравлики.
Несколько позднее Эйлер и Лагранж дали
дифференциальные уравнения в частных производных, определяющие движение жидкости. Но их интеграция представляла
довольно трудный процесс. Кроме математических,
имелись еще и принципиальные трудности. Подобно тому
как в геометрической статике рассматривается идеальное, так называемое
абсолютно твердое тело, в гидродинамике тоже пришлось установить понятие об
идеальной жидкости. Под этим понятием подразумевалась непрерывная, несжимаемая
жидкость, все части которой могли свободно перемещаться, касаясь друг друга;
последнее требование равнозначно существованию лишь нормальных сил
взаимодействия между частицами; таким образом, силы трения и вязкость жидкости
устранялись. Но в этом случае при обтекании жидкости вокруг заключенного в ней
твердого тела полная сила давления на тело оказывалась равной нулю, что,
конечно, не соответствовало действительности.
Разработкой гидродинамики в течение XIX в. в Западной
Европе занимались три ученых — Августин
Коши (1789—1857), Герман Гельмгольц
(1821—1894) и Густав Кирхгофф
(1824—1887).
Для Коши гидродинамика представляла лишь частный
случай его механики непрерывной среды. Он первый начал разрабатывать механику
непрерывной среды, т. е. механику упругого твердого тела и жидкости. Он первый
стал рассматривать условия равновесия и движения выделенного объема этой среды,
на который действуют объемные и поверхностные силы (силы, действующие на
«единицу объема — массы — тела и на единицу поверхности выделенного объема); в
случае упругого тела ему принадлежит установление шести составляющих напряжения
— трех нормальных и трех тангенциальных, — откуда развивалась теория тензоров.
В случае жидкой частицы он рассматривал не только ее поступательное и
вращательное перемещение, но также и деформации — изменения объема (коэффициент
кубического расширения) и формы, когда сфера переходит в эллипсоид. Он также
выразил в математической форме условие непрерывности среды. Если u, v
и w представляют проекции скорости
частицы на координатные оси, то в случае несжимаемой жидкости условие непрерывности
выражается в форме
или
в современной форме, если ввести символ Гамильтона
как
скалярное произведение символа Гамильтона на вектор скорости 
; это так называемая дивергенция скорости, которая
должна быть равна нулю.
Герман Гельмгольц родился в Потсдаме 12 августа 1821
г. После окончания военно-медицинской академии он посвятил себя изучению
физиологии, не оставляя, однако, механики и физики, которыми он живо
интересовался с самого детства.
В 1847 г. Г. Гельмгольц выпустил работу «О сохранении
силы» (в то время термина «энергия» еще не существовало), которая наряду с
исследованиями Роберта Майера и Джоуля является основополагающей в установлении
закона сохранения энергии. В 1858 г. выходит его работа «Об интегралах
гидродинамических уравнений, соответствующих вихревому движению», которая дает
физическое истолкование элементарных вращений, лишь слегка и притом чисто
аналитически намеченных в работах Коши.
Работы Коши и Гельмгольца предшествовали магистерской
диссертации Н. Е. Жуковского, а научная деятельность Густава Кирхгоффа
развертывалась одновременно с деятельностью Н. Е. Жуковского.
В 1842 г. Г. Кирхгофф поступил на
физико-математический факультет Кенигсбергского университета, в котором
процветала кенигсбергская физико-математическая школа, основанная Францем Нейманом (1798—1895) и
математиком Карлом-Густавом Якоби
(1804—1851), продолжателем динамики Гамильтона. Первые работы Кирхгоффа (1845-г1847) касались
распространения электричества по пластинкам.
В 1876 г. вышли «Лекции по математической физике»
Кирхгоффа, в первом томе которых он изложил математический метод исследования
плоскопараллельных движений жидкостей; видоизменение этого метода было плодом
одной из блестящих гидродинамических работ Н. Е. Жуковского.
Рассмотрим его первую работу по гидродинамике —
магистерскую диссертацию «Кинематику жидкого тела». Во введении к этой работе
Н. Е. Жуковский писал, что в ней дан краткий, но по возможности наглядный очерк
теории скоростей и ускорений непрерывно изменяемого тела. Это можно
рассматривать как вступление в гидродинамику; здесь поставлены общие теоремы о
движении жидкости на уровне развития, которое получили исследования изменяемых
систем частного вида.
В первой главе Н. Е. Жуковский передает результаты,
полученные Коши в его двух основных работах: «О движении или напряжении
твердого тела» и «О распространении волн на поверхности тяжелой жидкости
бесконечной глубины». Он рассматривает все три изменений, указанных Коши: деформацию,
вращение и поступательное перемещение. Всё бесконечно малое движение частицы
слагается из поступательного движения ее центра, из движения, обращающего
бесконечно малый шарик в эллипсоид деформации, бесконечно мало отличающийся от
шара, и из вращения осей деформации.
Составляющие угловых скоростей мгновенного вращения
частицы он получает в виде
В настоящее время вектор угловой скорости 
этого вращения
при помощи символа Гамильтона имеет вид
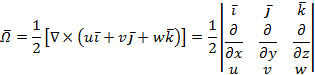
и
называется ротацией скоростей (u, v, w).
Если приравнять это выражение к нулю, то получим
условие, при котором выражение udx + vdy +wdz представляет полный дифференциал.
Это условие вполне аналогично условию о том, что данная система сил X, У, Z допускает силовую функцию U или
потенциальную П
= —U. Полученное выражение для Гельмгольц
назвал вихрем.
Если исключить составляющие скорости, обусловленные
вихрем Ω, то для остающихся скоростей u/, v/ ,w /будем иметь Ω =
О, а это показывает, что скорости u/, v/ ,w/ можно получить как частные
производные от некоторой функции F —
потенциала скоростей — по соответствующим ординатам
Таким образом, остающееся движение получает название
движения с потенциалом скоростей.
После исключения поступательного перемещения,
определяемого движением центра частицы, получаем то, что Н. Е. Жуковский
называет внутренним движением, т. е. чистую деформацию, которую он подробно
рассматривает в остальной части первой главы.
Во второй главе исследуется течение жидкости, а именно
рассматриваются линии и поверхности токов.
Линией тока называем кривую, касательная к которой в
какой-либо точке совпадает со скоростью жидкости в этой точке в рассматриваемый
момент времени t (с изменением t изменяются и линии тока). Поэтому
дифференциальное уравнение линии тока получаются в таком виде:
где
u, v, w — проекции скорости в данной точке
на координатные оси — являются функциями х,
у, z и времени t, которое мы считаем постоянным. Линии тока не следует смешивать с
траекториями движения частиц жидкости. Дифференциальные уравнения траекторий
можно получить, если проинтегрировать уравнения
и
исключить затем время t из полученных
интегралов. В одном лишь важном частном случае линии тока совпадают с
действительными траекториями — при так называемом установившемся движении,
когда линии тока одинаковы для всех значений t. Если u,v
и w независимы от времени t, то обе
приведенные выше системы дифференциальных уравнений совпадают.
Аналогично для составляющих р, q, r вихря можно получить кривую, которую Гельмгольц назвал
вихревой линией. Совокупность прилегающих вихревых линий образует вихревую
струйку, а количество жидкости, протекающей в единицу времени через сечение
такой струйки, называется напряжением вихревой струйки. Это напряжение остается
постоянным по всей длине струйки, и все вихревые струйки или замкнуты, или
имеют концы на поверхности жидкости.
Если окружить струйку замкнутой линией и составить
сумму произведений скорости 
на
соответствующий элемент длины 
линии и на
косинус угла между и , то полученную сумму по всей
замкнутой линии Н. Е. Жуковский называл «обтечением». В настоящее время эта
величина называется циркуляцией; если рассматривать скорость как некоторую
силу, то циркуляцию можно определить как полную работу этой силы при перемещении
по замкнутой линии, окружающей вихревую струйку. Величина циркуляции для всякой
замкнутой линии равна удвоенной сумме напряжений вихревых струек, обхватываемых
этой линией.
Последние две главы посвящены сложению и разложению
течений жидкости, а также ускорениям точек движущейся жидкости.
После защиты магистерской, диссертации Н. Е. Жуковский
получает заграничную командировку (1877), а в 1879 г. он назначается
сверхштатным профессором теоретической механики в МВТУ. В это время Н. Е.
Жуковский сближается с Ф. Е. Орловым, профессором прикладной механики
Московского университета и основателем механического кабинета. Одновременно
расширяются его знакомства с инженерными кругами, и он становится активным
членом Политехнического общества. В это время Н. Е. Жуковский готовится к
докторской диссертации «О прочности движения», которую он с успехом защищает в
1882 г.
После защиты докторской диссертации Н. Е. Жуковский
получает степень доктора и становится приват-доцентом Московского университета,
а затем он выбирается экстраординарным профессором теоретической механики
Московского университета. Пребывание в университете и знакомство с рядом
выдающихся профессоров — физиком А. Г. Столетовым, астрономами Ф. А. Бредихиным
и В. К. Церасским, а также с математиками Б. К. Млодзеевским, В. Я. Цингером и Н.
В. Вугаевым — очень расширили круг интересов Н. Е.
Жуковского.
Он выпускает ряд работ астрономического характера, из
которых особенно интересна большая работа «О движении твердого тела, имеющего
полости, наполненные однородной капельной жидкостью»; в то время эта работа
была удостоена премии Брашмана. В
конце сочинения ставится вопрос: если трение жидкости в полости тела влияет на
его вращение так, что по начальному состоянию можно указать положение оси
вращения, которое она примет по истечении очень продолжительного времени, то не
этой ли теоремой следует объяснить то обстоятельство, что, несмотря на всякие
случайные начальные скорости, планеты вращаются около своих осей инерции?
Основным сочинением по гидродинамике наряду с
«Кинематикой жидкого тела» и «Движением твердого тела с полостями, наполненными
капельной жидкостью» было сочинение, вышедшее в 1890 г., «Видоизменение метода
Кирхгоффа для определения движения жидкости в двух измерениях при постоянной
скорости, данной на неизвестной линии тока».
Рассмотрим плоскопараллельное движение несжимаемой
жидкости, для которого условие непрерывности выражается в виде
где u и v — некоторые функции х и у
представляющие в установившемся движении проекции скорости точки жидкости на
координатные оси.
Если это уравнение представить в виде
то
оно приобретет вид условия, при соблюдении которого выражение —vdx + udy является
полным дифференциалом некоторой функции ψ.
Действительно, положив
получаем,
что производные накрест — от (—v) по у и от u по x
- неравны. Таким образом, после интегрирования уравнения
получаем
интеграл
определяющий
линию тока. Если, кроме того, имеется потенциал скоростей φ, так что
то
нетрудно видеть, что эквипотенциальные поверхности φ = const
и линии тока ψ = const
пересекаются под прямым углом.
Можно показать, что обе функции φ и ψ
удовлетворяют уравнению Лапласа:
Поставленная задача имеет тесную связь с теорией
функций комплексного переменного.
Возьмем выражение Р(х, у)+iQ(x, у). Если надо, чтобы это
выражение представляло функцию от комплексной переменной z = х + yi, то необходимо соблюдение
условий
Обе функции Р и Q, как
нетрудно убедиться, тоже удовлетворяют
уравнению Лапласа.
Выше приведено
Это показывает, что выражение
можно рассматривать как некоторую функцию от
комплексной переменной z = х + уi:
или
Теперь на координатной плоскости z = x + iy дадим х и у — ряд
последовательных значений; тогда определяемая этими координатами точка z опишет на плоскости некоторую кривую
Если возьмем другую плоскость 
, координатные оси которой можно считать параллельными
осям х, у первой плоскости, то,
подставляя в φ и ψ значения х
и у, определявшие на плоскости (x, у) кривую z = F(x, у), получим на плоскости (φ,
ψ) другую кривую, точки которой определятся выражением ω = f (z). Эту кривую можно
рассматривать как получившуюся из первой кривой при помощи преобразования
ω = f(z).
Можно показать, что в этом
преобразовании углы между пересекающимися в одной точке прямыми или кривыми
остаются такими же, как и у первоначальных, т. е. сеть кривых, пересекающихся
под прямыми углами, преобразуется в сеть, соответствующие кривые которой тоже
пересекаются под прямыми углами; преобразованная сеть только расширяется или
сжимается и поворачивается на некоторый угол по сравнению с первоначальной. Такие преобразования, обладающие свойством сохранения
углов, называются конформными.
Таким образом, каждому движению жидкости с потенциалам скоростей при
установившемся движении соответствует некоторая функция комплексной переменной.
Обратно, если имеется некоторая функция комплексной переменной, то, разбив ее
на действительную и мнимую части, при соответствующем выборе условий на
границах, можно получить выражения для потенциала скоростей φ и функции
тока ψ. Все решение задачи зависит от удачного выбора функции f.
Предположим, что на цилиндр радиусом 
набегает
параллельно оси Ох из бесконечности в направлении
отрицательной оси Ох плоскопараллельный
поток со скоростью vo
при х = ∞. В таком случае
решение задачи определится, если возьмем функцию f в таком виде:
где
В таком случае
Семейство линий тока получится, если положим ψ = С. Давая постоянной С различные значения, получим уравнения различных линий тока.
Положив С =
0, получаем
Соответствующая линия тока состоит из двух частей: у = 0 — прямая, совпадающая с осью х, и 
- окружность с
центром в начале координат, лежащем на оси цилиндра. Эта линия тока идет из
бесконечности по направлению отрицательной оси Ох; подходя к цилиндру, она раздваивается, огибает цилиндр, а затем
смыкается и уходит в бесконечность при х = —∞. Эта линия тока определяет
границы потока. Так как функция ψ
удовлетворяет уравнению Лапласа, то по теореме Дирихле, зная значения ψ на границах пространства, можно
определить ее значение во всех точках этого пространства.
В качестве другого примера рассмотрим функцию
где
Тогда
Как видно, линии тока представляют окружности с центром
в начале координат, а эквипотенциальные линии — радиусы, исходящие из начала
координат и перпендикулярные к направлениям скоростей. Получились линии тока
вихря, вращающегося вокруг начала координат в отрицательном направлении, т. е.
по движению часовой стрелки.
Комбинируя функции f соответствующим образом и выбирая
так, чтобы какая-либо линия тока совпадала с контуром пространства,
заполненного жидкостью, можно найти функции φ и ψ, определяющие
течение жидкости в рассматриваемом пространстве.
Знакомство с университетскими астрономами оставило
след в астрономических работах Н. Е. Жуковского, в частности в уже упомянутой
работе «О движении твердых тел с полостями, заполненными жидкостью». Когда Комиссия по увеличению московского водопровода обратилась к
нему с просьбой помочь в ее работе, то Н. Е. Жуковский дал несколько работ,
касающихся исследования движения почвенных вод, в частности классическую работу
«О гидравлическом ударе в водопроводных трубах», позволившую устанавливать
место разрыва водопроводных труб, не дожидаясь, когда вода в месте разрыва
выйдет наружу; эта работа была переведена на английский язык.
После того как математики Московского университета
заинтересовались нахождением частных решений уравнений Эйлера для движения
твердого тела, Н. Е. Жуковский создал ряд работ по гироскопии,
в частности дал геометрическую интерпретацию случая Ковалевской.
Непрерывный ряд исследований Н. Е. Жуковского по
аэродинамике и воздухоплаванию выдвинул его в число передовых ученых как в России, так и за рубежом.
Серьезно заниматься вопросами воздухоплавания Н. Е.
Жуковский начал с 1890 г., когда появилась его первая статья по теории летания.
В этой статье он показывает, что сила тяги самолета может получиться или в
результате трения, или же вследствие срыва струй с движущегося тела,
нарушающего плавное обтекание, которое требуется теорией идеальной жидкости. В
этой статье он склонился в пользу силы трения, но в дальнейшем вопрос был решен
в пользу теории идеальной жидкости с добавлением срыва струй и соответствующего
образования вихрей.
Одна за другой следуют его работы «О парении птиц», «О
наивыгоднейшем наклоне аэропланов» и «О
присоединенных вихрях». В это время уже с изобретением легкого двигателя
внутреннего сгорания экспериментальные и теоретические работы по
воздухоплаванию начинают появляться и в России, и за границей. В 1904 г. один
из учеников Н. Е. Жуковского Д. П. Рябушинский
построил в Кучине Аэродинамический институт, затем строится аэродинамическая
труба в Техническом училище и в Московском университете. В Техническом училище
создается воздухоплавательный кружок, а в 1909—1910 гг. Н. Е. Жуковский читает
там впервые созданный курс «Теоретические основы воздухоплавания».
Ставится серьезно вопрос о причине возникновения
подъемной силы у крыльев, имеющих изгиб кверху. Качественное объяснение причины
этого возникновения было дано еще в 1894 г. английским профессором Ланчестером при помощи толкования известной теоремы
Бернулли, устанавливающей связь между скоростью течения жидкой струи и
возникающим в ней давлением. Он указывал, что на верхней
выпуклой стороне крыла увеличивается скорость протекающей жидкости и
соответственно уменьшается давление; разность давлений на нижней и верхней
поверхностях крыла и является причиной направленной вверх подъемной силы.
Это в основе своей правильное объяснение не позволяло, однако, получить
количественного определения величины подъемной силы для заданного профиля
крыла.
Способ для этого определения был открыт Н. Е.
Жуковским в сентябре 1904 г. в Кучине, когда он наблюдал движение в воздухе
воздушных змеев; у него появилась первая догадка, которая через два года
привела к теореме Жуковского, изложенной в статье «О присоединенных вихрях».
Если на профиле поперечного сечения крыла построить цилиндр с высотой, равной единице,
то в потоке воздуха, набегающего со скоростью v (скорость полета самолета), действующая на этот цилиндр подъемная
сила
где ρ —
плотность воздуха, а Г — циркуляция
по контуру, окружающему профиль.
В дальнейшей работе, произведенной Н. Е. Жуковским и
С. А. Чаплыгиным, установлено, что для образования циркуляции необходимо, чтобы
профиль имел одно острие, а все крыло длиной l — заостренную кромку. В таком случае подъемная сила крыла
выражается формулой
Эта формула не учитывает явлений, происходящих по
обоим концам крыла, при обтекании которых поток изменяет свою форму. Что
касается формул для расчета циркуляции, то соответствующие методы были
разработаны позже С. А. Чаплыгиным.
Так как эти формулы предполагали существование
плоскопараллельного движения, простирающегося в, бесконечность, то следующей
задачей было получить формулы для расчета подъемной силы крыла конечной длины.
Некоторые результаты в этой области были известны С. А. Чаплыгину в 1911 г., но
полное развитие идей Жуковского и Чаплыгина в применении к крылу конечной Длины
было сделано немецким ученым Людвигом Прандтлем.
В это время Н. Е. Жуковский занимался другой, более
сложной теорией, а именно определением силы тяги винта. Кроме избегающего
потока со скоростью v самолета на лопасть винта действовал еще круговой поток,
происходящий от его вращения. Рассматривая фотографии струй, образуемых
вращающимся корабельным винтом в бассейне, Н. Е. Жуковский обратил внимание на
пузырьки воздуха, образовавшие винтовые линии, которые являлись следами
вихревых нитей, сбегавших с лопастей винта. Это послужило основой для создания
им вихревой теории воздушных винтов, которой были посвящены четыре больших мемуара, написанных в 1912—1918 гг.
В 1916 г. при аэродинамической лаборатории Московского
высшего технического училища было образовано Расчетно-испытательное бюро под
председательством Н. Е. Жуковского. Из этого бюро 1 декабря 1918 г. согласно
постановлению Совета Народных Комиссаров был создан Центральный аэро-гидродинамический
институт (ЦАГИ), объединивший группу учеников Н. Е. Жуковского по Московскому
высшему техническому училищу. Это были В. П. Ветчинкин, А. Н. Туполев, Б. Н.
Юрьев, Б. С, Стечкин, Г. X. Сабинин,
К. А. Ушаков, Г. Н. Мусиньянц, Н. И, Иванов и Н. Г.
Ченцов.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
