Главная
Тема 48. Возникновение
принципа относительности
В настоящее время наряду с механикой
Ньютона, выросшей в результате исследования движений планет и взаимодействия тел,
не находящихся в непосредственном соприкосновении, появилась теория
электромагнитного поля, обнимающая электростатику, электродинамику и
электромагнитную теорию света, причем эта новая область по своей математической
разработанности и подтверждении опытом ничуть не уступала Ньютоновой. В каком отношении будут стоять друг к другу эти две
области физического знания? Сможет ли Ньютонова
механика объяснить электромагнитные явления или нет?
Долгое время обе эти новые отрасли физики развивались
равномерно. Новая наука подсказала возможное решение задачи об абсолютно
неподвижной системе отсчета: это эфир, в котором происходят все
электромагнитные колебания. То, что силы взаимодействия между током и магнитом
не являются действующими по одной прямой, можно объяснить наличием между ними
силового поля, играющего роль передаточного механизма между магнитом и током.
Решающее значение здесь принадлежит опыту.
Первым опытом, произведенным в этом направлении, был
следующий: если эфир представляет абсолютно неподвижную систему отсчета, то
нужно установить, каким образом определяется относительно эфира движение
материальных объектов, например Земли, движущейся вокруг Солнца и вместе с
Солнцем. Для этой цели и был произведен в 1880 г. знаменитый опыт Американских
физиков Майкельсона и Морлея. Идею этого опыта можно
разъяснить так.
Для определения скорости моторной лодки в воде или
самолета в воздухе они должны описать некоторый замкнутый контур, длина
которого известна; при этом необходимо знать время, за которое описывается
круг. В спокойной воде или в безветренную погоду искомая скорость определяется
простым делением пройденного пути на время движения. Определим, как изменится
результат, если опыт производится в среде, двигавшейся с некоторой скоростью.
Пусть рассматриваемый контур представляет квадрат ABCD (рис. 43) со стороной d: По его периметру летит самолет,
скорость которого в спокойном воздухе равна с.
Требуется найти время Т
облета, если слева направо дует ветер с постоянной скоростью v.
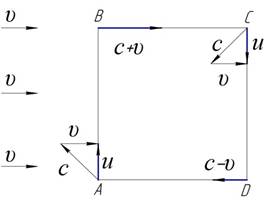
Рис. 43
При полете от А
до В самолету надо брать несколько
влево, чтобы его абсолютная скорость и, равная геометрической сумме v и c
![]()
была
направлена по прямой АВ.
Соответствующее время полета
![]()
При полете от В
до С абсолютная скорость с + v и соответствующее время
![]()
При полете от С
до D самолет впять уклоняется влево,
поэтому скорость опять ![]() , а соответствующее время
, а соответствующее время
![]()
От точки D
до А самолет летит против ветра, его
абсолютная скорость равна с — v и
время полета
![]()
Имеем
![]()

Как видно, отрезки T/
и Т// каждый в отдельности больше времени
полета в спокойном воздухе ![]() , кроме того, время
, кроме того, время

больше времени T/ движения по направлению, перпендикулярному
скорости v.
Опыт Майкельсона был поставлен так: на жесткой
подставке, плававшей в ртути, укреплены источник света S и три зеркала М, М1,
M2 (рис. 44). Свет, идущий от источника S, расщепляется полупрозрачным зеркалом М на два луча: один из них идет к М1 отражается и идет к экрану АА; другой проходит к М2,
отражается в М, еще раз отражается и
идет к АА. Оба отрезка ММ1
и ММ2 равны; если MM1 перпендикулярен к
направлению скорости v Земли в ее
движении вокруг Солнца и со всей Солнечной системой, то время прохождения
отрезка ММ1 вперед и назад
определяется формулой (1), а время прохождения отрезка ММ2 — формулой (2).
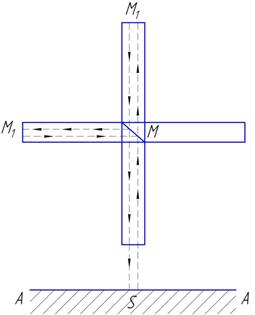
Рис. 44
Так как Т// больше Т/ то оба
луча, пересекаясь на экране, образуют интерференционные полосы. Вращая площадку
вокруг центра и наблюдая за изменением интерференционных полос, Майкельсон
предполагал обнаружить направление и величину скорости Земли по отношению к
эфиру.
Однако в действительности никакого изменения полос не
наблюдалось; все обстояло так, как если бы Земля совершенно не двигалась и
никакого «эфирного ветра» не было, а распространение света по обоим взаимно
перпендикулярным направлениям ММ1
и ММ2 занимало бы
одинаковое время. Для объяснения этого результата было предположено, что
размеры тел по направлению эфирного ветра сокращаются в обратном отношении
времен, а именно
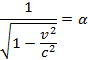
Таким образом, образовались две вполне
сформировавшиеся системы: классическая механика Ньютона, сложившаяся на
основании наблюдений так называемых механических движений, и электродинамика
Максвелла, описывающая совершенно точно течение электромагнитных явлений. Можно
считать, что в области движущихся систем отсчета механические и
электромагнитные процессы ведут себя неодинаково.
Рассмотрим наблюдателя, мимо которого проходит поезд:
если в вагоне этого поезда без начальной скорости падает тяжелое тело, то
наблюдатель увидит это тело движущимся по параболе. Пересадим теперь
наблюдателя на поезд и заставим его смотреть на тело, находящееся на станции и
тоже падающее без начальной скорости; он тоже увидит это тело движущимся по
такой же параболе: происходит действие так называемого закона относительности
Галилея.
Теперь рассмотрим заряженный проводник, рядом с
которым имеется точечный заряд электричества. Если проводник и заряд
неподвижны, то неподвижному наблюдателю может показаться, что проводник
образовал электростатическое поле, действующее на этот заряд. Если наблюдатель
пойдет с некоторой скоростью относительно проводника, то при неподвижных
проводнике и заряде ничего не изменится. Если же наблюдатель неподвижен, а
проводник и заряд двигаются, то согласно закону Максвелла движущийся заряд дает
так называемый конвекционный ток, который действует совершенно так же, как и
обыкновенный электрический ток, но только очень слабый. Так как электрическое
поле сменится теперь электромагнитным, то явления получат совершенно иной
характер, отличный от того, который наблюдался при механических движениях.
Сложение скоростей в механике связано с изменением
систем отсчета: абсолютная скорость равна сумме переносной скорости (подвижной
системы отсчета) и относительной (по отношению к подвижной системе отсчета).
Пусть S1
— неподвижная система отсчета с началом O1;
по ее оси O1X движется с
постоянной скоростью v0
подвижная система отсчета S2
с началом О2, имеющая
форму прямой, скользящей по оси O1x;
по этой прямой движется точка, расстояние от которой до начала O2 равно x2 (относительное движение), а до O1 (абсолютное движение) равно x1. Пусть в начальный момент t = 0 точки O1
и О2 совпадают; тогда
переход от системы S1 к
системе S2 выразится
следующими уравнениями:
![]()
При этом считаем, что время одинаково протекает как в
системе S1 так и в системе
S2; можно выразить это,
если добавить еще одно, четвертое уравнение:
![]()
Приведенные четыре уравнения (так называемые галилеевы
преобразования) заменим другими, которые более правильно описывали бы
совершающиеся события. Основное требование, которому должны удовлетворять новые
уравнения, берем из опыта Майкельсона; он показывает, что во всякой системе
отсчета, движущейся или неподвижной, скорость света должна иметь постоянную
величину с.
В тот момент, когда начала обеих систем S1 и S2 совпадают, пустим из общего начала световой сигнал.
Его движение в обеих системах определим по формулам
![]()
Так как система S2
движется по отношению к S1,
то x1 больше, чем х2; это показывает, что t1 тоже больше, чем t2 поэтому неравенство времен
t1 и t2 в обеих системах является правильным; в движущейся
системе время, а также и все процессы изменения протекают медленнее, чем в
неподвижной.
Если возведем правые и левые части последних двух
уравнений в квадрат, то
![]()
Это тождество соблюдается в обеих системах; ему и
должны удовлетворять формулы преобразования. Так как координаты у и z
остаются неизменными, то достаточно получить лишь формулы для x и t.
Можно потребовать также, чтобы зависимости между х и t
выражались простыми линейными функциями:
![]()
Кроме тождества (а) можно поставить еще и такие
требования:
1) коэффициенты a, b, £, п должны, как и в
галилеевых преобразованиях, зависеть только от относительной скорости v0 обеих систем;
2) при x2
= 0 они должны иметь x1 = vot1.
Последнее условие показывает, что
![]()
откуда
![]()
Теперь формулы принимают вид
![]()
Возведем x2
и t2 в квадрат и подставим
их значения в (а):
![]()
сравнивая в обеих частях коэффициенты при ![]() и
и ![]() получаем
получаем
![]()
![]()
Решая эти уравнения, находим
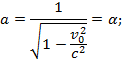
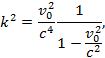
откуда
![]()
и

Уравнения принимают вид
![]() .
.
Если требуется, чтобы t1 и t2
изменялись в одном направлении, то нужно взять нижние знаки:
![]()
Полученные преобразования носят название
преобразований Лоренца.
Обратные преобразования получим, если изменим знак v0:
![]()
Если величина vo
очень мала по сравнению с величиной с,
то эти уравнения принимают вид
![]()
Таким образом, галилеевы преобразования оказываются
частным случаем лоренцовых.
Теперь уже нетрудно объяснить причину отрицательного
результата опыта Майкельсона.
Возьмем уравнение, выражающее x1 через x2
и t2 и положим t2= 0. Тогда
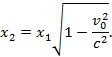
Но x2
— это длина бруска в системе, для которой направление скорости v0 коллинеарно со скоростью
света. Теория относительности дает именно ту величину сокращения бруска, которая
предполагалась Лоренцем для объяснения неудачи опыта Майкельсона.
Равным образом, если в выражении для t1 положим x2 = 0, то получится
замедление времени в движущейся системе:

Рассмотрен случай, когда скорость v0 имеет направление оси Ох. Можно взять и общий случай; тогда тождество (а) получит вид
![]()
Если введем ![]() , то приведенную формулу можно выразить так:
, то приведенную формулу можно выразить так:
![]()
Выражение в левой части очень похоже на квадрат длины
радиуса вектора точки в четырехмерном пространстве, где четвертая координата
имеет выражение ict. Соответствующий
радиус-вектор в таком четырехмерном пространстве носит название четырехвектора.
Последний можно было бы представить в виде кватерниона, если только взять
скалярную часть в виде ict, а
векторную — в виде трех действительных чисел, имеющих направления координатных
осей.
Теперь рассмотрим, как нужно заменить закон сложения
скорости в классической механике.
Пусть переносная скорость равна v0. Координатные оси подвижной системы возьмем так,
чтобы ось Ох2 совпадала с
направлением v0. Пусть
время неподвижной системы координат Ox1y1z1
равно t1 а время подвижной
системы t2 Проекции
относительной скорости на подвижные координатные оси
![]()
проекции
абсолютной скорости
![]()
Дифференцируя уравнения Лоренца
![]()
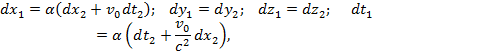
Отсюда
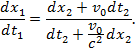
Разделив числитель и знаменатель на dt2 и положив получим ![]() , получим
, получим

Аналогично
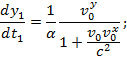
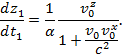
Если vo
очень мало по сравнению со скоростью света с,
то эти формулы переходят в обычные формулы сложения скорости классической
механики:
![]()
Рассмотрим частный случай: ![]() . Имеем:
. Имеем:
![]()
Как видно, скорость материальной частицы по отношению
к любой системе отсчета не может быть больше скорости света. Если в классической
механике увеличение скорости происходит совершенно одинаково, какая бы ни была
величина начальной скорости, то здесь чем больше величина увеличиваемой
скорости, тем труднее её дальнейшее увеличение; оно становится невозможным,
если увеличиваемая скорость равна скорости света. Из этого можно сделать вывод,
что мера инерции материальной точки — ее масса — должна тоже возрастать с
увеличением скорости.
Составим основное уравнение динамики Ньютона — сила
равна произведению массы на ускорение — в двух системах: неподвижной Ox1 и подвижной Ох2:
![]()
Имеем:
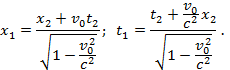
Положив в первом и втором уравнениях соответственно t2 = 0 и x2 = 0, получим:
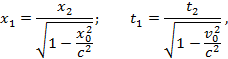
откуда после дифференцирования
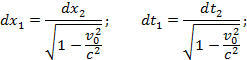

Подставив эти результаты в выражение для силы F, получим:

откуда
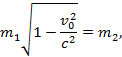
или
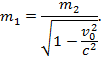
Но т2—величина
массы, которую видит наблюдатель, находящийся в подвижной системе и,
следовательно, считающий ее покоящейся, a m1—
величина массы для наблюдателя, видящего ее движущейся со скоростью v0. Если покоящуюся массу
обозначим т0, то величина т массы, движущейся со скоростью vо, выразится формулой
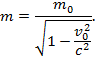
Так как дробь ![]() мала, то эту
формулу можно приближенно представить так:
мала, то эту
формулу можно приближенно представить так:
![]()
или
![]()
кинетическая энергия
Но ![]() —кинетическая
энергия массы m0,
движущейся со скоростью v0
в таком случае увеличение т0
— то массы можно представить в виде
—кинетическая
энергия массы m0,
движущейся со скоростью v0
в таком случае увеличение т0
— то массы можно представить в виде
![]()
Но если увеличение массы равняется энергии, деленной
на квадрат скорости света, то вполне естественно предположить, что величина
покоящейся массы, которую можно выразить как m0— 0, рассчитывается
по такой же формуле
![]()
откуда
![]()
Если масса m0 = 1 г, то
![]()
Не надо, однако, считать, что всю эту массу можно превратить
в энергию; на основании закона сохранения тяжелых частиц (формула закона
сохранения массы) масса покоя остается постоянной и в энергию может только
перейти разность т — т0, но и эта величина
настолько велика, что ее практическое использование вызовет огромную
разрушительную силу.
Как показано выше, в пространстве трех измерений
основной инвариант
![]()
или,
если положить для симметрии ict = u,
![]()
можно
назвать пространственно-временным интервалом между двумя мировыми точками и
строить геометрию этого мира как обыкновенную евклидову геометрий), но только в
пространстве четырех измерений.
В этой геометрии координатные оси были бы прямыми,
двухмерные образы — плоскостями, а трехмерные образы, соответствующие значениям
t1 или u = const, представляли бы обыкновенные
системы трех взаимно перпендикулярных осей со всеми точками, определяемыми при
помощи этих осей. Представить все образы такой геометрии, конечно, нельзя, но
изучать их свойства при помощи аналитической геометрии так же, просто, как и в
обыкновенной трехмерной геометрии. Структуру этого пространства можно разлагать
на прямые, плоскости и трехмерные многообразия. В этом евклидовом пространстве
все будет происходить совершенно так же, как и в обычном; находясь внутри
какой-либо инерционной системы, нельзя заметить ее прямолинейного и
равномерного движения. Но если система, в которой мы находимся, совершает
неинерциальное движение, то можно это заметить, так как тогда появятся так
называемые кориолисовы силы инерции.
Рассматривая знаменитый опыт Ньютона с вращающимся
ведром, наполненным жидкостью, видим, что и Гюйгенс, а в XIX в. и Эрнст Мах
указывали на недоказательность этого опыта для определения абсолютности такого
движения. Возникшая при вращении Земли центробежная сила, обратившая Землю в
сплюснутый эллипсоид вращения, могла иметь своим источником не абсолютное
пространство, а лишь относительное вращение Земли, происходящее по отношению к
системе неподвижных звезд. В 1917 г. Эйнштейн, разрабатывая общий принцип
относительности, писал о том, что в последовательной теории относительности не
может быть никакой инерции относительно пространства, а лишь инерция масс по
отношению друг к другу. Если, следовательно, удалить какую-то массу достаточно
далеко от всех других масс Вселенной, то ее инерция упадет до нуля.
В 1916 г. Эйнштейн формулировал так называемый общий
принцип относительности, касающийся движения и неинерциальных систем.
Основные его положения заключаются в следующем.
Если рассматривается неинерциальное движение, например
человек, поднимающийся с ускорением в лифте, то появляющаяся добавочная
Кориолисова переносная сила инерции не может быть отличима от реальной силы
веса человека. Кориолисова сила инерции обязана своим происхождением инертной
массе человека, а его вес обусловливается гравитационной массой, входящей в
выражение закона всемирного тяготения Ньютона. Но равенство инертной и
гравитационной масс не позволяет отличить силу тяжести от силы инерции:
Кориолисовы силы инерции можно объяснить наличием некоторого силового поля, и
наоборот, силы тяжести можно объяснить соответствующим движением. Из этого
следует, что силы тяжести являются столь же реальными, сколь и Кориолисовы силы
инерции.
Это есть механика Герца, который заменил действующие
силы связями и предположил, что тело будет всегда двигаться по «прямейшему»
направлению.
Движение планет вокруг Солнца можно было бы объяснить
не притяжением их Солнцем, а тем обстоятельством, что геодезическими линиями
вокруг Солнца являются не прямые линии, а конические сечения, которые
появляются вследствие того, что масса Солнца «искривляет» окружающее его
пространство, причем это искривление производится не в трех измерениях, а в
четырехмерном пространственно-временном мире.
Для построения новой механики требуется участие и
неевклидовой геометрии, и вариационных принципов аналитической механики, и
многомерной геометрии и, наконец, общей теории поля, которая могла бы включить
и гравитационное, и электромагнитное, и все другие поля из физики элементарных
частиц.
Таким образом, объем механики необычно расширяется;
она вез более и более стремится слиться с физикой, во всяком случае с ее
теоретической частью; в результате этого слияния рождаются все новые и новые
механики — статистическая, квантовая, волновая, релятивистская, а может быть, и
другие. Из этого, конечно, не следует, что дальнейшее развитие Ньютоновой
механики в строгом смысле этого слова нужно считать исключённым; при изложении
основ теории относительности показано, что Ньютонова механика является
механикой тел, движущихся со скоростями, относительно меньшими скорости света,
а для исследования таких движений современная техника может представить
огромное поле практических приложений.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов