Главная
Тема 4. Кинематика
планетных движений
Важнейшим достижением в истории науки было открытие О.
Нейгебауэром вавилонской математики, а также вавилонской астрономии. Большой
прогресс в математике древности был достигнут примерно в начале второго
тысячелетия до н. э., когда в Двуречьи было образовано объединенное государство
сумеров (так называемая третья династия Ура). В это время была изобретена
шестидесятиричная позиционная система счисления, шестидесятиричные дроби,
аналогичные нашим десятичным, а также решение квадратных уравнений.
Эти открытия сумерийцы сделали на закате своего
исторического существования, так как большинство математических документов
относится к последующему времени, когда столицей этого государства стал Вавилон
и правила в нем семитическая династия. Политическое господство сумерийцев
окончилось, а культурное осталось: шестидесятиричные дроби применялись для
астрономических вычислений в Западной Европе вплоть до времен Коперника (они
даже так и назывались астрономическими); их следы и до сих пор существуют в
наших минутах и секундах и делении окружности на 360 градусов.
Еще больший интерес представляет открытие вавилонской
планетной астрономии. В начале XX в. было довольно распространенным мнение
(берлинская школа Винклера) о чрезвычайной древности вавилонской астрономии.
Считалось, что в Древнем Вавилоне был известен зодиак и его деление на 12
частей — пять летних и семь зимних; отсюда выводилось мистическое значение
числа 7 (семь дней недели, семь тонов гаммы). Большое значение придавалось
прецессии — перемещению точки весеннего равноденствия с Востока на Запад
противоположно видимому движению Солнца. В настоящее время эта точка находится
в созвездии Рыб, в первом тысячелетии до н. э. она находилась в Овне, который и
считался первым знаком зодиака, определявшим начало года.
Возникновение вавилонской науки и философии относилось
к тому времени, когда точка весеннего равноденствия находилась в созвездии
Тельца. Некоторые исследователи относили начала вавилонской культуры еще к
более раннему времени — эпохе Близнецов.
Конечно, в настоящее время вся эта теория представляет
только психологический интерес. Значительно позже появляются так называемые
Omina — приметы или предсказания. Списки этих Omina существовали с очень
древних времен: они касались различных гаданий— по печени, по звездам и др.
Наиболее интересные относятся к VIII—VII в. до н. э.: это донесения придворных
магов и астрологов царям Асаргаддону и Ашурбанипалу. Эти донесения представляют
большой исторический интерес, так как позволяют узнать обратную сторону событий
ассирийской истории; если о победах ассирийских монархов известно из их
торжественных надписей, то о поражениях и других неприятностях можно судить по
тем вопросам, которые цари задавали своим магам. Часто они касались личных дел
царя: спрашивалось, например, выздоровеет ли царь после болезни, как отнесутся
боги к тому, если наследник престола будет назначен соправителем и т. д.; таким
образом, астрологи получали возможность влиять не только на внешнюю, но и на
внутреннюю политику.
Особенный интерес для астрономии представляют тексты,
касающиеся затмений. Например, лунное затмение будет 14 а дара. Когда 14 адара
Луна затмится в первом часу ночи, будет принято решение. Это несчастье для
стран Элама и Сирии, но счастье для царя. Или 15 числа месяца элула Луна была
видна одновременно с Солнцем; затмения не было. Царю написано: будет затмение.
Оно действительно было. Это знамение мира для царя.
Очевидно, предсказания производились на основании
периодов наблюденных затмений. Лунные затмения бывают часто сериями — по
пяти-шести затмений, причем между двумя последовательными затмениями проходил
промежуток времени в шесть лунных месяцев: в начале серии происходило одно-два
частных затмения, в середине — два полных, в конце — одно-два частных. Серии
разделялись промежутками в 17 месяцев без затмений. Такая серийность
наблюдалась, однако, не всегда, но она имела место между 755 — 432 гг. до н.
э.; к этому промежутку относятся упомянутые царствования Асаргаддона и
Ашурбанипала, знаменитое предсказание затмения Фалесом Милетским, а также
упоминаемая в «Альмагесте» эра Набонассара, начало которой падает на 746 год. С
этого года, вероятно, было упорядочено ведение астрономических наблюдений и
хранение ах результатов. Царствования Асаргаддона и Ашурбанипала соответствуют
681 — 625 гг. до н. э., а затмение Фалеса большинство исследователей относят к
585 г. до н. э.
К этому же времени относится записанный около 750 г.
до н. э. в Ассирии большой астрономический текст Mul APIN, представляющий
интерес тем, что в нем впервые появляются зодиакальные созвездия, но как раз не
в качестве знаков зодиака, а в виде так называемых лунных домов. В нем
описываются звезды, которые стоят на пути Сина (Луны): их пределы Син проходит
в течение месяца и оставляет их за собой. Эти звезды имеют такие названия:
Плеяды, Телец, Орион, Персей, Возничий, Близнецы, Рак, Лев, Дева, Весы,
Скорпион, Стрелец, Козерог, Водолей, Западная и Восточная Рыбы, Овен. Из них
возник зодиакальный пояс.
Древних вавилонян интересовало движение Луны за время
полного оборота; движение Луны через эти созвездия они могли наблюдать
непосредственно, чего нельзя сказать о движении Солнца. Зодиакальный пояс они
определили позднее, когда перешли к изучению движения планет, но поскольку
зодиак был известен греку Клеострату Тенедосскому, жившему около 550 г. до н.
э., то можно сказать, что перечень знаков зодиака был составлен примерно около
600 г. до н. э. Нд это указывают новые «божественные» названия планет, которые
через греков и римлян дошли до нас. Планета Венера— Афродита (вавилонская
Иштар) получила свое «божественное» название очень давно, еще при сумерийцах
(III—II тысячелетие до н. э.), когда она вместе с богом Луны Сином и богом
Солнца Шамашем составила божественную троицу. Четыре остальные планеты у
ассирийских астрологов VIII—VII вв. до н. э. носили такие названия: Сатурн
назывался Kaimanu, Юпитер — Mulu Babbar, Марс — Zalbatanu, Меркурий — Bibbu.
Позднее эти планеты получили названия по именам божеств: Юпитер — Мардук
(городской бог Вавилона), Марс —Нергал (бог войны и чумы, городской бог Сиппара
и Куты), Сатурн — Нинурта (бог осеннего Солнца, библейский дикий охотник Немврод,
городской бог Ниппура, древнейшего сумерийского центра), Меркурий — Набу (бог
Борсиппы — предместья Вавилона, бог письма и науки, секретарь Мардука).
То обстоятельство, что самая яркая планета после
Венеры посвящена не Ассуру, верховному богу Ассирии, а городскому богу
Вавилона, показывает, что эти названия появились после возникновения
Нововавилонского царства, расцвет которого приходится на время Навуходоносора
(604—561). Все четыре города, городские боги которых дали имя планетам, были
местами ведения астрономических наблюдений: Вавилон, Борсиппа, Сиппар в
рассматриваемое время, а Ниппур — в древнесумерийское. Иными словами, Ни- нурта
(бог осеннего Солнца) находился к Мардуку (городскому богу Вавилона) примерно в
таком же отношении, как Сатурн —Крон к Юпитеру — Зевсу. Четвертый центр
астрономических наблюдений Урук (от которого тоже имеются астрономические
тексты) имел городского бога Иштар.
Установление периодичности астрономических явлений
было одной из главных задач вавилонской астрономии. Серьезная работа по
определению этих периодов началась примерно со второй половины VI в. до н. э.;
она была необходимой для правильной организации вавилонского лунно-солнечного
календаря.
Известно, что основой вавилонского исчисления времени
был синодический месяц — от одного новолуния до следующего, продолжительность
которого составляла приблизительно 29
суток. Так как
12 синодических месяцев составляли всего лишь 354 дня, а солнечный тропический
год, определяющий распорядок сельскохозяйственных работ, равняется 365
суток, то для
соответствия их надо было иногда вставлять дополнительный 13-й (несчастливый)
месяц. Эти вставки первоначально производились случайно — по велению верховного
жреца или царя, но с VI в. до н. э., или, точнее, с момента образования
персидской монархии, регулировка вставок получала общеимперское значение.
Отношение продолжительностей синодического месяца
(29,531 дня) и тропического года (365,242 дня) можно изобразить непрерывной
дробью и взять от нее ряд подходящих дробей: числители этих дробей представляют
числа лет, а знаменатели — соответствующие числа синодических месяцев:
Первые три соотношения дают очень грубое приближение,
а седьмое и все следующие содержат слишком большое число лет я поэтому
практически совершенно непригодны. Таким образом, нужно рассматривать только
следующие отношения:
К ним можно добавить еще два отношения, полученные в
результате сложения предыдущих и последующих членов рассматриваемых отношений,
а именно
и 
От Нововавилонского царства, а также от эпохи
персидской империи осталось большое количество деловых документов, датированных
годами и месяцами. Вавилонский год начинался с нисана (приблизительно с марта),
а вставной месяц помещался или после 6-го месяца (второй элул) или после 12-го
(второй адар) Так как вавилонский год начинался на три месяца позже нашего, то
обозначим его двумя числами (например, 611 — 610 — начинающийся 1 нисана 611 г.
и заканчивающийся 30 адара 610 г.). Если разделить дату каждого года на число
лет в рассматриваемом цикле, т. е. 8, 11, 19, 27 или 30, и отметить остатки,
соответствующие вставным годам, то получим столько же следующих циклически друг
за другом различных остатков, сколько вставных годов в рассматриваемом цикле
(если вставной месяц был элул, то нужно делить первую дату года — в
вышеприведенном примере 611, а если вставной месяц был адар, то вторую — 610).
Наличие циклических остатков при делении на число лет
в цикле служит признаком того, что данный цикл в действительности и
употреблялся. Оказалось, что для первой половины VI в. до н. з. нельзя
подметить какого-нибудь правильного применения регулирующего цикла вставных
годов; начиная с 544/3 года можно подозревать употребление октаэтериды, которая
исчезает полностью после 527/6 года. Для V в. до н. э. нельзя решить, какой из
циклов был в употреблении: 19-летний или 27-летний, но начиная с 372 г. до н.
э. единственным употреблявшимся циклом был 19-летний, дающий ошибку в один день
только по истечении 11 циклов, или 19×11=209 лет. В еврейском календаре
этот цикл употребляется и в наше время.
Самой ранней из известных сейчас астрономических
вычисленных таблиц была астрономическая афемерида для 523 г. до н. э., определяющая
движение Луны; она интересна в том отношении, что некоторые ее части должны
быть наверняка предвычислены.
Возникает вопрос, какие факторы способствовали
развитию астрономии в VI в. до н. э. Время, протекшее от возвышения Ассирии
(примерно IX в. до н. з.) до возникновения Римской империи (битва при Акции, 30
г. до н. э.), можно определить как время, посвященное процессу объединения
стран, окружающих Средиземное море. Это время соответствовало полному развитию
так называемого железного века, характерными представителями которого являются
ассирийцы и греки, а также рабовладения античного типа.
Государствами-объединителями выступали последовательно
Ассирия (IX—VII вв. до н. э.), Нововавилонское царство (VI в. до н. э.), Персия
(VI—IV вв.), эллинистические государства и Рим. Это объединение не только
положило конец существованию мелких государств Сирии и Двуречья, но и и
произвело чистку божественного пантеона этих стран; народы потеряли веру в
могущество своих племенных божеств, которых считали верховными правителями
своих стран. В VI в. создаются универсальные религии: маздеизм в Иране,
еврейская религия в Палестине, буддизм в Индии, философские системы Конфуция и
Лао-Цзы в Китае. На смену религии приходит наука — начинается изучение
процессов природы; люди перестают верить, что «Зевс дождит», и начинают искать
более естественные объяснения. В Греции создаются философские школы, которые
ищут начала всех вещей в воде (Фалес), в воздухе (Анаксимен), в огне
(Гераклит), но никоим образом не в «матери сырой земле» — краеугольном камне
всех земледельческих религий.
Объединительный процесс сопровождался большими
страданиями народов и пессимистическими настроениями. Особенно обострился этот
процесс, когда после мелких государств были завоеваны мидянами и персами такие
крупные, как Ассирия и Вавилония. Народы начинали искать выхода если не в
настоящем, то по крайней мере в более или менее отдаленном будущем. Жители
Двуречья помещали своих богов на планеты, делая их простыми вестниками фатума —
верховной Судьбы.
Вера в периодичность мировых явлений, прежде всего
небесных, а самое главное — возможность их предсказания, предвычисления
способствовали развитию вычислительной астрономии, которая, таким образом, как
бы оправдывала расцветавшую пышным цветом астрологию; в Двуречье она касалась
только судеб государств, но в Греции, где каждый стремился наиболее ярко
выразить свою индивидуальность, от астрологии начали требовать и предсказания
судеб отдельных личностей. В результате этих смутных стремлений возник один из
краеугольных камней современной науки; если Греция заменила истину откровения
истиной логического доказательства, то вавилонской науке принадлежит честь
установления принципа, что естественноисторические процессы могут быть выражены
математически.
Расцвет вавилонской астрономии, если судить по
количеству дошедших до нас астрономических документов, относится примерно к
промежутку 300—150 гг. до н. э. Методика вавилонских астрономов значительно
отличалась от современной; сейчас рассматривают движение исследуемого светила
как движение некоторой материальной точки; вавилонян же интересовали главным
образом геометрические точки — места, которым соответствовали характерные
положения светил: соединение, противостояние планет, перемещение точек
пересечения орбиты Луны с эклиптикой, восходящий и нисходящий узлы и т. д. Для
этих явлений («фаз») определялись в первую очередь их периоды; особенно хорошо
были изучены периоды движений Луны и Солнца.
Описание движения планеты сводится к описанию
перемещений последовательных фаз планеты. Разность долгот между двумя
последовательными фазами называется синодической дугой. Предположим, что для
каждой' фазы известны синодические дуги и соответствующие им периоды; тогда можно
определить последовательные долготы и времена повторения каждой фазы. Эти пять
фаз составляют такую последовательность:
1) первая видимость (гелиакический восход);
2) первое стояние;
3) оппозиция;
4) второе стояние и
5) последняя видимость (гелиакический заход).
Таким образом, получается календарное описание
движения планеты за весь период времени, по истечении которого повторяется
первоначальная комбинация пяти фаз. Вычисления осложняются тем обстоятельством,
что длины синодических дуг, а также соответствующие времена не остаются
постоянными, а зависят от положения светила на эклиптике. Самый простой способ
учета этих особенностей состоит в том, что эклиптика делится на некоторое число
частей, для каждой из которых определяется величина синодической дуги и время
синодического оборота.
Поскольку вавилоняне интересовались главным образом
астрологической стороной вопроса, то естественно, что его физическая сущность
оставалась нераскрытой. У них нет никаких данных относительно величин и
расстояний небесных светил, хотя им было известно, что видимый диаметр Луны не
всегда одинаков; он изменялся между 34′16″ и
29′27″ (современные значения 32′55″
и 29′30″). Вавилонский жрец Берос, бывший
одним из распространителей вавилонской науки в Греции (вторая половина IV в. до
н. э.), объяснял фазы Луны тем, что одна половина шара Луны является
светящаяся, а другая темная, в то время как правильное объяснение было известно
грекам еще за сто лет до Бероса (Анаксагор).
Однако Берос не был первым, познакомившим греков с достижениями
вавилонской астрономии; вавилонская наука была известна грекам по крайней мере
за полвека до Бероса, т. е. примерно между временами Платона и Аристотеля.
Платон еще употреблял так называемые пифагорейские названия планет: Меркурий
(Стиль- бон), Венера (Фосфор и Геспер), Марс (Пироент), Юпитер (Фаэтон), Сатурн
(Файнон); у Аристотеля же планеты носили названия: звезда Гермеса, звезда
Афродиты, Ареса, Зевса и Крона, — представляющие собой перевод на греческий
язык вавилонских «божественных» названий. Нельзя сказать, что вавилонская
астрология встретила у греков благоприятный прием: Евдокс Книдский определенно
утверждал, что халдейским предсказаниям нельзя верить. Он даже создал
кинематическую картину строения Солнечной системы, заменив детерминизм фатума
законом механических движений.
Деятельность Евдокса относится к первой половине IV в.
до н. э. (примерно 400 — 344 гг. до н. э.). Это — один из величайших греческих
математиков. Он родился на острове Книде, изучал математику у Архита
Тарентского и на 23 году жизни приехал в Афины изучать философию у Платона.
Спартанский царь Агесилай дал ему рекомендацию к египетскому фараону Нектанебу;
в Египте он изучал астрономию в Гелиополе и производил наблюдения в
обсерватории, которая существовала еще в эпоху императора Августа. Затем в
Кизике на Мраморном море он основал математическую и философскую школы.
В области математики Евдоксу принадлежит метод
исчерпания, которым пользовался Архимед при определении площадей и объемов
криволинейных тел. Ему также принадлежит изложенная в 5-й книге Евклида теория
отношений несоизмеримых величин, все значение которой было понято в Европе
только во второй половине XIX в., после работ Дедекинда об иррациональных
числах. Он занимался решением задачи об удвоении куба и в связи с этим произвел
разделение кривых на два класса: сечения и геликоидальные кривые.
Геликоидальными кривыми Евдокс называл некоторые кривые, получающиеся в
результате движения: к числу их относятся спираль Архимеда, квадратриса
Динострата, гиппопеда Евдокса. Венцом его славы является решение задачи,
поставленной Платоном перед астрономами, — каким образом можно объяснить
планетные явления при помощи равномерных упорядоченных круговых движений. Так
была создана первая механическая модель планетных движений, а именно: теория
гомоцентрических сфер.
Согласно этой теории движения небесных светил
получались в результате вращения различных сфер, центр которых совпадал с
центром неподвижной Земли. Исходным было, конечно, суточное вращение небесного
свода, которым греки объясняли движения (восход и заход) неподвижных звезд. Для
Солнца и Луны одного этого вращения уже не было достаточно: требовалось
объяснить видимое перемещение этих светил по отношению к небесному своду.
Отмечая последовательные положения Солнца среди
неподвижных звезд (естественно, что для этого, кроме наблюдений, требовалось и
некоторое вычисление), можно было установить, что Солнце в течение года
описывает большой круг небесного свода, так называемую эклиптику. Это движение
можно было представить, поместив Солнце на некоторую сферу с центром в
неподвижной Земле и заставив эту сферу вращаться с запада на восток вокруг
полюсов эклиптики; при помощи сложения двух этих вращений вполне
удовлетворительно объяснялось видимое движение Солнца. Эклиптика па небесном
своде являлась основной линией, по отношению к которой определялось положение
Луны и других планет.
Аналогично можно было наметить на небесном своде и
траекторию Луны, которая представляла тоже некоторый большой круг сферы,
пересекающийся эклиптикой в так называемых узлах. Если бы эта траектория была
неподвижной по отношению к эклиптике, то движение Луны можно было бы
представить введя третью сферу; полюсы этой сферы находились бы на второй
сфере, на которой начерчена эклиптика. Поместив Луну на этой сфере и заставив
ее вращаться вокруг ее полюса в течение 
дней
(продолжительность сидерического обращения Луны), можно было бы представить
видимое движение Луны.
Но оказалось, что точки пересечения лунной траектории
эклиптикой (узлы) перемещаются по эклиптике приблизительно за 19 лет. Тогда
движение Луны можно было бы объяснить при помощи введения трех сфер: первая,
вращающаяся вокруг полюсов мира, представила бы суточное движение; вокруг
полюсов эклиптики вращалась бы вторая сфера, несшая лунную траекторию, а на
этой сфере помещались бы полюсы третьей сферы, вращение которой определяло
полностью видимое движение Луны. Таким образом, для Луны потребовалось бы
введение трех сфер, для Солнца вполне достаточно двух сфер, но Евдокс ввел еще
третью, как и для Луны.
Если бы планеты равномерно двигались по небесному
своду каждая по своей траектории, то для описания движения каждой такой планеты
хватило бы трех таких сфер. Но движение планет по своим траекториям не является
равномерным: они иногда движутся вперед, стоят на месте и отходят назад. Это
движение можно было бы представить, добавив к движению второй сферы некоторое
гармоническое колебание вокруг неподвижного центра на третьей сфере, но
перемещающегося вместе с ее движением по второй сфере, несущей траекторию
планеты. Это гармоническое колебание на плоскости можно получить при помощи
механизма эллипсографа (карданова движения), или кривошипно-шатунного
механизма, в котором длина кривошипа и шатуна одинаковы. Если прямая Ох представляет траекторию точки, то
колебательное движение точки В около
центра О можно описать при помощи
формулы (рис. 11)
.
Рис.11
Рис.12
Это получалось как результат сложения двух вращений:
одно из них представляет вращение прямой ОАх'
вокруг центра О с угловой скоростью ω
так, что угол хОА равняется ωt второе вращение совершает прямая
АВ вокруг центра А в противоположную сторону с угловой скоростью 2ω так, что
угол ВАх' равняется 2ωt, а угол АВО = ωt; в таком
случае движение точки В описывается вышеприведенной
формулой.
Карданово движение Евдокс употреблял для описания
прямых и обратных движений планеты. Разница была только в том, что их движение
совершалось не на плоскости, а на сферической поверхности, и прямые Ох и ОА
были заменены дугами больших кругов; в этом случае точка В (планета) двигалась бы не по прямой Ох, а по некоторой кривой в виде восьмерки, ветви которой взаимно касались
в точке О, а крайние точки находились
от О на одинаковых расстояниях в ту и
другую сторону.
Пусть Ох —
эклиптика, точка О — среднее
положение планеты, являющееся центром вращения третьей сферы; угловая скорость ω
этого движения соответствует синодическому обороту планеты.
Точка А
является центром вращения четвертой сферы, которое совершается с угловой скоростью
2ω вокруг центра А по отношению
к третьей сфере. Дуга ОА определяет
угол наклона между осями третьей и четвертой сфер (рис. 12).
Предположим, что в начальный момент центры О, А,
В в указанном порядке располагаются
на эклиптике Ох. Точка В соответствует крайнему отклонению от
точки О; если оно известно, то,
поскольку ОА = АВ, легко определим величину дуги а, измеряющей угол между осями
вращения третьей и четвертой сфер. Пусть теперь третья сфера начинает вращаться
вокруг точки О против движения часовой
стрелки с угловой скоростью ω (угол АОх
= ωt), а четвертая сфера —
вокруг точки А в противоположную
сторону с удвоенной скоростью 2ω (угол х'АВ
= 2ωt). Если бы движение происходило
на плоскости, то точка В двигалась бы все время по Ох. В сферическом движении этого не происходит; можно показать, что
планета В окажется ниже эклиптики Ох.
Рассмотрим равнобедренный треугольник ОАВ и из вершины А опустим сферический перпендикуляр АС на основание ОВ. Дуга ОВ представляет сферический радиус-вектор
планеты В, а угол ВОх/ = Θ — сферический полярный угол планеты. Угол ОАВ равен π— 2ωt, а его половина ОАС
= 
— ωt.
Известно, что сумма углов сферического треугольника больше я; в треугольнике ОАС сумма углов равна
Таким образом Θ > 0; это есть так называемый
сферический избыток, измеряющий площадь треугольника. В начальный момент, когда
ОАВ лежит на Ох, площадь треугольника ОАВ
равняется нулю; значит угол Θ равняется нулю и точка В находится на Ох. Когда
угол АОх/ увеличивается,
площадь сферического треугольника ОАВ,
а следовательно, и угол Θ возрастают, и точка В опускается все ниже и ниже под эклиптикой. Когда площадь ОАВ получает максимальную величину, то и
точка В занимает самое низкое положение.
После этого площадь ОАВ уменьшается,
а В приближается к эклиптике. По
истечении четверти периода кривая ОА перпендикулярна
к эклиптике; площадь ОАВ равна нулю и
точка В (планета) оказывается в точке
О. За это время точка В описывает под осью Ох дугу вогнутой кривой (гиппопеда).
Когда угол ωt изменяется от 
до π
(вторая четверть), то точка В,
находясь ниже эклиптики, описывает такую же дугу гиппопеды, симметричную
первой. Через половину периода дуга ОА
оказывается ниже Ох, и гиппопеда
располагается выше эклиптики, занимая положение, симметричное относительно Ох. Таким образом, получаем кривую вроде
восьмерки, но только верхняя и нижняя ветви в средней точке О не пересекаются, а касаются друг друга.
У Скьяпарелли и всех последователей обе ветки пересекались, так что получалась настоящая
восьмерка. Указанное различие в форме гиппопеды объясняется тем, что в
исследованиях Скьяпарелли имеются две ошибки.
То обстоятельство, что в движении по гиппопеде планета
должна отклоняться от эклиптики, заставляло предполагать, что при ее помощи
можно объяснить отклонения планеты по широте.
В действительности методика вычисления отклонений по широте
была создана только во II в. н. э. Птолемеем. Во времена Евдокса лишь одни
вавилоняне занимались изучением движения но широте, и то лишь одной Луны; для
других планет рассматривались только движения по долготе — единственное, что
было нужно для составления предсказаний, и гиппопеда служила только для более точного
определения движения планеты по долготе.
Кроме того, Скьяпарелли считал также, что положение
планеты на четвертой сфере должно обязательно быть на ее экваторе, иными словами,
дуга АВ должна обязательно равняться
90°; ни у Аристотеля, ни у Симпликия (источников Скьяпарелли) об этом (во всяком
случае достаточно ясно) не говорится.
Таким образом, движение планеты определяется четырьмя сферами:
первая — сфера неподвижных звезд — перемещает начерченную на ней траекторию планеты,
вторая с периодом сидерического обращения описывает среднее движение (изменение
долготы) планеты, а третья и четвертая объясняют прямые и обратные движения.
В систему Евдокса входили шесть сфер для Луны и
Солнца, 20 для пяти планет и одна для неподвижных звезд. Движения всех этих
сфер Евдокс считал независимыми друг от друга, иными словами, его система была
простой кинематической. Позднее ученик Евдокса Каллипп объединил все эти сферы
в единую систему, введя некоторые дополнительные сферы, но не изменяя общего
принципа движения всей системы. Эта система получила одобрение Аристотеля и
поэтому вместе с его философией признавалась вплоть до эпохи Коперника.
Можно задать вопрос: в какой мере система Евдокса
могла удовлетворить наблюдаемым движениям? Так как центром всех сфер была
Земля, то яркость планеты должна быть все время одинаковой, что совершенно не
характерно для Марса и Венеры, так как именно у этих планет замечаются большие
различия в яркости. Поэтому уже в ближайшее после Евдокса время появились
другие теории планетных движений. Первая из них была предложена учеником
Платона Гераклидом Понтийским, который, исходя из того, что планеты Меркурий и
Венера не могут удаляться от Солнца на любое расстояние, предположил, что обе
эти так называемые нижние планеты движутся вокруг Солнца, чем объясняются также
и различия в блеске Венеры. Эта теория Гераклида была общепринятой вплоть до
эпохи Птолемея и даже немного позже; последнее упоминание о ней (уже без имени
Гераклида) встречается у писателя V в. н. э. Макробия. Кроме того, Гераклиду
принадлежит также объяснение суточного движения небесного свода вращением Земли
вокруг своей оси.
Сложнее обстоит дело с объяснением видимого движения
Марса, у которого эпохи наибольшего блеска совпадают с временами противостояний,
т. е. соответствуют положениям, когда планета занимает на зодиаке место, прямо
противоположное Солнцу. В этом случае наиболее близкая к Земле точка орбиты
этой планеты находится в направлении, прямо противоположном Солнцу. Это значит,
что центр кругового движения планеты помещен вне Земли; таким образом появилось
понятие о так называемом эксцентре.
Пусть Т —
место Земли в центре мира, а круг QR
представляет эксцентрический круг, имеющий центр в точке О (рис. 13). Если через Т
и О провести диаметр QR, то точка
Рис.13 Рис.14
Q
будет, очевидно, соответствовать минимальному расстоянию от Земли, или так называемому
перигею, в противостояниях Q Марс находится в направлении, противоположном
Солнцу. Противостояния Марса возможны в любых созвездиях зодиака: это значит,
что направление минимального расстояния TQ
не является постоянным, иными словами, диаметр RQ эксцентра должен вращаться вокруг неподвижной точки Т, причем перигейная точка Q остается всегда противоположной Солнцу.
Одновременно вокруг Земли должен вращаться и центр О эксцентра, а
следовательно, и весь эксцентр.
Так как направление от Т к О всегда совпадает с
направлением к Солнцу, то можно предположить, что центр О совпадает с центром Солнца, тем более, что круговращение вокруг
идеальных геометрических точек в те времена не считалось возможным
рассматривать. Поэтому естественно предположить, что Марс, как и Венера с
Меркурием, совершает круговое обращение вокруг Солнца; то же самое можно
применить и к остальным верхним планетам — Юпитеру и Сатурну. Получается
система, которую во второй воловине XVI в. предложил датский астроном Тихо
Браге; все планеты вращаются вокруг Солнца, а Солнце в свою очередь вращается
вокруг Земли.
Если рассмотреть и систему Гераклида Понтийского для
Венеры и Меркурия, то, кроме эксцентра, получим еще одну модель планетных
движений (рис. 14) — эпицикл PS, по
которому движется нижняя планета вокруг Солнца О. Оба понятия — эксцентр и эпицикл— встречаются впервые у младшего
современника Архимеда, Аполлония Пергского, автора «Конических сечений».
Окружность, по которой перемещается центр О эпицикла, носит название деферента.
Аполлоний показал, что движение любой планеты можно получить при помощи как
первой, так и второй модели. С точки зрения кинематики это равносильно движениям
шарнирного параллелограмма.
Пусть О (рис. 15) — неподвижная точка, S — планета, движение которой следует
описать. Это можно сделать при помощи подвижного эксцентра, радиус которого AS, а центр А, а также при помощи эпицикла радиусом BS и центром В; все будет
зависеть только от порядка, в котором складываются вращения: порядок ω1
→ ω2 соответствует модели эксцентра, а порядок ω2
→ ω1 модели эпицикла.
Рис.15
Рассмотрим опять рис. 13, изображавший модель
подвижного эксцентра, где планета (Марс) вращалась вокруг Солнца О, а Солнце — вокруг Земли Т. Из этих двух точек Т и О
неподвижной являлась точка Т, а также
орбита ОО' Солнца. В качестве неподвижной
можно взять и точку О; тогда Земля
будет описывать окружность TТ' вокруг
центра О, а эксцентр QR представит неподвижную орбиту Марса
вокруг Солнца. Кинематически обе системы вполне эквивалентны, но вторая система
получает название системы Аристарха Самосского.
Кто придумал обе кинематические системы? Что касается эпицикла,
то с полной уверенностью можно утверждать, что его автором является Гераклид
Понтийский. Скьяпарелли считал, что систему эксцентра мог придумать современник
Гераклида или даже сам Гераклид; во всяком случае эта система была изобретена
не позже Аристарха. Можно предположить, что ее создал сам Аристарх. Этот
великий астроном древности написал сочинение «Об определении величин и
расстояний Солнца, Луны и Земли». Так как лунные затмения происходят в то
время, когда Земля находится на одной линии с Солнцем и Луной, то Луна попадает
в тень, отбрасываемую Землей. Проведем конус общих касательных к сферам Солнца
и Земли и определим, с какой стороны будет находиться вершина этого конуса.
Зная продолжительность полного затмение, можно вычислить величину диаметра
земной тени на расстоянии Луны; он оказывается меньше диаметра Земли. Это
значит, что вершина конуса земной тени лежит в той же стороне от Земли, что и
Луна; следовательно, диаметр Солнца больше диаметра Земли. Это и было
установлено Аристархом в названном выше сочинении; причем из текста этого сочинения
можно установить, что во время его написания Аристарх придерживался еще
геоцентрических воззрений. Но если диаметр Солнца больше диаметра Земли по Аристарху
примерно в семь раз, то это значит, что объем Солнца в 343 раза больше объема Земли;
тогда из двух возможных предположений — геоцентрической и гелиоцентрической
системы — наиболее вероятным является второе, которое и было принято Аристархом.
В таком случае возникает естественный вопрос: почему
же гелиоцентрическая система Аристарха была отброшена в процессе развития
астрономии? Обычное объяснение заключается в том, что Аристарха постигла та же
судьба, что и Галилея. Глава стоиков Клеанф предъявил ему обвинение в безбожии
за то, что он сдвинул с места очаг (Гестию) Вселенной. Для характеристики
воззрений стоиков служит теория Фатума, подкрепленная астрономическими или,
точнее, астрологическими теориями вавилонских астрономов. Действительно,
римское завоевание произвело в греческом мире те же самые пессимистические
воззрения, что и в Вавилоне VII—VI вв. до н. э. В эпоху Клеанфа положение, по
крайней мере в отношении Рима, еще не было угрожающим по сравнению с тем, что
настало во II в. до н. э.; кроме того, более вероятно, что Клеанф удовольствовался
написанием книги «Против Аристарха», о которой в «Жизнеописаниях философов»
упоминает Диоген Лаэртский.
Но были и другие факторы, которые не позволили теории
Аристарха получить общее признание. Ее основными положениями были два
следующих:
1) все планеты должны вращаться вокруг центрального
материального тела;
2) эти круговые вращения должны быть равномерными.
Оказалось, что оба положения Аристарха были
несовместимыми. Нельзя было доказать, что вращение Солнца вокруг Земли или
Земли вокруг Солнца является равномерным.
Еще до Евдокса греческие астрономы Метон и Евктемон
показали, что продолжительность астрономических времен года, т. е. промежутков
от равноденствий до солнцестояний, не одинакова; после же Аристарха эта
неравномерность стала очевидным и общепризнанным фактом. Если признать, что
небесные движения являются круговыми и равномерными, то нужно было отвергнуть
его первое положение, а именно: считать, что центром вращения должно быть
материальное тело.
Через сто лет после Аристарха никейский астроном
Гиппарх разработал теорию движения Солнца. По этой теории Солнце обращается не
вокруг Земли, а вокруг центра некоторого круга, эксцентрического по отношению к
Земле — так называемого неподвижного эксцентра.
Рассуждения Гиппарха сводились к следующему (рис. 16).
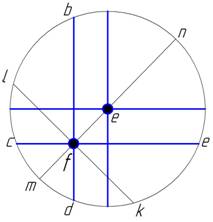
Рис.16
Пусть от весеннего равноденствия до солнцестояния
проходит 
дня, а от
солнцестояния до осеннего равноденствия — 
дня; среднее
равномерное движение в первом промежутке 93°9', а во втором 91°10'. Построим
круг с центром е отложим дуги аb = 93°9' и bс = 91°10' и проведем взаимно перпендикулярные прямые ас и bd,
пересекающиеся в точке f. Будем
считать, что в точке f находится
Земля, в точке а — Солнце в момент весеннего
равноденствия, в b — оно же в момент
летнего солнцестояния, и в c — в
момент осеннего равноденствия. Определим положение е — центра эксцентрического круга; соединив f с е, получим линию апсид пт.
Точка п будет апогеем, а т — перигеем. Движение Солнца —
равномерное вокруг е — не будет
казаться равномерным из f.
Линию апсид тп
первоначально считали неизменной (отсюда и название «неподвижный эксцентр»), но
арабские астрономы показали, что линия апсид перемещается. Если через f проведем прямую, перпендикулярную к тп, то на дуге knl движение будет более медленным, чем среднее, а на lmk — более быстрым; вблизи точек k и l
дневное перемещение Солнца равно среднему.
Таким образом, в механику вошло понятие о
неравномерном движении. Общий метод исследования движения планеты был следующий:
сначала определялось среднее движение планеты по долготе, а затем к нему
прибавлялись два неравенства, или, как их называли греки, аномалии. Первым
неравенством было так называемое «неравенство по отношению к Солнцу»; оно
происходило от того, что наблюдения производились с Земли, движущейся вокруг Солнца;
это неравенство исправлялось при помощи эпицикла. Второе неравенство, обусловленное
неравномерностью движения планеты по орбите, называлось «неравенством в
отношении зодиака» и исправлялось при помощи эксцентра, как показано выше.
Эта методика вместе с теорией движения планет была
создана во II в. н. э. александрийским астрономом Клавдием Птолемеем (Гиппарх
ограничился только теорией движения Солнца). В эпоху Птолемея уже произошло
полное развитие астрологии, которая повлияла и на астрономию Птолемея. В
средние века вплоть до Коперника его книга, носившая арабизированное название «Альмагест—
Величайший», оценивалась как одно из самых больших достижений астрономии.
После Коперника стали критиковать Птолемея, прежде
всего за его геоцентризм. С другой стороны, защитники Птолемея считали ряд
астрологических сочинений, носящих его имя (Четверокнижие — Tetrabyblon и др.),
ему не принадлежащими. Астрологизм Птолемея совершенно несомненен, даже если
ограничиться одним только «Альмагестом». Он отвергает суточное вращение Земли, причем
сама обстоятельность его критики показывает, что в его время эта теория была
довольно распространенной; он считает, что Меркурий и Венера вращаются вокруг
Земли, хотя с чисто конструктивной стороны это представляло порядочные
неудобства (эпицикл Венеры получался очень большим); в теории затмений он наблюдает,
с какой стороны Луна начинала затмеваться, указывая, что это имело большое
значение для предсказаний.
Вся теория движения Солнца им изложена по Гиппарху,
что видно хотя бы из довольно значительного количества наблюдений, произведенных
в Родосе, где одно время работал Гиппарх. Что же касается теории движения
планет, то она представляет собственное создание Птолемея, в особенности теории
движений планет по широте, которая до него не затрагивалась даже вавилонскими астрономами.
Его критикуют за сделанную им ошибку в 4—5° при определении положения солнечных
апсид, но поскольку это определение основывалось на величинах продолжительностей
времен года, которые давались с точностью лишь до половины дня, то получение хороших
результатов могло быть обусловлено только случайностью.
Общенаучная ценность «Альмагеста» заключается в
методике его исследований движения планеты. Прежде всего делается выбор модели:
эксцентр, эпицикл один или несколько; затем из потребного числа наблюдений
определяются геометрические параметры орбиты, на их основе вычисляется
последовательность положений планеты и результаты сверяются с наблюдениями.
Такая методика характерна для всех физико-математических наук — могут изменяться
лишь гипотезы и предположения.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
