Главная
Тема 5. Эллинистическая
механика. Машины. Золотое правило механики
В
эллинистическую эпоху (330—300 гг. до н. э.) и в последующую за ней эпоху
Римской империи уже не встречается крупных теоретических или философских
обобщений. В области науки, и в частности в механике, имеются приложения на
практике результатов, полученных в предшествующую классическую эпоху.
Появляются большие энциклопедические сочинения, охватывающие всю механику, или
популярные сборники, содержащие различные более или менее «интересные вопросы»;
такова большая серия «Проблем» (к их числу относятся дошедшие до нас в виде отдельного
сборника «Механические проблемы»). Кроме того, имеется большое число
специальной военной литературы, описывающей конструкцию военных машин.
Первым автором
общей механики является Филон Византийский (около 270 — 220 гг. до н. э.), курс
которой состоял из девяти книг. Первая книга, посвященная чистой механике,
представляла общее введение; во второй излагалось учение о рычаге; содержание обеих
этих книг можно восстановить по недавно найденной механике Герона
Александрийского. Третья книга была посвящена устройству гаваней, а в четвертой
(Belopoica) рассматривалась конструкция метательных орудий; она сохранилась
полностью. Отметим замечание автора, что «орудия должны быть красивыми». Пятая
и шестая книги были посвящены пневматике и построению автоматов; их содержание
можно восстановить по соответствующим книгам Герона. Седьмая и восьмая книги
(из которых сохранились большие отрывки) были посвящены защите и осаде городов.
Последняя, девятая книга (смесь) трактовала и вопросы тайнописи.
Содержание
этих книг позволяет узнать интересы и содержание античной техники: военное дело,
городское строительство, торговля и забавы — вот что было основными предметами
занятий античного мира. На первом месте стояло военное дело; именно ему были
посвящены дошедшие до нас части сочинения Филона. Затем шли книги, посвященные
устройству автоматов и пневматических игрушек.
Примерно такой
же характер носила и прикладная механика арабов с тем лишь отличием, что не
имеется книг о баллистах и катапультах: арабская осадная «артиллерия» строилась
на принципе пращи с использованием центробежной силы.
Вторым автором
был талантливый энциклопедист Герон
Александрийский, Он был настолько всеобъемлющим автором, что время его
деятельности относилось к периоду от III в. до н. э. до I в. н. э. Он занимался
практикой вычислений (недавно найдена «Метрика», в которой описано, каким
образом в древности извлекались квадратные корни), элементами геометрии,
теорией измерений (первая книга «О диоптрах», в которой описывался прибор для
счета оборотов колес экипажа), общей механикой (три книги которой имеются в
арабском переводе), военной механикой, автоматикой и пневматикой, а также
оптикой. В «Пневматике» описывается «эолипил», основанный на принципе действия
активной турбины. В «Метрике» находится знаменитая формула Герона для площади
треугольника; недавние исследования показали, что эта формула была получена
Архимедом.
Слава Герона
была настолько велика, что книги с его именем имелись даже в византийскую эпоху
(некоторые ученые даже предполагали существование Герона Младшего).
Время его
деятельности было установлено очень недавно: профессор Нейгебауэр показал, что
солнечное затмение, о котором упоминается в его книге «О диоптрах», было
вероятно в 62 г. н. э., кроме того, в комментариях Евтокия к Архимеду
упоминается книга Герона «Camarica» («О сводах»). Так как сирийская сводчатая
архитектура проникла в Рим в начале II в. н. э. (перестройка Аполлодором
пантеона Агриппы в Риме), то время деятельности Герона можно считать примерно
около 100 г. н. э.
Наконец,
необходимо рассмотреть еще одно произведение, время составления которого тоже
не является вполне установленным: это приписываемое Аристотелю сочинение под
названием «Механические проблемы». Не может быть сомнения в том, что это
произведение вышло из школы Аристотеля, но основанная Аристотелем философская
школа (так называемый Ликей) не была особенно долговечной.
После смерти
Аристотеля его преемником был Теофраст (322 — 287 гг. до н. э.), затем Стратон
Лампсакский (287 — 269 гг. до н. э.) —наиболее самостоятельный из последователей
Аристотеля, получивший прозвище физика (известный французский историк науки
Поль Таннери именно ему приписывает составление «Механических проблем»). При
его преемнике Ликоне начинается упадок; аристотелизм теряет силу и вытесняется
стоицизмом и эпикурейством; школа Аристотеля «засыпает на два столетия».
Возрождение
аристотелизма начинается после находки в Афинах собрания его сочинений, которые
в качестве военной добычи были перевезены Суллой в Рим и изданы одиннадцатым
преемником Аристотеля Андроником Родосским, стоявшим в главе школы в 65 — 50
гг. до н. э. После этого начинается возрождение интереса к аристотелевой
философии, особенно усилившееся ва время Августа, консервативные стремления
которого привели к восстановлению классицизма эпохи расцвета Афин за счет
эллинистической литературы.
Наиболее ярким
представителем нового аристотелизма был Александр
Афродизский (вторая половина II в. н. э.), заслуживший титул
«Комментатора». К этому времени можно отнести составление им сборника
«Problemata» («Задачи»), помещаемого в полных собраниях сочинений Аристотеля,
но никоим образом не могущего ему принадлежать. Этот сборник состоит из ряда
вопросов, относящихся к самым различным отраслям науки и философии; «Механические
проблемы» разделяются на 35 глав (параграфов), каждая из которых содержит
вопрос вместе с ответом. Большая часть этих вопросов касается теории рычага, но
далеко не все из них получают ответ, который можно назвать правильным. Приведем
несколько примеров (параграфов) из этого сочинения.
§ IV. По какой
причине больше всех движут корабль гребцы, находящиеся в его середине?
— Может быть
потому, что весло является рычагом; действительно» опорой будет уключина (ибо
она неподвижна), подымаемым грузом — вода, которое весло отталкивает, а
движущим рычагом матрос. Более длинные части весел находятся в середине корабля
внутри.
§ V По какой
причине небольшое кормило, находящееся на самом конце судна, обладает такой
мощностью, что при действии небольшой рукоятки силой одного человека и без
напряжения приводятся в движение большие громады судов?
— Может быть
потому, что кормило является рычагом, которым действует кормчий, опора
получается там, где кормило прикрепляется к судну, оно же будет рычагом, море —
поднимаемым грузом, а кормчий — движущим.
§ VI. По какой
причине с увеличением высоты рей судно при тех же парусе и ветре будет плыть
быстрее?
— Может быть
потому, что мачта становится рычагом, скамья, в которой она закреплена, —
опорой, судно — тяжестью, которую нужно привести в движение, а двигателем —
ветер в парусе. '
§ XVI По какой
причине древко становится слабее при увеличении его длины и больше изгибается
при подъеме даже, если древко короткое (например; в два локтя) было бы тонким,
а длинное — в сто локтей — толстым?
— Может быть
потому, что при подъеме начало древка, за которое держится рука, становится
чем-то вроде опоры, а конец древка — грузом. Таким образом, чем больше та
часть, которая начинается от опоры, тем по необходимости будет больше и изгиб.
§ XVII. По
какой причине при помощи небольшого клина получается сильное давление и
раздвигаются большие массы?
— Может быть
потому, что клин представляет два рычага, которые противоположны друг другу;
каждый имеет и груз и опору, которую он разрывает.
§ XIX. По
какой причине, если на дерево наложить большой топор с большим грузом, дерево
не разделится? Если же, подняв топор, ударить им дерево, то оно рассечется,
хотя бы ударяющее тело имело значительно меньший вес, чем груз, наложенный на
дерево и действующий только давлением.
— Может быть
потому, что все приводится в действие движением и тяжелое тело лучше
воспринимает движение от веса, двигаясь само, а не покоясь.
§ XXXII. По
какой причине прекращается движение брошенных тел?
— Может быть
потому, что иссякает бросившая сила или же вследствие противодействия, или же
«вследствие стремления книзу, если последнее больше бросившей силы?
§ XXXIII. По
какой причине какое-нибудь тело движется не свойственным ему движением, если
движущее его тело не следует за ним и не толкает его?
— Может быть
это движущее тело первым толкнуло другое, а то, в свою очередь, следующее;
движение прекращается, когда проталкивающее тело уже не в состоянии заставить
движущее тело толкнуть дальше и когда тяжесть движущегося имеет книзу большее
стремление, чем направленная вперед толкающая сила.
Задачи из §
XXXII и XXXIII интересны в том отношении, что они позволяют составить некоторое
представление о том, как автор понимал современную ему динамику.
Читая § XIX,
можно вспомнить известное деление Лейбница сил на живые, действующие движением,
и мертвые — чисто статические.
Такое же,
только еще более ясно выраженное представление имеется и в § XXXII «Иссякание
бросившей силы» напоминает эллинистическое представление о движущей силе как о
чем-то находящемся в самом движущемся теле. Это противоречит подлинному
представлению Аристотеля, который причину движения — силу искал вне движущегося
тела. Аристотелевское представление о силе, следующей за движущимся телом и
находящейся с ним в непрерывном соприкосновении (так называемая теория
антиперистасиса), отражено в § XXXIII, но уже в ответе «может быть» показывает,
что автор не считал такое объяснение обязательным.
Эти
рассуждения показывают, что «Механические проблемы» могли быть написаны только
во второй период развития аристотелевской философии. Можно даже пойти немного
дальше; постараемся найти близкие места в других книгах.
Классическим
автором в области теории архитектуры является Витрувий, живший в I в. до н. э. и служивший у Юлия Цезаря и Августа.
В его произведении «Десять книг по архитектуре» девятая книга отведена
изложению механики; в ней рассматриваются машины разного рода: подъемные,
гидравлические и военные. В третьей главе, посвященной рычагу, приводится такой
пример.
Кормчий
огромного грузового судна, держа валик рулевого весла, двигая его одной рукой
вокруг центра и орудуя им искусными нажимами, поворачивает судно, нагруженное
огромной и непомерной тяжестью товаров и съестных припасов. И, когда паруса натянуты
на середине мачты, корабль не может бежать быстро; когда же реи подняты на
самую вершину мачты, тогда он идет болee стремительным ходом, потому что паруса
набирают ветер не у пяты мачты, служащей центром, а на вершине, далеко отступая
от него.
По существу,
эта та же мысль, что содержится в § V и VI «Механических проблем», даже
совпадает последовательность. Различие заключается в том, что у Витрувия дается
правильное объяснение, у автора же «Механических проблем» — нет. Это исключает возможность
заимствования Витрувием «аристотелевского» текста; оба автора пользовались
каким-то общим источником.
Следы этого
источника можно найти и в «Механике» Герона, во второй книге которой имеются 17
задач того же типа, что и в «Механических проблемах».
Седьмая задача
у Герона формулируется приблизительно так: почему дерево можно разломать
скорее, если нажать на него посредине коленом? (Ср.: «Механические проблемы», §
IV.)
Восьмая задача
у Герона: почему кусок дерева тем слабее, чем длиннее, и почему его изгиб увеличивается,
если его закрепить в одном из его концов? Это уже цитированный выше § XVI.
Девятая задача
у Герона (почему при вытаскивании зубов пользуются щипцами, а не рукой?)
повторяет § XXI из «Механических проблем».
Двенадцатая
задача у Герона (почему находящиеся на морском берегу камни значительной
величины по большей части круглы?) аналогична § XV «Механических проблем», но
ответ у Герона гораздо проще — потому что они были первоначально остроконечными,
вследствие же движения моря один наталкивался на другой, так что острые их
концы вследствие слабости обломились.
В
«Механических проблемах» ответ гораздо запутаннее: может быть потому, что при
движении быстрее перемещается более удаленное от середины. Тогда середина
делается центром, а расстояния— радиусами. Но в одном и том же движении больший
радиус описывает и больший круг. Быстрее движется то, что в одно и то же время
проходит больше, а что на одном и том же радиусе движется быстрее, то сильнее и
ударяет. Таким образом, необходимо, чтобы больше сокрушалось то, что дальше
отстоит от середины. А претерпевающее это необходимо становится округлым.
Пятнадцатая
задача у Герона (почему руль, несмотря на то что он очень мал, отклоняет
большие корабли?) является общей и с Витрувием и с автором «Механических
проблем».
Таким образом,
пять задач у Герона из семнадцати являются общими с «Механическими проблемами».
Рассмотрим еще несколько задач (параграфов) из «Механических проблем».
§ П. По какой
причине коромысло весов поднимается после снятия груза с опущенной части, если
веревка прикреплена сверху, а если коромысло подперто снизу, то не поднимается,
а так и остается?
— Может быть
это потому, что веревка является чем-то вроде отвеса, по одну сторону которого
находится поднятая кверху большая часть коромысла. В таком случае необходимо,
чтобы большая часть опускалась вниз до тех пор, пока линия, разделяющая
коромысло пополам, не совпадет с этим отвесом; таким образом, снимаемый груз
был положен на меньшую часть коромысла.
Если же снизу
будет находиться подставка, то произойдет противоположное, ибо при разделении
коромысла отвесом на две части нижняя окажется большей половины коромысла;
поэтому она не подымается, так как поднятая часть будет легче. Следовательно,
по отнятии груза коромысло останется в покое; все произойдет так, как будто накладывается
дополнительный груз, соответствующий избытку нижней половины коромысла над
верхней.
В современной
постановке эта задача сводится к определению устойчивости тела, имеющего одну
неподвижную точку. В рассматриваемом случае дело сводится к тому, будет ли
центр тяжести коромысла выше или ниже точки опоры. Налицо третий случай, когда центр
тяжести совпадает с точкой опоры; то обстоятельство, что в «Механических
проблемах» он не рассматривается, показывает, что понятие о центре тяжести было
не известно. Автор считает, что при равновесии отвесная линия, проведенная
через точку опоры, должна делить тело на равные части. Именно этого
представления держался Посидоний Родосский (I в. до н. э.). В «Механике» Герона
отмечается, что Посидоний, дал физическое определение для понятия о центре
тяжести или момента: центр тяжести, или момента, есть такая точка, при
подвешивании к которой тяжелого тела оно» разделяется на две равные части.
Архимед и его
последователи в механике уточнили это понятие и установили разницу между точкой
привеса и центром тяжести.
Некоторые
исследователи находили у Герона в этом определении доказательство, что понятие
о центре тяжести было установлено еще до Архимеда каким-то стоиком Посидонием.
Теперь
рассмотрим «Механику» Герона — единственный курс, который от древности дошел до
нас полностью, но в арабском переводе. Он разделяется на три книги,
Первая из них
начинается с описания прибора с зубчатыми колесами, при помощи которого
небольшой силой можно поднять большой груз. Начало этой книги в подлиннике
сохранилось в книге 8-й «Математической Библиотеки» Паппа Александрийского; там
она носит специальное название «Барулк». Описывая этот прибор, Герон
рассматривает зубчатые колеса, сцепленные между собой зубцами, которые движутся
в двух противоположных направлениях—одни вправо, а другие влево. Когда колесо
делает пол-оборота, то точки, находящиеся на его окружности, начинают двигаться
в противоположных направлениях. Может, однако, случиться, что точки (обоих
колес), которые должны находиться в противоположных
движениях, идут в одном и том же направлении — обе вверх или обе вниз; это
относится к точкам колес, находящихся вблизи места сцепления, или в
противоположных этому месту сторонах колес.
В
«Механических проблемах» имеется примерно то же, но только философски
уточняется, что начало причинного объяснения всех подобных явлений заключается
в круге. И это совершенно разумно так как нет ничего невозможного, если
что-нибудь чудесное произойдет из еще более чудесного; самым же чудесным является
одновременное прохождение противоположностей; круг же из них и состоит. Поэтому
нет ничего странного в том, что круг является началом всех чудес.
Пользуясь тем,
что круг движется одновременно противоположными движениями, некоторые
устраивают так, что многие круги от одного движения движутся одновременно в
противоположные стороны, как, например, медные и железные колеса, которые люди,
сделавшие их, жертвуют в храмы. Если бы имелось большое число кругов, то они
произвели то же самое от движения одного-единственного круга. Воспользовавшись
этим присущим кругу природным свойством, мастера устраивали приборы, скрывая
первичный двигатель.
Герон
разбирает случаи, когда большие круги движутся быстрее или медленнее, чем
меньшие. Если круги насажены на одной оси, то большие движутся быстрее, чем
меньшие. Если же круги находятся на некотором расстоянии друг от друга, на одном
и том же теле, но не на одной и той же оси, как у повозок со многими колесами,
то меньшие круги движутся быстрее, чем большие, так как их продвижение вперед
одно и то же. Так как при этом меньший круг должен сделать большее число
оборотов, пока большой делает один, то по этой причине меньший круг будет
находиться в более быстром движении.
Из этого можно
заключить, что даже такие механики, как Герон, еще не представляли различия
между угловой и линейной скоростями.
Герон
разбирает парадокс, известный под именем Аристотелева колеса (рис. 17). Иногда
же движение меньших и больших кругов может быть равноскорым, даже если они находятся
на одном и том же центре. Вообразим два круга (рис. 17) прикрепленными к одному
и тому же центру А; пусть линия ВВ' будет касательной к большому кругу.
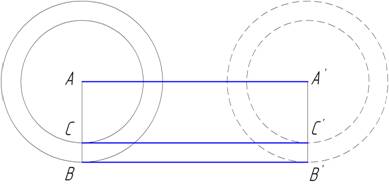
Рис.17
Если соединить
точки А и В прямой, то АВ будет
перпендикулярна к ВВ'; если ВВ' параллельна линии СС', то последняя будет касательной к
малому кругу.
Проведем через
точку А параллельную им линию АА'; если представить большой круг
катящимся по ВВ', то меньший круг будет
катиться по СС'. Когда больший круг
сделает один оборот, то и меньший тоже сделает один оборот, и положение обоих
кругов совпадет с тем, которые имеют два круга с центром в А, а линия АВ займет
положение А'В' и ВВ' будет равна СС'. Но
линия ВВ' представляет расстояние, на
которое прокатится больший круг, сделав один оборот, а СС' будет линией, на которой развертывается меньший круг, делая
один оборот; в таком случае движение малого круга будет равноскорым с движением
большего, так как линия ВВ' равна СС'. Те же тела, которые в равные
времена пробегают равные расстояния, имеют одинаковые скорости и одинаковые движения.
Может
показаться, что это положение противоречит здравому смыслу, поскольку
невозможно, чтобы окружность большого круга равнялась окружности меньшего.
Нельзя утверждать, что окружность малого круга только прокатилась по линии СС'; видно, что вместе с этим меньший
круг прошел путь большего, так что оказывается, что меньший круг достигает
одинаковой скорости с большим при помощи двух движений.
Действительно,
если представить, что больший круг катится, а меньший сидит на точке С неподвижно, то он совершенно так же опишет
линию СС и в то же самое время; тогда и центр А опишет линию АА',
равную ВВ' и СС'. Таким образом, продвижение вперед не будет представлять
развертывания малого круга, ибо видно, что центр А и без качения пройдет то же самое расстояние, благодаря движению,
в котором находится большой круг.
Теория
построения подобных фигур начинается у Герона с решения задачи об удвоении куба
(главы 9 — 12); он описывает построение различных приборов для вычерчивания
подобных фигур — сначала на плоскости (главы 12—16), а затем и телесных (главы 17—19).
Он также описывает нарезку винтовой линии и передачу между плоским зубчатым
колесом и винтом с прямоугольной нарезкой; при этом отмечается, что кроме
прямоугольной может быть и «чечевицеобразная» нарезка.
Рассматривая
вопросы динамики, Герон опровергает мнение о том, что лежащие на Земле грузы
могут быть приведены в движение только равной им силой. Он утверждает, что
помещенные таким образом грузы могут быть приведены в движение силой, меньшей каждой
известной силы, и объясняет причину, почему в действительности такое явление не
наблюдается. Основная идея Герона заключается в том, что между силой и
сопротивлением должен быть строгий закон пропорциональности, причем, если
сопротивление равно нулю, то и сила равна нулю.
Если тело
лежит на горизонтальной плоскости, то оно не имеет склонности двигаться в
какую-либо сторону по горизонтали и потому может быть приведено в движение
сколь угодно малой силой. Если же тело, имеющее вид однородного цилиндра,
находится на наклонной плоскости, то через линию касания можно провести вертикальную
плоскость, которая разделит цилиндр на две части, и находящаяся ниже тяжелая
часть перетянет и сообщит склонность телу двигаться вниз (это представление о
том, что вертикальная плоскость, проведенная через центр тяжести, делит тело на
две равные части). Поэтому груз, который лежит на горизонтальной плоскости, не
имеет склонности двигаться в горизонтальном направлении и потому вследствие
отсутствия сопротивления может быть приведен в движение сколь угодно малой
силой.
Если это не
происходит в действительности, то причиной является трение, но Герон не может рассматривать
его как силу. Он указывает, что вода, находящаяся на слегка наклонной
плоскости, начинает двигаться в сторону наклона; правда, если плоскость не будет
совсем ровной, то в углублениях ее останутся маленькие лужицы; с водой это
получается, так как ее частицы могут легко отделяться друг от друга; с твердым
же телом этого происходить не может; поэтому находящиеся в этих неровностях
части задерживают движение тела, как зубцы в зубчатых колесах.
Герон
рассматривает также вертикальные перемещения грузов: для этого требуется сила,
равная весу подымаемого тела. Если это тело прикрепить к веревке, перекинутой
через неподвижный блок, то для равновесия нужно к свободному концу подвесить
точно такой же груз, но после этого сколь угодно малая перегрузка, добавленная
ко второму грузу, приведет в движение первый груз.
Вопрос о силе
тяжести и о моменте (ϱοπή) подводит к понятию о центре
тяжести, рассмотренному в сочинениях Архимеда. Первая книга механики Герона
заканчивается двумя большими извлечениями из более ранних произведений
Архимеда, а именно из так называемой «Книги опор» (главы 25—31), и затем из
«Книги о рычаге». Интересно представление Архимеда о рычаге, имеющем неправильную
форму.
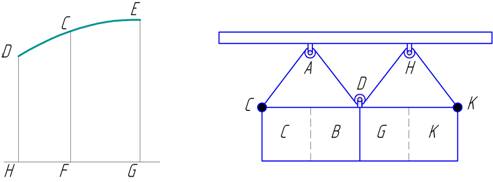
Рис.18 Рис.19
Если С (рис. 18) является точкой опоры такого
рычага, то для получения правильных результатов необходимо, во-первых, чтобы рычаг
находился в равновесии уже до накладывания взвешиваемых грузов в точках D и Е
и, во-вторых, чтобы плечи рассматриваемого рычага измерялись не по расстояниям DC, СЕ
на самом рычаге, а по прямой HG, представляющей
проекцию рычага на горизонтальную плоскость; потенциальными плечами в этом
случае должны быть отрезки HF и FG.
Вторая книга
«Механики» Герона посвящена теории машин, которых он насчитывает пять: ворот,
рычаг, полиспаст, клин и винт. Законы действия первых трех машин ему известны
достаточно хорошо, что же касается клина и винта, то он признает тесное сродство
обеих этих машин, но точного определения законов их действия им не сделано. Он
считает, что «чем острее угол клина, тем легче с ним работать» и что «действие
клина основывается на наносимом ему ударе»; винт же «представляет только
обвитый кругом клин, который, однако, нельзя ударить, но он приводится в
движение при помощи рычага».
Описав машины
(главы 1—6), Герон приступает к наиболее интересной части своего сочинения, а
именно к установлению основного принципа работы машины. Он начинает с
рассмотрения двух концентрических кругов, соединенных вместе и расположенных в вертикальной
плоскости. Два одинаковых груза, подвешенных по обоим концам горизонтального диаметра
большего круга, взаимно уравновешивают друг друга; если один из них переместить
на ближайший к нему конец диаметра меньшего круга, то равновесие нарушится; чтобы
восстановить его, надо, передвинув груз, увеличить в обратном отношении радиусы
обоих кругов. Таким образом, линию, соединяющую точки приложения обоих грузов,
можно рассматривать как коромысло весов, могущих двигаться около неподвижного центра
общих кругов.
Таким образом,
получается, что колоссальную величину можно привести в движение небольшой
силой. Действительно, если около одного и того же центра имеется два круга,
причем больший груз находится на какой-либо дуге малого круга, а меньший — на
дуге большего круга и отношение радиуса большего круга к радиусу меньшего
больше, чем отношение большего груза к малой силе, которая его движет, то малая
сила перевешивает большой груз.
Герон
доказывает, что при употреблении машин подъем грузов происходит медленнее, ибо
«что выигрывается в силе, то теряется во времени». Он разбирает этот принцип
для каждого типа машин. Для объяснения выигрыша в силе для подвижного блока, а
также полиспаста указывается, что вес подымаемого груза распределяется на несколько
веревок (для подвижного блока на две), причем приводится чертеж, который
встречается также и у Леонардо да Винчи (рис. 19). Поднимаемый груз F делится на четыре части: С, В,
G, K, каждая из которых приходится соответственно на веревки СA, AD,
DH, НК. Если веревку НК
отделить от места К прикрепления к грузу
F, то тянувшему за нее человеку нужно
приложить силу, равную натяжению данной веревки, т. е. силу, в четыре раза
меньшую веса груза F. Вследствие
наклонности веревок натяжение будет больше четверти веса, но Герон, может быть,
считал, что все веревки являются вертикальными, и наклонность получилась лишь
для большей ясности чертежа.
Особенно
интересно приводимое Героном объяснение для клина, истинная теория действия которого
оставалась неизвестной античным механикам. В главе 15 он писал (рис. 20), что
всякий удар, даже самый легкий, приводит в движение любой клин. Пусть угол клина
A, а основание — линия DM. Пусть его приводит в движение удар ВС, перемещающий клин на расстояние AD от первоначального положения. Возьмем
от удара ВС некоторую часть — удaр BE, являющийся наименьшим из известных
ударов. Взятый отдельно удар BE
приводит в движение некоторую часть клина.
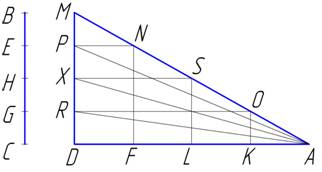
Рис.20
Если удар ВС вызывает перемещение на расстояние AD, то ЕС передвинет клин на расстояние, меньшее AD, положим AF. Добавим
затем удар BE; если перемещение AD производится ударом ВС, то взятый отдельно удар BE даст перемещение
DF. Разделим удар ВС на части, равные
BE, а именно: BE, EH, HG, GС;
тогда и расстояние AD разделится на
части, равные DF, а именно: AK, KL,
LF, FD; таким образом, каждый из ударов BE, EH, HG, GC
произведет соответственно перемещения DF,
FL, LК, KA. Теперь проведем прямые
FN, LS, КО, параллельные DM, а также PN, XS, RO, параллельные AD; тогда получатся равные между собой линии DR, RX, ХР, РМ.
Если полученные точки Р, X, R
соединить с точкой А, то получим
четыре клина с вершинами в А и
основаниями MP, РХ, XR, RD; каждый из них ударом, равным BE, передвигается на расстояние, равное AD.
Таким образом,
если удар BE передвигает весь клин на
расстояние DF = КА, то этот же удар передвинет клин с основанием RD на расстояние AD. Отсюда следует, что отношение ударов BE и ВС соответствует
отношению клиньев DR и DM. То же будет и со временем движения
клина с основанием DR, и с
расстоянием, которое проходит весь клин от удара ВС; все эти отношения будут такими же, как и отношение удара BE ко всему удару ВС. Если вбиваемый клин будет одним из малых клиньев и вбивается
сильным ударом, то он продвинется на столько же, на сколько продвинется весь
клин от совокупности всех ударов, т. е. от целого сильного удара. Так как отношения
времен к временам, ударов к ударам и основания всего клина к основанию каждого
малого клина одинаковы, то получается, что чем меньше угол клина, тем меньше и
сила по отношению к той силе, которая вбивает целый клин.
Основной закон
работы машины Герон формулирует так (глава 22): если при пользовании машиной
требуется увеличение силы, то в результате происходит замедление, ибо чем менее
движущая сила по отношению к движимой тяжести, тем больше потребуется и
времени; таким образом, сила к силе и время ко времени находятся в том же самом
обратном отношении. Это и есть знаменитое золотое правило античной механики: что выигрывается в силе, то теряется в
скорости. Герон проверяет это правило для трех первых видов машин.
Относительно клина и винта он не может выставить того же утверждения, ибо чем
большая сила действует на них, тем меньшим становится каждый из них. Что
замедление имеет место и для них обоих, ясно, поскольку многие удары требуют
больше времени, чем один единственный, и частое поворачивание винта берет больше
времени, чем один оборот.
Таким образом,
доказано, что отношение клинового угла к углу будет обратным отношением
движущего удара к удару. В таком случае и отношение времен является обратным
отношением сил (главы 27 и 28).
Для
характеристики научного кредо Герона большой интерес представляет глава 33
второй книги его «Механики». Он пишет в ней, что занимающимся механической
наукой совершенно необходимо знать причины, действующие в каждом употребляемом движении,
как это и сделано при помощи физических доказательств для каждого вида
разобранных машин, чтобы относительно их не было ничего недоказанного или
вызывающего сомнение, но чтобы при разборе каждой задачи можно было обнаружить
правильность каждого рассуждения.
Тот, кто хочет
основательно узнать все причины, необходимо должен применять естественные
принципы, один или многие, и связывать с ними все, что он исследует; решение
каждого отдельного вопроса дается в основе только тогда, когда отыскана
причина, а последней может быть лишь то, что уже известно.
Вторая книга
«Механики» заканчивается разбором задач древних и практическими задачами на
определение центра тяжести, уже разбиравшимися в главе, посвященной Архимеду
(главы 35—41).
Третья книга
«Механики» Герона трактует о машинах, употреблявшихся в практике того времени,
а именно — о машинах для поднятия тяжестей, а также о прессах различного вида. Представляющая
большой интерес для истории древней техники, она мало что дает по отношению к
теоретической механике.
Примерно то же
самое можно сказать о посвященной механике десятой книге «Архитектуры» Витрувия,
в которой описывается состояние прикладной механики в эпоху около начала нашей
эры.
Приведем
определение машины у Витрувия. Машина
есть сочетание соединенных вместе деревянных частей, обладающее огромными
силами для передвижения тяжестей.
Уже само
определение показывает, что наиболее распространенным типом были грузоподъемные
машины. Кроме них, Витрувий упоминает об «акробатических (верхолазных)
машинах», демонстрирующих «не искусство, а смелость», и о пневматических,
которым у Филона и Герона были посвящены особые книги. Кроме грузоподъемных
Витрувий описывает также и водоподъемные машины (книга X, главы 4—7).
Конец книги X
Витрувий посвящает описанию военной техники. В рассказе Витрувия есть одно
обстоятельство, интересное и для теоретической механики. В главе 16
рассказывается история о некотором архитекторе Каллии, который приехал в Родос,
прочел лекцию и показал модель стены с установленным на ней вращающимся краном,
которым он захватил приближавшийся к укрепление гелепол (буквально «берущая
город» машина) и перетащил его на другую сторону стены. Родосцы пришли в
восторг, отняли
жалованье у старого военного архитектора и передали
его Каллию.
Когда через
некоторое время царь Деметрий Полиоркет осадил Родос и придвинул к его стенам
гелепол, весивший 360 тыс. фунтов, то родосцы потребовали от Каллия, чтобы он
приготовил машину для переноски этого гелепола внутрь стен, но это было
невозможно. Ибо не все возможно произвести одним и тем же способом, но одни вещи,
сделанные по образцу небольшой модели, действуют одинаково и в большом размере,
а для других не может быть модели, но их строят сами по себе; некоторые же
таковы, что на модели они кажутся правдоподобными, но, будучи увеличены,
разваливаются. Буравом можно буравить отверстие в полдюйма, в дюйм и в полтора;
если же таким способом сделать отверстие в пять дюймов, это не было бы
осуществимо, а об отверстии в полфута или больше не приходится даже и думать.
Здесь впервые
отмечается, что между механическим и геометрическим подобиями имеется большая
разница.
Таким образом,
рассмотренные выше три произведения, довольно близкие по духу, характеризуют
механику в том виде, в каком она сложилась в эпоху эллинизма. Деятельность
Витрувия относится примерно к концу I в. до н. э. и началу I в. н. э.
Позднейшие
исследования показали, что время деятельности Герона можно отнести примерно к 100
г. н. э. Время деятельности автора «Механических проблем» все еще не может быть
определено с полной достоверностью, но материал, используемый этим автором и
Героном, имеет очень много общего. Правда, оба писателя отличаются по духу:
чувствуется, что Герон является хорошо образованным специалистом, не признающим
никаких чудес.
Что касается
автора «Механических проблем», то он гораздо более философ, чем специалист; слово
«может быть» в его произведениях встречаются даже в тех случаях, когда
правильный ответ у Герона дается вполне определенно. Принадлежность его к школе
Аристотеля не вызывает никаких сомнений; можно только поставить вопрос: не было
ли у Аристотеля или в его школе сочинения, которое могло быть источником как
для Герона, так и для автора «Механических проблем»? Возможность существования
такого источника нельзя отрицать, но все-таки Герон, цитируя Архимеда и Посидония,
не ссылается на Аристотеля. Он только отмечает «задачи древних», которые
совпадают с некоторым количеством задач в «Механических проблемах»; две из этих
задач встречаются и у Витрувия.
Правда, в
«Механических проблемах» есть два эксцерпта, которые появились до Архимеда: это
параллелограмм скоростей, использованный Архимедом в книге «О спиралях», и
очень интересный эксцерпт о происхождении криволинейного движения в результате
сложения прямолинейных перемещений, «не находящихся между собой ни в каком
отношении». Эта теория вполне может принадлежать если не Евдоксу, то во всяком
случае его школе.
Поэтому можно
предполагать, что «Механические проблемы» содержат некоторый материал,
относящийся ко времени жизни Аристотеля, но этого все же недостаточно, чтобы
приписать их авторство какому-либо исследователю IV в. до н. э. Отнесение
времени жизни автора «Механических проблем» к I и II вв. н. э., т. е. к эпохе
деятельности Герона, в свете всего вышеизложенного является гораздо более
вероятным.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов