Главная
Тема 12. Механика
средневековья. Начало статики. Иордан Неморарий
и Стевин
Крушение Римской империи в IV—V вв. н. э. было
одновременно концом рабовладельческой формации в Средиземноморье, где рабовладение
носило наиболее яркий характер.
У греков рабство имело промышленный, городской
характер; рабы использовались как рабочая сила в мастерских. В Риме положение
было несколько иным: после завоевательных войн III—II вв. до н. э. римляне
получили громадное количество рабов, которых они использовали в качестве
рабочей силы в сельском хозяйстве, в латифундиях богатых патрициев.
Классической страной латифундий был Карфаген, где были
даже написаны специальные сочинения по ведению плантационного хозяйства (Магон), которые были переведены на латинский язык. В Риме
развитие латифундий началось в начале II в. до н. э. после окончания второй
Пунической войны. Период завоевательных войн продолжался и дальше, вплоть до
эпохи Траяна (конец I в, н. э.), завоевавшего Дакию и Месопотамию; от
последнего завоевания его преемник Адриан отказался, и завоевательные войны
окончились.
Но если не было прилива свежей рабочей силы из
военнопленных, то надо было в какой-то степени беречь уже имеющуюся. Во II в.
н. э. появляются законы, запрещающие хозяину убивать
своих
рабов, и в сельском хозяйстве рабы переходят мало-помалу, без какой бы то ни
было «революции» в положение крепостных: начинается феодальная эпоха. В течение
V в. н. э. на развалинах Западной Римской империи возникли «варварские»
государства, и вожди германских дружин заняли места римских патрициев в их
латифундиях. Правда, центр культурной жизни Средиземноморья в течение второй
половины I тысячелетия н. э. лежал совсем не в пределах Западной Европы, а
восточнее — в Византийской империи и Передней Азии.
В пределах Византийской империи сохранилась городская
жизнь и оживленная торговая деятельность; равным образом и в области культуры
жизнь шла гораздо более интенсивно, чем на западе.
II в. н. э. часто называют «греческим возрождением».
Это было своего рода возрождение, но только на греческом языке писали главным
образом не греки; так, наиболее выдающимся писателем II в. был сириец Лукиан Самосатский. Начиная со II в. н. э. развивается сирийская сводчатая архитектура,
хорошо известная по византийским образцам (собор «Святая София»); сирийский
архитектор эпохи Траяна Аполлодор перестраивает
римский Пантеон, имевший первоначальную форму, обычную для всех грекоримских храмов; теперь верхняя часть храма приобретает
форму купола.
В области математики выделяются Никомах
Геразский и Феодосии Триполийский;
даже в такой, казалось бы, специфически римской деятельности сирийцы имеют
юридическую школу в Берите (современный Бейрут), давшую ряд замечательных
юристов (Ульпиан).
Громадное значение сирийцев заключается в том, что они
были передатчиками античной науки арабам. Вершиной их деятельности является VII
и VIII вв. и. э. (первая половина), когда столица Арабского халифата при Омайядах находилась в столице Сирии Дамаске. Около 750 г.
столица халифата перешла в Багдад, и сирийское влияние в арабской науке
сменилось иранским.
Страны Передней Азии не знали сильно развитого
рабовладения античного типа; поэтому на их почве феодализм принял ярко
выраженную форму и был гораздо сильнее, чем в Западной Европе. Отличительный
внешний признак феодализма (гербы) был заимствован в эпоху крестовых походов с
востока; на это указывают названия цветов в геральдике: azur—
синий, gueules (персидск. ghul) — розовый,
В эпоху средневековья, начиная от крестовых походов и
до турецкого завоевания, Запад оставался побежденным в столкновении с Востоком:
даже в XVI в. самыми сильными государствами были империи османов в Европе и
великих моголов в Индии; если с XVI в. начался перелом, то это произошло в значительной
степени благодаря тому, что мировые торговые пути из Средиземноморья перешли
после открытия Америки на берега Атлантического океана.
Очень распространено мнение, что эпоха средневековья
представляет темное время. Это мнение в известной степени справедливо для
Западной Европы, да и то лишь в эпоху раннего средневековья—примерно до XII в.
н. э. Для Востока наблюдается обратное положение—это время блестящего расцвета
Арабо-Иранского халифата на западе Азии и Танской
империи на ее востоке.
В чем заключалось основное отличие между
рабовладельческой и феодальной формациями? В классических странах рабовладения
— грекоримском мире — наиболее характерной являлась
городская жизнь, жизнь «полисов» — греческих, италийских или эллинистических.
В конце античной эпохи городская жизнь в значительной
степени замерла, города сохранили роль главным образом торговых центров; в
хозяйственной области на первом месте выделились крупные земельные владения;
«государство-город» сменился «государством поместьем», рабы сменились
крепостными колонами, вместо городской промышленности на первое место выступило
сельское хозяйство; основную роль начинала играть деревня; вместо окатывающего
большие области городского товарооборота появилось замкнутое в значительной
степени самодовлеющее домашнее хозяйство.
В этом отношении очень интересно сравнить развитие
наук физико-математического и биологического циклов. В то время как между
греческой геометрией, средневековой алгеброй и анализом XVIII в. замечаются
большие различия, «Historia Naturalis»
Плиния и «Естественная история» Бюффона имеют приблизительно одинаковый
характер; «Афоризмы» греческого врача Гиппократа перепечатывались еще в первой
половине XIX в. Если физико-математические науки в значительной степени росли
из самих себя, то успехи биологических наук получались в результате вторжения
постороннего начала: изобретение микроскопа, успехи химии, появление лучей
Рентгена и т. д. Так как в области развития науки стимулирующим фактором
являлся город, а не деревня, то ясно, почему в эпоху феодализма так медленно
развивались точные науки.
Какие слои населения обслуживала средневековая наука?
Ими, конечно, не были широкие массы средневекового крестьянства, задавленного
тяжелой сельскохозяйственной работой и не имевшего ни сил, ни времени, ни
возможностей для повышения своего культурного уровня. Это могли позволить себе
только высшие слои землевладельческого общества, имевшие и досуг, и
материальные средства для удовлетворения своих культурных потребностей. Им
нужны были поэты для восхваления их успехов и услаждения досугов, историки для
оправдания преступлений и медики для исцеления. И средневековье дало великих
поэтов, трудолюбивых историков, замечательных медиков.
Потребность знания будущего в то время, когда
громадное большинство мусульманских династий существовало не более пятидесяти
лет, удовлетворяла вещая наука — астрология. Построенная на основании птолемеевского «Альмагеста», она требовала больших
математических вычислений; под ее сенью переднеазиатские математики, бывшие одновременно
и астрономами, занимались в часы досуга и чистой математикой, которая —
единственная из всех наук средневековья — добилась в своем развитии больших
успехов.
Во времена от Гиппарха до Коперника, а пожалуй, и еще
дальше—вплоть до конца XVIII в. — астрономия была ведущей наукой в области
физико-математических знаний. Она сыграла большую роль и в развитии кинематики
вращательных движений, и в развитии классической динамики.
Теперь рассмотрим, каково было положение «чистой»
механики или ее частей, не зависящих от астрономических теорий.
В этом отношении как арабская, так и
западноевропейская механика опиралась на учение Архимеда — особенно на книги «О
равновесии плоских фигур» и «О плавающих телах». В книге «О равновесии плоских
фигур» Архимед дал математическое доказательство закона рычага, коромысло
которого предполагалось невесомым.
Практика поставила вопрос о равновесии сил на
неравноплечем рычаге, который уже не считался невесомым; решение этой задачи
требовалось для определения веса особо тяжелых тел (десятичные весы и так
называемый безмен). Этой задачей, решение которой в настоящее время доступно
каждому студенту, занимались в то время ученые трех цивилизаций: римской,
переднеазиатской и китайской.
Первое ее решение принадлежит астроному Клавдию
Птолемею, который дал теорию определения веса тел на неравноплечих весах,
описав прибор, который он назвал χαϱίστιον
(безмен). Книга Птолемея известна из переработки арабского астронома и
математика Сабита ибн Курры
(Thabit ibn Qurra), жившего в IX в. н. э. Его сочинение, получившее в
латинском переводе название «Liber Charastonis», давало решение этой задачи при помощи того же
метода, который применял и Архимед.
Известны сочинения на ту же тему в китайской
математике, тоже относящиеся примерно ко второй половине I тысячелетия н. э.,
написанные, очевидно, вполне самостоятельно без какого бы то ни было влияния со
стороны Архимеда, которое так ясно у Сабита ибн Курры, бывшего первым знатоком Архимеда среди
представителей мусульманской науки.
Из второго произведения Архимеда «О плавающих телах»
практики того времени взяли только формулировку закона Архимеда, необходимую
для построения прибора типа современных гидростатических весов для определения
удельного веса твердых и жидких тел. Впервые такой прибор построил Синезий, епископ Кирены, ученик
знаменитой Ипатии, погибшей от рук разъяренных
монахов (около 400 г. н. э.). Этот прибор ювелиры того времени использовали для
той же цели, что и Архимед в эпизоде с золотым венцом царя Гиерона.
У арабов описанию такого прибора и его теории была
посвящена книга «Весы мудрости», написанная ал-Казини
примерно около 1120 г. н. э. Сочинения на ту же тему имеются и в
западноевропейских средневековых рукописях.
Вышеприведенное показывает, что в странах, примыкающих
с запада и востока к Средиземному морю, механика не развивалась в течение всего
первого тысячелетия нашей эры и даже несколько позже. Чтобы двинуть ее развитие
вперед, необходим был толчок. Этот толчок был дан не там, где культура
феодальной эпохи стояла на наивысшем уровне, а, наоборот, там, где феодальный
строй был наиболее слаб, а именно в средневековой Европе, или, точнее, во
Франции в XIII в. н. э.
В эпоху крестовых походов во Франции и Италии, а также
и в Южной Германии происходила так называемая «революция Коммун»— освобождение
городов из-под власти сеньоров. Это было первое выступление буржуазии,
выступление, не бывшее очень победоносным и закончившееся на исходе
средневековья образованием абсолютных монархий.
Но если буржуазия и не добилась власти во всем
государстве, то все же она сумела освободиться от власти феодальных сеньоров.
Город, получивший свободу путем выкупа или путем восстания, в ознаменование
своей свободы строил помещения для выбранного его жителями правительства
(ратуша), сначала небольшие, а затем уже здания значительно больших размеров, в
которых могла бы собираться основная часть населения города, — это был собор.
Назначение средневекового собора довольно сильно
отличалось от современной церкви, находящейся во власти духовенства; в
средневековом соборе духовенству принадлежала лишь более возвышенная часть —
хоры, а все остальное предоставлялось в распоряжение народа, который проводил
здесь свои собрания, слушал театральные представления духовно-нравственного
характера — мистерии и миракли, а в плохую погоду иногда устраивал даже
ярмарки. Для помещения большого количества народа требовалось и большое здание.
Таким образом, во Франции, точнее, на ее севере,
возникла архитектура, получившая название готической. Словом «готический»
назван немецкий шрифт; поэтому довольно часто готическую архитектуру связывают
с Германией. В действительности даже готический шрифт был создан во Франции; он
был излюбленным шрифтом придворных писцов Людовика IX.
Задача получения большого и достаточно светлого здания
решалась средневековыми архитекторами примерно в таких же формах, как и
современные заводские помещения со стрельчатыми фермами, но то, что теперь
делается в железе и бетоне, они должны были делать в камне. Для возможности
возведения такого здания нужно было знать взаимные давления между отдельными
деталями постройки и не утяжелять чрезмерно здания, как это было в
предшествующей романской и сирийско-византийской архитектуре. Обойтись без
сводов было нельзя, но, как известно, решение задачи на равновесие трехшарнирной арки показывает, что чем больше высота замка,
соединяющего обе половины арки, тем меньше будут боковые давления в опорных
шарнирах арки.
Этим объясняется то, что вместо полукруглых сводов
сирийской архитектуры французские зодчие строили высокие стрельчатые своды
исходя из правила archispiguti nоn
dant impulsam contrafortibus — стрельчатые арки не дают напора
контрфорсам. Так назывались боковые опорные фермы, поддерживающие крышу средней
более высокой части здания и делавшие, по выражению Виктора Гюго, готический
собор похожим на животное, скелет которого находится не внутри, а вне его. В
действительности боковой напор существовал (в противном случае контрфорсы были
бы излишни), но он был значительно меньше, чем у полукруглых сводов.
В это время в школе парижского математика Иордана Неморария
(вторая половина XIII в.) была решена задача, с которой не смогли справиться
античные механики, — задача о равновесии на наклонной плоскости.
Хотя наклонная плоскость применялась древними
египтянами для передвижения грузов при постройке высоких зданий и, согласно
Герону Александрийскому, была одной из пяти основных машин древности наравне с
клином и винтом, законы действия ее оставались тайной для древних математиков.
Основной причиной являлось то, что законы трения и
даже представление о трении как о некоторой силе не были известны древним. Их
«силы» были только движущими; кроме того, определение закона движения при
наличии трения даже на горизонтальной плоскости не могло быть получено при
помощи закона простой пропорциональности— чтобы привести тело в движение, нужно
было приложить предварительно некоторую силу, иными словами, при скорости,
равной нулю в момент начала движения, сила могла не равняться нулю. Тем не
менее решение этой задачи не давало покоя греческим математикам.
Вот как решал ее Герон Александрийский. Предположим,
что надо передвинуть груз по наклонной плоскости. Пусть поверхность этой
плоскости, а также прикасающаяся к ней сторона груза гладкие. В этом положении
необходимо приложить с другой стороны силу или подвесить груз и, кроме того,
иметь некоторый излишек силы над грузом, чтобы поднять его вверх.
Для доказательства правильности предложения разберем
случай, когда грузом является некоторый цилиндр (рис. 21). Так как площадь
соприкосновения цилиндра с наклонной плоскостью невелика, го
цилиндр естественно скатится вниз. Вообразим плоскость, которая проходит через
линию соприкосновения цилиндра с наклонной плоскостью и будет перпендикулярна к
ней. Очевидно, что эта плоскость пройдет через ось цилиндра и рассечет его на
две равные части.
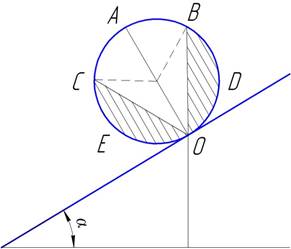
Рис. 21
Через линию соприкосновения цилиндра с наклонной
плоскостью проводим еще вертикальную плоскость. Она делит цилиндр на две
неравные части, меньшая из которых (BOD)
находится в верхней области, а большая (ВСЕО)
— в нижней. Большая часть перевесит меньшую и таким образом цилиндр покатится.
Если с другой стороны вертикальной плоскости отнять
избыток (ОВАС), на который большая
часть превышает меньшую, то обе разделенные части ODB и ОСЕ — окажутся в
равновесии и общий их вес будет неподвижным на линии соприкосновения цилиндра с
наклонной плоскостью; таким образом, этот вес не потянет цилиндр ни вверх, ни
вниз. Поэтому для достижения равновесия требуется сила, равная разности весов
отсеченных частей (т. е. части ОСАВО),
и если теперь к этой силе прибавить маленький добавок, то она пересилит груз.
Правильное решение задачи о равновесии на наклонной
плоскости было дано во второй половине XIII в. французским ученым Иорданом
Неморарием, создателем новой науки — науки о весе (Scientia de ponderibus).
Основная идея Иордана заключалась в установлении различия между весом (pondus —
тот же корень, что и в слове «пуд») тела и его тяжестью (gravitas).
Вес тела, аналогично современному понятию о массе,
имеет постоянную величину; что же касается тяжести — давления или вообще
действия на другие тела, то она может изменяться в зависимости от положения (gravitas
secundum situs). Так, на длинном плече рычага один и тот же вес оказывает
большее давление (имеет большую тяжесть), чем на коротком. Чтобы поднять вверх
свободно висящий груз, нужно приложить силу, равную его весу, но для поднятия
груза по наклонной плоскости нужно приложить силу, которая должна преодолеть не
всю его тяжесть, а только его «тяжесть по положению», а она тем меньше, чем
меньше угол наклонной плоскости или вообще линии перемещения тела по отношению
к горизонту.
Иордан Неморарий понял, что известный в древности
закон равновесия на рычаге и неизвестный закон равновесия на наклонной
плоскости являются частными случаями какого-то общего закона. Еще во времена
Аристотеля считали, что большая тяжесть груза на длинном плече объясняется тем,
что при вращении рычага точка приложения веса описывает большую дугу, чем на
коротком плече. Так как при равновесии двух тел, находящихся на обоих плечах
рычага, их веса должны быть обратно пропорциональны длинам плеч рычага, то
«тяжесть по положению» можно считать пропорциональной произведению веса на
плечо (радиус описываемого круга) или на величину соответствующего изменения
высоты груза. При движении по наклонной плоскости тяжесть по положению зависит
от величины наклона.
Основные положения Иордана формулировались так: груз
тяжелее, если в заданном положении линия его спуска менее наклонна. Более
наклонной линией перемещения является такая, у которой для заданного положения
перемещение по высоте меньше.
Несомненно принадлежащими Иордану являются два сочинения:
«Elementa Iordani de ponderibus» (более короткая ранняя работа) и «Liber de
ratione ponderis» (более поздняя, напечатанная в 1565 г.). Сравнивая изложение
в двух этих произведениях, можно составить представление о ходе мыслей Иордана.
Известно, что два одинаковых груза на концах
равноплечего прямолинейного рычага находятся в равновесии, которое, кроме того,
является безразличным (рис. 22). В «Элементах» Иордан утверждал, что это
равновесие, кроме того, является устойчивым. Доказывал он это так.
Если плечи рычага расположены по горизонтали, то
имеется равновесие. Выведем рычаг из положения равновесия, повернув его в
вертикальной плоскости на некоторый угол. Оба груза, и верхний и нижний,
стремятся двигаться вниз. Можно считать, что они опускаются по наклонным
плоскостям, которые получатся, если соединить хордами начальное и близкое к
нему конечное положения обоих грузов, предполагая, что они двигаются вниз,
описывая дуги одинаковой величины. Нетрудно видеть, что у нижнего груза
наклонная плоскость более полога, чем у верхнего, перемещение которого более
близко к вертикальному. Тогда, согласно определению, верхний груз будет иметь
большую тяжесть по положению, следовательно, рычаг вернется в горизонтальное
положение равновесия.
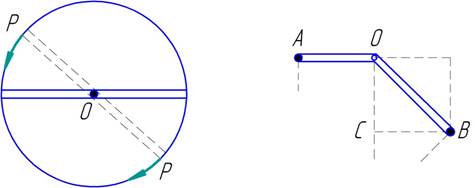
Рис. 22
Рис. 23
В той же книге «Элементов» Иордан рассматривает
ломаный рычаг АОВ (рис. 23), плечо ОА которого расположено горизонтально, а
плечо ОВ лежит в вертикальной
плоскости, направлено вниз и занимает такое положение, что его конец В находится на расстоянии ВС = ОА
от вертикали, проведенной через центр О.
Если в точках А
к В помещены одинаковые грузы, то
система находится в равновесии, когда плечо ОА
направлено по горизонтали. Но так как груз А,
выходя из заданного положения, опускается по вертикали, а груз В — по наклонной плоскости,
перпендикулярной к ОВ, то «тяжесть по
положению» груза А больше, чем у
груза В, и следовательно, равновесие нарушается.
В книге «Liber de ratione ponderis», представляющей дальнейшую стадию развития «Науки о
весах», этих предложений нет. Иордан отбросил их, как ошибочные, и дал новое
определение «тяжести по положению». Первоначально он считал, что она зависит только
от угла наклона перемещения (в случае наклонной плоскости — от того угла,
который она образует с горизонтом); теперь он понял, что при сравнении
перемещений обоих грузов существенное значение имеют вертикальные составляющие
обоих перемещений.
Обычно считают, что «тяжесть по положению» груза Р на наклонной плоскости равна
составляющей веса по наклонной плоскости Psinα,
где α —угол плоскости с горизонтом. Это равносильно тому, что из
Архимедова условия — равновесие грузов на рычаге Ра = Qb — делается вывод,
что Архимед полагал ϱοπή т. е. момент, равным произведению
силы на плечо. Уже сам факт наличия рычагов в рассуждениях Иордана показывает,
что его определение «тяжести по положению» имело более общий характер и
применимо не только для наклонной плоскости.
Действительно, в книге «Liber de ratione ponderis»
содержатся следующие предложения.
Предложение 6. Если плечи рычага пропорциональны весам
подвешенных грузов так, что более тяжелый груз подвешен к более короткому
плечу, то оба эти груза имеют одинаковые тяжести по положению.
Предложение 8. Если плечи рычага не равны и образуют
угол в центре движения и если концы этих плеч находятся на одинаковых
расстояниях от вертикали, проходящей через точку опоры, то в этом положении
подвешенные равные грузы имеют одинаковые тяжести по положению.
Уже во времена Герона было известно, что закон рычага
можно обобщать и для случая, когда плечи не лежат на одной прямой; они могут
быть даже криволинейными, лишь бы находились в одной плоскости с центром
рычага. Для Иордана существенно главным образом отношение величины вертикальных
перемещений.
В предложении 10 Иордан переходит к закону равновесия
на наклонной плоскости.
Предложение 10. Если два груза опускаются по путям с
различными наклонностями, которые пропорциональны весам грузов, взятым в
обратном порядке, то эти грузы имеют одинаковые тяжести по положению.
Пусть прямая ABC
(рис. 24) параллельна горизонту; восставим к ней перпендикуляр BD. Пусть из D спускаются прямые DA и DC и пусть DC имеет большую наклонность. Отношение наклонностей определяется
отношением не углов, а длин наклонных линий, измеряемых до горизонтальной
прямой, отсекающей от обеих начальных прямых одинаковые отрезки на вертикали DB.
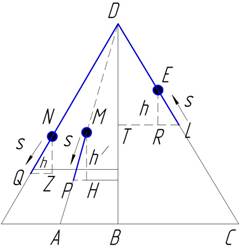
Рис. 24
Пусть на DC
лежит груз е, а на DA — груз b. Пусть е относится к b, как DC к DA.
Предполагается, что оба груза соединены веревкой,
проходящей через вершину D. Сначала
рассмотрим случай, когда оба груза равны и соответственно обе плоскости имеют
одинаковый наклон. Очевидно, что оба груза находятся в равновесии. Если один из
них опустим по плоскости на длину s,
то второй по соответствующей плоскости подымется на такую же длину s; произведения величины груза на
перемещение одинаковы.
Предположим теперь, что одна из плоскостей стоит более
круто. Теперь, хотя и веса и перемещения s
для обоих грузов остаются одинаковыми, но груз, находящийся на более крутой
плоскости, перетянет, потому что у него МН
— вертикальное перемещение (проекция s на вертикаль больше, чем NZ = ER
= h); для равновесия нужно
соответственно увеличить груз, находящийся на другой плоскости, так, чтобы
произведения грузов на вертикальное перемещение были одинаковы для обоих
грузов.
Если BD —
высота точки D над горизонтом, то
тяжести по положению обоих грузов равны
![]()
![]()
Сравнивая
их, получаем условия равновесия в виде
![]()
Эти условия подобны условиям равновесия грузов на
рычаге, если вместо длины наклонных плоскостей поставить величины
соответствующих плеч и обратную пропорциональность заменить прямой.
Теперь можно установить, какое отношение имеют
изложенные предложения к определению давлений тяжелых тел на опоры.
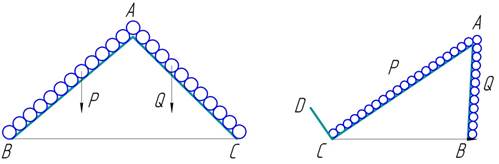
Рис. 25
Рис. 26
Иордан утверждает, что не обязательно, чтобы
уравновешивающиеся на наклонных плоскостях грузы представляли материальные тела
(рис. 25); эти грузы можно равномерно распределить по обеим сторонам
треугольника, изображающего соответствующие плоскости. Тогда получатся две
однородные линии, или цепочки, веса Р
и Q которых относятся как длины АВ и АС
соответствующих плоскостей; если это условие соблюдено, то веса Р и Q
находятся в равновесии.
Пусть теперь требуется определить давление груза Р, имеющего произвольную форму, лежащего
на наклонной плоскости АС и
Удерживаемого в покое загородкой CD,
перпендикулярной к АС (рис. 26). Для
этого достаточно распределить груз Р
по плоскости АС и затем продолжить
полученную ленту по вертикали АВ.
Если вес полученной части равен Q, то
давление груза Р на CD равно давлению ленты АВ на горизонтальную площадь, помещению
в точке В, т. е. весу Q.
Возьмем лежащую на наклонных плоскостях цепь ВАС и соединим ее концы В и С
свободно висящей однородной цепочкой из такого же материала, что и ВАС; тогда получим чертеж, при помощи
которого нидерландский механик Стевин
доказывал условие равновесия тяжелых тел на наклонной плоскости. Его
доказательство основано на предположении о невозможности вечного движения,
которое получилось бы, если лежащая на ABC
цепочка не находилась в равновесии. Но, если она находится в равновесии, то
можно откинуть свободно висящую часть, которую следует рассматривать как
симметричную однородную цепь, подвешенную на концах В и С и, очевидно,
находящуюся в равновесии.
Таким образом, работа Иордана Неморария не осталась
бесплодной; ее непосредственным продолжателем был Симон Стевин (1548—1626). Он родился в Брюгге (в теперешней
Бельгии); первоначально он работал бухгалтером; следом таких занятий (кроме
учебника бухгалтерии) осталась его знаменитая книга «Disme» («Десятка»). В ней
он предложил десятичную систему мер и в соответствии с этим десятичные дроби,
которые после него вошли во всеобщее употребление. Время его жизни совпадало с
эпохой борьбы Нидерланд против испанского владычества; из Брюгге ему пришлось
бежать; после нескольких лет скитаний он попал в Голландию, где прошла большая часть его жизни
на службе у принца Морица Нассаусского — младшего брата Вильгельма Оранского,
вождя нидерландского народа в борьбе за освобождение. Мориц осуществлял
техническую подготовку военных действий, обучение регулярной армии (между
прочим, это была первая регулярная армия в Западной Европе), постройку судов и
военных укреплений, в этой области ему много помогал Стевин.
Стевина обычно считают родоначальником аксиомы
параллелограмма сил в форме силового треугольника, который так и называется
треугольником Стевина.
Так как Стевин был продолжателем Иордана, установим,
знал ли он о его работах., Нужно отметить, что работа «De Ratione Ponderis»
Иордана Неморария была напечатана в 1565 г., поэтому Стевин мог ее знать.
Заглавие основного произведения Стевина «Beghinselen der Weegkonst» («Начала науки о весах») представляет собой
перевод «Scientia de Ponderibus» Неморария. Стевин, как большой патриот голландского
языка, переводил на него все научные термины: так, математика называлась у него
Wiskunde, геометрия— Meetkunde (наука об измерении); Weegkonst — буквально
«Искусство взвешивания» — он считал особой наукой, стоящей наряду с геометрией.
Он говорил, что геометрия изучает форму и величину фигур и тел, не обращая
внимания на их вес, а наука о весах имеет дело с весами тел и не обращает
внимания на их величину и форму. Именно Стевин ввел в механику термин
«равновесие» вместо греческой «равномоментности».
«Начала науки о весах», которое теперь можно назвать
статикой, состоит из двух книг. Вторая из них посвящена определению центров
тяжести и стоит в одном ряду с работами его современников Галилея, Коммандина,
Гульдена и других последователей Архимеда. Первая книга состоит из двух частей:
в одной из них описаны прямые (вертикальные) веса и рассмотрено равновесие параллельных
сил на рычаге; в другой части рассмотрены косые веса, т. е. наклонные силы. Это
вполне соответствует изложению Иордана, у которого рычаги и наклонные плоскости
рассматриваются совместно. Нужно отметить, что в этой книге речь идет только о
равновесии двух сил и никакого силового треугольника нет; но все же Стевин
устанавливает, что линии действия трех уравновешивающихся сил должны
пересекаться в одной точке.
Во втором издании книги «Beghinselen der Weegkonst»
Стевин сделал несколько добавлений. Из них особенно интересны два:
«Спартостатика», в котором рассматриваются условия равновесия груза,
подвешенного на веревках, и «Трохлеостатика», где определяются величины сил,
действующих в полиспастах.
«Спартостатика» представляет собой собрание замечаний
к первой книге «Beghinselen», сделанных без формулировок и доказательств. В
одном из них рассматривается груз Р, прикрепленный узлом в точке С к двум веревкам CD и СЕ (рис. 27). Стевин
проводит вертикаль CF и из
произвольной точки Н левой веревки
прямую HI, параллельную направлению
второй веревки СЕ. Он утверждает
следующее: как СI относится к IH, так и вес Р относится к весу, приходящемуся на веревку СЕ. Как СH относится к IH, так и вес, приходящийся на веревку CD, относится к весу, приходящемуся на
веревку СЕ.
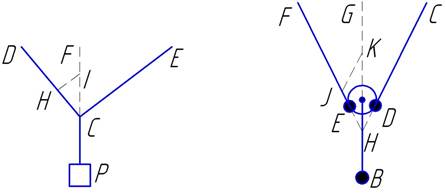
Рис. 27
Рис. 28
Задача решена совершенно правильно. Треугольник CIH можно рассматривать как современный
треугольник Стевина с той лишь разницей, что стороны его представляют не силы,
а только пропорциональные им длины. Никаких формулировок и доказательств Стевин
не дает: имеется лишь чертеж с объяснением.
Можно было бы признать за Стевином право открытия
силового треугольника, если бы не было второго добавления — «Трохлеостатика». В
ней Стевин рассматривает силы, действующие в полиспастах. Если все веревки
вертикальны, то, разделив величину поднимаемого груза на число веревок,
получаем силу, которую надо приложить к свободному концу веревки полиспаста,
чтобы получить равновесие. Этот случай был рассмотрен в «Механике» Герона и
ничего нового не представляет. Но Стевину надо было получить совершенно новый
результат, а именно — рассмотреть случай полиспаста с двумя непараллельными
веревками.
На рис. 28 груз В
прикреплен к блоку ED, лежащему
на веревке FEDC, конец С которой
закреплен, a F удерживается рукой.
Линия (веревка), на которой висит груз В, продолжена вверх к точке G (линия BG), a FE — вниз до
пересечения ее линией BG в точке Н. После этого через какую-либо точку I веревки HF проводится линия IK
параллельно DC до пересечения ее
линией BG в точке К.
Как линия IK
относится к линии КН, так и
приходящийся в точке F вес относится
к заданному весу В. Так же как линия HI относится к линии IK, так и вес,
приходящийся в точке F, относится к
весу длины DC, Никакой формулировки и
доказательств нет; это похоже на записи Леонардо да Винчи. Таким образом,
приведенный чертеж доказательной силы иметь не может, тогда как в сочинении
«Beghinselen» все это имеется полностью.
Во втором добавлении «Трохлеостатика» рассмотрены
силы, действующие в полиспастах. Если веревки параллельны, то, разделив
поднимаемый груз на их число, получаем величину силы, которую надо приложить к
свободному концу веревки, соответственно тому, как в «Механике» Герона.
Интересен случай, когда веревки не параллельны. На рис. 28 груз В прикреплен к блоку ED, лежащему на веревке FEDC, конец С которой закреплен, a F
удерживается рукой.
Линию (веревку), на которой висит груз В, продолжаем вверх к G, a FE
— вперед до пересечения ее линией BG
в точке Н.
После этого через какую-либо точку I веревки HF проводим линию IK,
параллельную DC, до пересечения ее
линией BG в точке K.
Следовательно, что как I относится к КН, так и
приходящийся на руку в точке F вес
относится к заданному весу; как HI
относится к IK, так и вес,
приходящийся на руку в точке F,
относится к весу, действующему на С;
каждый из них составляет половину веса, который к заданному весу находится в
отношении НК и HI (на основании вышеприведенного замечания из «Спартостатики»).
Если G
обозначает вес В, то действующая на
точку F сила вычисляется по формуле
![]()
однако
правильный результат был бы
![]()
По-видимому, ход мыслей Стевина был таков: если бы
веревки EF и DC были параллельны, то на каждую из них действовала бы половина
веса G; поскольку же они не
параллельны, то соответствующий вес должен быть больше половины G. Поэтому вес G должен быть увеличен в отношении соответствующих сторон КН и IH
треугольника Стевина.
Основная причина неудачи Стевина, конечно, заключается
в том, что векторный характер силы в его время был еще неизвестен.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов