Главная

Лекция 2. Поступательное и вращательное движение твердого тела.

В данной лекции рассматриваются следующие вопросы:

1. Степени свободы твердого тела.

2. Поступательное и вращательное движения твердого тела.

3. Поступательное движение.

4. Движение тела по окружности.

5. Вращательное движение твердого тела вокруг оси.

6. Угловая скорость и угловое ускорение.

7. Равномерное и равнопеременное вращения.

8. Скорости и ускорения точек вращающегося тела.

9. Вращение тела вокруг неподвижной точки.

Изучение данных вопросов необходимо в дальнейшем для динамики движения материальной точки, динамики относительного движения точки, динамики вращательного движения точки, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».

Степени свободы твердого тела

Числом степеней свободы твердого тела называется число независимых параметров, которые однозначно определяют положение тела в пространстве относительно рассматриваемой системы отсчета. Движение твердого тела во многом зависит от числа его степеней свободы.

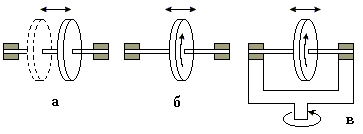
Рис.1

Рассмотрим пример. Если диск, не вращаясь, может скользить вдоль неподвижной в данной системе отсчета оси (рис.1,а), то в данной системе отсчета он, очевидно, обладает только одной степенью свободы - положение диска однозначно определяется, скажем, координатой x его центра, отсчитываемой вдоль оси. Но если диск, кроме того, может еще и вращаться (рис.1,б), то он приобретает еще одну степень свободы - к координате x добавляется угол поворота φ диска вокруг оси. Если ось с диском зажата в рамке, которая может поворачиваться вокруг вертикальной оси (рис.1,в), то число степеней свободы становится равным трем – к x и φ добавляется угол поворота рамки ϕ.

Свободная материальная точка в пространстве имеет три степени свободы: например декартовы координаты x, y и z. Координаты точки могут определяться также в цилиндрической (r, 𝜑, z) и сферической (r, 𝜑, 𝜙) системах отсчета, но число параметров, однозначно определяющих положение точки в пространстве всегда три.

Материальная точка на плоскости имеет две степени свободы. Если в плоскости выбрать систему координат xОy, то координаты x и y определяют положение точки на плоскости, а координата z тождественно равна нулю.

Свободная материальная точка на поверхности любого вида имеет две степени свободы. Например: положение точки на поверхности Земли определяется двумя параметрами: широтой и долготой.

Материальная точка на кривой любого вида имеет одну степень свободы. Параметром, определяющим положение точки на кривой, может быть, например, расстояние вдоль кривой от начала отсчета.

Рассмотрим две материальные точки в пространстве, соединенные жестким стержнем длины l (рис.2). Положение каждой точки определяется тремя параметрами, но на них наложена связь.

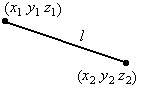
Рис.2

Уравнение l²=(x₂-x₁)²+(y₂-y₁)²+(z₂-z₁)² является уравнением связи. Из этого уравнения любая одна координата может быть выражена через остальные пять координат (пять независимых параметров). Поэтому эти две точки имеют (2∙3-1=5) пять степеней свободы.

Рассмотрим три материальные точки в пространстве, не лежащие на одной прямой, соединенные тремя жесткими стержнями. Число степеней свободы этих точек равно (3∙3-3=6) шести.

Свободное твёрдое тело в общем случае имеет 6 степеней свободы. Действительно, положение тела в пространстве относительно какой-либо системы отсчета, определяется заданием трех его точек, не лежащие на одной прямой, и расстояния между точками в твердом теле остаются неизменными при любых его движениях. Согласно выше сказанному, число степеней свободы должно быть равно шести.

Поступательное и вращательное движения твердого тела.

Поступательное движение

В кинематике, как и в статистике, будем рассматривать все твердые тела как абсолютно твердые.

Абсолютно твердым телом называется материальное тело, геометрическая форма которого и размеры не изменяются ни при каких механических воздействиях со стороны других тел, а расстояние между любыми двумя его точками остается постоянным.

Кинематика твердого тела, также как и динамика твердого тела, является одним из наиболее трудных разделов курса теоретической механики.

Задачи кинематики твердого тела распадаются на две части:

1) задание движения и определение кинематических характеристик движения тела в целом;

2) определение кинематических характеристик движения отдельных точек тела.

Существует пять видов движения твердого тела:

1) поступательное движение;

2) вращение вокруг неподвижной оси;

3) плоское движение;

4) вращение вокруг неподвижной точки;

5) свободное движение.

Первые два называются простейшими движениями твердого тела.

Начнем с рассмотрения поступательного движения твердого тела.

Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему начальному направлению.

Поступательное движение не следует смешивать с прямолинейным. При поступательном движении тела траектории его точек могут быть любыми кривыми линиями. Приведем примеры.

1. Кузов автомобиля на прямом горизонтальном участке дороги движется поступательно. При этом траектории его точек будут прямыми линиями.

2. Спарник АВ (рис.3) при вращении кривошипов O₁A и O₂B также движется поступательно (любая проведенная в нем прямая остается параллельной ее начальному направлению). Точки спарника движутся при этом по окружностям.

Рис.3

Поступательно движутся педали велосипеда относительно его рамы во время движения, поршни в цилиндрах двигателя внутреннего сгорания относительно цилиндров, кабины колеса обозрения в парках (рис.4) относительно Земли.

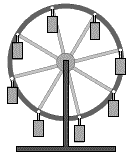
Рис.4

Свойства поступательного движения определяются следующей теоремой: при поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.

Для доказательства рассмотрим твердое тело, совершающее поступательное движение относительно системы отсчета Oxyz. Возьмем в теле две произвольные точки А и В, положения которых в момент времени t определяются радиусами-векторами и (рис.5).

Рис.5

Проведем вектор , соединяющий эти точки.

Тогда

При этом длина АВ постоянна, как расстояние между точками твердого тела, а направление АВ остается неизменным, так как тело движется поступательно. Таким образом, вектор АВ во все время движения тела остается постоянным (AB=const). Вследствие этого, траектория точки В получается из траектории точки А параллельным смещением всех ее точек на постоянный вектор . Следовательно, траектории точек А и В будут действительно одинаковыми (при наложении совпадающими) кривыми.

Для нахождения скоростей точек А и В продифференцируем обе части равенства по времени. Получим

Но производная от постоянного вектора АВ равна нулю. Производные же от векторов и по времени дают скорости точек А и В. В результате находим, что

т.е. что скорости точек А и В тела в любой момент времени одинаковы и по модулю, и по направлению. Беря от обеих частей полученного равенства производные по времени:

Следовательно, ускорения точек А и В тела в любой момент времени тоже одинаковы по модулю и направлению.

Так как точки А и В были выбраны произвольно, то из найденных результатов следует, что у всех точек тела их траектории, а также скорости и ускорения в любой момент времени будут одинаковы. Таким образом, теорема доказана.

Из теоремы следует, что поступательное движение твердого тела определяется движением какой-нибудь одной из его точки. Следовательно, изучение поступательного движения тела сводится к задаче кинематике точки, нами уже рассмотренной.

При поступательном движении общую для всех точек тела скорость называют скоростью поступательного движения тела, а ускорение - ускорением поступательного движения тела. Векторы и можно изображать приложенными в любой точке тела.

Заметим, что понятие о скорости и ускорении тела имеют смысл только при поступательном движении. Во всех остальных случаях точки тела, как мы увидим, движутся с разными скоростями и ускорениями, и термины <<скорость тела>> или <<ускорение тела>> для этих движений теряют смысл.

Движение тела по окружности с постоянной по модулю скоростью

Движение тела по окружности с постоянной по модулю скоростью - это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.

Положение тела на окружности определяется радиусом-вектором , проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 6).

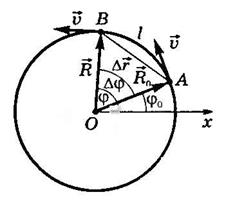
Рис.6

За время ∆t тело, двигаясь из точки А в точку В, совершает перемещение , равное хорде АВ, и проходит путь, равный длине дуги l.

Радиус-вектор поворачивается на угол ∆φ. Угол выражают в радианах.

Скорость движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью. Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени ∆t, за который эта дуга пройдена:

Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью:

В СИ единицей угловой скорости является радиан в секунду .

При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω=const; v=const.

Положение тела можно определить, если известен модуль радиуса- вектора и угол φ, который он составляет с осью Ох (угловая координата). Если в начальный момент времени t₀=0 угловая координата равна φ₀, а в момент времени t она равна φ, то угол поворота ∆φ радиуса-вектора за время ∆t=t-t₀ равен ∆φ=φ-φ₀. Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности:

φ=φ₀+ωt

Оно позволяет определить положение тела в любой момент времени t.

Учитывая, что , получаем:

— формула связи между линейнойи угловой скоростью.

Промежуток времени Т, в течение которого тело совершает один полный оборот, называется периодом вращения:

где N – число оборотов, совершенных телом за время Δt.

За время ∆t=Т тело проходит путь l=2πR. Следовательно,

Величина ϑ, обратная периоду, показывающая, сколько оборотов совершает тело за единицу времени, называется частотой вращения:

Следовательно,

.

Ускорение при движении тела по окружности с постоянной по модулю скоростью (центростремительное ускорение)

При равномерном вращении по окружности модуль скорости движения тела не изменяется, но направление скорости изменяется непрерывно. Следовательно, данное движение - движение с ускорением. Оно характеризует быстроту изменения скорости по направлению.

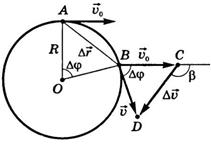
Рис.7

По определению среднего ускорения . Треугольники ОАВ и ВСD — равнобедренные (рис. 7). Углы при вершинах — одинаковые (как углы с соответственно перпендикулярными сторонами). Отсюда следует, что ∆ОАВ подобен ΔВСD.

Из подобия

Тогда

Мгновенное ускорение

β — угол между и —внешний по отношению к ΔВСD:

При ∆t→0 угол ∆φ→0 и, следовательно, β→90°. Перпендикуляром к касательной к окружности является радиус. Следовательно, направлено по радиусу к центру и поэтому называется центростремительным ускорением:

Модуль , направление непрерывно изменяется (рис. 8). Поэтому данное движение не является равноускоренным.

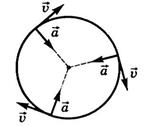
Рис.8

Вращательное движение твердого тела вокруг оси. Угловая скорость и угловое ускорение

Для кинематического описания вращательного движения абсолютно твердого тела вокруг неподвижной оси используются те же величины, что и для описания движения материальной точки по окружности.

Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными (рис.9).

Промежуток времени, в течение которого тело совершает один полный оборот вокруг оси, — период вращения. Величина, обратная периоду, — частота вращения.

Проходящая через неподвижные точки А и В прямая АВ называется осью вращения.

Так как расстояния между точками твердого тела должны оставаться неизменными, то очевидно, что при вращательном движении все точки, принадлежащие оси вращения, будут неподвижны, а все остальные точки тела будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси.

Для определения положения вращающегося тела проведем через ось вращения, вдоль которой направим ось Az, полуплоскость - неподвижную и полуплоскость, врезанную в само тело и вращающуюся вместе с ним (рис. 9).

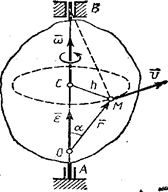
Рис.9

Тогда положение тела в любой момент времени однозначно определится взятым с соответствующим знаком углом φ между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол φ положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az), и отрицательным, если по ходу часовой стрелки. Измерять угол φ будем всегда в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла φ от времени t, т.е.

φ=f(t).

Уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси.

При вращательном движении абсолютно твердого тела вокруг неподвижной оси углы поворота радиуса-вектора различных точек тела одинаковы.

Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость ω и угловое ускорение ε.

Если за промежуток времени ∆t=t₁-t тело совершает поворот на угол ∆φ=φ₁-φ, то численно средней угловой скоростью тела за этот промежуток времени будет . В пределе при ∆t→0 найдем, что

или ω=.

Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени. Знак ω определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки, ω>0, а когда по ходу часовой стрелки, то ω<0.

Размерность угловой скорости 1/Т (т.е. 1/время); в качестве единицы измерения обычно применяют рад/с или, что тоже, 1/с (с^-1), так как радиан - величина безразмерная.

Угловую скорость тела можно изобразить в виде вектора , модуль которого равен || и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.10). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.

Рис.10

Угол поворота и угловая скорость характеризуют движение всего абсолютно твердого тела в целом. Линейная скорость какой-либо точки абсолютно твердого тела пропорциональна расстоянию точки от оси вращения:

При равномерном вращении абсолютно твердого тела углы поворота тела за любые равные промежутки времени одинаковы, тангенциальные ускорения у различных точек тела отсутствуют, а нормальное ускорение точки тела зависит от ее расстояния до оси вращения:

Вектор направлен по радиусу траектории точки к оси вращения.

Угловое ускорение характеризует изменение с течением времени угловой скорости тела. Если за промежуток времени ∆t=t₁-t угловая скорость тела изменяется на величину ∆ω=ω₁-ω, то числовое значение среднего углового ускорения тела за этот промежуток времени будет . В пределе при ∆t→0 найдем,

Таким образом, числовое значение углового ускорения, тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела по времени.

Размерность углового ускорения 1/T² (1/время²); в качестве единицы измерения обычно применяется рад/с² или, что то же, 1/с² (с-²).

Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает, - замедленным. Легко видеть, что вращение будет ускоренным, когда величины ω и ε имеют одинаковые знаки, и замедленным, - когда разные.

Угловое ускорение тела (по аналогии с угловой скоростью) можно также изобразить в виде вектора ε, направленного вдоль оси вращения. При этом

Направление ε совпадает с направлением ω, когда тело вращается ускоренно и (рис.10,а), противоположно ω при замедленном вращении (рис.10,б).

Равномерное и равнопеременное вращения

Если угловая скорость тела остается во все время движения постоянной (ω=const), то вращение тела называется равномерным. Найдем закон равномерного вращения. Из формулы имеем dφ=ωdt.

Отсюда, считая, что в начальный момент времени t=0 угол φ=φ₀, и беря интегралы слева от φ₀ до φ, а справа от 0 до t, получим окончательно

φ=φ₀+ωt.

Из равенства следует, что при равномерном вращении, когда φ₀=0

φ=ωt и ω=φ/t.

В технике скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину через n об/мин. Найдем зависимость между n об/мин и ω 1/с. При одном обороте тело повернется на угол 2π, а при n оборотах на 2πn; этот поворот делается за время t = 1 мин = 60 сек. Из равенства следует тогда, что

ω=π∙n/30≈0,1n.

Если угловое ускорение тела во все время движения остается постоянным (ε=const), то вращение называется равнопеременным. Найдем закон равнопеременного вращения, считая, что в начальный момент времени t=0 угол φ=φ₀, а угловая скорость ω=ω₀ (ω₀ - начальная угловая скорость).

Из формулы имеем dω=ε∙dt. Интегрируя левую часть в пределах от ω₀ до ω, а правую - в пределах от 0 до t, найдем ω=ω₀+εt,

dφ/dt=ω₀+εt или dφ=ω₀dt+εtdt.

Вторично интегрируя, найдем отсюда закон равнопеременного вращения

Если величины ω и ε имеют одинаковые знаки, то вращение будет равноускоренным, а если разные - равнозамедленным.

Скорости и ускорения точек вращающегося тела.

Установив характеристики движения всего тела в целом, перейдем к изучению движения отдельных его точек.

1. Скорости точек тела. Рассмотрим какую-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения (см. рис.9). При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время dt происходит элементарный поворот тела на угол dφ, то точка М при этом совершает вдоль своей траектории элементарное перемещение ds=hdφ. Тогда числовое значение скорости точки будет равно отношению ds к dt, т.е

Скорость в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.

Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения.

Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М.

Так как для всех точек тела имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.

Рис.11 Рис. 12

2. Ускорения точек тела. Для нахождения ускорения точки М воспользуемся формулами

В нашем случае ρ=h. Подставляя значение v в выражения a_τ и a_n, получим:

или окончательно:

Касательная составляющая ускорения a_τ направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при, замедленном); нормальная составляющая a_n всегда направлена по радиусу МС к оси вращения (рис.12). Полное ускорение точки М будет

Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом μ, который вычисляется по формуле

Подставляя сюда значения a_τ и a_n, получаем

Так как ω и ε имеют в данный момент времени для всех точек тела одно и то же значение, то ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол μ с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис.14.

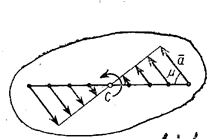
Рис.13 Рис.14

3. Векторы скорости и ускорения точек тела. Чтобы найти выражения непосредственно для векторов v и a, проведем из произвольной точки О оси АВ радиус-вектор точки М (рис. 13). Тогда h=r∙sinα и по формуле

Таким образом, модуль векторного произведения равен модулю скорости точки М. Направления векторов и v тоже совпадают (оба они перпендикулярны плоскости ОМВ) и размерности их одинаковы. Следовательно, - формула Эйлера, т.е. вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки.

Пример 1. Маятник OM качается в вертикальной плоскости так, что φ=0,5sin2t. Длина OM=l=1м. (рис. 15).

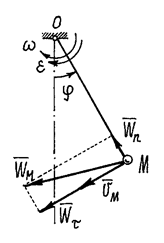
Рис.15

Решение. Маятник вращается вокруг горизонтальной оси О, перпендикулярной вертикальной плоскости. Угловая скорость угловое ускорение

Например, при t=1 с, φ=0,5sin2=0,45 рад≅26°; ω=cos2=-0,42 c^-1 (вращение по часовой стрелке); ε=-2sin2=-1,82 c^-2 (угловое ускорение направлено также по часовой стрелке). Вращение в этом положении ускоренное.

Скорость точки M: v_M=lω=1∙0,42=0,42 м∙с^-1 (определяется модуль скорости). Направлен вектор скорости соответственно направлению угловой скорости – в сторону вращения.

.

Нормальное ускорение a_n=lω²=1∙0,42²=0,176 м∙с^-2, касательное ускорение a_τ=lε=1∙1,82=1,82 м∙с^-2. (Определён опять модуль вектора ускорения. Направлен вектор вниз, как указывает угловое ускорение).

Величина полного ускорения точки

Вращение тела вокруг неподвижной точки

Название такого вида движения довольно точно его определяет. Часто это движение называют сферическим движением потому, что все точки тела движутся по сферическим поверхностям.

Наглядным примером такого движения является волчок, закономерности движения которого лежат в основе гироскопических приборов.

1) Углы Эйлера. Уравнения вращения тела с одной неподвижной точкой.

Рис. 9.5.

Рис. 9.5.

Положение тела определяется тремя углами. Используются различные системы углов. Например, корабельные углы, самолётные углы и др. Но самыми распространёнными являются углы Эйлера: Ψ (пси), 𝜃(тета), φ (фи).

Положение тела определяется следующим образом. Назначаются две системы декартовых осей. Первая система – неподвижные оси x,y,z. Начало которых берётся в неподвижной точке O тела (рис. 16). Вторая система, оси x₁, y₁, z₁, связывается с телом. Поэтому положение тела будет определяться как положение этих осей относительно неподвижных.

Рис.16

Рис. 9.4.

Рис. 9.5.

Когда углы Эйлера равны нулю, подвижные оси совпадают с неподвижными. Чтобы определить положение тела, соответствующее заданным углам Эйлера, производим следующие действия. Сначала подвижные оси, а значит и тело, поворачиваем на угол Ψ вокруг оси z. При этом оси x₁ и y₁ отойдут от осей x и y в горизонтальной плоскости и ось x₁ займёт положение OK (рис.16). Затем тело вращаем вокруг нового положения оси x₁ (прямой OK) на угол θ. Ось z₁ отойдёт от оси z на этот угол θ, а ось y₁ приподнимется над горизонтальной плоскостью. Наконец, тело (и подвижные оси) вращаем вокруг нового положения оси z₁ на угол φ. Ось x₁ отойдёт от положения OK в наклонной плоскости, перпендикулярной оси z₁. Это положение тела и будет соответствовать углам Эйлера (на рисунке само тело не показано).

Линия пересечения неподвижной плоскости xOy и подвижной x₁Oy₁, прямая OK, называется линией узлов. Угол Ψ называется углом прецессии, угол θ – углом нутации, угол φ – углом собственного вращения. Эти названия углов пришли из теории гироскопов.

При движении тела углы Эйлера изменяются по определённым законам Ψ=Ψ(t); θ=θ(t); φ=φ(t) которые называются уравнениями вращения.

На примере вращающегося волчка можно лучше разобраться в этих углах Эйлера (рис.17). Ось волчка z₁ описывает конус вокруг неподвижной оси z. Это вращение определяется углом Ψ (говорят: волчок совершает прецессию). Отклонение оси волчка от вертикали – угол нутации θ.

А вращение волчка вокруг своей оси z₁, определяемое углом φ – собственное вращение.

Рис.17

2) Теорема Даламбера – Эйлера. Мгновенная ось вращения.

Проведём в теле сферическую поверхность произвольного радиуса с центром в неподвижной точке O (рис.18).

Рис.18

Покажем у тела какие-нибудь две точки A и B, расположенные на этой сфере. Соединим их по сфере дугой наибольшего радиуса (кратчайшее расстояние между точками). Переместим тело в новое положение. Точки, а значит и дуга, займут положение A₁ и B₁. Соединим точки A и A₁, B и B₁ дугами большого радиуса AA₁ и BB₁. Посередине этих дуг проведём им перпендикулярные дуги и найдём их точку пересечения P₁. Соединим эту точку P₁ с точками A, B, A₁, B₁. Получим два сферических треугольника ∆ABP₁ и ∆A₁B₁P₁, расположенных на этой сфере. Эти два треугольника равны, как треугольники с равными сторонами (AB=A₁B₁, а AP₁=A₁P₁ и BP₁=B₁P₁ – как дуги равноудалённые от перпендикуляров). Так как эти два треугольника расположены на одной сфере и имеют общую вершину P₁, то их можно совместить поворотом сферы, а значит и тела, вокруг прямой OP₁.

Поэтому можно сделать вывод, что тело с одной неподвижной точкой можно переместить из одного положения в другое поворотом вокруг некоторой оси, проходящей через неподвижную точку O. Это утверждение – есть теорема Даламбера-Эйлера.

Рис. 9.7.

Конечно, такое перемещение не является истинным движением тела. На самом деле тело переходило из первого положения в другое каким-то другим, наверное более сложным путём. Но, если время ∆t такого перехода мало, то это перемещение будет близко к действительному. А при ∆t→0 можно предположить, что для данного момента времени тело поворачивается вокруг некоторой оси Р, проходящей через неподвижную точку O, вращаясь вокруг неё с угловой скоростью . Конечно, для каждого другого момента времени эта ось расположена иначе. Поэтому ось P называют мгновенной осью вращения, а угловую скорость – мгновенной угловой скоростью, вектор которой направлен по оси.

Рис. 9.8.

3) Скорость точек тела.

По теореме Даламбера-Эйлера за малое время ∆t движение тела можно представить как вращение вокруг неподвижной оси OP₁ с некоторой угловой скоростью (рис.19).

Рис.19

Тогда скорость точки M: В пределе, при ∆t→0, угловая скорость будет приближаться к мгновенной угловой скорости , направленной по мгновенной оси вращения P, а скорость точки - к истинному значению:

Но таким же образом находится скорость точки при вращении тела вокруг оси, по которой направлен вектор , в нашем случае – по мгновенной оси вращения P. Поэтому скорость точки можно определить как скорость её при вращении тела вокруг мгновенной оси P. Величина скорости v=h∙ω (рис.19).

Рис. 9.9.

Определение скоростей точек тела значительно упрощается, если известна мгновенная ось вращения P. Иногда её можно найти, если удастся обнаружить у тела хотя бы ещё одну точку, кроме O, скорость которой в данный момент равна нулю, и провести ось P из неподвижной точки О через эту точку. Так как мгновенная ось вращения – геометрическое место точек, скорости которых равны нулю в данный момент времени.

Пример 2. Водило OA=a, вращаясь вокруг вертикальной оси z с угловой скоростью ω₀, заставляет диск радиуса R кататься по горизонтальной плоскости (рис.20).

Рис.20

Рис. 9.10.

Если представить диск как основание конуса с вершиной в неподвижной точке O, то движение диска можно назвать вращением вокруг этой неподвижной точки O.

Так как скорость точки касания диска с плоскостью равна нулю, то мгновенная ось вращения P проходит через эту точку. И вектор мгновенной угловой скорости будет направлен по этой оси.

Точка A вместе с водилом OA вращается вокруг оси z. Поэтому её скорость v_A=aω₀ (рис.20). Эта скорость определяет направление вращения диска вокруг оси P и направление вектора . Величина угловой скорости (h – расстояние от A до оси P). Теперь можно найти скорость любой точки диска, рассматривая его движение как вращение вокруг оси P. Так, например, скорость точки B: v_B=2h∙ω. Так как h=R∙cosα и , , то и v_B=2aω₀.

4) Ускорение точек тела.

Сначала определим угловое ускорение тела . При движении тела вектор угловой скорости изменяется и по величине, и по направлению. Точка, расположенная на его конце будет двигаться по некоторой траектории со скоростью (рис.21).

Рис.21

Если рассматривать вектор как радиус-вектор этой точки, то .

Итак. Угловое ускорение тела можно определить как скорость точки, расположенной на конце вектора угловой скорости:

.

Этот результат называется теоремой Резаля.

Теперь обратимся к определению ускорения точек. Ускорение какой-либо точки M тела

есть сумма двух векторов.

Первый вектор . Модуль его a₁=εr∙sinα₁=ε∙h₁, где h₁ – расстояние от точки M до вектора . Направлен он перпендикулярно и . Но таким же способом определяется касательное ускорение. Поэтому первую составляющую ускорения определяют как касательное ускорение, предполагая, что тело вращается вокруг оси, совпадающей с вектором . И обозначается этот вектор ускорения так

.

Второй вектор Модуль его a₂=ωv∙cosα₂, но α₂=90°, т.к. векторы и перпендикулярны друг другу.

Рис.22

Значит a₂=ωv=ωh₂ω=h₂ω², где h₂ – расстояние от точки М до мгновенной оси P, до вектора .

Направлен вектор перпендикулярно и , т.е. так же как вектор нормального ускорения при вращении вокруг оси P, или вектора . Поэтому этот вектор ускорения и обозначают, соответственно, так:

Итак, ускорение точек тела, вращающегося вокруг неподвижной точки, определяется как сумма двух ускорений:

Этот результат называется теоремой Ривальса.

Заметим, что в общем случае векторы и не совпадают и угол между и не равен 90°, векторы не перпендикулярны друг другу, как это было при вращении тела вокруг неподвижной оси.

Пример 3. Продолжим исследование движения диска (пример 2). Модуль угловой скорости Значит вектор вместе с осью P, которая всегда проходит через точку касания диска с плоскостью, вращается вокруг оси z и описывает конус. Точка М на конце вектора движется по окружности радиуса r=ω∙cosα с угловой скоростью ω₀. Поэтому угловое ускорение диска

Откладывается вектор из неподвижной точки О. Направлен он, как скорость , перпендикулярно водилу OA, параллельно оси х (рис. 23).

Рис.23

Найдём ускорение точки В.

Ускорение . Направлен вектор перпендикулярно OB и расположен в плоскости zO₁y.

Ускорение Вектор направлен по BC, перпендикулярно мгновенной оси P. Модуль вектора найдём с помощью проекций на оси x, y, z:

Значит

Пример 4. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.

Дано: ω=20 рад/с , N=10 об.

Найти: ε-?

Решение. При равномерном вращательном движении имеют место следующие два уравнения: φ=φ_о+ω_оt+εt²/2 и ω= ω_о+εt. По условию ω_о=0, тогда эти уравнения примут вид: φ=εt²/2 и ω = εt. Решая их и учитывая, что φ=2πN, получим окончательно ε=ω²/4πN=3,2 рад/с.

Пример 5. Колесо радиусом 10 см вращается с постоянным угловым ускорением 3,14 рад/с² (рис.24). Найти для точек на ободе колеса к концу первой секунды после начала движения: 1) угловую скорость, 2) линейную скорость, 3) тангенциальное ускорение, 4) нормальное ускорение, 5) полное ускорение и 6) угол, составляемый направлением полного ускорения с радиусом колеса.

Дано: R= 0,1 м, ε=3,14 рад/с²

Найти: ω-? v -? a_τ -? a -?

Рис.24

Решение. 1) При равнопеременном вращательном движении угловая скорость ω = ω_о+εt. По условию ω_о=0, тогда ω = εt, т.е. ω растет пропорционально времени. К концу первой секунды ω=3,14 рад/с.

2) Так как v=ωR, то линейная скорость также пропорционально времени. К концу первой секунды v = 3,14 м/с.

3) Тангенциальное ускорение a_τ=𝜀R не зависит от времени t. В нашем случае a_τ=0,314 м/с².

4) Нормальное ускорение a_n=ω²R=ε²t²R, т.е. нормальное ускорение растет пропорционально квадрату времени: при t=1 c a_n=0,986м/с².

5) Полное ускорение растет со временем по закону: При t=1 c a=1,03 м/с².

6) Имеем , где α - угол, составляемый направлением полного ускорения с радиусом колеса. В начальный момент времени, т.е. при t=0, a =a_τ - полное ускорение направлено по касательной. При t=∞ a = a_n (так как a_τ=const и a_n пропорционально времени), т.е. при t=∞ полное ускорение направлено по нормали. К концу первой секунды sinα=a_τ/a_n=0,314/1,03=0,305, т.е. α=17^о46’.

Пример 6. Колесо вращается равноускоренно с угловым ускорением ε= 3 рад/с². Определить, какой угловой скорости достигнет тело после t=3 с своего вращения? Сколько оборотов N оно при этом совершит?

Решение. Если тело вращается равноускоренно, то его движение описывает следующая система уравнений

В начальный момент тело покоилось, значит, ω₀=0. Тогда

Следовательно, ω=εt=3∙3=9 рад/с.

Количество оборотов

Пример 7. Вентилятор вращался с частотой n₀=900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N=75 об. Какое время t прошло с момента выключения до остановки вентилятора? С каким угловым ускорением ε он двигался?

Решение. Равнозамедленное движение вентилятора описывается следующей системой уравнений

Поскольку вентилятор остановился, то его конечная частота n=0. Тогда выразим из второго уравнения и, подставив его в первое уравнение, а также учитывая, что n₀=900 об/мин = 15 об/с, получим

Время движения равно

Пример 8. Точка вращается по окружности радиусом R=20 см с постоянным тангенциальным ускорением a_τ=5 см/с². Через какое время после начала вращения нормальное ускорение точки будет вдвое больше тангенциального?

Решение. Угловая скорость точки при равноускоренном движении может быть найдена из соотношения ω=ω₀+εt. Так как ω₀=0, то ω=εt. Нормальное ускорение a_n=ω²R=(εt)²R. Тангенциальное ускорение a_τ=εR. По условию задачи a_n=2a_τ, тогда (εt)²R=2εR, следовательно, εt²=2 и

Пример 9. Точка движется по окружности радиусом R=2 см. Зависимость пути от времени дается уравнением s(t)=Ct³, где С = 0,1 см/с³. Найти нормальное и тангенциальное ускорения точки в тот момент, когда линейная скорость точки v= 0,3 м/с.

Решение. Зависимость пути от времени позволяет найти зависимости от времени скорости и тангенциального ускорения.

Отсюда,

Тогда тангенциальное ускорение a_τ=6∙Ct=6∙0,1∙10^-2∙10=0,06 м/с².

Нормальное ускорение

Пример 10. Точка движется по окружности радиусом R = 4 м. Начальная скорость точки равна 3 м/с, тангенциальное ускорение a_τ = 1 м/с². Для момента времени t = 2 с определить: а) длину пути, пройденного точкой, б) модуль перемещения; в) линейную и угловую скорости; г) нормальное, полное и угловое ускорения.

Рис.25

Решение. Уравнение зависимости пути, пройденного точкой, от времени имеет вид (м). Это позволяет найти длину пути м. Если учесть, что за один оборот точка проходит путь, равный длине окружности s₁=2πR=8π м, то можно найти угловое перемещение точки из пропорции , φ=2 (рад) = 114,7⁰. Тогда модуль перемещения может быть найден по теореме косинусов как хорда, стягивающая этот угол φ.

Линейная скорость точки v=v₀+a_τt=3+1∙2=5 м/с.

Угловая скорость ω=vR=5∙4=20 рад/с.

Нормальное ускорение

Полное ускорение Модуль полного ускорения

Угловое ускорение

Пример 11. Автомобиль, движущийся со скоростью 36 км/ч, проходит закругленное шоссе с радиусом кривизны 200 м. На повороте шофер тормозит машину, сообщая ей ускорение 0,3 м/с². Найти нормальное и полное ускорения автомобиля на повороте. Найти угол между вектором полного ускорения автомобиля на повороте и вектором его скорости. Каковы угловые скорость и ускорение автомобиля в момент вхождения машины в поворот?

Рис.26

Решение. Зная скорость автомобиля v=36 км/ч =10 м/с, найдем его нормальное ускорение

Полное ускорение автомобиля

Угловое ускорение

Угловая скорость

Поскольку движение автомобиля замедленное, то векторы скорости и тангенциального ускорения направлены в противоположные стороны, поэтому вектор скорости и вектор полного ускорения образуют тупой угол φ. Для нахождения этого угла определим вначале угол α, дополняющий искомый угол до 180⁰.

Пример 12. Найти радиус R вращающегося колеса, если известно, что линейная скорость v₁ точки, лежащей на ободе, в 2,5 раза больше линейной скорости v₂, точки, лежащей на расстоянии r =5 cм ближе к оси колеса.

Дано: v₂=2,5v₁, r=R-5

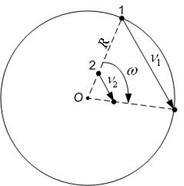
Рис.27

Решение.

1) У точек находящихся на колесе и лежащих на радиусе, будут одинаковы угловые скорости. Используем связь угловой и линейной скоростей:

т.к. ω₁=ω₂, приравниваем правые части уравнений:

Решим уравнение относительно R:

Ответ: Радиус вращающегося колеса равен 8,33 см.

Пример 13. На рис.28 показаны направления вращения гироскопа (волчка) и указано, увеличивается или уменьшается угловая скорость. Укажите номер рисунка, на котором правильно указано направление углового ускорения.

Рис.28

Решение. Псевдовектор угловой скорости связан с направлением вращения правилом буравчика (правого винта). На рис.28.1 и рис.28.3 он направлен вверх, на рис.28.2 и рис.28.4 - вниз.

При возрастании угловой скорости ее приращение, а соответственно и вектор углового ускорения совпадают с вектором угловой скорости (рисунки 1 и 4). При уменьшении угловой скорости ее приращение, а соответственно и вектор углового ускорения противоположны вектору угловой скорости (рис.28.2 и рис.28.3). Следовательно, на всех рисунках направление углового ускорения указано правильно.

Пример 14. Опишите движение вращающегося твердого тела в случаях, когда угловая скорость изменяется согласно графикам 1 и 2, изображенным на рис.29.

Рис.29

Решение. Начнем с того, что вращение бывает в двух направлениях - по часовой стрелке и против. С направлением вращения связан псевдовектор угла поворота и угловой скорости. Пусть положительным будем считать направление вращения по часовой стрелке.

Для движения 1 угловая скорость возрастает, но угловое ускорение ε=dω/dt (производная) уменьшается, оставаясь положительным. Следовательно, это движение является ускоренным по часовой стрелке с уменьшающимся по величине ускорением.

Для движения 2 угловая скорость уменьшается, затем достигает в точке пересечения с осью абсцисс нуля, а далее становится отрицательной и возрастает по модулю. Угловое ускорение (вспомните геометрический смысл производной) отрицательно и уменьшается по модулю. Таким образом, сначала точка двигалась по часовой стрелке замедленно с уменьшающимся по модулю угловым ускорением, остановилась и стала вращаться ускоренно с уменьшающимся по модулю ускорением (оба вектора - и угловая скорость, и угловое ускорение направлены в одну сторону).

Пример 15. Скорость точки, движущейся по кривой, уменьшается по модулю. На каком рисунке, показанных на рис.30 правильно показан вектор полного ускорения?

Рис.30

Решение. При движении по криволинейной траектории скорость изменяется по величине и направлению. Составляющая ускорения, характеризующая быстроту изменения скорости по величине, называется тангенциальным ускорением. Она связана с приращением вектора скорости, направленным по касательной к траектории, как и сама скорость. При ускоренном движении тангенциальная составляющая совпадает с вектором скорости, при замедленном - противоположна (как на рис.30.1)

Составляющая ускорения, характеризующая быстроту изменения скорости по направлению, называется нормальным ускорением. Она связана с приращением вектора скорости, направленным перпендикулярно касательной к траектории. Нормальное ускорение всегда направлено к центру кривизны траектории (как на рис. 30.3)

Вектор полного ускорения правильно изображен на рис.30.2.

Пример 16. Угловая скорость точки, движущейся по окружности, изменяется по графику, изображенному на рис.31. Как изменяется со временем угол между векторами ускорения и скорости?

Рис.31

Решение. Согласно графику угловая скорость линейно возрастает. Угловое ускорение по определению равно производной угловой скорости по времени ε=dω/dt.

Производная линейной функции постоянна, поэтому угловое ускорение не изменяется.

Запишем выражения, связывающие составляющие ускорения с угловыми величинами:

Следовательно, тангенциальное ускорение не изменяется по величине в процессе движения, а нормальное ускорение возрастает.

Построим векторы скорости, нормального, тангенциального и полного ускорений. Вектор скорости направлен по касательной к траектории. Направление вектора ускорения рассматривалось ранее.

Рис.32

Из рис.32 видно, что угол α между векторами скорости и ускорения возрастает.

Пример 17. Точка движется, замедляясь, по окружности радиуса R так, что в каждый момент времени ее тангенциальное и нормальное ускорения по модулю равны друг другу. В начальный момент времени t = 0 скорость точки равна v₀. Найти скорость и ускорение точки как функцию времени.

Решение. Установим уравнения, связывающие а_n и а_τ. По условию задачи модули нормального и тангенциального ускорений совпадают: |a_n|=|a_τ|. Нормальное ускорение всегда положительно. При замедленном движении приращение скорости отрицательно. С учетом этих замечаний система уравнений принимает вид

а_n=-а_τ, (1)

Подставляя (2) и (3) в (1), приходим к уравнению с разделяющимися переменными:

Разделяя переменные v и t, получаем

Интегрируем в пределах от t = 0, v = v₀ до t и v(t)

в результате имеем:

Из этого соотношения находим искомую зависимость скорости от времени

Подставляем v(t) в формулу (2)

Учитывая, что a_n=-a_τ и , получаем зависимость полного ускорения от времени:

Пример 18. Материальная точка движется по окружности радиуса R так, что зависимость угла поворота от времени задана уравнением φ=αt³. Найти полное ускорение точки как функцию времени.

Решение. Решим задачу двумя способами.

1 способ. Выпишем формулы соответствующие данному способу.

Выполним указанные в формулах математические действия.

2 способ. Выпишем формулы соответствующие данному способу.

Выполним указанные в формулах математические действия.

Пример 19. Тело, вращаясь равноускоренно с угловым ускорением ε=2 рад/с, имеет в момент времени t₁=2,5 с угловую скорость ω₁=40 рад/с (рис.33). Определить: 1) скорость и ускорение точки тела, отстоящей на расстоянии h=55 см от оси вращения в момент t₂=7 с; 2) число оборотов N тела за время t₃=10 с; 3) уравнение вращательного движения тела, если в начальный момент времени t₀=0 начальный угол поворота φ₀=0.

Рис.33

Решение. 1. При равноускоренном вращении угловая скорость тела изменяется по закону

Зная значение угловой скорости ω₁ в некоторый момент времени t₁ и угловое ускорение ε, можно найти начальную угловую скорость ω₀ (при t₀=0):

Отсюда угловая скорость тела в момент времени t₂=7 с будет равна

Скорость v и ускорение a точки М тела, отстоящей на расстоянии h=55 см от оси вращения, в момент времени t₂ = 7 c будут равны:

Направление векторов скорости и ускорений указаны на рис. 33.

Число оборотов тела за время t₃=10 с определим по соотношению

где n(t) – число оборотов тела за секунду в данный момент времени.

В рассматриваемой задаче

Уравнение вращательного движения тела φ=φ(t) получим из соотношения , умножив обе его части на дифференциал времени dt: . Интегрируя полученное дифференциальное уравнение с учетом начальных условий (t₀=0, φ₀=0):

получим

Вопросы для самопроверки

- Что определяет число степеней свободы твердого тела?

- Сколько независимых параметров нужно задать для определения положения твердого тела: а) свободного; б) с неподвижной точкой; в) с двумя неподвижными точками?

- Дайте определение поступательного движения твердого тела. Каковы свойства этого движения?

- Дайте определение вращательного движения твердого тела вокруг неподвижной оси. Как установить закон вращения?

- Какими кинематическими параметрами характеризуется поступательное движение и почему?

- Запишите уравнение равномерного поступательного движения твердого тела?

- Запишите уравнение равнопеременного поступательного движения твердого тела?

- Запишите уравнение равнопеременного и равномерного вращательного движения твердого тела?

- Почему при поступательном движении тела скорости и ускорения его точек не могут быть различными?

- Сколько степеней свободы имеет тело с двумя закрепленными точками?

- Как найти скорость произвольной точки тела, вращающегося вокруг оси?

- Каковы величина и направление скорости точки тела, вращающегося вокруг оси?

- Приведите определения угловой скорости и углового ускорения тела.

- Как направлены векторы угловой скорости и углового ускорения при вращении тела вокруг неподвижной оси?

- Как вычислить скорость точки тела, вращающегося вокруг неподвижной оси? Объясните куда направлен вектор скорости?

- Запишите формулы для нормального и тангенциального ускорений точки тела, вращающегося вокруг неподвижной оси.

- Опишите картину распределения скоростей точек тела при вращательном движении твердого тела.

- Опишите картину распределения ускорений точек тела при вращательном движении твердого тела.

- Каково геометрическое место точек при вращательном движении твердого тела, скорости которых равны геометрически, равны по модулю?

- Как определить модуль и направление вектора осестремительного ускорения точки при вращении тела вокруг оси?

- Перечислите основные виды движений твердого тела.

- Какое движение твердого тела называется поступательным и какими свойствами оно обладает?

- Какое движение твердого тела называется вращением вокруг неподвижной оси и как оно осуществляется?

- По каким формулам определяются модули угловой скорости и углового ускорения вращающегося твердого тела?

- Как направлены векторы угловой скорости и углового ускорения при вращении тела вокруг неподвижной оси?

- Выведите формулы модулей скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси?

- Запишите векторную формулу линейной скорости точки вращающегося тела.

- Как направляются векторы угловой скорости и углового ускорения при вращательном движении твердого тела?

- При каких условиях ускорение точки вращающегося тела составляет с отрезком, соединяющим точку с центром описываемой ею окружности, углы 0°, 45°, 90°?

- Ускорения каких точек вращающегося тела:

а) равны по модулю;

б) совпадают по направлению;

в) равны по модулю и совпадают по направлению?

- Каковы векторные выражения вращательной скорости, вращательного и центростремительного ускорений?

- Выведите формулы Эйлера для проекций вращательно скорости точки на координатные оси.

- Что представляет собой передаточное число передачи и как определяется передаточное число сложной передачи?

- На какие составляющие движения можно разложить движение свободного тела в общем случае и как они зависят от выбора полюса?

- Как определяют скорости точек свободного твердого тела?

- Как связаны между собой скорости точек свободного тела, расположенных на отрезке произвольного направления, и на отрезке, параллельном мгновенной оси?

- Покажите, что векторы угловой скорости и углового ускорения свободного тела не зависят от выбора полюса.

- Как определяют ускорения точек свободного твердого тела?

- Чему равно число степеней свободы тела с одной закрепленной точкой?

- Приведите названия углов Эйлера.

- Запишите уравнения вращения твердого тела вокруг неподвижной точки.

- Сформулируйте теорему Эйлера-Даламбера.

- Что определяют кинематические уравнения Эйлера?

- Приведите векторную запись формулы для определения линейной скорости точки при вращении твердого тела с одной неподвижной точкой.

- Как определить величину и направление вращательного ускорения точки твердого тела с одной закрепленной точкой?

- Как направлен вектор осестремительного ускорения точки при вращении твердого тела вокруг неподвижной точки?

- Какими параметрами определяется положение твердого тела, одна из точек которого неподвижна?

- Как формулируется теорема Эйлера-Даламбера о перемещении твердого тела, имеющего одну неподвижную точку?

- Что называют мгновенной осью вращения твердого тела с одной неподвижной точкой и каковы уравнения мгновенной оси в неподвижной и подвижной системах осей декартовых координат?

- Что представляют собой неподвижный и подвижный аксоиды мгновенных осей при сферическом движении и что происходит с аксоидами при действительном движении тела?

- Как определяются модуль и направление углового ускорения тела при сферическом движении?

- Почему направления векторов углового ускорения и угловой скорости тела при сферическом движении не совпадают?

- Как определяются скорости точек тела при сферическом движении?

- Какие модули и направления имеют составляющие ускорения точки тела при сферическом движении?

- Почему направления векторов вращательной скорости и вращательного ускорения при сферическом движении тела не совпадают?

- Определите угловую скорость вращения вала электродвигателя (в рад/с), если n=1400 об/мин.? Вычислите скорость и ускорение точки на поверхности вала; диаметр вала d=100 мм?

- Понятие поступательного движения:

1) это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению;

2) если при движении тела какие-либо две точки остаются неподвижными;

3) когда все точки тела перемещаются в параллельных плоскостях;

4) вращение тела вокруг оси;

5) результирующее движение тела.

- Понятие вращательного движения:

1) когда все точки тела совершают одинаковые перемещения;

2) когда все точки тела перемещаются в параллельных плоскостях;

3) когда все точки тела движутся по окружностям, центры которых лежат на одной прямой;

4) вращение самой оси;

5) сложное движение твердого тела.

- Определите характер вращения твердого тела вокруг неподвижной оси в следующих случаях:

1) ε=5 рад/с²;

2) ε=0;

3) ω=150 рад/с;

4) ω=20t рад/с, где t – время?

- Какая составляющая ускорения любой точки твердого тела равна нулю при равномерном вращении твердого тела вокруг неподвижной оси?

1) нормальное ускорение;

2) касательное ускорение;

3) полное ускорение.

- При вращательном движении нормальное ускорение равно

1)

2)

3)

4)

5)

- При вращательном движении угловое ускорение равно

1)

2)

3)

4)

5)

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00