Главная

Олимпиадные задачи по теоретической механике

Олимпиады по теоретической механике, проводимые в технических вузах, а в последнее время и в классических университетах, являются системообразующим элементом организации творческой учебно-познавательной деятельности в высшей школе. Участие студентов в олимпиадном движении способствует более упорядоченному и глубокому усвоению профессиональных знаний, дает возможность сформировать у них готовность к творческой деятельности, развить креативный характер мышления. Все это способствует подготовке конкурентоспособного специалиста, готового к профессиональной деятельности в современных рыночных условиях.

Задача 1

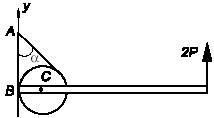
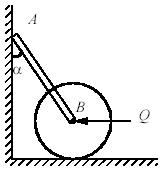
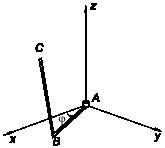
В пространстве движется тонкая пластинка. В некоторый момент времени векторы скоростей двух точек А и В пластинки оказались равными и лежащими в плоскости пластинки, а величина скорости точки С пластинки, являющейся вместе с точками А и В вершинами равностороннего треугольника, в два раза больше скорости точек А и В. Какие точки пластинки имеют в данный момент скорость в два раза большую скорости точки С?

Задача 2

Через неподвижное горизонтально закрепленное бревно переброшена веревка на конце которой находится груз массы m=6кг. Для того чтобы удерживать этот груз другой конец веревки необходимо тянуть с минимальной силой F=40H. С какой минимальной силой надо тянуть веревку, чтобы груз начал подниматься?

Задача 3

На гладкой горизонтальной плоскости находятся три равных однородных жестких стержня длины l, шарнирно соединенных вместе и расположенных по одной прямой. Два внешних стержня приводятся во вращение относительно концов среднего стержня с равными угловыми скоростями w в противоположных направлениях. Как будет двигаться треугольник, образованный стержнями после удара двух внешних стержней?

Задача 4

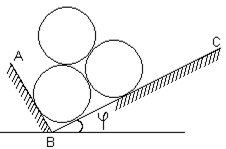
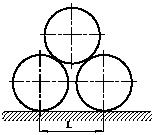
Три гладких однородных одинаковых цилиндра опираются на две взаимно перпендикулярные плоскости АВ и ВС. Каков наименьший угол наклона f плоскости ВС, при котором система сохраняет равновесие?

Задача 5

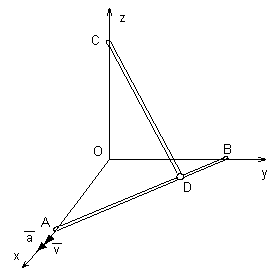
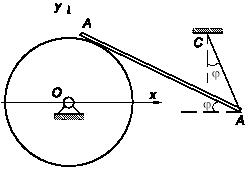
Два стержня АВ и СD одинаковой длины l скреплены в точке D шарнирно. Концы стержней А, В и С скользят вдоль соответствующих осей прямоугольной системы координат xyz. Определить скорость и ускорение точки С стержня CD и величину его угловой скорости, полагая, что вращение стержня вокруг оси CD отсутствует. Известны: скорость v и ускорение a точки A. BD = 0,25l, а также угол OAB в расчетном положении, равный 60⁰.

Задача 6

Однородный стержень AB покоился на гладкой горизонтальной плоскости в момент, когда в точке B об него ударился шарик D (материальная точка массой m). Скорость шарика перед соударением была направлена горизонтально и перпендикулярно к стержню. При каком коэффициенте восстановления k стержень ударит вторым концом по шарику D, если масса стержня 4m?

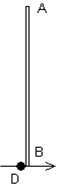
Задача 7

Диск радиуса r катится внутри цилиндрической полости радиуса R, прижимая тонкий обруч радиуса p (r< p< R), как показано на рисунке. Проскальзывание при движении отсутствует. Найти угловую скорость обруча, если линейная скорость центра диска равна v₀.

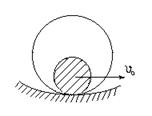
Задача 8

Тележка А скатывается с постоянной скоростью по прямолинейному наклонному пути, сматывая трос с барабана и заставляя последний вращаться. Найти зависимость между длиной пути x, пройденного тележкой из состояния покоя A₀ и угловой скоростью ω_x вращения барабана.

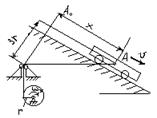
Задача 9

Небольшой брусок массой m, находившийся на абсолютно гладкой полусфере радиусом r в положении A₀, получив начальную скорость V₀, соскальзывает по ней. При каком φ брусок оторвется от полусферы?

Задача 10

Круглая горизонтальная платформа может вращаться без трения вокруг вертикальной оси, проходящей через ее центр. Человек начинает движение от края платформы со скоростью v и, выдерживая эту скорость постоянной, движется по диаметру платформы. Какую работу совершит человек на пути от края платформы до ее центра? Момент инерции платформы относительно оси вращения равен J, радиус R, ее начальная угловая скорость ω₀. Человека считать точечной массой m. Рассмотреть движение человека в системе отсчета, связанной с вращающейся платформой, и указать условия, при которых скорость человека будет постоянной.

Задача 11

Дельфин массой m выпрыгивает из моря под углом α к горизонту и поднимается в воздух на высоту h. Определить силу тяги Т, развиваемую дельфином в воде, предполагая эту силу постоянной. Считать, что дельфин движется по воде ∆t секунд из состояния покоя при постоянной силе сопротивления R. Вес дельфина в воде G уравновешивается архимедовой силой поддержания P; при движении дельфина над морем сопротивлением воздуха пренебречь.

Задача 12

По шероховатой наклонной плоскости, образующей угол α с горизонтом, катятся примыкая друг к другу вещественно симметричные цилиндры А и В, имеющие одинаковые радиусы r и одинаковые массы m, но различные моменты инерции относительно осей симметрии: mr² - для цилиндра B и Vmr² - для цилиндра А, где 0< V< 1. По плоскости цилиндры катятся без скольжения. Коэффициент скольжения между цилиндрами равен f. Определить ускорение w центров, а так же давление N цилиндра А на цилиндр В. Определить tgα₀, где α₀ - наибольший угол наклона плоскости, при котором еще возможно качение катков без скольжения. Коэффициент трения скольжения шаров по плоскости считать равным коэффициенту трения скольжения шаров между собой.

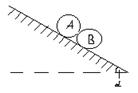
Задача 13

Путешественники застрелили в Африке напавшего на них крокодила. Они захотели измерить его длину, но у них не оказалось необходимого инструмента — рулетки, сантиметра, линейки. Как определить длину крокодила с высокой точностью, используя измерительный прибор, обычно имеющийся у путешественников, не предназначенный для определения длины?

Задача 14

На внутренней стенке закрытой банки, уравновешенной на чувствительных весах, сидит муха. Что произойдёт с весами, если, покинув своё место, муха станет летать внутри банки?

Задача 15

На самолёт установили реактивный двигатель, развивающий определённую силу тяги, не зависящую от скорости. Сила тяги оказалась мала, поэтому на самолёт установили второй, точно такой же реактивный двигатель. Во сколько раз при этом увеличилась полезная мощность силовой установки?

Задача 16

Компания отправилась на автомобиле на загородную прогулку. После недавнего дождя дорога размокла и автомобиль увяз в выбоине. Один из молодых людей утверждает, что достаточно силён, что бы в одиночку вытащить машину из грязи и девушки могут не опасаться за чистоту своих туфель. С этой целью он привязывает один конец длинной верёвки к автомобилю, туго натягивая верёвку другой её конец привязывает к дереву, и начинает тянуть верёвку за её середину под прямым углом к её направлению. Сможет ли молодой человек совершить обещанное?

Задача 17

Самолёт летит по замкнутому маршруту Волгоград — Никудыкино — Волгоград на побитие рекорда скорости.

а) На протяжении всего полёта ветер дует по направлению Волгоград — Никудыкино с постоянной скоростью. Улучшится или ухудшится рекорд из-за ветра? 

б) На протяжении всего полёта ветер дует перпендикулярно направлению Волгоград — Никудыкино с постоянной скоростью. Улучшится или ухудшится рекорд в этом случае?

Задача 18

Прыгун на Земле преодолевает высоту 2 м. Центр масс спортсмена находится на высоте 1,2 м, перед прыжком спортсмен приседает на глубину приседания (длину толчка) 0,35 м. Какую высоту этот прыгун может взять на Луне, где сила тяжести в 6 раз меньше?

Задача 19

С вершины башни брошены с одинаковой скоростью четыре камня: один - отвесно вверх, второй - отвесно вниз, третий - горизонтально вправо, четвёртый - горизонтально влево. Какую форму имеет тот четырёхугольник, в вершинах которого будут находиться камни во время падения?

Задача 20

Двое рабочих несут тяжело нагруженные носилки. Один из них выпускает ручки, и носилки начинают падать. Увеличится или уменьшится нагрузка на второго рабочего?

Задача 21

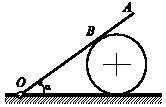
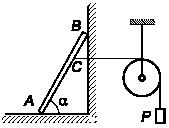
Тяжелая балка ОА, закрепленная одним концом в шарнире О, опирается в точке В на шар весом Р, лежащий на неподвижной горизонтальной плоскости. Определить угол α при равновесии, если коэффициент трения шара о балку и горизонтальную плоскость одинаков и равен f.

Задача 22

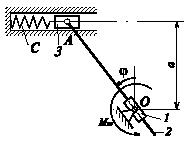
В плоском механизме звенья невесомы, связи идеальные. К цилиндру 1 приложен известный момент M_вр, пары сил. Найти величину деформации пружины, если жесткость пружины равна с и механизм в указанном на рисунке положении, определенном углом φ, находится в покое. Стержень 2 может свободно скользить в цилиндре 1.

Задача 23

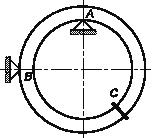
Однородное кольцо весом Р свободно опирается в точках А и В на неподвижные призмы, которые расположены соответственно на вертикальном и горизонтальном диаметрах кольца. Считая коэффициенты трения кольца о призмы одинаковыми, определить такое их значение, при котором точечный груз С весом Q, закрепленный в любом месте правой половины кольца, будет оставлять последнее в покое. Поперечными размерами кольца пренебречь.

Задача 24

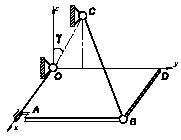
Тяжелая тонкая однородная прямоугольная плита OABD весом Q удерживается в горизонтальном положении сферическим шарниром О, цилиндрическим шарниром А и тонким тяжелым стержнем СВ весом Р. Стержень прикреплен сферическими шарнирами к плите в точке В и к вертикальной стене в точке С. Считая трение во всех шарнирах пренебрежимо малым и угол γ известным, найти составляющую реакции цилиндрического шарнира А, параллельную оси Оу, используя принцип возможных перемещений. Полученное решение проверить с помощью уравнений статики.

Задача 25

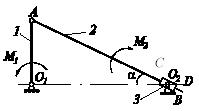
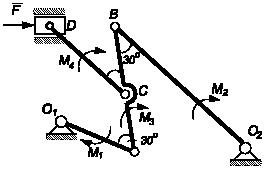
В плоском механизме на кривошип О₁А действует пара сил с известным моментом M₁. Найти минимальное значение момента М₂ пары сил, приложенной к звену 3 и обеспечивающей равновесие механизма в указанном на рисунке положении, если АО₁О₂ = 90°, O₁O₂A = α, O₁A = r, CO₂ = O₂D = a, коэффициент трения между стержнем 2 и втулкой 3 равен f, трение в шарнирах О₁, А, О₂ пренебрежимо мало, все звенья механизма невесомые, контакт стержня 2 со втулкой 3 имеет место только в точках С и D.

Задача 26

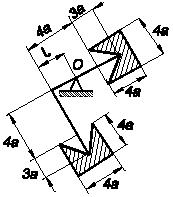
Жесткая конструкция, состоящая из двух одинаковых тяжелых однородных пластин, соединенных тонким изогнутым под прямым углом стержнем пренебрежимо малого веса, удерживается в равновесии на опоре О. Считая коэффициент трения стержня об опору равным f, найти максимальное значение l, при котором тело будет удерживаться на опоре в равновесии. Размеры и форма пластин показаны на рисунке.

Задача 27

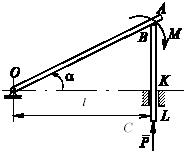
В плоском механизме стержень OA может вращаться вокруг шарнира O, перемещая шток ВС в идеально гладких направляющих KL. Расстояние между шарниром и направляющими - l. Поверхность контакта между стержнем и штоком в точке В - шероховатая, коэффициент трения скольжения - f. Найти минимальное значение момента M пары сил, действующей на стержень ОА и обеспечивающей равновесие механизма при заданных значениях угла α и силы Р. Весом стержней пренебречь.

Задача 28

Плоский механизм с невесомыми звеньями находится в равновесии. Момент М пары сил, приложенной к звену ОАВ, уравновешен силой упругости пружины. Показать, что абсолютная величина силы упругости пружины при данном положении механизма может определяться равенством F_упр=M∙SK/(LK∙OS), AS⊥AE, ES⊥OC, AE∥OC.

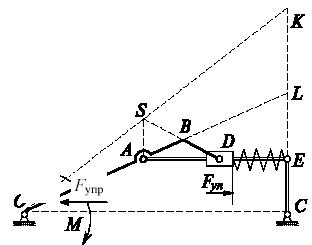
Задача 29

Определить усилие S в стержне АВ плоской фермы, закрепленной и нагруженной, как указано на рисунке.

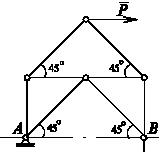
Задача 30

Цилиндр 1 веса Q₁ опирается на два одинаковых цилиндра веса Q₂, как показано на рисунке. Коэффициент трения скольжения между цилиндрами равен f. Определить максимальный угол α и минимальный коэффициент трения f₀ между цилиндрами 2 и 3 и опорной поверхностью.

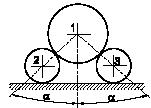
Задача 31

К твердому телу приложены две пары сил с моментами m₁ и m₂, расположенными в плоскостях A₁x+b₁y+C₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0 соответственно. Определить проекции момента m результирующей пары на координатные оси.

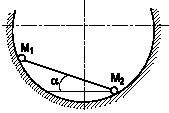
Задача 32

Две тяжелые точки M₁ и М₂ соединены между собой невесомым жестким стержнем, находящимся внутри гладкой сферы. Длина стержня и радиус сферы равны. Определить при равновесии угол α между стержнем и горизонтом, если масса точки M₂ в два раза больше массы точки М₁.

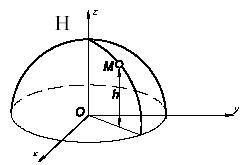
Задача 33

Поверхность параболического купола описывается уравнением z=H-(x²+y²)/H. На высоте h на купол был положен груз. При каких значениях h возможно равновесие груза, если коэффициент трения между грузом и куполом равен f ?

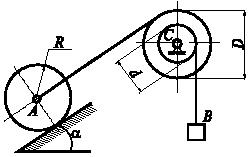
Задача 34

Цилиндр веса Q и радиуса R лежит на шероховатой плоскости, наклоненной к горизонту под углом α, и удерживается тросом, намотанным на барабан ступенчатого вала диаметра D. На барабан диаметра d намотан трос, к концу которого подвешен груз веса Р. Коэффициент трения качения цилиндра А о плоскость равен δ, коэффициент трения скольжения равен f, при этом tgα>δ/R, f>δ/R. При каких значениях Р система будет находиться в равновесии?

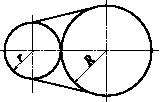
Задача 35

Два диска радиусами R и r, расположенные на горизонтальной плоскости, стянуты упругой нитью жесткостью c. Диски давят друг на друга с силами, равными Q. Как изменится длина нити, если ее перерезать?

Задача 36

Главные моменты некоторой системы сил относительно центров О, А и В одинаковы по величине M₀ = M_A = M_B = m. Главный вектор этой системы сил по величине равен V и параллелен оси z; ОА=а, ОВ=b. Определить углы, составляемые главными моментами M₀, M_A, M_B с плоскостью хоу.

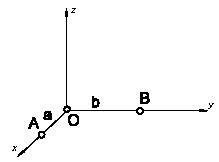
Задача 37

Тонкий однородный стержень ОА длины l концом O закреплен шарнирно на высоте h над горизонтальной поверхностью жидкости, в которую опущен второй его конец. Плотность жидкости равна ρ, плотность стержня kρ (k и ρ - постоянные). Определить значения угла φ при равновесии стержня. Исследовать устойчивость положений равновесия.

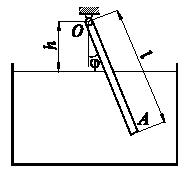
Задача 38

Однородный диск весом Р и радиусом R удерживается в равновесии с помощью невесомой нити, концы которой прикреплены к потолку. Найти натяжение нити и удельное давление (давление на единицу длины нити) на нить в функции угла α на участке АСВ. Ветви нерастяжимой нити AA₁ и ВВ₁ вертикальны, трение не учитывать.

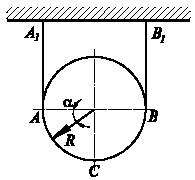
Задача 39

Однородная равносторонняя пластинка веса Р стороной AB=l опирается на горизонтальный пол ХОУ, ее стороны АС и ВС касаются стен ХОZ и YОZ . Пренебрегая трением, определить силу F, удерживавшую пластинку в равновесии.

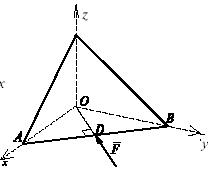
Задача 40

На верхней грани прямоугольного бруса А веса P₁ находится прямоугольный брус В веса Р₂. Брус А опирается нижней гранью на горизонтальную плоскость, причем коэффициент трения между ними равен f₁. Коэффициент трения между брусками А и В равен f₂. К брусу В приложили силу под углом α к горизонту. При каких значениях силы F система будет оставаться в равновесии?

Задача 41

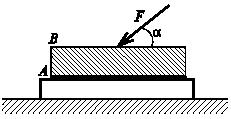
Конец О ломаного стержня ОАВС жестко защемлен. Стержень нагружен крутящим моментом М_кр, парой сил с моментом M, расположенной в плоскости УОZ, и силой F. Сила F расположена в плоскости Х₁CY₁ (X₁ || X, Y₁ || Y) и составляет с осью Y₁ угол α= 60°. Определить модуль реактивного момента заделки, если ОА = а, АВ = в, ВС = с. Проведите вычисления при а = 1 м, в = 2 м, с = 0,5 м, F = 2 H, М_кр =0,5 Hм, M = 1 Нм.

Задача 42

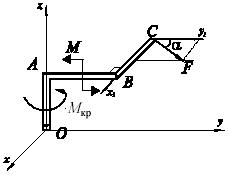
В антипараллелограмме О₁АВО₂ длины звеньев равны соответственно О₁А = О₂В = а, АВ = О₁О₂ = в (в > а). Механизм находится в равновесии под действием вращающихся моментов М₁ и М₂, приложенных к звеньям О₁А и О₂В. Определить отношение М₂/М₁, если O₂B⊥O₁O₂.

Задача 43

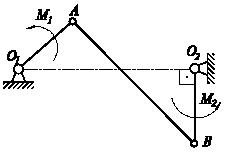
Призма В опирается на клин А и вертикальную стену. Массы призмы и клина одинаковы. Трение между клином и призмой пренебрежимо мало. Коэффициенты трения между клином и полом, призмой и стеной одинаковы и равны f. Наклонная плоскость клина составляет с горизонтом угол α. При каких значениях f призма и клин будут оставаться в покое?

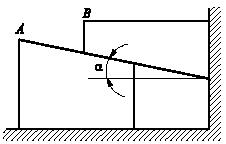
Задача 44

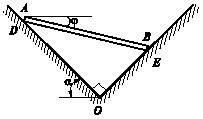
Концы расположенного в вертикальной плоскости тяжелого однородного стержня могут скользить в прорезях взаимно перпендикулярных плоскостей ОD и ОЕ. Плоскость ОD составляет с горизонтом угол α. Пренебрегая трением, определить значение угла φ при равновесии стержня. Будет ли положение равновесия стержня устойчивым?

Задача 45

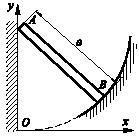
Однородный стержень длины а опирается одним концом А на гладкую вертикальную стенку, другим В - на гладкий профиль, расположенный в вертикальной плоскости. Какова должна быть форма профиля, чтобы стержень мог оставаться в покое в любом положении?

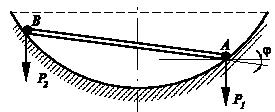
Задача 46

Система, состоящая из двух шаров А и В с весами Р₁ и Р₂ (Р₁ > P₂) и соединяющего их невесомого стержня длиной l, помещена в сферическую чашу радиуса r=0,5l, коэффициент трения скольжения шаров о поверхность чаши равен f. Найти наименьшее значение угла φ между стержнем и горизонтом, при котором система может находиться в покое внутри чаши. Размерами шаров пренебречь.

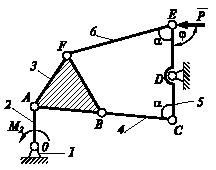
Задача 47

Определить момент пары M₂, уравновешивающий механизм в данном его положении, и реакции в шарнирах С, D и Е рычага 5. Шарнир В находится на прямой АС. Дано: ОА = СЕ = l, CD = 0,5l, α= 60°, φ= 90°; внешняя сила Р.

Задача 48

Шестерня напрессована на вал и сила трения между ними, вызванная напрессовкой, равна Q, коэффициент трения сцепления равен f₀. Определить закон изменения силы Р = f(y), которую нужно приложить для снятия шестерни с вала.

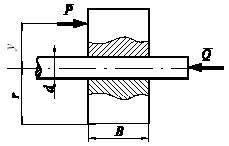
Задача 49

Жесткая стержневая фигура опирается равномерно полуокружностью на негладкую горизонтальную плоскость. Пренебрегая весом фигуры и трением в подшипниках А и В, определить для случая покоя наибольший движущий момент М и соответствующие реакции опор, если даны: радиус R, вертикальная сила Q и коэффициент сцепления f, (OA = AB = R).

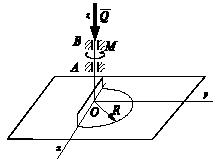
Задача 50

В плоском кулисном механизме ползуны А и В могут перемещаться вдоль стержней кривошипа DOE. Пренебрегая трением и весом звеньев механизма, определить силу Q, уравновешивающую действие момента M, АВ = ВС = l.

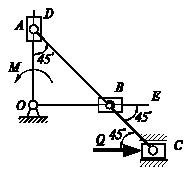
Задача 51

Однородная цепь веса Р и длины 2πR перекинута через гладкий блок, имеющий горизонтальную ось. Определить в случае равновесия силу натяжения цепи в ее произвольном поперечном сечении.

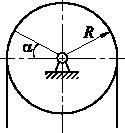
Задача 52

Механизм, расположенный в горизонтальной плоскости, состоит из двух зубчатых колес и стержней, связанных шарнирами. Считая связи идеальными, определить величину силы F, уравновешивающей действие момента М. Радиус левого колеса R .

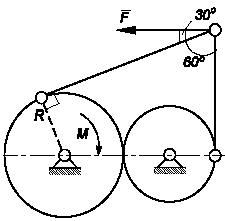
Задача 53

К равностороннему трехшарнирному звену ВСD приложена сила Р. Определить уравновешивающий момент М₁ механизма. Размеры стержней одинаковы и равны l, КВ = КС = 0,5l; ОА, CF, перпендикулярны BD.

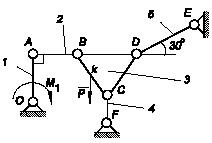
Задача 54

При какой минимальной тормозной силе Р и жесткости пружины c будет тормозиться и растормаживаться диск 1, на который действует постоянный момент внешних сил М = 600 Нcм? Для соприкосновения тормозной колодки с диском пружину нужно растянуть на величину h = 1 см. Коэффициент трения в точке A f = 0,3, трение в шарнирах не учитывать. Размеры механизма: r = 10 см, a = 4 см, b = l = 20 см, α = 90°, β = 45°.

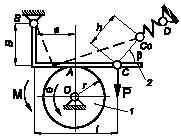
Задача 55

Однородный стержень АВ весом G опирается на шероховатые горизонтальную и вертикальную плоскости. Угол α и коэффициент f трения таковы, что стержень не находится в равновесии. Определить величину и положение наименьшей силы Pmin, которая должна быть приложена в центре тяжести стержня для того, чтобы стержень в данном положении был неподвижным.

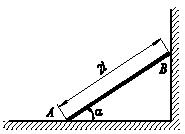
Задача 56

Плоский угольник состоит из двух одинаковых тонких однородных стержней. Стержни жестко соединены между собой в вершине D под углом 90°. Угольник установлен на неподвижную горизонтальную шероховатую цилиндрическую опору радиуса r, коэффициент трения скольжения f0 = 0,268. Угольник поворачивают по часовой стрелке на угол α из начального положения А0B0, останавливают и затем освобождают без толчка. После освобождения угольника возможны два случая: 1) в точке B стержень соприкасается с опорой, 2) в точке В между стержнем и опорой имеется небольшой зазор ∆l<<r. Опишите качественно дальнейшее движение угольника после его освобождения и определите предельные значения угла α, при которых угольник будет иметь различные состояния равновесия - безразличное, устойчивое, неустойчивое. Сопротивлением перекатывания пренебречь.

<<

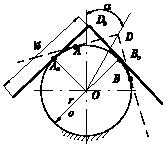
Задача 57

В паз шириной b помещена негладкая призма весом G, сечение которой - равнобедренный треугольник с углом α при вершине С. К призме приложена пара сил с моментом М и наименьшая уравновешивающая сила Р, перпендикулярная силе G и параллельная оси x, при которой призма будет находиться в покое. Определить реакцию связи и силу Р. Дано: коэффициент трения f, α=4φ, tgφ=f, M = bG, h = 3/2 f b.

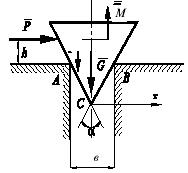
Задача 58

Клин равномерно перемещается вертикально вниз, касаясь гладкой стены и шероховатой поверхности катка. Каток при этом может перемещаться по негладкой горизонтальной плоскости. Исследовать влияние угла α клина и коэффициента трения скольжения f связях А и В на характер движения цилиндрического катка. Силу NA, перпендикулярную к стороне АС клина, считать постоянной, каток невесомым.

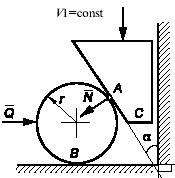
Задача 59

Цилиндр 2 веса Q и радиуса r соединен шарнирным невесомым стержнем O1O2 длиной 2r с опорой O1; к оси О1 прикреплен на нити груз 3. Механическая система находится в равновесии; при этом вертикальная прямая O1A делит угол β пополам. Определить вес Р груза 3.

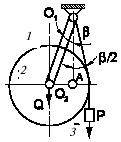
Задача 60

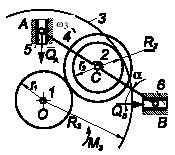
Определить величину момента МЗ, при котором зубчато-рычажный механизм в данном положении будет находиться в равновесии. Массами тел и трением в связях пренебречь. Дано: АС = ВС = l, r₁ = R₂ = 0,5l, r₂ = 0,25l, угол α = 30°, угол АОВ = 90°, угловая скорость ω₃ = 0, сила QA = QB = Q.

Задача 61

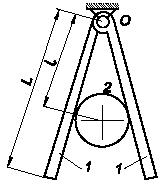
Шар 2 веса G2 и радиуса r удерживается силами трения между одинаковыми пластинками 1 веса G1 каждая, шарнирно подвешенными на горизонтальной оси O. Поперечными размерами пластин пренебречь. Длина пластины равна L, расстояние от оси O до точки касания пластины с шаром - l, коэффициент трения между шаром и пластиной - f. Считая заданными указанные геометрические размеры, найти условия, которым должны удовлетворять величины f, G1, G2 при равновесии системы.

Задача 62

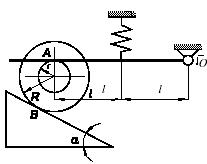
Определить деформацию λ пружины жесткостью c для системы, изображенной на рисунке в положении предельного состояния равновесия. Исходные данные: отношения радиусов двухступенчатого катка r/R = 0,2, коэффициент сцепления в точках А и В контакта катка с горизонтально расположенным невесомым стержнем ОЕ и наклоненной к горизонту под углом α= 30° плоскостью f = 0,577, отношение коэффициента трения качения катка в точке В к большему радиуса катка k/R = 0,5, вес катка равен Q, в точке O - шарнир.

Задача 63

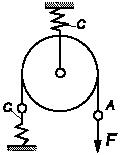
На сколько переместится конец перекинутой через подвижный блок нити (точка А), если к нему приложить силу F? Жесткость пружины с.

Задача 64

Три невесомых стержня, расположенных в вертикальной плоскости, опираются на цилиндр радиуса r. Средний стержень длиной r - горизонтален, боковые стержни имеют одинаковую длину l. Определить давление среднего стержня на цилиндр в зависимости от длины l боковых стержней, если к их концам приложены одинаковые силы Р, направленные вертикально вниз.

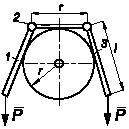
Задача 65

Однородные стержни 1 и 2 одинаковой длины с массами m₁ и m₂, расположенные в вертикальной плоскости, соединены идеальным шарниром С, а концами А и В опираются на шероховатую плоскость. Коэффициент трения между стержнями и полом равен f. Определить наименьший угол α наклона стержней к горизонту в состоянии равновесия.

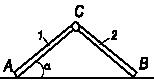
Задача 66

Главные моменты системы сил относительно центров O, А, В направлены как указано на чертеже и равны по величине: M_O = М, M_A = 4M, M_B = 5M. Докажите, что система сил приводится к равнодействующей, определите модуль равнодействующей.

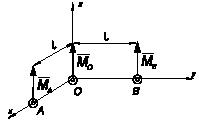
Задача 67

Цепь, состоящая из n одинаковых стержней, подвешена в вертикальной плоскости. Р - вес одного стержня; Q – заданная горизонтальная сила; O, А₁, А₂, ... А_n - шарниры. Найти углы φ_k (к = 1, 2, ..., n) стержней с вертикалью в положении равновесия.

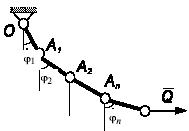
Задача 68

Треугольная пластина весом Р лежит на наклонной плоскости и опирается на нее шаровой катковой опорой А и двумя штырями В и C. Коэффициенты трения скольжения штырей В и С о плоскость соответственно f1 и f2 (f1 < f2). Определить угол α, при котором пластина потеряет равновесие, СА || MN.

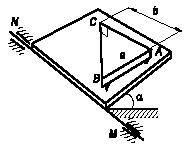
Задача 69

Главные моменты системы сил относительно центров O и А равны М_O и М_A и направлены как указано на чертеже. Докажите, что система сил не имеет равнодействующей. Определите проекцию главного вектора системы на плоскость ХОZ.

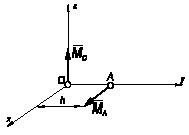
Задача 70

Цилиндр веса Р опирается на два одинаковых параллелепипеда того же веса. Радиус цилиндра r и размеры параллелепипедов а и h заданы. Коэффициент трения между параллелепипедами и горизонтальной плоскостью равен f. Каким условиям должно удовлетворять расстояние b между параллелепипедами для того, чтобы система находилась в равновесии? Трением между цилиндром и параллелепипедами пренебречь.

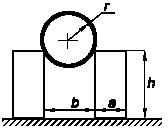
Задача 71

Сформулировать в аналитической форме условие, при котором две силы Р₁ (Р_1X, Р_1Y, Р_1Z) и Р₂ (Р_2X, Р_2Y, Р_2Z), приложенные соответственно в точках А₁ (а₁,в₁,с₁), А₂ (а₂,в₂,с₂), лежат в одной плоскости.

Задача 72

Конструкция, изображенная на рисунке, состоит из четырех одинаковых стержней массы M и длины l каждый, соединенных шарнирами и расположенных в вертикальной плоскости. Шарниры D и B соединены пружиной. В состоянии равновесия стержни образуют квадрат. Определить жесткость c пружины, если в ненапряженном состоянии она имеет длину 2l.

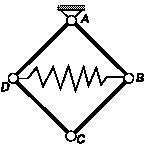
Задача 73

Стержни СА, СВ и СD одинаковой длины соединены в точке С сферическим шарниром, концами А, В, D опираются на гладкую горизонтальную плоскость. Середины стержней А1, В1, D1 соединены нитями, длины которых в два раза меньше длин стержней. Определить натяжение нитей, если стержни однородные и масса каждого равна М.

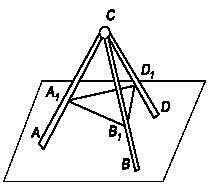
Задача 74

Однородная балка АВ весом Р и длиной 4а прикреплена к вертикальной стене сферическим шарниром А и удерживается перпендикулярно стене невесомыми растяжками DЕ и GС, причем DЕ лежит в горизонтальной плоскости, а GС составляет с этой плоскостью угол α. К концу В балки подвешен груз M весом Q. Определить реакцию шарнира А и натяжение растяжек, если АЕ = AD = DC = а, АF = 2а.

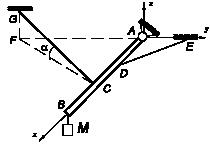
Задача 75

Кривошипно-ползунный механизм, расположенный в вертикальной плоскости, находится в равновесии в указанном на рисунке положении. Вес стержней ОА и АВ одинаков, ползун В - невесомый, опирается на шероховатую поверхность 1-1. Определить, коэффициент трения скольжения между ползуном и поверхностью 1-1, пренебрегая трением в шарнирах.

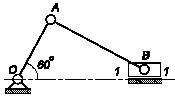
Задача 76

Катушка весом G, радиусами r и R удерживается в равновесии при помощи нити и негладкой вертикальной стены. Определить наименьший коэффициент трения f между катушкой и стеной, если угол α = 30° и r/R = 0,2.

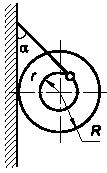
Задача 77

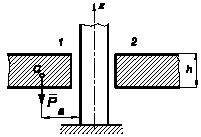
По вертикальному столбу 1 скользит пластина 2 толщины h с круглым отверстием. Определить наименьшую силу тяжести Р и наименьшее расстояние а между центром тяжести С пластины и осью столба при условии равновесия пластины за счет сил трения. Коэффициент трения между столбом и пластиной равен f.

Задача 78

Однородный стержень АВ веса G опирается одним концом на гладкий пол, другим на шероховатую вертикальную стену; коэффициент трения стержня о стену равен f. Определить наибольший и наименьший вес груза Р, чтобы стержень оставался в равновесии, если АС = ВС, угол наклона стержня к горизонту равен α.

Задача 79

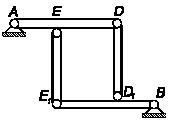
Конструкция состоит из двух балок АD и BЕ1 одинаковой длины соединенных между собой посредством двух шарнирных стержней ЕЕ1 и DD1. Масса балки BЕ1 в два раза больше массы балки АD, расстояние ЕD = Е1D1 = 1/3 Е1В. Определить усилия в стержнях и реакции опор А и В при равновесии системы.

Задача 80

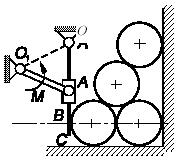
Вертикальная плита ОС удерживает в равновесии четыре одинаковые горизонтально лежащие трубы весом Р каждая. Найти минимальную величину момента M, приложенного к рычагу О1А длиной r при условии, что ∠AO₁O=π/2, ∠AOO₁=π/6, OB=2r.

Задача 81

Два груза А и В, связанные невесомой нерастяжимой нитью АСВ, могут двигаться по вертикальным направляющим, расстояние между которыми равно а. Коэффициент трения в направляющей груза А равен f, а трением в направлявшей груза В можно пренебречь. Каковы пределы изменения расстояния x=DА, в которых возможно равновесие системы, если груз В в n раз тяжелее груза А? Размерами идеального блока С можно пренебречь.

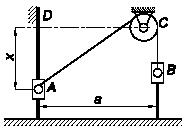
Задача 82

Концы тонкого тяжелого однородного стержня АВ длины l = 4 м могут скользить по гладкой параболе y = 0,5x². Определить значения угла φ при равновесии.

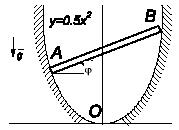
Задача 83

Заделанный в стену горизонтальный стержень AB соединен со стержнем СD скользящим шарниром С. К середине СD приложена горизонтальная сила Р, на стержень АВ действует пара сил с моментом М и вертикальная сила Q. Определить реакции в заделке и шарнире С, если Р= 4 Н; М = 12 Hм; Q = 16Н; a = 1 м.

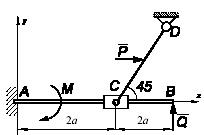
Задача 84

Тяжелая гибкая нить АСВ, закрепленная в точках А и В, как показано на рисунке, находится в равновесии. В некоторый момент времени к нити в точке С подвешивают груз М, переводящий нить в новое положение равновесия, обозначенное на рисунке пунктиром. Куда переместится при этом центр тяжести нити? Дайте обоснование ответа.

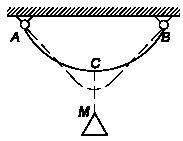
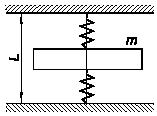
Задача 85

Тонкая пластинка массы m зажата между двумя вертикальными пружинами. Длина каждой пружины в свободном состоянии равна l. Под действием силы Р верхняя пружина сжимается на ∆₁, нижняя - на ∆₂. Определить положение пластинки при равновесии.

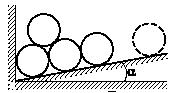
Задача 86

При каком минимальном количестве одинаковых труб нижнего ряда система не раскатится, если не учитывать трение? Угол α = 2°.

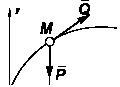
Задача 87

К точке M весом Р, находящейся в равновесном положении x = x0 на шероховатой кривой y = sin (x) приложена сила Q, направленная по касательной к кривой вверх. Определить модуль этой силы, если коэффициент трения f < (dy/dx)(x₀).

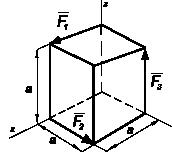
Задача 88

Какую наименьшую по величине и параллельную оси OX силу Q надо приложить к кубу, чтобы система четырех сил F1, F2, F3, Q имела равнодействующую? Считать F1 = F2 = F3 = F.

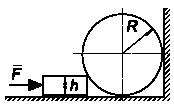
Задача 89

Гладкий шар радиуса R и веса P, касаясь вертикальной стены, покоится на шероховатом горизонтальном полу (коэффициент трения скольжения равен f). С какой минимальной по величине силой F следует прижать к шару брусок высоты h, чтобы шар оторвался от пола?

Задача 90

Между неподвижными телами А и В установлены два клина 1 и 2. Грани клина 1 и поверхность тела А гладкие. Вертикальная грань клина 2 гладкая, а наклонная грань и поверхность тела В шероховатые. При каком значении коэффициента трения f между поверхностями контакта клина 2 и тела В наступит момент предельного равновесия, если давить на клин 1 силой Р? Считать, что силы давления клина 2 на тело В распределяются по его поверхности равномерно.

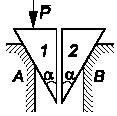
Задача 91

Написать зависимости, определяющие положение равновесия системы двух одинаковых воздушных шаров, показанной на рисунке. Р - подъемная сила каждого шара, R1 и R2 - силы давления ветра на шары, зависящие, от высоты y_i : R_i = R₀ + k₀ y_i, где R₀ и k₀ - постоянные. Расстояния от точки Х₀ до центра первого шара и между центрами шаров равны l₀. Весами тросов и силами давления ветра на них пренебречь.

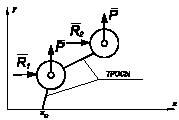
Задача 92

Для конструкции, показанной на рисунке, определить реакции опор А и В и усилия взаимодействия во втулке, допускающей относительное скольжение без трения вдоль АС. Р = 12,0 кН. Стержни АС и ВС, а также блок Е и нить DЕF считать невесомыми. Размеры блоков не учитывать.

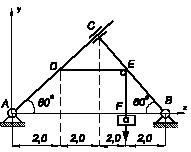
Задача 93

Однородный тяжелый стержень OВ шарнирно закреплен в точке О и удерживается в равновесии в вертикальной плоскости невесомым тросом АВС. Считая угол φ известным, найти условие, которому должны удовлетворять углы α и β, если трение между тросом и стержнем в точке В отсутствует.

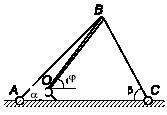
Задача 94

В системе, состоящей из n балок, каждая из последующих опирается левым концом на предыдущую балку, а правым - на шарнирно-неподвижную опору. К каждой балке приложена сила Р в середине пролета l. Определить реакцию опоры А.

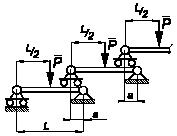
Задача 95

Система состоит из трех сил: F1, F2, F3, приложенных к вершинам О, В, D пирамиды. При каком значении ОА = ВС = b угол между главным вектором и главным моментом данной системы будет равен 120° ? F1 = F2 = F3 = P, AB = OC = OD = a.

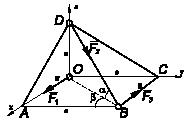
Задача 96

Система состоит из n одинаковых горизонтальных стержней весом Р каждый, укрепленных при помощи тросов. Найти натяжение троса А1К, если С1В1 / А1В1 = С2В2/А2В2 = … = СnВn/АnВn = 1/4.

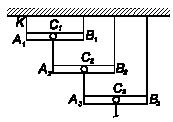
Задача 97

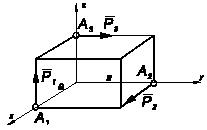
На тело действуют три силы: приложенные в точках А1(а, 0, 0), А2(0, в, 0), А3(0, 0, с), соответственно. Какой должна быть зависимость между а, в и с, чтобы система сил приводилась к равнодействующей?

Задача 98

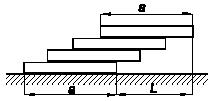
Гладкие однородные бруски одинакового веса и длины уложены так один на другой, как показано на рисунке. Найти такую максимальную длину L (как функцию от числа n брусков), чтобы система n брусков оставалась в состоянии покоя.

Задача 99

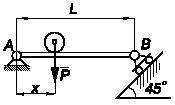
Шарнирная опора А балки не закреплена, а установлена на шероховатую плоскость с коэффициентом трения f. Шарнирно-подвижная опора В расположена на наклонной плоскости под углом 45° к горизонтали. Определить точку приложения силы Р (абсциссу x), при которой возможно смещение опоры А. Вес балки 2Р. Чему должны равняться f и x для того, чтобы в предельном равновесии балки вертикальные составляющие реакций опор А и В были бы одинаковыми?

Задача 100

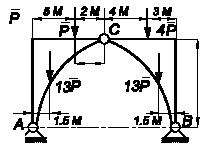
С помощью принципа возможных перемещений определить горизонтальную составляющую реакции в шарнире С.

Задача 101

Плоская система состоит из однородного стержня ОА длиной a и весом Q и груза M весом Р, соединенных нитью АВM длиной l. Найти уравнение кривой ВМС в координатах r и φ (r = ВМ), чтобы при любом угле α<φ система находилась в равновесии; ОА = ОВ; l=a. Трением пренебречь.

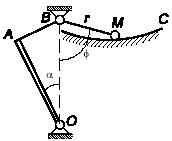
Задача 102

Тонкий однородный стержень АВ веса Р, который наклонен к горизонту под углом α , опирается на неподвижные призмы. Коэффициент трения стержня о призмы f. Какова должна быть длина стержня l, чтобы он находился в равновесии, если СЕ = a, ВС = b?

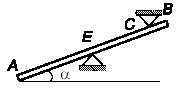
Задача 103

В цилиндрическое отверстие тела А радиуса R = 3r вставлены без натяга шесть цилиндров радиуса r и веса Q каждый. Определить давление цилиндра 4 на стенку отверстия в точке их контакта. Система расположена в вертикальной плоскости.

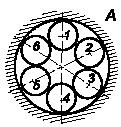
Задача 104

Кольцо радиуса R состоит из трех одинаковых дуг АВ, ВС и СА, соединенных между собой шарнирами. К каждой из дуг на равных расстояниях от шарниров в плоскости кольца приложены силы Р_i, линии действия которых проходят через центр O; кольцо расположено в горизонтальной плоскости. Определить реакции в шарнирах А, В и С. Принять P1 = P2 = P3 = Р.

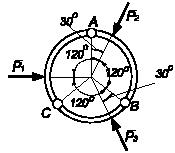
Задача 105

Два клина А и В, коэффициент трения между которыми равен f, могут двигаться без трения в своих направляющих. К клину А приложена сила Р. Какую силу Q нужно приложить к клину В, чтобы клин А двигался равномерно в сторону действия силы Р?

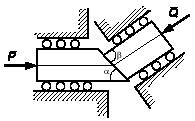
Задача 106

Однородный цилиндр помещен на наклонную плоскость, составляющую угол α с горизонтом так, что его образующие составляют угол β с горизонтальной линией, проведенной на плоскости. Определить условия, при которых цилиндр будет в покое, если f - коэффициент трения скольжения, δ - коэффициент трения качения, r – радиус цилиндра.

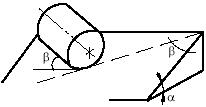
Задача 107

Груз веса Q привязан к неподвижной опоре тросом, составляющим с горизонтом угол β и помещен на призму веса G, наклонная грань которой составляет угол α с горизонтом. Определить минимальную силу Р, приводящую систему в движение, если угол трения груза о призму и призмы о плоскость равен φ.

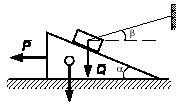
Задача 108

Из круга вырезали сектор с центральным углом α, а из окружности - дугу с таким же центральным углом. Получившиеся тела подвесили на нитях, как указано для первого тела на рисунке. Определить углы φ и φ₁, образуемые радиусами элементов круга и окружности с вертикалью при равновесии тел.

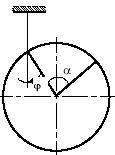
Задача 109

Храповое устройство позволяет двигаться направляющей 1 только влево. Считая, что коэффициент трения скольжения между шариком 2 и корпусом 3 значительно больше коэффициента трения скольжения f между шариком и направляющей, определить, при каком угле α храповое устройство работоспособно.

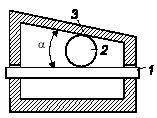
Задача 110

В стержневой системе АВ = АС, ВD = 2АВ, сила Т приложена к ползуну С, который может двигаться вдоль стержня ВD. Пренебрегая трением и весом стержней определить, при каком соотношении между силами Т и F система остается в равновесном положении, показанном на рисунке.

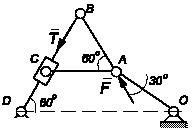
Задача 111

Круглое бревно весом 2Q и радиусом r касается вертикальной стены и удерживается в горизонтальном положении двумя одинаковыми балками АВ длиной l и горизонтальными тросами ВD. При каком угле α натяжение тросов будет наименьшим? Найти также наи-меньшее натяжение тросов. Весом балок и трением пренебречь; в точке А - шарнир.

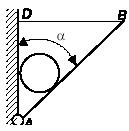
Задача 112

На трех однородных соприкасающихся друг с другом шарах одного радиуса лежит сверху такой же четвертый шар. Какими должны быть коэффициенты трения скольжения между двумя шарами и между шаром и горизонтальной опорной плоскостью, чтобы система была в равновесии?

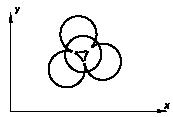
Задача 113

В стержневой системе, расположенной в вертикальной плоскости, АO1 = O1O2, стержни 1 и 2 однородны и имеют веса P1 и P2 соответственно. Определить силу натяжения пружины, если в положении равновесия системы, изображенном на рисунке, угол О1АВ = α , АBO2 = 90°, точки А, О1 и О2 лежат на одной прямой.

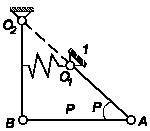
Задача 114

К тетраэдру ОAВС приложены пары сил с моментами М1, M2, M3, M4, расположенные в плоскостях YOZ, ZOX, XOY и АВС, соответственно. Определить момент результирующей пары сил, если М1 = 4 Нм; М2 = 3 Нм; М3 = 1 Нм; М4 = 3 Нм; ОА = ОВ = ОС.

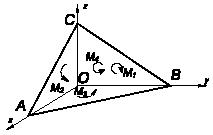
Задача 115

Однородный тяжелый стержень АВ длиной 2h расположен в вертикальной плоскости. Концом А он опирается на шероховатый пол, а промежуточной точкой С - на выступ высотой h. В точке А коэффициент трения f равен 0,6. Будет ли стержень находиться в равновесии? Трением в точке С пренебречь.

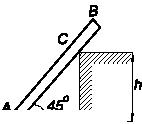
Задача 116

Цилиндр веса Q лежит на двух опорах С и D, расположенных симметрично относительно вертикали, проходящей через центр цилиндра. Коэффициент трения между цилиндром и опорами равен f. При какой величине тангенциальной силы Т цилиндр начнет вращаться? Напишите арифметический оператор присваивания, реализующий зависимость Т от Q, f, α (алгоритмический язык - по выбору).

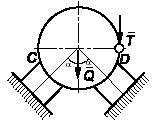
Задача 117

Однородный стержень АВ длины 2l опирается на полуокружность радиуса R. Определить, пренебрегая трением, угол φ в положении равновесия стержня.

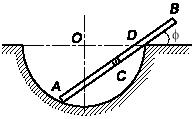
Задача 118

Стержень АС шарнирно закреплен на опоре в точке А и касается полудиска радиуса R и веса Q в точке В. Коэффициент трения скольжения между полудиском и опорной горизонтальной плоскостью f = 0,5. Какую вертикальную силу Р надо приложить к стержню в точке С, чтобы сдвинуть вправо полудиск, если АС = 2АВ = 2R ? Весом стержня и трением в контактной точке В пренебречь.

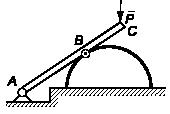
Задача 119

Однородный тонкий стержень АВ длиной l и весом Q шарнирно укреплен в точке А и опирается на вертикальную стену другим концом В. Вертикальная стена находится на расстоянии a от шарнира А. В момент возможного возникновения движения стержня определить значение угла α, который образует с вертикальной плоскостью YOZ плоскость ОАВ. Коэффициент трения между концом B стержня и стеной равен f. Трением в шарнире пренебречь.

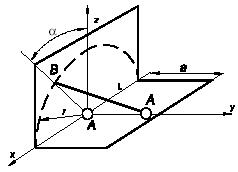
Задача 120

Однородный стержень АВ шарнирно укреплен в точке А и опирается в точке В о неподвижную тележку. Коэффициент трения в точке В равен 0,3, а сила давления стержня на тележку равна N. Сдвинется ли тележка влево, если приложить к ней горизонтальную силу, равную 0,25N ?

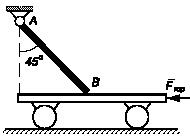
Задача 121

Однородный прямоугольный брус размерами a×a×2a, имеющий возможность вращаться вокруг оси О1О2, удерживается в равновесии нитью МК. Ось О1О2 проходит через вершину D и среднюю точку C ребра AВ, точка К лежит на продолжении прямой МЕ, ребро ЕА вертикально. Определить натяжение нити МК, если вес бруса Р. Трением в опорах пренебречь.

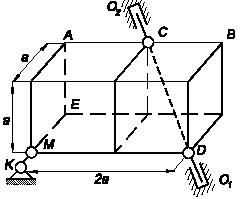
Задача 122

Какому условию должен удовлетворять размер h самотормозящего механизма, чтобы приложенная к узлу С сила Р не могла вызвать скольжения ползунов А и В по вертикальным направляющим? Коэффициент трения f = 0,2; расстояние между направляющими 2 м.

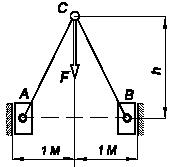
Задача 123

На горизонтальной гладкой поверхности стоит прямой полый цилиндр радиуса а. Внутри цилиндра находятся два шара весами P1 и Р2 и радиусами r₁ и r₂ соответственно. Нижний шар лежит на горизонтальной плоскости. Определить наименьший вес цилиндра, при котором шары его не опрокинут. Толщиной стенок цилиндра и трением пренебречь.

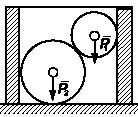
Задача 124

Определись наименьшее значение угла . наклона кривошипа к горизонту, при котором шатунно-кривошипный механизм ОАВ будет находиться в равновесии. Кривошип ОА, шатун АВ и ползун В имеют одинаковый вес, равный Р. Шатун и кривошип считать однородными стержнями, трением в шарнирах пренебречь. Коэффициент трения между ползуном и горизонтальной поверхностью f, ОА=В =a.

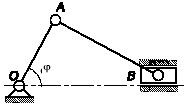
Задача 125

Шесть одинаковых однородных стержней веса Р, связанных шарнирно своими концами, образуют правильный шестиугольник, расположенный в вертикальной плоскости. Нижний стержень закреплен в горизонтальном положении. Какую направленную вертикально вверх силу нужно приложить к середине верхнего горизонтального стержня, чтобы система находилась в равновесии?

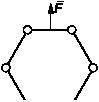
Задача 126

На горизонтальной плоскости стоит абсолютно гладкий цилиндр диаметра а и веса Р. В него опускают однородную палочку АВ длины 2l и веса Q, которая занимает положение равновесия под углом φ к горизонту. Найти угол φ и наименьший вес Q₀ палочки, при котором она в состоянии опрокинуть цилиндр, а также реакции в точках А и С в начальный момент опрокидывания. Указать соотношение между а и l, при котором возможно равновесие палочки. Толщиной стенок цилиндра пренебречь.

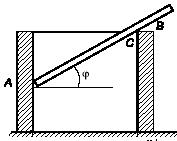
Задача 127

Тело весом Р покоится на шероховатой наклонной плоскости с углом наклона α. Коэффициент трения тела о плоскость равен f. Какому условию подчиняются величины α и f ? К телу прикладывают силу Q, лежащую в наклонной плоскости и направленную под углом β к линии наибольшего ската. При каком минимальном значении силы Q равновесие нарушится?

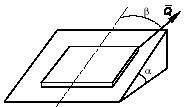
Задача 128

Определить условия, которым должны удовлетворять сила Р, приложенная к жесткому рычагу 1, момент пары М, приложенный к твердому кольцу 2 радиуса R, и коэффициенты сцепления (трения покоя) f_A и f_B в точках А и В, для того, чтобы кольцо вращалось вокруг неподвижной оси О. Трением в точке С, весом кольца и рычага пренебречь.

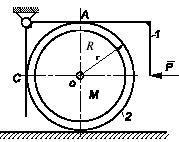
Задача 129

Однородная балка АВ весом Р, опирающаяся концом А на горизонтальную шероховатую поверхность, удерживается в горизонтальном положении нитью, образующей с ней угол 60° и переброшенной через блок. К концу нити подвешен груз D весом Q. Определить вес Q, при котором балка в указанном горизонтальном положении останется в равновесии, если коэффициент трения на опоре равен f.

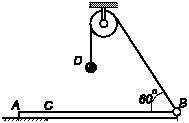
Задача 130

Однородная балка АВ весом Р, прикрепленная к полу шарниром А, опирается концом В на гладкую вертикальную стену, а промежуточной точкой С на гладкий стержень DС, заделанный в стену перпендикулярно к ее плоскости. Балка с плоскостью пола и ее горизонтальная проекция с плоскостью стены составляет равные углы по 45°. Определить реакцию шарнира А и реакции опор в точках B и С, если АВ = 4ВС.

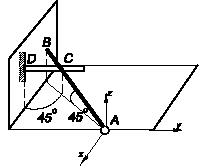
Задача 131

К концам двух невесомых стержней, подвешенных на шарнире О, прикреплены цилиндры 1 и 2 весом G каждый. Третий цилиндр весом Q опирается на два первые так, что вся система находится в равновесии. Найти зависимость между углами α и β.

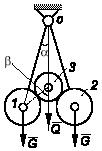
Задача 132

Над круглым отверстием в полу радиусом r положена тонкая круглая пластинка весом G и радиусом R; к ее краю приложена сила Q так, что пластинка может поворачиваться около прямой ВС. При каком расстоянии х сила Q будет минимальной?

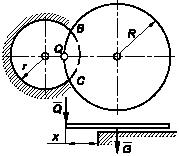
Задача 133

Какую силу Т надо приложить к нити, перекинутой через неподвижный блок, чтобы удержать в равновесии груз весом Q, закрепленный на другом ее конце? Коэффициент трения (нити о блок) f, α и R даны.

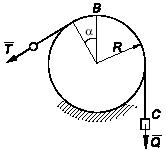
Задача 134

Раскатится ли система восьми одинаковых цилиндрических труб. Трение не учитывать. Определить реакции опор, действующие на трубу с номером 1.

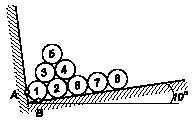
Задача 135

На наклонной плоскости с углом наклона α к горизонту лежит однородный диск весом Р и радиусом R. На диск намотана нить. К свободному концу нити, перекинутой через неподвижный, блок, подвешен груз весом Q. При каком значении Q диск будет равномерно скользить по плоскости, совершая одновременно качение без скольжения по бортику АВ? Коэффициент трения скольжения равен f, трение качения и трение на блоке не учитывать.

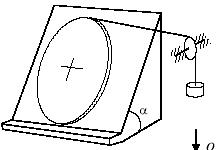
Задача 136

На горизонтальной прямоугольной платформе АBED в некоторой точке O стороны АD шарнирно прикреплен точкой обода однородный диск весом P и радиусом R. Платформу последовательно поворачивают в указанных на рисунке направлениях на угол α = 60° вокруг стороны АВ, затем на угол β = 30° вокруг стороны ВЕ. Первоначально точка О и центр диска С лежали на прямой, параллельной стороне АВ. 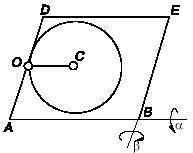Определить минимальные значения коэффициентов трения f1 и f2, при которых диск будет оставаться в равновесии после первого и второго поворотов платформы. Давление диска на опору равномерно распределено по площади.

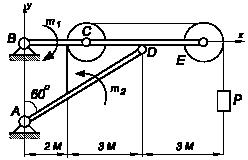
Задача 137

Два стержня BE и АD шарнирно соединены между собой и с опорами. В точках С и E стержня ВЕ шарнирно укреплены два одинаковых блока, через которые перекинута нить, закрепленная в точке К на стержне АD и несущая на свободном конце груз весом P. Методом возможных перемещений определить составляющие реакции шарниров y_A, x_D; Р = 20 Н; m₁ = m₂ = 120 Нм. Массой стержней, блоков и нити пренебречь, трение не учитывать.

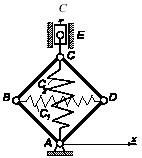
Задача 138

Четыре однородных стержня массой m и длиной l каждый с помощью шарниров образуют квадрат ABCD, противоположные вершины которого соединены пружинами жесткостью С1 и C2; длины пружин в недеформированном состоянии одинаковы. К вершине С квадрата с помощью невесомого стержня СЕ прикреплен ползун массой М, который может скользить в вертикальных направляющих. Пренебрегая трением, найти деформации пружин при равновесии.

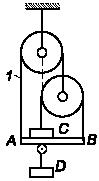
Задача 139

Два груза С и D веса Р каждый с помощью невесомых блоков одинакового радиуса, веревок и балки АВ приведены в состояние равновесия, причем балка горизонтальна. Определить усилие в ветви 1 веревки, если все ветви вертикальны, а ось блока с неподвижным центром и точка подвеса груза D лежат на одной вертикали.

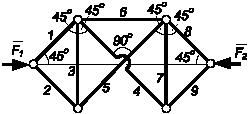
Задача 140

Определить усилие в стержне 6 стержневой конструкции, нагруженной одинаковыми по модулю силами Fi, которые направлены по одной прямой.

Задача 141

Однородный сплошной диск радиуса R и веса Р лежит на шероховатой горизонтальной плоскости. Какой по модулю момент M способен вызвать вращение диска вокруг оси OZ, перпендикулярной плоскости диска и проходящей через центр O, если давление диска на опорную плоскость распределено равномерно, а коэффициент трения скольжения о плоскость равен f ?

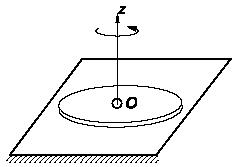
Задача 142

На шероховатой горизонтальной плоскости лежит полушар веса Q и радиуса r. В точке А на него действует горизонтальная сила Р. Найти угол α в предельном состоянии равновесия шара, если P=1/8Q. Под каким углом β надо приложить в точке А минимальную силу Р, чтобы она обеспечила предельное состояние равновесия при некотором угле α_min ? Найти Рmin и α_min.

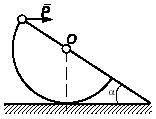
Задача 143

Два однородных полудиска O1A и O2B радиусов R и r соединены шарнирно однородным стержнем АВ. Веса дисков - Р, Q, вес стержня p. Система расположена в вертикальной плоскости, полудиски опираются о горизонтальный гладкий пол. Определить углы α и β при равновесии системы.

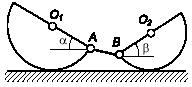
Задача 144

Круглое кольцо радиуса R посредством трех нитей одинаковой длины, прикрепленных к кольцу в равноотстоящих друг от друга точках, подвешено к неподвижной точке О. На образовавшийся таким образом конус надето меньшее кольцо радиуса r равного с первым веса. Кольцо это при равновесии системы делит нити пополам. Найти отношение расстояний колец от точки О.

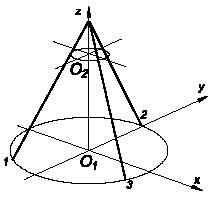
Задача 145

Круглая невесомая пластинка покоится в горизонтальном положении, опираясь центром на острие О. Разместить по окружности пластинки, не нарушая равновесия, грузы Р1 = 1,5 кН, Р2 = 1 кН, P3 = 2 кН в точках А, В и С, то есть найти углы α и β.

Задача 146

На горизонтальной гладкой опоре положен круглый цилиндр весом 2Q и радиусом r, разрезанный вертикальной плоскостью, проходящей через его ось. Чтобы части цилиндра не распадались, на середине его длины на него накинута нить, несущая на концах грузы весом Р каждый. Участки нити, непосредственно сходящие с цилиндра, образуют с горизонтом равные углы α. Определить наименьшую величину Р, при которой части цилиндра будут в покое. Найти также силу взаимодействия частей цилиндра и реакцию опоры при минимальном весе грузов.

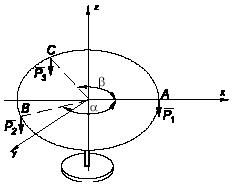
Задача 147

Шарнирный трехкратный параллелограмм находится под действием горизонтальных сил F и Q. Сила F задана. Определить величину силы Q, которая обеспечивает равновесие параллелограмма.

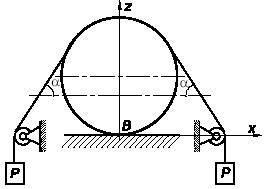
Задача 148

Для крепления прямоугольной плиты АВСD можно использовать любые из семи заданных шарнирных стержней. Указать все возможные комбинации стержней, обеспечивающие жесткое и статически определенное крепление плиты при любом ее нагружении.

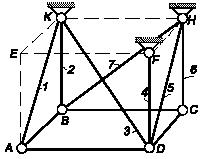
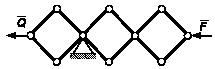
Задача 149

Из цилиндрической трубы радиуса r двумя взаимно перпендикулярными сечениями вырезан патрубок. На его внутреннюю поверхность действует равномерное давление Р. Определить величину и линию действия равнодействующей R.

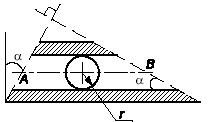
Задача 150

При каком условии автомобильное колесо радиуса R сможет медленно переехать через свободно лежащий на дороге цилиндр радиуса r ? Коэффициент трения цилиндра с колесом и дорогой f. Весом цилиндра пренебречь.

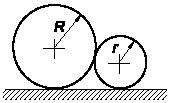
Задача 151

На какой высоте h следует приложить горизонтальную силу Р, чтобы каток, вес которого 10Р, равномерно скользил по горизонтальной поверхности без качения? Обозначить: f - коэффициент трения скольжения; δ - коэффициент трения качения.

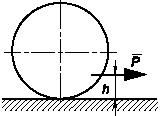
Задача 152

Раскатятся ли трубы на горизонтальном полу, если коэффициент трения скольжения между поверхностями труб f = 0,2? Трубы и пол считать абсолютно твердыми. При каком минимальном количестве труб нижнего ряда система не будет раскатываться? Зависит ли результат от количества труб, если учитывать трение качения?

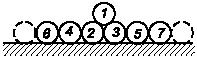
Задача 153

Конструкция состоит из трех однородных стержней одинакового веса Р, соединенных шарнирно в точке А, и невесомых ползунов В и С, связанных нерастяжимой нитью. Конструкция расположена в вертикальной плоскости. Трение в направляющих отсутствует. Углы между стержнями указаны на чертеже. Определить силы, действующие на каждый стержень в точке А.

Задача 154

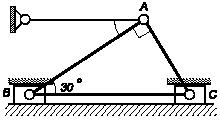
К треугольному ключу с сечением в виде прямоугольного треугольника с катетами АВ = а и ВС = b приложена пара сил с моментом М. Определить давления, производимые вершинами А, В и С на грани гнезда замка. Трением пренебречь. Зазор между ключом и гнездом считать малым.

Задача 155

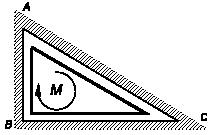
Однородный тонкий стержень длиной AB = l и весом P опирается в точке B на шероховатую поверхность с коэффициентом трения f <1, а в точке А на гладкую горизонтальную поверхность. В точке А к стержню прикреплена пружина жесткостью с, второй конец которой закреплен в точке D. Пружина недеформирована, когда стержень вертикален. Определить, при каких значениях угла α стержень будет находиться в равновесии, если P = 2cl.

Задача 156

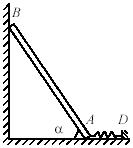
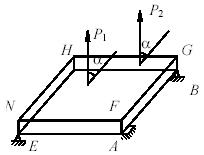
Прямоугольная однородная плита весом Q соединена с неподвижной опорой цилиндрическим шарниром А и сферическим шарниром В. Плита удерживается в горизонтальном положении острием Е, упирающимся в гладкую поверхность нижней грани плиты. К верхней грани плиты FGHN приложены две параллельные силы, равные Р и лежащие в плоскости этой грани. Линии действия сил образуют острый угол α со стороной NH, а центр тяжести плиты находится от них на равных расстояниях. Определить реакции опор, если известно, что AF=AB/5=AE/10.

Задача 157

Тонкая проволока, изогнутая в виде полуокружности, свободно висит на уголке, опираясь на него в точке М0. Определить: 1) при каких значениях коэффициента трения f возможно равновесие полуокружности, если точку контакта перенести в положение М, определяемое углом φ; 2) при каком угле φ минимальное значение коэффициента трения, обеспечивающее равновесие, является наибольшим. Найти этот максимум.

Задача 158

Однородный горизонтально расположенный квадрат ADBE весом P с диагоналями AB = DE = 2l прикреплен в точке А к неподвижной опоре сферическим шарниром. Квадрат уравновешен некоторой дополнительной системой активных сил, о которой известно: 1) линия действия равнодействующей этой системы проходит через точку В; 2) если к этой системе добавить вес квадрата, то при приведении новой системы сил к точке D ее главный момент равен Pl/2. Определить реакцию шарнира А, пренебрегая толщиной квадрата.

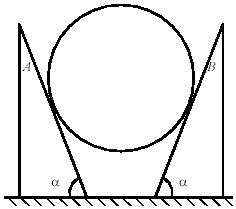
Задача 159

Две однородные треугольные призмы одинаковых размеров, сделанные из разных материалов, находятся на неподвижном основании, ребра их параллельны, и призмы удерживают в равновесии невесомый полый цилиндр, в который медленно наливают жидкость. Веса призм А и В соответственно равны P1 = 1 кН, P2 = 2 кН. Коэффициент трения между призмой A и цилиндром, а также неподвижной поверхностью f1 =0,2, для призмы В соответственно f2 = 0,15. Угол при основании призмы α = 60⁰. Определить какая из призм начнет скольжение первой, а также силу трения между другой призмой и горизонтальной поверхностью в этот момент, если положение цилиндра обеспечивает неопрокидывание призм.

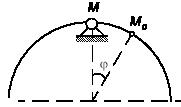
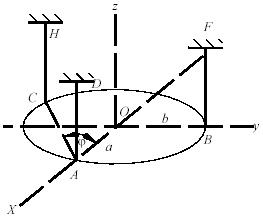
Задача 160

Однородная пластина весом Р в виде эллипса с полуосями a и b удерживается в горизонтальном положении тремя вертикальными нитями AD, BF, CH. Точки А, В и С лежат на пересечении эллипса соответственно с осями x, y и линией, проходящей через точку А и составляющей угол с осью x. Определить силу натяжения нитей, если tgφ=b/2a.

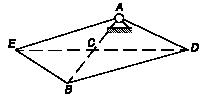
Задача 161

Однородный диск весом P и радиусом r находится в вертикальной плоскости. В точке B он касается неподвижной вертикальной стенки с коэффициентом трения f=. Невесомая нить намотана на диск и образует со стенкой угол α = 60°. К диску жестко прикреплен однородный стержень BD длиной 8r, расположенный горизонтально. На конец стержня действует вертикальная сила F = 2P. При каком значении веса стержня конструкция будет находиться в равновесии? Какой вес стержня обеспечивает равновесие при любом коэффициенте трения?

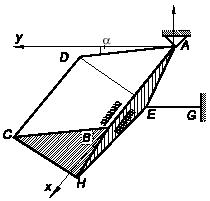
Задача 162

Невесомый симметричный треугольный короб ABCDEH длиной AB = CD = 4l со сторонами AE = DE = l и углом AED = 2π удерживается в равновесии сферическим и цилиндрическим шарнирами в точках А и В соответственно и невесомым стержнем EG. Ось шарниров А и В горизонтальна, а стержень EG расположен горизонтально в перпендикулярной ей плоскости. В короб наливается максимально возможное количество жидкости с массовой плотностью ρ. Определить величину реакции в шарнире А, если край короба AD составляет угол φ= 15° с горизонтом.

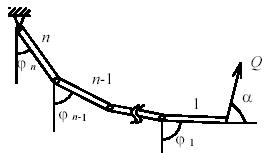
Задача 163

Система, состоящая из n одинаковых однородных стержней веса Р каждый, подвешена в вертикальной плоскости. Один конец этой системы шарнирно закреплен, а на второй действует сила Q, образующая угол α с горизонтом. (Р >Qsinα). Определить углы, которые образуют стержни с вертикалью в положении равновесия. Трением в шарнирах пренебречь.

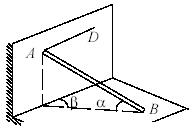
Задача 164

Тяжелый однородный стержень АВ одним концом А опирается на гладкую вертикальную стену, а другим концом В - на шероховатый горизонтальный пол. Конец А стержня удерживается горизонтальной нитью АD. Указать область значений для углов α и β, при которых стержень АВ будет находиться в покое в указанном на рисунке положении, если коэффициент трения скольжения между концом В стержня и полом равен f.

Задача 165

Гибкая однородная лента расположена внутри полого шероховатого цилиндра, ось которого горизонтальна. Лента образует дугу окружности с центральным углом 2α . Каково наиболее значение угла δ с вертикалью, при котором лента не соскальзывает, если коэффициент трения скольжения равен f?

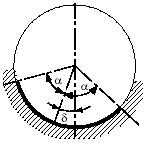
Задача 166

Два однородных стержня: ОА длиной l, весом Р и АС длиной 2l, весом 2Р, соединены шарниром А. Стержень ОА укреплен шарнирно, а стержень АС опирается на острие В. Определить, при каком угле φ система находится в равновесии в вертикальной плоскости, если расстояние ОВ = l (отрезок ОВ - горизонтальный).

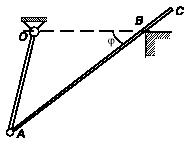
Задача 167

Одинаковые однородные стержни АВ и ВС длиной l соединены цилиндрическим шарниром, на оси которого укреплен невесомый ползун В. Стержни опираются в точках А и С на вертикальные гладкие стенки, расположенные на расстоянии а друг от друга (а < l). Ползун может скользить по шероховатому горизонтальному полу с коэффициентом трения f. При каком соотношении между а и l эта система будет находиться в равновесии в любом положении ползуна на плоскости?

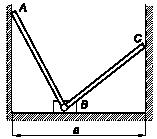
Задача 168

Два однородных стержня ОА длиной а, весом Р и АС длиной b, весом Q соединены шарниром А и находятся в вертикальной плоскости. Стержень ОА укреплен шарнирно, а стержень АС проходит через гладкую муфту В. Определить уравновешивающий момент М, удерживающий стержень ОА в горизонтальном положении под углом φ к стержню АС.

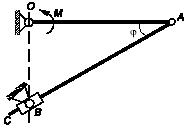
Задача 169

Рукоятка катка, шарнирно соединенная с его осью, опирается своим концом А на вертикальную гладкую стенку. Вес рукоятки равен Р, ее длина l, вес катка также равен Р, его радиус r. В точке В к катку приложена горизонтальная сила Q= 2Р. При каком угле α возможно равновесие системы, если коэффициент трения скольжения между катком и горизонтальной плоскостью равен f, а коэффициент трения качения равен δ.

Задача 170

Тонкий однородный стержень длиной 2r опирается на шероховатый диск радиуса r и удерживается в равновесии невесомой нитью длины r. Определить координаты точки С прикрепления нити, если угол наклона стержня с горизонталью равен φ и нить составляет с вертикалью также угол φ. Трением в шарнире О пренебречь.

Задача 171

Два одинаковых тонких однородных стержня АВ и ВС жестко скреплены в точке В под прямым углом. Стержень АВ расположен на шероховатой горизонтальной плоскости xAy с коэффициентом трения f, его крепление в точке А допускает поворот вокруг оси стержня АВ и перемещение в положительном направлении оси z. Стержень ВС в точке С опирается на вертикальную гладкую стену xAz. При каком значении f предельное значение угла φ при равновесии составляет 30°? Считать, что равнодействующие сил трения и нормальных реакций шероховатой плоскости приложены в одной точке, вертикальной составляющей реакции опоры A пренебречь.

Задача 172

Три одинаковых однородных диска радиуса R расположены в вертикальной плоскости, как указано на рисунке. Коэффициент трения между дисками, а также опорной поверхностью и дисками одинаков и равен f (f < 1). Определить максимальное расстояние между центрами нижних дисков и область допустимых значений коэффициента трения при равновесии системы.

Задача 173

Однородный прямоугольник с основанием a, высотой b и весом Q лежит на шероховатой горизонтальной плоскости с коэффициентом трения f. Каким условиям удовлетворяет величина силы Р, для которой прямоугольник находится в равновесии при любом значении угла α (0≤α≤π/2) ? Сила Р расположена в плоскости прямоугольника.

Задача 174

Дана система n материальных точек с массами m_k и координатами x_k, y_k, z_k, k = 1 … n. На каждую точку действует сила притяжения к некоторому центру Q: , где f - одно и то же для всех точек. Определить координаты точки Q, если известно, что система находится в равновесии.

Задача 175

Балка АВ весом 2P имеет шарнирную опору в точке А не закрепленную, а установленную на шероховатую плоскость. Коэффициент трения между плоскостью и опорой равен f. Шарнирно-подвижная опора В расположена на наклонной плоскости, образующей угол 45° с горизонтом. Определить точку приложения силы Р (абсциссу x) при которой нарушается равновесие, а также чему должны равняться f и x для того, чтобы в предельном положении равновесия балки вертикальные составляющие реакции опор А и В были бы одинаковы?

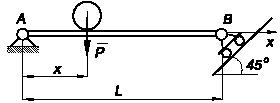
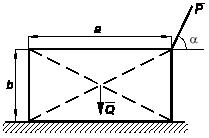
Задача 176

Картина АВ подвешена к вертикальной стене с помощью нити, прикрепленной к гвоздю в стене (О) и к картине в точке D. Определить длину нити OD и расстояние DA, для которых в положении равновесия сила трения обращается в нуль при любом значении угла α. Длина АВ = 2l.

Задача 177

Два однородных цилиндра массой m каждый положены на внутреннюю поверхность полого цилиндра. Они удерживают третий цилиндр массы М. Определить зависимость между углами α и β в положении равновесия.

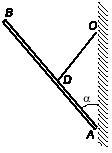
Задача 178

Стороны ромба ABCD, подвешенного в точке А, сделаны из тяжелых однородных стержней, соединенных шарнирно. Середины сторон BC и CD соединены невесомым стержнем-распоркой, которая фиксирует ромб. Зная вес Р ромба и длины его диагоналей АС=а и BD=b, определить усилие в распорке.

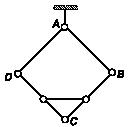
Задача 179

В кривошипно-шатунном механизме шатун выполнен в виде прямоугольного треугольника АВС (с горизонтальным катетом АС в данном положении), при этом ОА = АВ = r. Зная моменты пар сил М и m = M приложенных к кривошипу и шатуну, определить силу F, направленную вдоль АС и уравновешивающую механизм.

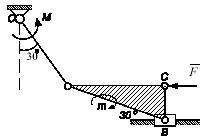
Задача 180

Треугольная пирамида SABC с равными ребрами и весом P расположена так, что ее основание АВС горизонтально, а вершины В и С закреплены с помощью неподвижных шарниров. В центре тяжести каждой боковой грани приложены силы, равные по модулю Р и направленные перпендикулярно к граням во внутрь пирамиды. Какую надо приложить в вершине S силу F, параллельную вектору АВ, чтобы пирамида находилась в данном положении в равновесии? Трение в шарнирах не учитывать.

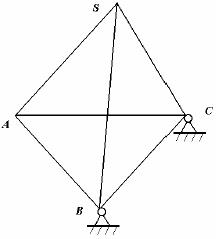
Задача 181

Механизм находится в равновесии под действием моментов М1, М2, М3, М4 и сил F, Q. Сила F приложена в середине отрезка CD перпендикулярно к нему, а сила Q приложена в середине DE параллельно CK; BD = DC = BC = a; CK = CN. Выразить силу Q через другие силовые факторы. Трение в шарнирах не учитывать.

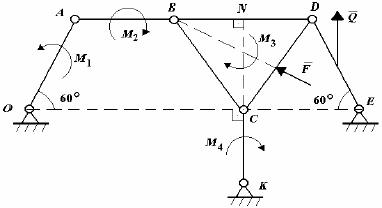
Задача 182

На гладкой наклонной плоскости с углом наклона α находятся два груза 1 и 2 друг на друге, коэффициент трения скольжения между ними равен f. Грузы соединены нитью, перекинутой через неподвижный блок. Вес верхнего тела Р2. Найти вес Р1 нижнего тела при равновесии системы.

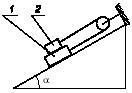
Задача 183

Две однородные балки АС и BD с весами Р1 и Р2 соответственно соединены шарниром С и невесомым стержнем ЕК с шарнирами на концах, при этом АС = l, BD = 1,5l, AE =EC = CK = KB и ∠ACB = 60°. Система находится в вертикальной плоскости и опирается в точках А и В на шероховатую горизонтальную плоскость с коэффициентом трения скольжения f. Какую горизонтальную силу Q надо приложить в точке D, чтобы система начала опрокидываться вокруг точки А, а опора А оставалась неподвижной? Найти также усилие S в стержне ЕК в момент начала опрокидывания системы.

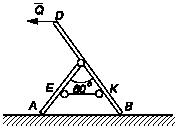
Задача 184

Две прямоугольные однородные плиты Р = 4 кН каждая соединены так, что могут вращаться вокруг неподвижной оси АВ независимо друг от друга, при этом в точке А - неподвижный пространственный шарнир, в точке В - подшипник. Плиты находятся в равновесии с помощью невесомых стержней CD и KL с шарнирами на концах. Плита 1 расположена в плоскости хОz, а плита 2 составляет с ней угол 30°. На плиту 2 действует сила F = 2 кН, приложенная в точке Е и направленная параллельно оси Оу, и вектор-момент m некоторой пары, направленной по ON и численно равный m = a кНм, а - в метрах. OA = OB = AN = BE = AD = OK = OC = a (м), KL - в плоскости уОz и KL⊥OL, OL∥AN. Определить величину и характер (растяжение-сжатие) усилий в стержнях CD и KL.

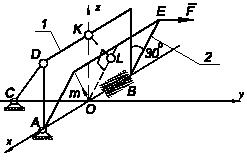
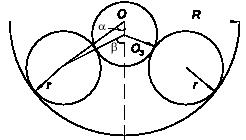
Задача 185

Три одинаковые трубы радиуса r находятся в равновесии в неподвижно закрепленной трубе радиуса R, располагаясь в два ряда. Все трубы малого радиуса касаются друг друга, при этом трубы нижнего ряда касаются также трубы большего радиуса. Найти наибольшее значение R, при котором равновесие системы еще возможно.

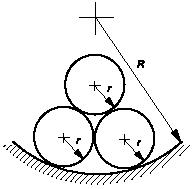
Задача 186

Плоский механизм находится в горизонтальной плоскости в равновесии под действием силы F и системы пар сил с моментами M₁, M₂, M₃, M₄. Углы указаны на рисунке, размеры звеньев O₁A=l, O₂B=2l, CD=1,5l. Выразить момент M₄ через остальные данные.

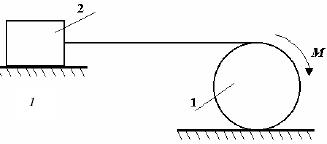
Задача 187

На однородный каток 1 радиуса R и веса Q, связанный с телом 2 нерастяжимой нитью, действует момент М. Коэффициент трения качения равен δ, коэффициент трения скольжения для тела 2 равен f. Каким должен быть наибольший вес P тела 2, чтобы он начал скользить и чему должен при этом быть равен коэффициент трения скольжения для тела 1?

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00