Примеры решения задач

где . Для определения N составим уравнение в проекции на ось B_y. Так как , получим , откуда . Следовательно, ; кроме того, и уравнение (8) примет вид

(9)

Разделив обе части равенства на т, вычислим ; 16/m=8 и подставим эти значения в (9). Тогда получим

(10)

Умножая обе части уравнения (10) на dt и интегрируя, найдем

Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t=0. Тогда при t=0 , где дается равенством (7). Подставляя эти величины в (11), получим

(11)

При найденном значении С₂уравнение (11) дает

(12)

Умножая здесь обе части, на dt и снова интегрируя, найдем

(13)

Так как при t=0 х=0, то С₃=0 и окончательно искомый закон движения груза будет

, где х - в метрах, t - в секундах. (14)

Пример Д1-3. Имея в точке А скорость _A, тело движется по горизонтальному участку АВ длиной l в течение с. Коэффициент трения скольжения тела по плоскости равен f. Со скоростью _B тело в точке В покидает плоскость и попадает в точку С со скоростью _c , находясь в воздухе Т с. При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать.

Дано: схема механизма (рис.Д1-3), ; ; ; .

Найти: , .

Решение. Рассмотрим движение тела на участке АВ. Принимая тело за материальную точку, покажем (рис. Д1-3) действующие на него силы: вес , нормальную реакцию и силу трения скольжения .

Составим дифференциальное уравнение движения тела на участке АВ:

; ,

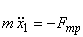Сила трения

где .

Таким образом,

;

или

Интегрируя дифференциальное уравнение дважды, получаем:

(1)

Для определения постоянных интегрирования С₁ и С₂ воспользуемся начальными условиями задачи:

при .

Рис. Д1-3

Составим уравнения, полученные при интегрировании формулы (1), для :

, .

Найдем постоянные интегрирования:

Тогда уравнения (1) примут вид:

(2)

Для момента t , когда тело покидает участок АВ,

то есть

откуда

;

т. е. .

Рассмотрим движение тела от точки В до точки С.

Показав силу тяжести , действующую на тело, составим дифференциальные уравнения его движения:

Начальные условия задачи: при t = 0

Интегрируем дифференциальные уравнения дважды:

(3)

Напишем полученные уравнения (3) для t = 0

Отсюда найдём, что

Получим следующие уравнения проекций скорости тела: из уравнений (3) и уравнения движения:

Найдём уравнение траектории тела, исключив параметр t из уравнений движения. Определив t из первого уравнения и подставив его значение во второе, получаем уравнение параболы:

В момент падения y=h, x=d.

Определяя d из уравнения траектории, найдем

Используя уравнение движения , найдём время движения тела от точки В до точки С, учитывая, что

Скорость тела при падении найдём через проекции скорости на оси координат

по формуле

Для момента падения t = T = 2 c.

или

Пример Д2. В приборе для измерения ускорений движущихся тел (рис. Д2) груз М массы m укреплен на пружине c коэффициентом жесткости c. Ось пружины совпадает с направлением движения аппарата. Аппарат движется по закону (неподвижная ось z направлена по вертикали вверх). Начальное удлинение пружины равно , а начальная скорость груза по отношению к аппарату – (направлена вертикально вниз).

Дано: m =0,2 кг, c = 100 Н/м, =0,01 м, =0,5 м/с.

Определить: х=f(t) – закон движения груза по отношению к аппарату.

Указания. Задача - охватывает одновременно относительное движение и колебания материальной точки.

Сначала нужно составить дифференциальное уравнение относительного движения (по отношению к лифту) рассматриваемого в задаче груза, для чего присоединить к действующим силам переносную силу инерции. Затем прикрепленные к грузу пружины (по условиям задачи их будет две) заменить эквивалентной пружиной с коэффициентом жесткости , произведя соответствующий расчет.

а) Если пружины соединены друг с другом последовательно (как пружины с жесткостями и на рис. Д2.0), то при равновесии под действием некоторой силы , приложенной к свободному концу пружины, усилия в любом поперечном сечении пружин одинаковы и равны Q. Удлинения пружин , , удлинение эквивалентной пружины и . Отсюда

б) Если груз прикреплен к двум параллельным пружинам (как к пружинам с жесткостями и на рис. Д2.1) или находится между двумя пружинами, то при равновесии под действием некоторой силы каждая из пружин и эквивалентная пружина имели бы одно и то же удлинение . Тогда для двух пружин , а для эквивалентной пружины – , отсюда .

После того, как уравнение будет составлено (это будет линейное дифференциальное уравнение 2-го порядка), его следует проинтегрировать, учтя начальные условия.

Рис. Д2

Решение.

Пусть груз прикреплен к концу эквивалентной пружины с жесткостью с и начальным удлинением (рис. Д2). В ускоренно движущейся системе отсчета, жестко связанной с аппаратом, на груз действуют сила тяжести , сила упругости и переносная сила инерции . Пусть начало 0 оси 0Х подвижной системы координат совпадает с концом недеформированной пружины, а ось Х направлена в сторону удлинения пружины. Уравнение относительного движения имеет вид

в векторной форме:

в проекции на ось х:

. (1)

Далее находим , , где – удлинение пружины, .

Учитывая, что оси z и x противоположно направлены, получим:

и .

Подставляя все найденные выражения проекций сил в уравнение (1), получим:

. (2)

Введем обозначения , b=2g=20 м/c².

Уравнение (2) теперь может быть записано в виде:

. (3)

Для нахождения закона движения груза необходимо проинтегрировать уравнение (3). Это уравнение является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Его решение находим в виде , где есть решение соответствующего однородного уравнения ,

. (4)

Величины и в уравнении (4) – неопределенные постоянные. Величина есть частное решение уравнения (3). Ищем его в виде , где А – постоянная величина. Подставляя это выражение в уравнение (3), получим или

Таким образом, общим решением уравнения (3) является выражение:

. (5)

Найдем величины и из начальных условий. Так как при t=0 , то из уравнения (5) получим:

или .

продифференцировав (5) один раз по t, получим

. (6)

Поскольку при t=0 , то из (6) получим , или .

Подставляя найденные выражения для и в уравнение (5), получим:

Подставим значения величин v₀, k, l₀, b и k².

Х = (0,022 sin(22,36t) – 0,03 cos (22,36t) +0,04) м.

Это уравнение и определяет искомый закон движения груза, т.е. закон совершаемых им колебаний.

Общие теоремы динамики

Пример Д3. Шарик, принимаемый за материальную точку, движется из положения А внутри трубки, ось которой расположена в вертикальной плоскости и пройдя путь h₀, отделяется от пружины. Найти скорость шарика в положениях В и С и давление шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь.

Дано: схема механизма (рис.Д3, б), 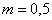кг, ; , ; , , , , .

Найти: , ,, .

Решение. Для определения и применим теорему об изменении кинетической энергии материальной точки. Движение шарика на участке АС и АВ траектории происходит под действием силы тяжести G, силы трения (силы трения на криволинейных участках не учитываем) и силы сжатия пружины (рис. Д3, а):

Откуда, учитывая, что 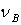= 0, получим

Для определения скорости применим теорему об изменении количества движения материальной точки

Так как , , то

Откуда получим

Определим скорость шарика в точке С. Движение на DC происходит только под действием силы тяжести (по условию), работа силы тяжести меньше нуля, т.к. точка поднимается.

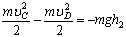где

Откуда получим

Определим давление шарика на стенку канала в положении С (рис. Д3-1).

В соответствии с принципом Даламбера для материальной точки геометрическая сумма сил, приложенных к точке, и силы инерции этой точки равна нулю:

Силу инерции материальной точки можно разложить на нормальную и касательную составляющие:

Сумма проекций сил и на ось x должна быть равна нулю:

Отсюда

Искомое давление шарика на стенку трубки по числовому значению равно найденной реакции и направлено в противоположную сторону.

Пример Д4. Механическая система состоит из грузов массы =5 кг и массы =12 кг и из прямоугольной вертикальной плиты массы =25 кг, движущейся вдоль горизонтальных направляющих (рис. Д4). В момент времени , когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобу, представляющему собой окружность радиуса R=1 м, по законам и , где t – в с, и – в рад.

Определить: – закон движения плиты и – закон изменения со временем полной нормальной реакции направляющих.

Указания. Задача - на применение теоремы о движении центра масс. При этом для определения составить уравнение в проекции на горизонтальную ось х, а для определения N - на вертикальную ось у.

Рис. Д4

Решение.

Механическая система выбрана так, что наперед неизвестные силы, т.е. силы упругости, с которыми каждый из грузов взаимодействует с плитой, являются внутренними. Поэтому при решении данной задачи применима теорема о движении центра масс.

Рассмотрим систему в произвольном положении (рис. Д4). Изобразим все внешние силы, действующие на систему: силы тяжести и реакцию направляющих . Проведем координатные оси ОXY так, чтобы оси Х и Y проходили через точку , где находился центр масс плиты в момент времени .

1. Для определения запишем уравнение, выражающее теорему о движении центра масс данной системы:

(1)

где – масса системы.

Проектируя обе части равенства (1) на координатную ось х, получим:

(2)

т.к. все внешние силы вертикальны.

Из уравнения (2) следует, что или .

Поскольку в начальный момент времени скорость , а следовательно, и проекция скорости были равны нулю, то и в любой момент времени 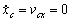, отсюда

, (3)

т.е. центр масс системы не перемещается вдоль оси ОХ.

Будем находить величину по формуле:

В произвольный момент времени х₁= х₃+ Rcos, х₂= х₃- Rsin.

В начальный момент времени (при t=t₀=0) х₁=Rcos, х₂= - Rsin2, х₃=0.

В соответствии с уравнением (3) координаты центра масс системы в начальный и произвольный момент времени равны:

Ответ: х= м, где t – в секундах.

2. Для определения N=f(t) запишем уравнение (1) в проекции на ось у:

. (4)

Учитывая, что P₁=m₁g, P₂=m₂g, P₃=m₃g, перепишем уравнение (4) в виде:

. (5)

Зависимость величины от времени определяет зависимость от времени величины N.

В соответствии с определением центра масс механической системы можем написать:

, (6)

Продифференцируем уравнение (6) два раза по времени:

С учетом найденного значения определим из уравнения (5) искомую зависимость N=f(t).

Ответ: N = 420–49,35sin(pt)-37,70sin(t²+2) -8,44t²cos(t²+2), где t – в секундах, N – в ньютонах.

Пример Д5. Механическая система состоит из прямоугольной вертикальной плиты 1 массы m₁, движущейся вдоль горизонтальных направляющих, и груза D массы m₂ (рис. Д5). В момент времени t₀= 0, когда скорость плиты , груз под действием внутренних сил начинает двигаться по желобу, представляющему собой окружность радиуса R, по закону .

Дано: m₁=12 кг, m₂=8 кг, =1,0 м/с, R=0,5 м, рад (t – в секундах).

Определить – закон изменения скорости плиты.

Указания. Задача – на применение теоремы об изменении количества движения системы. При решении составить уравнение, выражающее теорему, в проекции на горизонтальную ось.

Рис. Д5

Решение.

Рассмотрим систему, состоящую из плиты 1 и груза D, и определим внешние силы, действующие на нее. На груз D действует сила тяжести , на плиту действует сила тяжести и нормальная реакция направляющих . Применим к данной системе теорему об изменении количества движения в проекции на ось x, проведенную вдоль направляющих:

, . (1)

Здесь – проекция количества движения системы на ось . Поскольку силы все вертикальны, то из (1) получим

или . (2)

Таким образом, в условиях данной задачи выполняется закон сохранения количества движения системы в проекции на ось . Используя равенство (2), составим равенство начального (при ) и конечного (при произвольном t) количества движения системы:

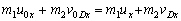; . (3)

В уравнении (3) буквой v обозначена скорость груза; и – конечные, а и – начальные значения проекций скоростей на ось .

Выразим величины, входящие в уравнение (3), через время и заданные величины:

Абсолютную скорость груза представим в виде суммы переносной скорости и относительной скорости :

В проекции на ось

Переносная скорость равна скорости поступательного движения плиты. Следовательно, , . Вектор относительной скорости направлен перпендикулярно радиусу СD вращения груза и по модулю равен

Поскольку

и , (4)

то в начальный момент времени положение груза определяется углом 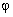=0 и =0. Отсюда =0.

С учетом найденного, .

В начальной фазе движения, когда время увеличивается от начального значения , и . Рассматривая груз D в произвольном положении в начальной фазе движения (груз D на рис. Д5) найдем выражение для проекции вектора на ось :

или

Подставим найденные выражения в уравнение (3)

Выражая и подставляя числовые данные задачи, получим закон изменения скорости плиты:

м/с.

Пример Д6. Однородная горизонтальная платформа (круглая радиуса R), имеющая массу , и стержень AB жестко скреплены в точке D, основании радиуса платформы CD, так, что стержень AB находится в плоскости платформы под прямым углом к радиусу CD. Платформа вращается с угловой скоростью вокруг вертикальной оси z, отстоящей от центра масс C платформы на расстоянии OC=0,5R (рис. Д6а). В момент времени на платформу начинает действовать пара сил с моментом M, направленным противоположно ; одновременно кольцо K массы , находящееся на стержне AB в точке D, начинает двигаться по стержню (под действием внутренних сил) по закону s = DK=F(t).

Дано: =10 кг , =1 кг, R =1 м , = 2 с^-1, s = 0,5 t ² (s – в метрах, t – в секундах), М = kt², где k=4 Нм/с².

Определить: – закон изменения угловой скорости платформы.

Указания. Задача – на применение теоремы об изменении кинетического момента системы. При применении теоремы к системе, состоящей из платформы и груза, кинетический момент К_z системы относительно оси z определяется как сумма моментов платформы и груза. При этом следует учесть, что абсолютная скорость груза складывается из относительной и переносной скоростей, т.е. . Поэтому и количество движения этого груза 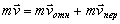. Тогда можно воспользоваться теоремой Вариньона (статика), согласно которой ; эти моменты вычисляются так же, как моменты сил.

При решении задачи полезно изобразить на вспомогательном чертеже вид платформы сверху (с конца оси z).

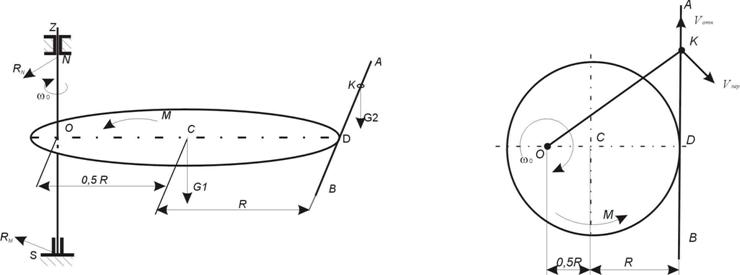
а) б)

Рис. Д6

Решение.

Рассмотрим механическую систему, состоящую из платформы и кольца K (рис. Д6а). На систему действуют внешние силы: сила тяжести платформы , сила тяжести кольца , силы реакции подшипников 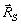и , а также пара сил с моментом M. Запишем теорему об изменении кинетического момента системы относительно оси z:

. (1)

Так как силы и параллельны оси z , а силы и пересекают ось z , то их моменты относительно оси z равны нулю. Будем считать положительным направление моментов против хода часовой стрелки, тогда .

Перепишем теперь уравнение (1) в виде:

Интегрируя, получим

. (2)

Для рассматриваемой механической системы

, (3)

где – кинетические моменты платформы и кольца соответственно.

Поскольку платформа совершает вращательное движение, то справедливо

, (4)

где – момент инерции платформы относительно оси z. Используя формулу Гюйгенса и формулу для момента инерции круглого диска относительно центральной оси, для величины получим:

Подставляя полученный результат в выражение (4), получим:

. (5)

Для нахождения кинетического момента рассмотрим рис. Д6б, на котором движение кольца K представлено в виде суммы двух движений. Относительное движение совершается со скоростью , переносное – со скоростью . Так как кольцо К движется по закону s=DK=0,5t², то . Направление вектора определяется знаком . В данных условиях задачи > 0. При < 0 направление на рис. Д6б было бы противоположным. Затем, учитывая направление , определяем направление вектора ( OK); численно .

По теореме Вариньона:

. (6)

Из рис. Д6б OD=1,5R ; OK² = OD² + s ² = 2,25R² + 0,25t⁴.

С учетом полученного перепишем формулу (6) в виде:

(7)

Подставляя формулы (5) и (7) в формулу (3), получим с учетом данных задачи:

тогда уравнение (2) примет вид (учтем k = 4):

. (8)

Постоянную интегрирования определяем по начальным условиям: при t = 0 . Получим = 5,25, = 10,5 кгм²/с.

Подставляя найденное значение в уравнение (8), находим искомую зависимость от t.

Ответ: =(5,33t³ – 6t+ 42)/(21 – t⁴), где t – в секундах, – в с^-1.

Пример Д7-1. Механическая система (рис. Д7а) состоит из груза 1, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней R₃ и r₃ и радиусом инерции относительно оси вращения , блока 4 и сплошного однородного цилиндрического катка 5. Коэффициент трения груза 1 о плоскость равен f. Тела системы соединены нитями, намотанными на шкив 3 и каток 5. К центру блока 2 прикреплена пружина с коэффициентом жесткости с; ее начальная деформация равна нулю.

Система приходит в движение из состояния покоя под действием силы F=f(s), зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М сил сопротивления.

а) б)

Рис. Д7

Дано: m₁ = 10 кг, m₂ = 0 кг, m₃ = 3 кг, m₄ = 1 кг, m₅ = 5 кг, R₃= =0,3 м, r₃ = 0,1 м, = 0,2 м, f = 0,1, c = 300 Н/м, M = 0,5 Н·м, F = 70(3+s) Н, s₁ = 0,2 м.

Определить: в тот момент, когда s = s₁.

Указания. Задача – на применение теоремы об изменении кинетической энергии системы. При решении задачи следует учесть, что кинетическая энергия Т системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении Т для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение s₁, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.

Решение.

Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 4, 5 и невесомого тела 2, соединенных нитями. На систему действуют внешние силы: активные , G₁, G₃, G₄, G₅, реакции опор , сила натяжения нити , силы трения и момент М.

Применим к системе теорему об изменении кинетической энергии:

. (1)

Так как в начальный момент система находилась в покое, то Т₀ =0. Кинетическая энергия системы Т складывается из кинетических энергий всех тел системы:

Т = Т₁ + Т₃ + Т₄ + Т₅. (2)

Учитывая, что тело 1 движется поступательно, тело 5 плоскопараллельно, а тела 3 и 4 совершают вращательное движение, получим:

Т₁=; Т₃=;

Т₄=; Т₅=. (3)

Все входящие сюда скорости надо выразить через искомую .

Отметим сначала, что радиус блока 4 и радиус катка 5 связаны соотношением r₄ = 2r₅. Из геометрии схемы также следует равенство r₅ = r₃, и, следовательно, r₄ = 2r₃. Заметим также, что v_c₅ = v_A, где А – любая точка обода радиуса r₃ шкива 3, v₅ =v₁ =v_B, где v₅ – скорость точки обода катка 5, диаметрально противоположной мгновенному центру скоростей катка К₅, а В – любая точка обода блока 4. Тогда:

(4)

Найдем моменты инерции, входящие в (3).

; ; . (5)

Подставив все величины (4) и (5) в равенство (3), а затем, используя равенство (2), получим окончательно:

. (6)

Теперь найдем сумму работ всех внешних сил при перемещении, которое будет иметь система, когда груз 1 пройдет путь s₁.

Работы восьми сил равны нулю, так как реакция перпендикулярна перемещению груза, силы , 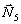и приложены в мгновенных центрах скоростей К₂ и К₅ и точки приложения сил неподвижны.

Введем обозначения: s_C₅ – перемещение центра катка 5, φ₃ –угловое перемещение шкива 3, – начальное и конечное удлинения пружины. Работы остальных сил равны:

А() =70(3+s)ds =35(6s₁ + s₁²),

A() = -s₁ = -fG₁s₁cos45⁰,

A(G₁) = G₁ s₁sin45⁰,

А() = -G₅ s_C₅ sin45⁰,

А(М) = -М ,

А() = ().

По условиям задачи =0. Тогда = s_E, где s_E – перемещение точки Е (конца пружины). Величины s_E, s_C₅ и надо выразить через заданное перемещение s₁; для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда, так как =, v_C₅ =0,5v₁ (см. равенства (4)), то и =, s_C₅=0,5s₁. Далее из рис. Д 7б видно, что v_Д = R₃, а так как точка К₂ является мгновенным центром скоростей для блока 2 (он как бы катится по участку нити K₂L), то v_Е=0,5v_Д=0,5R₃. Заменяя скорости перемещениями, получим s_E=0,5R₃=0,25(R₃/r₃)s₁. Используя найденные значения s_C₅, и , для суммы вычисленных работ получим:

(7)

Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что Т₀=0, получим равенство:

(8)

Из равенства (8), подставив в него числовые значения заданных величин, найдем искомую угловую скорость .

Ответ: =8,7 с^-1.

Пример Д7-2. Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на рисунках. Учитывая трение скольжения тела 1 и сопротивление качению тела 3, катящегося без скольжения, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s. Тело 2 и 3 считать сплошными однородными цилиндрами.

Дано: – масса груза 1, , , м, , , коэффициент трения скольжения , коэффициент трения качения см, 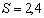м. На рис. Д7-2 показана механическая схема в начальном положении.

Найти: – скорость груза 1 в конечном положении.

Решение. Применим теорему об изменении кинетической энергии системы:

(1)

где Т₀ и Т – кинетическая энергия системы в начальном и конечном положениях; - сумма работ внешних сил, приложенных к системе, на перемещение системы из начального положения в конечное; - сумма работ внутренних сил системы на том же перемещении.

Для рассматриваемых систем, состоящих из абсолютно твёрдых тел, соединенных нерастяжимыми нитями и стержнями,

Так как в начальном положении система находится в покое, то Т₀= 0.

Следовательно, уравнение (1) принимает вид

(2)

Напишем кинематические соотношения между скоростями и перемещениями точек системы, т. е. уравнения связей, при этом перемещения и скорости тел выразим соответственно через скорости и перемещения груза 1.

Скорость центра масс катка 3 равна скорости груза 1:

. (3)

Угловая скорость катка 3, мгновенный центр скоростей которого находится в точке касания катка с плоскостью

. (4)

Угловая скорость блока 2 . (5)

Вычислим кинетическую энергию системы в конечном положении как алгебраическую сумму кинетических энергий тел 1, 2, 3:

. (6)

Кинетическая энергия груза 1, движущегося поступательно,

. (7)

Кинетическая энергия блока 2, вращающегося вокруг оси Ax:

. (8)

Момент инерции блока 2 относительно оси Ax:

. (9)

Подставляя выражения (5), (9) в формулу (8), получаем

Кинетическая энергия катка 3, совершающего плоское движение:

, (10)

где - момент инерции катка 3 относительно его продольной центральной оси :

. (11)

Подставляя (3), (4), (11) в формулу (10), получаем

. (12)

Кинетическая энергия всей системы:

. (13)

Найдём сумму работ всех внешних сил, приложенных к системе на заданном ее перемещении. Покажем внешние силы, приложенные к системе (рис. Д7-3):

для тела 1:

Работа сил тяжести G₁ :

(14)

Работа силы трения скольжения F_тр:

Так как

то . (15)

для катка 3:

Работа силы тяжести G₃будет отрицательной, т.к. начальное положение катка выше, чем конечное

. (16)

Работа силы сцепления катка , т.к. сила приложена в мгновенном центре скоростей катка.

Работа пары сил сопротивления качению катка 3:

где - момент пары сил сопротивления качению катка 3; - угол поворота катка 3.

Так как каток катится без скольжения, то угол его поворота

где S_C₃– перемещение центра тяжести С₃ катка 3.

В нашем случае перемещение центра масс катка 3 будет равно перемещению центра масс груза 1, т.е. S_C₃= S = 2,4 м.

Тогда работа пары сил сопротивления качению:

(17)

Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (14) – (17):

Согласно теореме (3.2), приравниваем значения и

откуда

Пример Д7-3. Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на рисунке. Учитывая трение скольжения тела 1 и сопротивление качению тела 3, катящегося без скольжения, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s. Тело 2 и 3 считать сплошными однородными цилиндрами.

Дано: – масса груза 1, , , м, , = 0,2 м, f = 0,12, = 0,25 см, s = 1,5 м

Найти: – скорость груза 1 в конечном положении.

Решение. Применим теорему об изменении кинетической энергии системы:

и (т.к. система состоит из абсолютно твердых тел и нерастяжимых нитей)

Кинетическая энергия системы равна:

, ,

Сумма работ внешних сил:

м/с.

Пример Д7-4. Механическая система (рис. Д2,а) состоит из сплошного однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней R₃ и r₃ и радиусом инерции относительно оси вращения , блока 4 и груза 5 (коэффициент трения груза о плоскость равен f). Тела системы соединены нитями, намотанными на шкив 3.

К центру Е блока 2 прикреплена пружина с коэффициентом жесткости с; ее начальная деформация равна нулю.

Система приходит в движение из состояния покоя под действием силы F=f(S), зависящей от перемещения S точки ее приложения. На шкив 3 при движении действует постоянный момент М сил сопротивления.

Дано: m₁ = 8 кг, m₂ = 0, m₃ = 4 кг, m₄ = 0, m₅ = 10 кг, R₃ = 0,3м, r₃=0,1м, =0,2м, f=0,1, c=240 H/м, М= 0,6 Нм, F=20(3+2s) H, s₁=0,2м.

Определить: в тот момент времени, когда S=S₁.

Рис. Д2

Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, соединенных нитями. Изобразим действующие на систему внешние силы: активные, реакции , натяжение нити , силы трения и момент М.

Для определения воспользуемся теоремой об изменении кинетической энергии:

. (1)

2. Определяем Т₀ и Т. Так как в начальный момент система находилась в покое, то Т₀=0. Величина Т равна сумме энергий всех тел системы:

(2)

Учитывая, что тело 1 движется плоскопараллельно, тело 5 - поступательно, а тело 3 вращается вокруг неподвижной оси, получим

(3)

Все входящие сюда скорости надо выразить через искомую . Для этого предварительно заметим, что , где A - любая точка обода радиуса r₃шкива 3 и что точка K₁ - мгновенный центр скоростей катка 1, радиус которого обозначим r₁. Тогда

; . (4)

Кроме того, входящие в (3) моменты инерции имеют значения

(5)

Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно

(6)

Теперь найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда центр катка 1 пройдет путь S₁. Введя обозначения: S₅ - перемещение груза 5 (S₅=S₁), - угол поворота шкива 3, и - начальное и конечное удлинения пружины, получим

;

Работы остальных сил равны нулю, так как точки К₁ и К₂, где приложены силы и - мгновенные центры скоростей; точки, где приложены силы и - неподвижны; а реакция перпендикулярна перемещению груза.

По условиям задачи, . Тогда , где - перемещение точки Е (конца пружины). Величины и надо выразить через заданное перемещение S₁; для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями:

Тогда так как (равенство уже отмечалось), то и

Далее, из рис. Д2,б видно, что , а так как точка К₂ является мгновенным центром скоростей для блока 2 (он как бы «катится» по участку нити K₂L), то ; следовательно, и .

При найденных значениях и для суммы вычисленных работ получим

(7)

Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что Т₀=0, придем к равенству

(8)

Из равенства (8), подставив в него числовые значения заданных величин, найдем искомую условную скорость

Ответ: =8,1c^-1.

Пример Д7-5. Механическая система (рис. Д3) состоит из обмотанных нитями блока 1 радиуса и ступенчатого шкива 2 (радиусы ступеней и , радиус инерции относительно оси вращения р₂), а также из грузов 3 а 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к блоку 1.

Дано:

Определить: ускорение груза 3, пренебрегая трением.

Рис. Д3

Указания. Задача Д3 – на применение к изучению движения системы общего уравнения динамики (принципа Даламбера – Лагранжа). Ход решения задачи такой же, как в задаче Д2, только предварительно надо присоединить к действующим на систему силам соответствующие силы инерции. Учесть при этом, что для однородного тела, вращающегося вокруг своей оси симметрии (шкива), система сил инерции приводится к паре с моментом , где - момент инерции тела относительно оси вращения, - угловое ускорение тела; направление противоположно направлению .

Решение.

1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на эту систему, - идеальные.

Для определения а₃ применим общее уравнение динамики:

(1)

где - сумма элементарных работ активных сил; - сумма элементарных работ сил инерции.

2. Изображаем на чертеже активные силы и пару сил с моментом М. Задавшись направлением ускорения а₃, изображаем на чертеже силы инерции и пару сил инерции с моментом , величины которых равны: