Главная
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ
7.1. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
,
,
.
Решение: Скорости точки:
,
,
Модуль скорости:
Ускорения точки:
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.2. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
,
,
.
Решение: Скорости точки:
,
,
Модуль скорости:
Ускорения точки:
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.3. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, 
.
Решение: Скорости точки:
,
,
Модуль скорости:
.
Ускорения точки:
,
,
Модуль полного ускорения:
.
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.4. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, 
.
Решение: Скорости точки:
,
,
Модуль скорости:
Ускорения точки:
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.5. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, 
.
Решение: Скорости точки по осям:
,
,
Модуль скорости:
Ускорения точки по осям:
,
,
Модуль ускорения:
.
Модуль касательного ускорения точки:
, а модуль нормального ускорения 
.
Нормальное ускорение и радиус кривизны траектории связаны
соотношением 
.
7.6. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: , , 
.
Решение: Скорости точки по осям:
,
,
Модуль скорости:
Ускорения точки по осям:
,
,
Модуль ускорения:
.
Модуль касательного ускорения точки:
,
а модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны
соотношением 
.
7.7. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, 
.
Решение: Скорости точки:
,
,
Модуль скорости:
Ускорения точки:
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.8. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, .
Решение: Скорости точки:
,
,
Модуль скорости:
.
Ускорения точки:
,
,
Модуль полного ускорения:
.
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.9. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, 
,
.
Решение: Скорости точки:
,
,
Модуль скорости:
.
Ускорения точки:
,
,
Модуль полного ускорения:
.
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.10. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, 
.
Решение: Скорости точки:
,
,
Модуль скорости:
Ускорения точки:
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.11. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, .
Решение: Скорости точки:
,
,
Модуль скорости:
Ускорения точки:
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.12. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: , 
, 
, .
Решение: Скорости точки:
,
,
Модуль скорости:
Ускорения точки:
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.13. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, .
Решение: Скорости точки:
,
,
Модуль скорости:
Ускорения точки:
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.14. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, 
.
Найти: 
, 
, 
.
Решение: Скорости точки по осям:
,
,
Модуль скорости:
,
Ускорения точки по осям:
,
,
Модуль ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.15. Определить касательное и нормальное ускорения, радиус кривизны траектории
точки для заданного момента времени.
Дано: 
, 
, .
Решение: Скорости точки:
,
,
Модуль скорости:
Ускорения точки:
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.16. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, .
Решение: Скорости точки:
,
,
Модуль скорости:
Ускорения точки:
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.17. Определить касательное и нормальное ускорения, радиус кривизны
траектории точки для заданного момента времени.
Дано: 
, 
, .
Решение: Скорости точки:
,
,
Модуль скорости:
Ускорения точки:
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.18. Дан закон движения точки по окружности радиусом r. Определить:
1) скорость и ускорение точки при 
и 
;
2) моменты остановки точки;
3) путь, пройденный точкой за 10секунд.
Дано: 
,
,
,
.
Найти: 
,
,
,
,
,
,
П.
Решение: 1. На траектории отметим точку О
– начало отсчета координаты s и укажем положительное направление отсчета этой координаты.
Отметим положение точки в заданные моменты времени: При 
:
;
При :
.
Проведем из этих точек естественные оси координат.
Определим проекцию скорости на касательную:
.
При :
;
При :
.
Векторы и совпадают со своими проекциями. Определим
проекции ускорения на естественнее оси координат:
;
,
Полное ускорение точки 
.
При :
,
и
.
При 
:
,
и
.
2. Чтобы найти время остановки надо найти время, когда скорость точки равна нулю:
,
получим 
и 
.
3. Поскольку за 10 секунд точка
сделала две остановки, пройденный ею путь за 10с можно найти как сумму пути,
пройденного от начала до первой остановки, от первой до второй остановки и от второй
до момента времени :
,
где:
;
;
;
.
Путь пройденный точкой за 10 секунд:
.
7.19. Определить скорость, касательное и нормальное ускорения, радиус
кривизны траектории точки для заданного момента времени.
Дано: 
, 
(1)
(x и y – в см, t и t1 – в с).
Найти: 1) вид траектории;
2) для t=t1 положение точки на траектории;
3) 
.
Решение: 1) Уравнение движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключаем время t из уравнений (1).
Возводя обе
части равенств в квадрат, а затем складывая равенства,
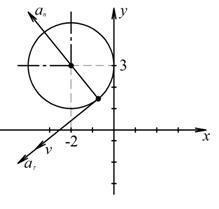
получаем 
, т.е. траекторией точки М является окружность радиуса 2, показанная на рис.1.
2) Определяем положение точки М в заданный момент времени t=1 с:
Вектор скорости точки
. (2)
Вектор ускорения
(3)
Здесь 
– орты осей 
и 
; 
– проекции скорости и
ускорения точки на оси координат.
Найдем их, дифференцируя по времени уравнения движения (1):
По найденным проекциям определяем модуль скорости:
,
(4)
,
,
и модуль ускорения точки:
,
(5)
Модуль касательного ускорения точки
,
(6)
или
; (7)
выражает проекцию
ускорения точки на направление ее скорости. Знак «+» при
означает, что движение
точки ускоренное, направление 
и 
совпадают; знак «–» –
что движение замедленное.
Вычисляем модуль касательного ускорения для заданного момента времени
Модуль нормального ускорения точки
.
(8)
Если радиус
кривизны траектории 
в рассматриваемой
точке неизвестен, то нормальное ускорение можно определить по формуле
.
(9)
При движении точки в плоскости формула (9) принимает вид
.
Модуль нормального ускорения можно определить и следующим образом:
.
(10)
Воспользуемся в нашем случае формулой (10)
Радиус кривизны траектории в рассматриваемой точке определим из выражения:
.
(11)
Тогда 
На рис. 1
показано положение точки М в заданный
момент времени. Вектор строим по составляющим
и 
, причем этот вектор должен по направлению совпадать с
касательной к траектории. Вектор 
строим по составляющим
и 
и
затем раскладываем на составляющие и 
. Совпадение величин 
и 
, найденных из чертежа, с их значениями, полученными аналитически,
служит контролем правильности решения.
7.20. Определить скорость, касательное и нормальное ускорения, радиус
кривизны траектории точки для заданного момента времени.
Дано: х =3t, у =4t2 –1
(x и y – в см, t и t1 – в с).
Найти: 1) вид траектории;
2) .
Указания. Задача - относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения. В задаче все искомые величины нужно определить только для момента времени t1 =1 с.
Решение:
1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t:
t = х/3,
у = 4(х/3)2 – 1.
Отсюда окончательно находим уравнение траектории точки (параболы, см. рисунок):
y = 4/9 х2 – 1.
2. Скорость точки найдем по ее проекциям на координатные оси:
Vx = dx/dt =3,
Vy =dy/dt =8t,
V =
и при t1 = 1 с,
V1х = 3 см/с,
V1у =8 см/с,
V1 =8,54 см/с. (1)
3. Аналогично найдем ускорение точки:
ах =dVx/dt =0,
аy =dVy/dt =8,
а =
и при t1 = 1 с
а1х=0; а1у =8 см/с2;
а1=8 см/с2. (2)
4. Касательное ускорение найдем, дифференцируя по времени равенство:
V2 =Vx2 + Vy2.
Получим: 2V dV/dt =2Vx dVx/dt +2Vy dVy/dt,
откуда:
. (3)
числовые значения всех величин, входящих в правую часть выражения (3), определены и даются равенствами (1) и (2).
Подставив в (3) эти числа, найдем сразу, что при t1 = 1 с
=7,49 см/с2.
5. Нормальное ускорение точки:
an =
.
Подставляя сюда найденные числовые значения a1 и a1τ, получим, что при t1= 1 с
a1n =2, 81 см/с2.
6. Радиус кривизны траектории ρ = V2/ an.
Подставляя сюда числовые значения V1 и a1n, найдем, что при t1 = 1 с
ρ1 =25,95 см.
Ответ: V1= 8,54
см/с, а1 =8 см/с2, =7,49 см/с2, a1n =2,81 см/с2, ρ1 =25,95 см.
7.21. Точка движется по дуге окружности радиуса R =1 м по закону 
(s – в метрах, t –
в секундах), где s = AM (см. рисунок).
Найти: скорость и ускорение точки в момент времени t1 =1 с.
Решение:
Определяем скорость точки:
V =ds/dt
=
.
При t1 =1 с получим 
= -1,26 м/с.
Ускорение находим по его касательной и нормальной составляющим:
,
an =V2/ρ = V2/R.
при t1 = 1 с получим, учтя, что R = 1 м
,
a1n =1,59 м/с2,
тогда ускорение точки при t1 =1 с будет:
=1,59 м/с2.
Изобразим на рисунке векторы 
, 
, учитывая знак V1 и считая положительным направление от А к М.
7.22. По заданным уравнениям движения точки М установить вид её
траектории и для момента времени t=t1(с) найти положение точки на траектории, её
скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны
траектории.
Дано: 
, 
, t1=1 сек (x и y – в см, t и t1 – в с).
Найти: 1) вид траектории;
2) 
.
Решение:
1) Найдём траекторию движения:
Для этого исключим параметр t.
Возведём во вторую степень, получившиеся уравнения, а затем сложим, таким образом, исключится t. Получим:
Это окружность с центром в точке
с координатами (-1;0) и радиусом 
2) Найдём положение точки на траектории в момент
времени t=t1:
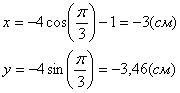
3) Определим скорость токи:
По оси Ox:
для момента времени t=t1:
По оси Oy:
для момента времени t=t1:
Для нахождения вектора полной скорости необходимо сложить 2 вектора:
Найдём модуль полной скорости:
для момента времени t1:
4) Определим ускорение точки:
По оси Ox:
для момента времени t1:
По оси Oy:
для момента времени t1:
Найдём полное ускорение:
Найдём модуль полного ускорения:
для момента времени t1:
Определим
касательное ускорение 
:
или, 
для момента времени t:
Определим нормальное ускорение an:
для момента времени t1:
5) Из
полученных результатов можно найти радиус кривизны траектории , в момент времени t1:
Действительно,
этот радиус совпадает с радиусом окружности (траектории).
7.23. Точка М движется согласно уравнений 
; 
; (x, y - в метрах, t -
в секундах). Определить уравнение траектории точки, для момента времени t =1с,
найти положение точки, а также скорость, полное, касательное, нормальное
ускорения точки и радиус кривизны траектории.
Решение:
1) Найдем уравнение траектории точки. Для определения уравнения
траектории исключим из уравнений движения время . Из первого уравнения движения точки найдем 
Из второго уравнения движения
найдем 
Возведя полученные значения ( правую и левую стороны уравнения ) в квадрат и складывая их находим:
.
Следовательно, траекторией точки является эллипс с центром в точке с координатами (3;1).
Вид траектории показан на рисунке.
2) Найдем положение точки в момент времени t=1с
; 
.
Положение точки М1 показано на рисунке.
3) Найдем скорость точки М
,
Где 
, или в момент времени t1=1c
, или в момент времени t1=1c
Следовательно
4) Найдём ускорение точки.
,
где 
, или 
,
, или 
Следовательно
5) Найдем касательное ускорение точки M,
6) Найдём нормальное ускорение точки M ,
7) Найдем радиус кривизны траектории точки М,
,
Направление векторов показано на рисунке.
Ответ: 
=7.85м/c;
= 4.93 м/c2; 
=0; 
= 4.93 м/c2; 
м
7.24. Пусть точка М движется в плоскости xOy в соответствии с
уравнениями 
. Для момента времени 
= 0,5 с найти
положение точки М на траектории, ее
скорость, полное, касательное и нормальное ускорения, а также радиус кривизны
траектории.
Решение: Заданный закон движения точки в координатной форме можно рассматривать как параметрические уравнения траектории точки. Исключим время t из уравнений движения и получим уравнение траектории точки в виде:
.
Таким образом, траекторией точки М является эллипс со смещенным центром, изображенный на рис. Отметим на траектории положение точки М1 (x1, y1) в момент времени t1 = 0,5 c
;
.
Вектор скорости точки представим в виде:
,
где 
– орты координатных
осей Оx и Оy; 
– проекции вектора
скорости точки на координатные оси, которые равны 1-м производным от
соответствующих координат по времени
В момент времени t1 = 0,5 c
Вектор скорости точки 
строим по двум взаимно
перпендикулярным проекциям 
и 
в соответствии с
выбранным масштабом
.
Полученный вектор должен быть направлен по касательной к траектории точки в сторону движения. Модуль скорости точки определим по уже найденным проекциям
Вектор ускорения точки представим в виде:
,
где – орты координатных
осей Оx и Оy; 
– проекции вектора скорости
точки на координатные оси, которые равны 1-м производным от проекций вектора
скорости или 2-м производным от соответствующих координат по времени:
В момент времени t1 = 0,5 c
Вектор ускорения точки 
строим по двум взаимно
перпендикулярным проекциям 
и 
в соответствии с
выбранным масштабом
.
Полученный вектор ускорения точки в общем случае должен отклоняться от вектора скорости в сторону вогнутости траектории, а при движении по эллипсовидной траектории – проходить через центр эллипса. Модуль ускорения точки определим по уже найденным проекциям
Вектор полного ускорения точки можно также представить в виде геометрической суммы его проекций на оси естественной системы отсчета
,
где 
и 
– единичные орты
касательной и главной нормали; 
и 
– соответственно
проекции вектора ускорения на касательную и главную нормаль. Касательную М1t
направляем по касательной к траектории в сторону движения точки движения, а
главную нормаль М1n – перпендикулярно касательной в
сторону вогнутости траектории. При вычислении касательного ускорения удобно
воспользоваться формулой, устанавливающей связь между координатным и
естественным способами задания движения точки
.
В момент времени t1 = 0,5 c
.
Значение касательного ускорения 
имеет отрицательный
знак, следовательно, в данный момент времени движение точки замедленное и
вектор касательного ускорения 
направлен в
противоположную сторону направлению вектора скорости точки .
Нормальное ускорение 
вычислим по формуле 
, если известен радиус кривизны траектории. Например, если
точка движется по окружности радиусом R,
то в любой точке траектории 
. Если же траекторией движения точки является прямая, то 
, следовательно, 
. В данном случае радиус кривизны траектории заранее не известен,
поэтому нормальное ускорение определяем по формуле:
.
В момент времени t1 = 0,5 c
.
Построим векторы и 
в соответствии с уже
выбранным масштабом, а затем сложим их геометрически. В результате получим тот
же вектор полного ускорения точки 
, который ранее уже был получен геометрической суммой
составляющих и . Этот факт служит контролем правильности решения.
Радиус кривизны траектории в рассматриваемой точке определим по формуле
.
В момент времени t1 = 0,5 c
.
Ответ: 
=8,82
см; 
=2,59
см; 
=4,44 см/c;
=2,22 см/c; 
=4,96 см/с; 
=6,97 см/с2; 
=3,49 см/с2; 
=7,79 см/с2;
=4,67 см/с2;
=6,23 см/с2;
=3,95 см (радиус кривизны траектории в точке 
).
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
