Главная
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ
10.1. Определить угловую скорость зубчатого колеса 2 и указать на
чертеже направление его вращения, если известна угловая скорость 
.
Радиусы зубчатых колес указаны на чертеже.
Дано: ,
.
Найти:
.
Решение: Линейная скорость обода первого колеса равна скорости обода четвертого, и равна:
,
Откуда угловая скорость колеса 4:
.
А линейная скорость обода третьего равна скорости обода второго и равна:
,
Откуда угловая скорость колеса 2:
10.2. Определить угловую скорость зубчатого колеса 2 и указать на
чертеже направление его вращения, если известна угловая скорость 
.
Радиусы зубчатых колес. указаны на чертеже.
Дано: ,
,
.
Найти: .
Решение: Линейная скорость обода колеса 1 равна скорости обода 3 и равна:
,
А линейная скорость обода третьего равна скорости обода второго и равна:
,
Откуда угловая скорость второго колеса:
.
10.3. Колесо 3 зубчатой передачи приводится во вращение посредством
ременной передачи, шкив 2 который жестко связан с колесом 3.
Определить угловую скорость зубчатого колеса 4, если угловая скорость
шкива 1 ременной передачи равна 
.
Дано: , 
, 
, 
, 
.
Найти: ω4.
Решение: Скорость ремня:
,
Откуда угловая скорость шкива 2:
.
Так как шкив 2 жестко связан с колесом 3, то их угловые скорости равны, и линейная скорость ободов колес 3 и 4 равны:
,
Откуда угловая скорость зубчатого колеса 4:
.
10.4. Колесо 3 зубчатой передачи приводится во вращение посредством
ременной передачи, шкив 2 который жестко связан с колесом 3.
Определить угловую скорость зубчатого
колеса 4, если угловая скорость шкива 1 ременной передачи равна .
Дано: , 
, 
, 
, 
.
Найти: ω4.
Решение: Скорость ремня:
,
Откуда угловая скорость шкива 2:
.
Так как шкив 2 жестко связан с колесом 3, то их угловые скорости равны, и линейные скорость ободов колес 3 и 4 равны:
,
Откуда угловая скорость колеса 4:
10.5. Колесо 3 зубчатой передачи приводится во вращение посредством
ременной передачи, шкив 2 который жестко связан с колесом 3.
Определить угловую скорость зубчатого колеса 4, если угловая скорость
шкива 1 ременной передачи равна .
Дано: , 
, 
, 
, 
.
Найти: ω4.
Решение: Скорость ремня:
,
Откуда угловая скорость шкива 2:
.
Так как шкив 2 жестко связан с колесом 3, то их угловые скорости равны, и линейные скорость ободов колес 3 и 4 равны:
,
Откуда угловая скорость колеса 4:
10.6. Колесо 3 зубчатой передачи приводится во вращение посредством
ременной передачи, шкив 2 который жестко связан с колесом 3.
Определить угловую скорость зубчатого колеса 4, если угловая скорость
шкива 1 ременной передачи равна 
.
Дано: 
, 
, 
, 
, 
.
Найти: 
.
Решение: Модуль линейной скорости ремня должен быть одинаков во всех его точках, поэтому:
.
Так как Шкив 2 жестко связан с колесом 3, то у них должна быть одинаковая угловая скорость:
.
Скорость точки стыка колес 3 и 4 – одинакова, поэтому:
.
10.7. Колесо 3 зубчатой передачи приводится во вращение посредством
ременной передачи, шкив 2 который жестко связан с колесом 3.
Определить угловую скорость зубчатого
колеса 4, если угловая скорость шкива 1 ременной передачи равна 
.
Дано: 
, 
, 
.
Найти: 
.
Решение: Линейная скорость ремня равна линейной скорости обода колеса 1 и линейной скорости обода шкива 2:
,
Откуда угловая скорость шкива 2, равная угловой скорости колеса 3, так как они жестко связаны:
.
Линейные скорости ободов колес 3 и 4 равны так как они соприкасаются:
,
Откуда угловая скорость колеса 4:
.
10.8. Механизм лебедки, состоящей из барабана Б и зубчатой передачи,
приводится в движение рукояткой ОА длинной 60см, жестко связанной с колесом 1.
Определить скорость подъема груза Р, если конец А рукоятки движется со
скоростью 
. Радиусы колес и барабана показаны на чертеже.
Дано: 
, 
, 
, 
.
Найти: 
.
Решение: Угловое ускорение рукоятки равно угловой скорости колеса 1:
.
Скорость точки стыка колес (1 и 2) и (2 и 3)– одинакова, поэтому:
.
Оно равно угловому ускорению барабана Б и скорость груза:
.
11.1. Стержень АВ длиной 50см перемещается в вертикальной плоскости
так, что его центр О движется по горизонтали по закону 
;
одновременно с этим стержень вращается вокруг оси О, перпендикулярной к
плоскости движения, с постоянной угловой скоростью 
.
Предполагая, что в начальный момент времени стержень АВ был вертикален,
определить скорости точек А и В в момент, когда он
повернется на угол 
.
Дано: ,
,
.
Найти: 
,
.
Решение: Момент времени, определяемый углом:
.
Скорость центра О, принимаемый за полюс:
.
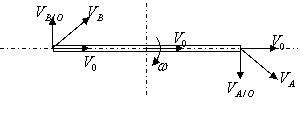Скорости
и 
направлены перпендикулярно стержню и
определяются как:
.
Так как 
и 
,
то скорости и определятся по теореме Пифагора из векторного
произведения 
и 
:
.
11.2. Стержень АВ длиной 50см перемещается в вертикальной плоскости
так, что его центр О движется по горизонтали по закону ; одновременно с этим стержень вращается вокруг оси О,
перпендикулярной к плоскости движения, с постоянной угловой скоростью .
Предполагая, что в начальный момент времени стержень АВ был вертикален,
определить скорости точек А и В в момент, когда он
повернется на угол .
Дано: , , 
.
Найти: , .
Решение: Момент времени, определяемый углом:
.
Скорость центра О, принимаемый за полюс:
.
Скорости и направлены
перпендикулярно стержню и определяются как:
.
Скорости и определятся по формуле:
и
.
В скалярном виде:
.
11.3. Стержень АВ длиной 50см падает в вертикальной плоскости так, что
его центр С движется по вертикали с ускорением 
. Одновременно в этой же плоскости стержень вращается с
постоянной угловой скоростью 
вокруг центра С. В
начальный момент стержень занимал вертикальное положение, скорость его центра С
равнялась нулю.
Определить скорости точек А и В в момент,
когда стержень повернулся на угол .
Дано: 
, , , 
.
Найти: , .
Решение: Момент времени определяемый углом :
.
Скорость центра С, принимаемый за полюс, в данный момент времени:
.
Скорости и 
направлены
перпендикулярно стержню и определяются как:
.
Скорости и определятся по
формуле:
и
.
В скалярном виде:
,
.
12.1. Стержень АВ длиной 60см скользит своими концами А и В по сторонам
угла.
Определить скорости точек В и С, а также угловую скорость стержня, если
скорость точки А равна 
.
Дано: 
, 
, 
,
, 
.
Найти: 
,
.
Решение: Показываем для заданного
положения стержня направление скоростей и .
Проектируя эти скорости на линию АВ, получим:
,
откуда скорость точки В:
.
Находим мгновенный центр
скоростей, находящийся в точке Р (находится на пресечении перпендикуляров к
скоростям и ).
Угловая скорость балки:
Скорость точки С:
.
12.2. Стержень АВ длиной 60см скользит своими концами А и В по сторонам
угла.
Определить скорости точек В и С, а также угловую скорость стержня, если
скорость точки А равна .
Дано: , , 
,
, 
.
Найти: ,
.
Решение: Показываем для заданного
положения стержня направление скоростей и .
Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке С (находящейся на пересечении перпендикуляра к
скоростям 
и ).
Из рисунка видно, что:
.
Угловая скорость балки вокруг мгновенного центра скоростей:
.
Скорость точки С:
.
12.3. Стержень АВ длиной 60см скользит своими концами А и В по сторонам
угла.
Определить скорости
точек В и С, а также угловую скорость стержня, если скорость точки А равна .
Дано: ,
, ,
,
.
Найти: ,
.
Решение: Показываем для заданного
положения стержня направление скоростей и .
Проектируя эти скорости на линию АВ, получим:
,
откуда скорость точки В:
.
Находим мгновенный центр
скоростей, находящийся в точке Р (находится на пресечении перпендикуляров к
скоростям и ).
Из рисунка видно, что:
и
.
Угловая скорость балки:
Скорость точки С:
.
12.4. Стержень АВ длиной 60см скользит своими концами А и В по сторонам
угла.
Определить скорости точек В и С, а также угловую скорость стержня, если
скорость точки А равна .
Дано: ,
, , , .
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P
(находится на перпендикуляре к скоростям и ).
Угловая скорость балки:
.
Скорость точки С:
.
12.5. Стержень АВ длиной 60см скользит своими концами А и В по сторонам
угла.
Определить скорости точек В и С, а также угловую скорость стержня, если
скорость точки А равна .
Дано: , , 
, .
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P
(находится на перпендикуляре к скоростям и ).
Угловая скорость балки:
.
Скорость точки С:
.
12.6. Стержень АВ длиной 60см скользит своими концами А и В по сторонам
угла.
Определить скорости
точек В и С, а также угловую скорость стержня, если скорость точки А равна .
Дано: , , 
.
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и .
Проектируя эти скорости на линию АВ, получим:
,
Откуда:
.
Находим мгновенный центр
скоростей (он находится на пересечении перпендикуляров к скоростям и ), находящийся в точке Р. Угловая скорость балки:
Скорость точки С:
,
Из рисунка видно, что
и тогда:
.
12.7. Стержень АВ длиной 60см скользит своими концами А и В по сторонам
угла.
Определить скорости точек В и С, а также угловую скорость стержня, если
скорость точки А равна .
Дано: , , .
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
,
Откуда скорость точки В:
.
Находим мгновенный центр
скоростей, находящийся в точке Р (находящийся на пересечении перпендикуляров к
скоростям и .
По теореме синусов:
.
По теореме косинусов:
.
Угловая скорость балки:
.
И тогда скорость точки С:
.
12.8. Стержень АВ длиной 60см скользит своими концами А и В по сторонам
угла.
Определить скорости точек В и С, а также угловую скорость стержня, если
скорость точки А равна .
Дано: , 
, 
, 
, .
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P
(находящийся на перпендикуляре к скоростям и ). Из рисунка видно, что:
.
.
Угловая скорость балки:
.
Скорость точки С:
.
12.9. Стержень АВ длиной 60см скользит своими концами А и В по сторонам
угла.
Определить скорости точек В и С, а также угловую скорость стержня, если
скорость точки А равна .
Дано: , , 
, 
, .
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P (находящийся на перпендикуляре к скоростям и ). Из рисунка видно, что:
.
.
Угловая скорость балки:
.
Скорость точки С:
.
12.10. Стержень АВ длиной 60см скользит своими концами А и В по
сторонам угла.
Определить скорости точек В и С, а также угловую скорость стержня, если
скорость точки А равна .
Дано: , , , 
, .
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр скоростей, находящийся в точке С. Угловая скорость балки:
.
Скорость точки С:
.
12.11. Стержень АВ длиной 60см скользит своими концами А и В по
сторонам угла.
Определить скорости точек В и С, а также угловую скорость стержня, если
скорость точки А равна .
Дано: , , 
, , .
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P
(находящийся на перпендикуляре к скоростям и ). Из рисунка видно, что:
.
.
Угловая скорость балки:
.
Скорость точки С:
.
12.12. Стержень АВ длиной 60см скользит концом А вдоль прямой, опираясь
промежуточной точкой С на неподвижную опору.
Определить угловую
скорость стержня, а также скорость точек В и С, если скорость точки А стержня
равна .
Дано: , , 
, 
.
Найти: , .
Решение: Показываем для заданного
положения стержня направление скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P (находящийся на перпендикуляре к скоростям и ). Из рисунка видно, что:
,
.
.
Угловая скорость балки:
.
Скорость точки В:
.
12.13. Стержень АВ длиной 60см скользит концом А вдоль прямой, опираясь
промежуточной точкой С на неподвижную опору.
Определить угловую скорость стержня, а также скорость точек В и С, если
скорость точки А стержня равна .
Дано: , , , 
.
Найти: , .
Решение: Показываем для заданного
положения стержня направление скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P (находящийся на перпендикуляре к скоростям и ). Из рисунка видно, что:
,
.
.
Угловая скорость балки:
.
Скорость точки В:
.
12.14. Стержень АВ длиной 60см скользит концом А вдоль прямой, опираясь
промежуточной точкой С на неподвижную опору.
Определить угловую скорость стержня, а также скорость точек В и С, если
скорость точки А стержня равна .
Дано: , , 
, 
.
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P
(находящийся на перпендикуляре к скоростям и ). Из рисунка видно, что:
,
.
Угловая скорость балки:
.
Скорость точки В:
.
12.15. Стержень АВ длиной 60см скользит своими концом А вдоль прямой,
опираясь промежуточной точкой С на неподвижную опору.
Определить угловую скорость стержня, а также
скорость точек В и С, если скорость точки А равна .
Дано: , , 
, 
.
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P
(точка пересечения перпендикуляров к скоростям и ).
Из треугольников можно выразить:
и
,
Угловая скорость балки:
.
И скорость точки В:
.
12.16. Стержень АВ длиной 60см скользит своими концом А вдоль прямой,
опираясь промежуточной точкой С на неподвижную опору. Определить угловую
скорость стержня, а также скорость точек В и С, если скорость точки А равна .
Дано: , , 
, 
.
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P (точка пересечения перпендикуляров к скоростям и ).
Из треугольников можно выразить 
и 
и угловая скорость
балки:
.
И скорость точки В:
.
12.17. Стержень АВ длиной 60см скользит своими концом А вдоль прямой,
опираясь промежуточной точкой С на неподвижную опору.
Определить угловую скорость стержня, а также скорость точек В и С, если
скорость точки А равна .
Дано: , , , 
.
Найти: , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P
(точка пересечения перпендикуляров к скоростям и ).
Из треугольников можно выразить:
и
,
.
и угловая скорость
балки:
.
И скорость точки В:
.
12.18. Стержень АВ длиной 60см скользит концом А вдоль прямой, опираясь
промежуточной точкой С на неподвижную опору.
Определить угловую скорость стержня, а также скорость точек В и С, если
скорость точки А стержня равна .
Дано: , , , 
.
Найти: , , 
.
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P
(находящийся на перпендикуляре к скоростям и ). Из рисунка видно, что:
,
.
Угловая скорость балки:
.
Скорость точки В:
.
12.19. Стержень АВ длиной 60см скользит концом А вдоль прямой, опираясь
промежуточной точкой С на неподвижную опору.
Определить угловую скорость стержня, а также скорость точек В и С, если
скорость точки А стержня равна .
Дано: 
, , 
, .
Найти: , , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P
(находящийся на перпендикуляре к скоростям и ). Из рисунка видно, что:
,
Угловая скорость балки:
.
Скорость точки В:
.
12.20. Стержень АВ длиной 60см скользит концом А вдоль прямой, опираясь
промежуточной точкой С на неподвижную опору.
Найти: угловую
скорость стержня, а также скорость точек В
и С, если скорость точки А стержня равна 10 см/с.
Дано: , 
см/с, 
, .
Найти: , , .
Решение: Показываем для заданного положения стержня направление
скоростей и . Проектируя эти скорости на линию АВ, получим:
.
Находим мгновенный центр
скоростей, находящийся в точке P (находящийся на перпендикуляре к скоростям и ). Из рисунка видно, что:
,
Угловая скорость балки:
.
Скорость точки В:
.
12.21. Колесо 1 (см. рис.)
вращается вокруг неподвижной оси по закону 
, рад и приводит в движение механизм подъёма груза 4.
Механизм состоит из двух ступенчатых колес 2 и 3, соединенных ременной
передачей и вращающихся вокруг неподвижных осей.
Найти: скорость и ускорение груза 4 в момент времени t = 3 с,
если R1 = 40 см, R2 = 15 см, R3 = 25 см, r2 = 10 см, r3 = 20 см.
Решение: Определим угловую скорость зубчатого колеса 
с-1. Точка контакта колес 1 и 2 является в данный
момент времени их общей и ее скорость 
, откуда 
. Далее, приравнивая скорости точек B и 
, принадлежащих в этот момент времени колесам 2, 3, получим
связь между угловыми скоростями этих колес 
, откуда 
. Подставляя выражение для угловой скорости 
и значения радиусов
колес, определим
.
Так как 
, вычислим скорости точки М
и груза 4 при t = 3 с
см/с.
Ускорение груза 4 равно вращательному ускорению точки М, т.е.
.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
