Примеры решения задач

Главная

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО СТАТИКЕ

Пример 1. Барабан лебедки (рис. 1, а) диаметром d_б = 0,14 м и приводится в равномерное вращение с помощью зубчатого колеса расчетным диаметром d = 0,25 м, на зуб которого действует расположенная в плоскости колеса сила F = 6 кН. Пренебрегая весом частей механизма, а также трением в подшипниках и на барабане, определить грузоподъемную силу лебедки.

Рис.1

Решение. Вал с насаженными на него деталями вращается равномерно, т.е. находится в равновесии, если сумма моментов действующих на детали сил относительно оси вращения равна нулю:

; ;

отсюда

G = 10 кH,

где d_б/2 - радиус барабана, являющийся плечом силы G относительно оси Z;

d/2 - радиус зубчатого колеса, являющийся плечом касательной составляющей Fсоs20° силы F. Нормальная же составляющая Fсоs70° пересекает ось Z и момента относительно оси не создает (плечо силы равно нулю).

При решении задач с пространственно расположенными силами целесообразно составлять дополнительный чертеж, спроецировав силы на плоскость, перпендикулярную оси вращения (рис. 1, б).

Это объясняется тем, что момент силы относительно оси равен моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Ответ: G=10 кН.

Пример 2. На валу установлен барабан, к которому подвешен груз весом G = 350 кH (рис. 1, а). Какой момент М нужно приложить к рукоятке, чтобы груз оставался в покое, если радиус барабана r = 240 мм? Силы тяжести вала и барабана не учитывать.

Рис.1

Решение. На вал действуют сила тяжести груза G, реакции опор R_A, R_B и пара сил с моментом М на рукоятке. Выберем систему координат, как показано на рис. 1, б, и составим уравнения равновесия вала:

; ,

откуда

Нм.

Если принять длину рукоятки h = 0,7 м, то сила на рукоятке F = M/h = 84/0,7 = 120 H.

Ответ: M=84 Нм.

Пример 3. На горизонтальный вал АВ насажены зубчатое колесо С радиуса 1 м и шестерня D радиуса 10 см. Другие размеры указаны на рисунке. К колесу С по направлению касательной приложена горизонтальная сила =100 Н, а к шестерне D, также по касательной, приложена вертикальная сила . Определить силу и реакции подшипников А и В в положении равновесия (рис. 1).

Рис.1

Решение. Отбрасывая связи вала (подшипники), прикладываем к валу их реакции, разложенные на составляющие R_AX, R_AZ, R_BX, R_BZ (см. рис. 1).

Составляем уравнения равновесия сил, произвольно расположенных в пространстве:

; (1)

; (2)

; (3)

; (4)

. (5)

Из уравнения (4) имеем, что

Н кН.

Подставляя значение = 1 кН в уравнение (3), получим:

кН.

Зная значение R_BZ из уравнения (2):

кН.

Из уравнения (5) следует, что

кН.

Тогда из уравнения (1):

кН.

Следует отметить, что уравнение дает тождество 0 = 0.

Полная реакция опоры А

кН.

Полная реакция опоры В

кН.

Ответ: кН; кН; кН.

Пример 4. Для горизонтального вала, несущего два зубчатых колеса с центрами О₁ и О₂и нагруженного, как показано на рис. 4.7, а, определить реакции опор А и В вала, если в точках С и D соответственно приложены силы: Н, Н, Н, Н. Радиусы зубчатых колес соответственно равны r₁ = 120 мм и r₂ = 80 мм. Вал по длине имеет размеры: l₁ = 60 мм, l₂ = 140 мм, l₃ = 100 мм.

Рис.1

Решение. Освобождая вал от связей (подшипников) в точках А и В, заменяем связи их реакциями. Выбираем пространственную систему координат с началом в точке А так, чтобы ось Х располагалась по оси вала, ось Y - параллельно силам и и ось Z - параллельно силам и . Принимая во внимание, что сил, действующих параллельно оси вала (оси Х), на схеме не имеется, в точках А и В будут приложены реакции связей, располагающиеся параллельно внешним силам, приложенным к валу в точках C и D, а именно: в точке А - R_AZ и R_AY, а в точке В - R_BZ и R_BY. В итоге на вал будет действовать пространственная система восьми произвольно расположенных сил: , , , - внешние силы и R_AZ, R_AY, R_BZ, R_BY - реакции связей (рис. 1, б).

Из условия равновесия данной системы сил определим неизвестные реакции связей в опорах А и В вала, составив шесть уравнений равновесия:

; ; ; ; ; .

Перед составлением уравнений равновесия заметим, что, например, силы , , R_AZ, R_AY, R_BZ, R_BY имеют моменты относительно оси Х, равные нулю, потому что эти силы пересекают ось Х непосредственно или своим продолжением (силы и ). Силы и , а также R_AZ и R_BZ не дают моментов относительно оси Z потому, что они параллельны этой оси, а сила R_AZ расположена на самой оси Z.

Аналогично этому моменты сил , , R_AY, R_BY относительно оси Y также обращаются в нуль. Уравнения равновесия системы сил принимают вид:

- силы системы проекций на ось Х не дают; (1)

(2)

(3)

- уравнение не имеет неизвестных; (4)

(5)

(6)

Для определения неизвестных реакций опор вала используем четыре уравнения равновесия

Из уравнения (5) находим

Н.

Из уравнения (3)

Н.

Из уравнения (6) находим

Н.

Из уравнения (2)

Н.

Полная реакция опоры А

Н.

Полная реакция опоры В

Н.

Ответ: Н; Н.

Пример 5. На рис. 1 изображен коленчатый вал двигателя. При вертикальном положении средней плоскости колена шатуна сила F, действующая на середину шейки вала, составляет 12 кН и направлена к плоскости, перпендикулярной к оси вала, под углом 15° к горизонтали. На оси вала в точке С закреплен маховик весом G = 12 кН. В точке Е укреплен шкив диаметром D = 80 см с ремнем, передающим момент на вал рабочей машины. Ветви ремня расположены в плоскости шкива и составляют с горизонталью угол, равный 30°. Отношение натяжения ведущей и ведомой ветвей ременной передачи F₁/F₂=2. Расстояние от оси вала до оси шейки колена r = 15 см. Расстояния вдоль оси вала показаны на рис. 1. Определить величины натяжения ветвей ремня F₁ и F₂ и реакции подшипников вала А и В при равномерном его вращении и заданном его положении. Весом шкива и вала пренебрегаем.

Рис.1

Решение. Приложенные к валу силы должны удовлетворять условиям их равновесия. Прикладываем к валу заданные внешние силы: вес маховика G, силу давления на шейку F и реакции ветвей ремня F₁ и F₂, направленные по касательной к окружности обода шкива. Отбрасывая мысленно связи, наложенные на вал в виде подшипников, заменяем их реакциями вала, разложенными на составляющие R_AY_, R_AZ_, R_BY, R_BZ (рис. 2).

Рис.2

Выбрав оси координат X, Y, Z, как показано на рис. 2, составляем уравнения равновесия системы сил, произвольно расположенных в пространстве.

Составим уравнения моментов сил относительно осей координат:

1. ; .

Так как = 2, то

откуда

кН;

кН.

При вычислении моментов сил , и относительно оси Y проецируем каждую из этих сил на плоскость, проходящую через точку приложения силы перпендикулярно оси Y.

Полученные проекции параллельны оси Z.

2. ;

откуда

кН.

Аналогично при составлении уравнения находим проекции сил , , на плоскости, перпендикулярные к оси Z. Эти проекции параллельны оси Y и соответственно имеют величины

3. ;

откуда

кН.

Составляем уравнения проекций сил на оси Y и Z; так как все действующие силы перпендикулярны к оси X, уравнение преобразуется в тождество 0 = 0.

4. ;

откуда

кН.

5. ;

откуда определяем

кН.

Полная реакция опоры А

кН.

Полная реакция опоры В

кН.

Ответ: кН; кН.

Пример 6. Для горизонтального вала, несущего зубчатое колесо с центром О, как показано на рис. 1, а, определить реакции опор А и В вала, если в точке С приложены силы: F_t = 1006 H, F_r = 382 H, F_a = 201 H. Диаметр зубчатого колеса d = 100 мм. Вал по длине имеет размеры: l₁ = 0,05 м, l₂ = 0,05 м.

Рис.1

Решение:

1. Составляем расчётную схему вала (рис. 1, б).

2. Составляем расчётную схему вала в горизонтальной плоскости (рис. 1, в), определяем реакции опор:

Н.

3. Составляем расчётную схему вала в вертикальной плоскости (рис. 1, г) и определяем реакции опор.

Н×м;

Н;

Н.

Проверка:

Полная реакция опоры А

Н.

Полная реакция опоры В

Н.

Ответ: Н; Н.

Пример 7. Вал со шкивом загружен в состоянии равновесия грузом F и силами F₁ и 0,5F₁ (F₁ = 200 H). Требуется определить реакции опор. Расположения шкивов и их диаметры заданы: а = 15 см, b = 25 cм, с = 40 см, D = 50 см, d = 20 см.

Прототипом примера является промежуточный вал зубчатых редукторов, применяемых в приводных станциях к сельскохозяйственным транспортёрам.

Решение. Решим пример аналитическим способом на основе системы уравнений равновесия пространственной системы сил:

Применим эти уравнения к определению опорных реакций R_AX, R_AY, R_AZ, R_BX, R_BY, R_BZ и уравновешивающей силы F вала, несущего на себе два зубчатых колеса (или шкива) различных диаметров (рис. 1). Выбор системы координат показан на рис. 1. За ось Х принимаем ось вала.

Уравнение моментов относительно оси вала

откуда

Н.

Рис.1

Уравнение моментов относительно горизонтальной координатной оси У

отсюда

Н.

Уравнение моментов относительно вертикальной оси координат Z

откуда

Н.

Для определения остальных неизвестных применим уравнения проекций сил на оси координат. Первое из них имеет вид

Чтобы определить каждую из неизвестных сил, необходимо принять во внимание, что подшипники валов в машинах устанавливаются обычно так, чтобы один из них, например А, допускал небольшое продольное смещение («люфт») и тем самым не оказывал сопротивления при давлении на него вдоль оси. В этом случае осевая реакция R_AX будет равна нулю, а R_BX = F_осевой = Н.

Второе уравнение проекций запишется следующим образом:

откуда

Н.

Третье уравнение

откуда

Н.

Полная реакция опоры А

Н.

Полная реакция опоры В

Н.

Ответ: Н; Н.

Пример 8. Квадратная однородная пластина ОАВС, сила тяжести которой равна G, удерживается в горизонтальном положении сферическим шарниром А и гибкой нерастяжимой нитью BD, составляющей с вертикалью угол (рис. 1, а). Найти реакции шарниров в точках О и А, натяжение нити, если .

а) б)

Рис.1

Решение. Внешние связи для пластины - шарниры в точках А, О и нить. Заменим их реакциями связей. Реакцию сферического шарнира представим в виде трех составляющих R_OX, R_OY, R_OZ. Реакцию цилиндрического шарнира представим в виде двух составляющих R_AX, R_AZ, а реакцию нити N направим вдоль линии BD (рис. 1, б).

Для составления уравнений равновесия силу N удобно разложить на две составляющие, одна из которых N₂ параллельна оси Z, другая N₁ расположена в плоскости XOY и направлена по диагонали пластины. При этом

Уравнения равновесия:

(1)

(2)

(3)

(4)

(5)

(6)

Из уравнения (6) системы

R_AX = 0.

Из уравнения (5)

N₂ = 0,5G, .

Далее из уравнения (4) найдем

Тогда из уравнений (1 - 3):

R_О_Z = 0,5G,

Полная реакция опоры O

Полная реакция опоры A

Ответ:

Пример 9. Тренога ABCD шарнирно опирается на горизонтальную плоскость (рис. 1, а) в точках A, B и C. В точке D тренога имеет блок. Через блок перекинут гибкий трос, один конец которого закреплен в точке Е стены, а к другому прикреплен груз F = 10 кH. Определить реакции стержней треноги.

Рис.1

Решение. 1. Пренебрегая размерами блока, считаем, что заданные силы и искомые реакции стержней приложены к точке D - вершине трехгранной пирамиды, образуемой треногой. На точку D действуют вертикально вниз и горизонтально влево силы натяжения ветвей троса, равные силе тяжести груза F, а также три реакции R_A, R_B и R_C стержней треноги.

2. Систему пяти сил, действующих на точку D, в выбранных осях координат изобразим на рис. 1, б; реакции R_A, R_B и R_C стержней направлены вдоль стержней от точки D (из предположения, что все стержни растянуты).

3. Прежде чем приступить к составлению уравнений равновесия, следует заметить, что силы, лежащие в плоскости, перпендикулярной какой-либо оси, проецируются на эту ось в виде точки (т.е. проекции равны нулю). Например, обе силы F (вертикальная и горизонтальная) и сила R_C лежат в плоскости, перпендикулярной оси Х. Поэтому на ось Х проецируются лишь силы R_A и R_B. Рассуждая аналогично, видим, что на ось Y проецируются все силы, кроме вертикальной силы F, и на ось Z - также все силы, за исключением горизонтальной силы F.

Составим уравнения равновесия:

(1)

(2)

(3)

Так как ADK = BDK = KDO = 30° и ODC = 45°, из уравнения (1) находим, что R_A = R_B.

Уравнения (2) и (3) запишем теперь в виде

Складывая эти уравнения и учитывая, что sin30° = 0,5 и , получаем

откуда

кН.

Стержни AD и BD треноги сжаты силой 8,44 кН.

Теперь, зная R_A, найдем

кН.

Стержень CD растянут силой 3,82 кН.

Ответ: кН; кН; кН.

Пример 10. Определить усилия в стержнях пространственной фермы, изображенной на рис. 1, а также реакции опор фермы Е, F, К и L, если на узел В фермы действует вертикальная сила F₁ = 50 кН, на узел С - горизонтальная сила F₂ = 25 кН, направленная вдоль стержня CD. Размеры указаны на рисунке.

Рис.1

Решение. Для определения усилий в стержнях 1-12 фермы воспользуемся способом вырезания узлов. Так как силы, действующие на каждый из узлов фермы, взаимно уравновешиваются, то, вырезая отдельные узлы фермы, составляем по три уравнения равновесия сил, действующих на каждый узел.

Узлы фермы вырезаем в такой последовательности, при которой число неизвестных сил в рассматриваемом узле не превышает трех. Так же, как и при определении усилий в стержнях плоских ферм, все стержни фермы условимся считать растянутыми; знак «минус» у вычисленной реакции стержня покажет, что стержень сжат.

Для определения усилий в стержнях рассматриваемой фермы будем вырезать последовательно узлы А, В, С и D (рис. 2).

Узел А:

(1)

(2)

(3)

Так как узел А не загружен внешней силой, а сходящиеся силы N₁, N₂ и N₆, не лежащие в одной плоскости, не могут уравновешиваться, то они равны нулю.

Рис. 2

Узел В:

(4)

(5)

кН. (6)

Из уравнения (5)

Из уравнения (4)

Узел С:

(7)

кН; (8)

(9)

Из уравнения (7)

Из уравнения (9)

Узел D:

(10)

(11)

(12)

Найдем синусы и косинусы углов и .

Так как

AD = DL, тo = 45°;

cos = АВ / DB = 4 / 5 = 0,8;

sin = AD / DB = 3 / 5 = 0,6.

Из уравнения (10)

Из уравнения (11)

кН.

Из уравнения (12)

кН.

Таблица 1. Результаты расчётов

Стержни	1	2	3	4	5	6	7	8	9	10	11	12
Усилие N, кH	0	0	0	-25	0	0	0	-19	31	0	0	-50

Основываясь на результатах расчета, можно установить следующее:

1. Если в незагруженном узле фермы сходятся три стержня, не лежащие в одной плоскости, то усилия в каждом из этих стержней равны нулю (узел А, стержни 1, 2 и 6).

2. Если в некотором узле фермы все внешние силы и все стержни, кроме одного, лежат в одной плоскости, то усилие в стержне, не лежащем в этой плоскости, равно нулю (узел С, стержень 11 при ).

Эти соображения, дающие возможность без вычислений определить стержни с нулевыми усилиями, значительно упрощают определение усилий в стержнях пространственных ферм.

Определив усилия в стержнях фермы способом вырезания узлов, можно определить реакции опор, представляющих собой шаровые шарниры. Реакцию каждой опоры неизвестного направления разложим на три составляющие, направленные вдоль осей координат. Эти составляющие определим из уравнений равновесия сил, приложенных к опорным узлам.

Узел Е:

(13)

(14)

(15)

Из уравнения (13)

Из уравнения (15)

Так как

то R_E = 0, т. е. опора Е не нагружена.

Узел F:

(16)

(17)

(18)

Из уравнения (16)

Из уравнения (18)

кН.

Знак «плюс» в ответе указывает на то, что истинное направление составляющей R_FZ совпадает с направлением, указанным на схеме.

Так как R_F_Х = 0 и R_FY = 0, то реакция опоры направлена вертикально вверх и имеет модуль R_F = |R_FZ| = 50 кН.

Узел К:

(19)

(20)

(21)

Из уравнения (20)

кН.

Из уравнения (4.47)

кН.

Знаки ответов показывают, что принятое направление силы R_KY совпадает с действительным, а силы R_KZ - противоположно действительному (см. рис. 2).

Определим модуль и направление реакции R_K:

кН;

Узел L:

Так как в узле L не известна лишь реакция R_L, то составляем только одно уравнение:

откуда

кН.

Знак «плюс» в ответе указывает на то, что реакция R_L направлена вертикально вверх.

Ответ: кН; кН; кН.

Пример 11. Жестко заделанная балка длиной l = 1,4 м и квадратным поперечным сечением со стороной a = 0,2 м (рис. 1, а) нагружена горизонтальной силой F = 2 кH и вертикальной равномерно распределенной нагрузкой интенсивностью q = 1 кН/м. Определить реакции заделки.

Рис. 1

Решение.

1. Освободим балку от заделки. Известно, что со стороны заделки на балку действуют реактивные силы и пара сил. Реактивную силу представим в виде трех составляющих R_OX, R_OY, R_OZ (рис. 1, б), действующих вдоль осей координат, а реактивный момент - в виде моментов пар M_OX, M_OY, M_OZ, действующих в плоскостях, перпендикулярных осям (эти моменты изображены на рис. 1, б круговыми стрелками, огибающими оси против хода стрелки часов, если смотреть со стороны положительного направления оси).

2. Равномерно распределенную нагрузку заменим сосредоточенной силой:

кН.

3. Составим уравнения равновесия:

4. Решая уравнения, находим:

кН; кН; ;

кН×м; кН×м; кН×м.

5. По найденным модулям составляющих реактивной силы R_O и момента реактивной пары M_O (они показаны на рис. 1, в раздельно) можно определить их модули R_O и M_O и направление действия.

кН;

кН×м; .

Ответ: кН; кН.

Пример 12. На валу жестко закреплены шестерня 1 и колесо 2 (рис. 1, а). Определить в положении равновесия вала реакции подшипников А и В, а также силы F₂ и = 0,4F₂, действующие на колесо, если F₁ = 400 Н, а = 0,4F₁. Силой тяжести вала, шестерни и колеса пренебречь.

Рис.1

Решение. Отбрасываем связи вала (подшипники), прикладываем к валу их реакции, разложенные на составляющие , , , . Выбираем пространственную систему координат так, чтобы ось X располагалась по оси вала, ось Y – параллельно силам и и ось Z – силам и . В точках А и В будут приложены реакции связей: в точке А - и , а в точке В - и (рис. 1, б).

Составляем уравнения равновесия сил, произвольно расположенных в пространстве:

(1)

(2)

(3)

(4)

(5)

Из уравнения (3)

Н.

Из уравнения (5)

Н.

Из уравнения (4)

Н.

Из уравнений (1) и (2):

Н;

Н.

Следует отметить, что уравнение даст тождество 0 = 0.

Полная реакция опоры А

Н.

Полная реакция опоры В

Н.

Ответ: Н; Н.

Пример 13. На валу жёстко закреплены шестерня 1 и колесо 2. Определить в положении равновесия вала реакции подшипников А и В, а также силы и , действующие на колесо, если Н, а . Силой тяжести вала, шестерни и колеса пренебречь.

Рис.1

Решение. Освобождаем вал от связей (подшипников) в точках А и В, заменим связи реакциями связей. Выбираем пространственную систему координат с началом в точке А, чтобы ось X располагалась по оси вала, ось Y – параллельно силам и и ось Z – параллельно силам и . В точках А и В будут приложены реакции связей, располагающиеся параллельно внешним силам, приложенным к валу в точках, а именно: в точке А - и , а в точке В - и (рис. 1, б).

Составляем уравнения равновесия сил, произвольно расположенных в пространстве:

(1)

(2)

(3)

(4)

(5)

Из уравнения (3)

Н.

Из уравнения (4)

Н.

Из уравнения (5)

Н.

Из уравнения (1)

Н.

Из уравнения (2)

Н.

Следует отметить, что уравнение даст тождество 0 = 0.

Полная реакция опоры А

Н.

Полная реакция опоры В

Н.

Ответ: Н; Н.

Пример 14. На барабан, закрепленный на валу, действует груз G. Какую силу F следует приложить к рукоятке CD, чтобы удержать вал в равновесии в положении, показанном на рис. 1, а? Определить также реакции подшипников А и В.

Рис.1

Решение. На вал действуют сила тяжести груза G, реакции опор , и пара сил с моментом М на рукоятке (рис. 1, б). Выберем систему координат и составим уравнение равновесия вала

Нм.

Сила на рукоятке

Н.

Определим реакции опор и :

Н.

Ответ: Н; Н; Н.

Пример 15. На барабан, закрепленный на валу, действует груз G. Какую силу F следует приложить к рукоятке CD, чтобы удержать вал в равновесии в положении, показанном на рис. 1, а? Определить также реакции подшипников А и В.

Рис. 1

Решение. На вал действуют сила тяжести груза G, реакции опор , и пара сил с моментом М на рукоятке (рис. 1, б). Выберем систему координат и составим уравнения равновесия вала:

Нм.

Если принять длину рукояти м, то сила на рукоятке

Н.

Определим реакции опор и :

Н.

Ответ: Н; Н; Н.

Пример 16. На барабан, закрепленный на валу, действует груз G. Какую силу F следует приложить к рукоятке CD, чтобы удержать вал в равновесии в положении, показанном на рис. 1, а? Определить также реакции подшипников А и В.

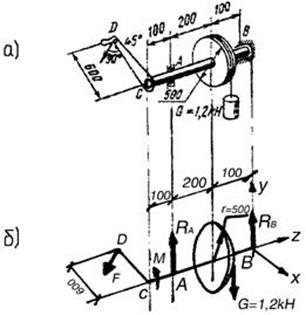
Рис. 1

Нм.

Если принять длину рукояти м, то сила на рукоятке

Н.

Определим реакции опор:

Н.

Ответ: кН; Н; Н.

Пример 17. Однородная квадратная крышка ABCD люка может вращаться вокруг оси, проходящей через петли А и В. Горизонтальная веревка DE удерживает крышку в равновесии в положении, показанном на рис. 1, а. Определить реакции опор А и В, если сила тяжести крышки G = 48 H.

Рис. 1

Решение. Внешние связи для пластины – шарниры в точках А, В и нить. Заменим их реакциями связей. Реакции петель А и В представим в виде двух составляющих , и , соответственно, а реакцию нити N направим вдоль линии DE (рис. 1, б).

Уравнения равновесия:

(1)

(2)

(3)

(4)

(5)

Из уравнения (5) системы

Из уравнения (4)

Н.

Из уравнения (1)

Н.

Из уравнения (3)

Н.

Из уравнения (2)

Н.

Полная реакция шарнира В

Н.

Ответ: Н; Н.

Пример 18. Полка, нагруженная, как показано на рис. 1, а, силой тяжести G = 0,8 кH и могущая вращаться около оси, проходящей через петли А и В, удерживается в равновесии в горизонтальном положении стержнем DC, образующим с вертикалью угол 60°. Определить реакции петель А, В и стержня DC.

Рис. 1

Решение. Внешние связи для пластины – шарниры в точках А, В и стержень. Заменим их реакциями связей. Реакции петель А и В представим в виде двух составляющих , и , соответственно, а реакцию стержня N направим вдоль линии DС (рис. 1, б).

Для составления уравнений равновесия силу N удобно разложить на две составляющие, одна из которых, , параллельна оси Z, другая, , расположена в плоскости XOY параллельно оси X. При этом , .

Уравнения равновесия:

(1)

(2)

(3)

(4)

(5)

Из уравнения (4)

Н.

Из уравнений (1) и (5) следует:

;

; Н;

Н.

Из уравнений (2) и (3) следует:

;

Н;

Н.

Полная реакция петли А

Н.

Полная реакция петли В

Н.

Ответ: Н; Н; Н.

Пример 19. На вал жестко насажены шкив 1 и колесо 2, нагруженные, как показано на рис. 1, a. Определить силы и , а также реакции опор А и В, если F₁ = 120 H.

Рис. 1

Решение. Отбрасывая связи вала (подшипники), прикладываем к валу их реакции, разложенные на составляющие , и , (рис. 1, б).

Составляем уравнения равновесия сил, произвольно расположенных в пространстве:

(1)

(2)

(3)

(4)

(5)

Из уравнения (4)

Н.

Из уравнения (5)

Н.

Из уравнения (3)

Н.

Из уравнения (1)

Н.

Из уравнения (2)

Н.

Следует отметить, что уравнение даст тождество 0 = 0.

Полная реакция опоры А

Н.

Полная реакция опоры В

Н.

Ответ: Н; Н; Н; Н.

Пример 20. На вал жестко насажены шкив 1 и колесо 2, нагруженные, как показано на рис. 1, a. Определить силы и , а также реакции опор А и В, если F₁ = 100 H.

Рис. 1

Решение. Отбрасывая связи вала (подшипники), прикладываем к валу их реакции, разложенные на составляющие , , и , (рис. 1, б).

Составляем уравнения равновесия сил, произвольно расположенных в пространстве:

(1)

(2)

(3)

(4)

(5)

Из уравнения (4)

Н.

Из уравнения (5)

Н.

Из уравнения (3)

Н.

Из уравнения (2)

Н.

Из уравнения (4.73)

Н.

Следует отметить, что уравнение даст тождество 0 = 0.

Полная реакция опоры А

Н.

Полная реакция опоры В

Н.

Ответ: Н; Н; Н; Н.

Пример 21. На вал жестко насажены шкив 1 и колесо 2, нагруженные, как показано на рис. 1, a. Определить силу , а также реакции опор А и В, если F₁ = 220 H.

Рис. 1

Составляем уравнения равновесия сил, произвольно расположенных в пространстве:

(1)

(2)

(3)

; (4)

(5)

Из уравнения (4)

Н.

Из уравнения (5)

Н.

Из уравнения (3)

Н.

Из уравнения (1)

Н.

Из уравнения (2)

Н.

Следует отметить, что уравнение даст тождество 0 = 0.

Полная реакция опоры А

Н.

Полная реакция опоры В

Н.

Ответ: Н; Н; Н.

Пример 22. Горизонтальный провод АЕ, натяжение которого равно 400 Н, подвешен к вертикальному столбу АВ, укреплённому оттяжками АС и АD, расположенными симметрично относительно плоскости ВАЕ. Известно: АВ = 5 м, ВС = BD = 4 м, СВD = 150°. Определить натяжение оттяжек и усилие в столбе (рис. 1, а).

Рис. 1

Решение. Рассмотрим равновесие сходящихся сил, приложенных к узлу А. Задаваемая сила N – реакция провода АЕ, реакция столба АВ и реакции N₁ и N₂ оттяжек АС и AD не лежат в одной плоскости. Три неизвестные силы , N₁ и N₂ определим из трёх уравнений равновесия сходящихся сил в пространстве:

Для этого проведём оси координат из точки В, направив ось Z вдоль ВА, ось Y – параллельно АЕ и ось Х - перпендикулярно осям Y и Z (рис. 1, б). Приложим к узлу А все действующие на него силы, направив их от узла, т. е. предположив, что все элементы растянуты. При проецировании сил N₁ и N₂ на оси Х и Y применим двойное проецирование, так как углы, составленные этими силами с осями Х и Y, не даны. Спроецируем сначала каждую из этих сил на плоскость XBY и полученную проекцию спроектируем на соответствующую ось.

Вычислим предварительно

Составим уравнения равновесия сил:

(1)

(2)

(3)

Из уравнения (1) получаем

N₁ = N₂.

Из уравнения (2) найдём эти силы:

Н.

N₁ = N₂ = 1235,5 Н (натяжения симметричных оттяжек одинаковы).

Из уравнения (3) определим :

Н.

Вертикальный столб АВ сжат.

Ответ: Н; Н.

Пример 23. Определить усилия в стержне пространственной фермы, изображённой на рис. 1, а также реакции опор фермы K, L, M, N, если на узел А фермы действуют вертикальная сила кН и горизонтальная сила кН, направленная вдоль стержня AF,

Рис. 1

Решение. Для определения усилий в стержнях 1-39 фермы воспользуемся способом вырезания узлов. Так как силы, действующие на каждый из узлов фермы, взаимно уравновешиваются, то, вырезая отдельные узлы фермы, составляем по три уравнения равновесия сил, действующих на каждый узел.

Для определения усилий в стержнях рассматриваемой фермы будем вырезать последовательно узлы А, В, С, D, E, F, H, I, J, K, L (см. рис. 1).

Для определения усилий в стержнях пространственной фермы воспользуемся способом вырезания узлов (рис. 2).

Узел А:

кН.

Узел В:

;

В силу симметрии

; ;

кН;

; кН.

Рассматривая узлы C и D, получим:

- усилия в стержнях 9 и 10 равны нулю.

: ,

кН.

: ,

кН.

Узел D:

(IHCD – квадрат);

кН.

В силу симметрии для узла С

кН; кН.

Узел E:

;

кН.

кН;

кН.

В силу симметрии для узла F

кН; кН; .

, кН.

Узел H:

кН;

кН.

Для узла I в силу симметрии

кН; кН;

кН.

, кН.

Узел J:

кН;

кН.

Для узла G в силу симметрии

кН; кН;

кН.

Основываясь на результатах расчета, можно установить следующее:

1. Если в незагруженном узле фермы сходятся три стержня, не лежащие в одной плоскости, то усилия в каждом из этих стержней равны нулю.

2. Если в некотором узле фермы все внешние силы и все стержни, кроме одного, лежат в одной плоскости, то усилие в стержне, не лежащем в этой плоскости, равно нулю.

Узел K:

;

кН; .

; кН.

; .

Узел L:

;

кН; .

кН.

;

кН;

кН; .

кН.

Для узла М в силу симметрии

кН;

кН.

Результаты расчётов сводим в табл. 2.

Рис. 4.30. К примеру 119

Таблица 2. Результаты расчётов

Стержни	1	2	3	4	5	6	7
Усилие N, кH	20	20,706	20,706	-11,547	-11,547	5,774	5,774

Стержни	8	9	10	11	12	13	14
Усилие N, кH	3,0	0	0	10,718	-6,356	-6,356	10,072

Стержни	15	16	17	18	19	20	21
Усилие N, кH	10,072	-22,736	-22,736	26,076	26,077	14,142	-10

Стержни	22	23	24	25	26	27	28
Усилие N, кH	-10	9	14,142	-6,372	10,083	-6,372	10,083

Стержни	29	30	31	32	33	34	35
Усилие N, кH	31,644	14,142	18,496	-22,015	-22,015	18,496	14,142

Стержни	36	37	38	39
Усилие N, кH	4,506	15,576	-10	-10

Реакции шарниров:

кН; кН;

кН; кН.

Рис. 3

Сделаем проверку по методу сечений:

В – точка Риттера.

; ;

; .

;

кН; кН.

; ; , кН.

Пример 24. Определить реакции опор пространственной системы.

Дано: вариант расчетной схемы (рис. 1).

Р₁ = 8 кН; Р₂ = 12 кН; q = 6 кН/м;

М = 16 кНм; АВ = 0,8 м; ВС = 0,6 м; CD = 0,5 м;

BC || AZ; CD || AX; M ^ AY; q || AZ; P₁ ^ AX; P₂ ^ AZ.

Рис. 1

Решение. Расставляем реакции опор. Если опора одна и она является жесткой заделкой в точке А, то такая опора запрещает перемещение вдоль всех трех осей и поворот конструкции вокруг этих осей. Поэтому возникают три реакции в виде сил , выбираемых по осям, и три реакции в виде пар сил с моментами , перпендикулярными осям. Если опор более одной, то последние пары сил перераспределяются между ними и, например, в шарнирных опорах остаются только реакции в виде сил, направленных вдоль соответствующей оси, если опора запрещает перемещение в этом направлении. Если одной из опор является невесомый рычаг или трос, или опорная плоскость, то реакция одна - как на рис. 2.

Рис. 2

Далее схема решения аналогична примененной ранее для плоских систем (она типична для любой задачи статики). То есть, определяем силу Q, раскладываем все силы на составляющие параллельные осям, используя для этого исходные данные, а именно: то, каким осям параллельна или перпендикулярна данная нагрузка. Затем составляем шесть уравнений равновесия, начиная с уравнений моментов относительно осей, и решаем полученную систему алгебраических уравнений относительно значений искомых реакций (знак реакции, как обычно, говорит о правильности первоначально выбранного её направления).

В заключение отметим, что момент относительно выбранной оси создают только те силы или составляющие, а также пары сил, которые перпендикулярны ей и не пересекают ось. Наоборот, проекцию на выбранную ось дают только параллельные ей составляющие сил.

Пример 25. Шесть невесомых стержней 1, 2,…6 соединены своими концами шарнирно в узлах (рис.1). В узле L приложена сила , в узле М – сила Q =50 Н. Сила образует с положительными направлениями координатных осей Х, У, Z углы, равные соответственно =45⁰, =60⁰, =60⁰, а сила углы =60⁰, =45⁰, =60⁰.

Грани параллелепипеда, параллельные плоскости ХУ, – квадраты. Диагонали других (боковых) граней образуют с плоскостью ХУ угол =60⁰, а диагональ параллелепипеда образует с этой плоскостью угол . Определить усилия в стержнях.

Дано: Р =250 Н, Q =50 Н, =45⁰, =60⁰, =60⁰, =60⁰, =45⁰, =60⁰, =60⁰.

Определить: N₁, N₂, N₃, N₄, N₅, N₆.

Указания. Задача – на равновесие пространственной системы сходящихся сил. При ее решении следует рассмотреть отдельно равновесие каждого из двух узлов, где сходятся стержни и приложены заданные силы, и учесть закон о равенстве действия и противодействия; начинать нужно с узла, где сходятся три стержня.

Решение. Рассмотрим равновесие узла L (рис. 2), в котором сходятся стержни 1, 2, 3. реакции стержней направим от узла, считая стержни растянутыми. Получим систему сходящихся сил. Узел L находится в равновесии, если равнодействующая приложенных к нему сил =0, т.е. силовой пространственный многоугольник должен быть замкнутым. Однако построение его на плоском чертеже затруднительно. Эту задачу можно значительно проще решить аналитическим методом через проекции на оси координат.

; ;

Рис.1

Рис.2

Проектируя силы на координатные оси, получим систему уравнений:

на ось Х: Pcos –N₁ – N₃ sin45⁰ =0; (X);

на ось У: Pcos +N₃cos45⁰ + N₂ cos =0; (Y);

на ось Z: Pcos - N₂sin=0; (,Z).

Решением этой системы уравнений является:

N₁ =373,87 Н; N₂ =144,51 Н; N₃ = -278,82 Н.

Рассмотрим равновесие узла М (рис. 3), в котором сходятся стержни 1, 4, 5 и 6.

Рис.3

На узел действуют сила и реакции стержней . заметим сразу же, что по закону о равенстве действия и противодействия .

Для дальнейших расчетов определим сначала угол , образованный диагональю параллелепипеда (стержень 4) с плоскостью ХУ.

Пусть длина стороны квадратного основания равна а. Тогда из прямоугольного ABL длина AL равна 2а, из прямоугольного ALМ длина АМ (стержень 4) равна а. Но АМ является гипотенузой в прямоугольном треугольнике AСМ, катет которого АС – диагональ квадрата основания, и поэтому его длина равна а. Следовательно: cos =/= 0,632, sin0,775.

Qcos + N^/₁ + N₄cos sin45⁰ + N₅cos=0.

Qcos + N₄coscos45⁰ =0.

Qcos – N₅sin–N₆ – N₄sin =0.

Решением этой системы уравнений является:

N₄ = -79,11 Н; N₅ = -727,24 Н; N₆ = -570,76 Н.

Ответ:

N₁ =373,87 Н – стержень 1 растянут;

N₂ =144,51 Н – стержень 2 растянут;

N₃ = -278, 82 Н – стержень 3 сжат;

N₄ = -79,11 Н – стержень 4 сжат;

N₅ = -727,24 Н – стержень 5 сжат;

N₆ = -570,76 Н – стержень 6 сжат.

Пример 26. Две однородные прямоугольные плиты, сваренные под прямым углом друг к другу, закреплены сферическим шарниром в точке А, цилиндрическим подшипником в точке В и невесомым стержнем 1 (рис. 1). Стержень 1 прикреплен к плите (в точке Д) и к неподвижной опоре (в точке С) шарнирно.

Размеры плиты в направлениях, параллельных координатным осям, равны x₁= 1,5 м, y₁= 2,5 м, z₁= 1 м. Вес большей плиты Р₁ = 5 кН, вес меньшей плиты Р₂ = 3 кН.

На плиты действуют: пара сил с моментом М=3 кНм, лежащая в плоскости большей плиты, и две силы F₁= 15 кН, F₂ = 18 кН. Сила расположена в плоскости xy и составляет угол = 30⁰ с осью x. Сила расположена в плоскости, параллельной xz, и составляет угол = 45⁰ с осью z.

Определить реакции опор в точках А, В и стержня СД.

Дано: x₁ = 1,5 м, y₁ = 2,5 м, z₁ = 1 м, P₁ = 5 кН, P₂ = 3 кН, M = 3 кНм, F₁ = 15 кН, F₂ = 18 кН, =30⁰, =45⁰, =30⁰.

Определить: X_A, Y_A, Z_A, Y_B, Z_B и N.

Рис.1

Указания. Задача – на равновесие тела под действием произвольной пространственной системы сил. При ее решении учесть, что реакция сферического шарнира (подпятника) имеет три составляющие (по всем трем координатным осям), а реакция цилиндрического шарнира (подшипника) – две составляющие, лежащие в плоскости, перпендикулярной оси шарнира (подшипника). При вычислении момента силы часто удобно разложить ее на две составляющие и , параллельные координатным осям (или на три); тогда, по теореме Вариньона, и т.д.

Решение.

1. Рассмотрим равновесие тела, состоящего из двух сварных плит (рис. 1).

2. На тело действуют: сила в точке Е, сила в точке C₂, сила тяжести в точке С₁, сила тяжести в точке C₂ (рис. С4а).

3. Реакции связей – в сферическом шарнире: ; в цилиндрическом подшипнике: , реакция невесомого стержня направлена вдоль стержня (см. рис. 2). На данном этапе решения задачи направления реакций назначаем произвольно, при этом предполагаем, что стержень 1 растянут.

4. В задаче шесть неизвестных реакций, следовательно, задача статически определимая.

Рис.2

6. Составим шесть уравнений равновесия полученной пространственной системы сил. При вычислении моментов сил относительно координатных осей применяется теорема Вариньона, согласно которой момент силы относительно оси равен сумме моментов составляющих этой силы относительно той же оси.

Подставив в составленные уравнения числовые значения всех заданных величин и решив эти уравнения, найдем искомые реакции.

Ответ: X_A = 0,26 кH, Y_A = -45,69 кH, Z_A = -28,8 кH, Y_B = =6,84 кН, Z_B = 6,1 кН, N = 36,2 кН.

Пример 27. Конструкция состоит из невесомых стержней 1, 2, …, 6, соединенных друг с другом (в узлах К и М) и с неподвижными опорами А, В, С, D шарнирами (рис. 1). В узлах К и М приложены силы и , образующие с координатными осями углы , , , и , , соответственно (на рисунке показаны только углы , , ).

Дано: Р = 100 Н, = 60°, = 60°, = 45°; Q = 50 Н, = 4 5°, = 60°, = 60°, = 30°, = 60°, = 74°.

О п р е д е л и т ь : усилия в стержнях 1-6.

Рис.1

Указания. Задача - на равновесие пространственной системы сходящихся сил. При ее решении следует рассмотреть отдельно равновесие каждого из двух узлов, где сходятся стержни и приложены заданные силы, и учесть закон о равенстве действия и противодействия; начинать с узла, где сходятся три стержня.

Изображать чертеж можно без соблюдения масштаба так, чтобы лучше были видны все шесть стержней. Стержни следует пронумеровать в том порядке, в каком они указаны в таблице; реакции стержней обозначать буквой с индексом, соответствующим номеру стержня (например, ₁, ₂ и т.д.).

Решение. 1. Рассмотрим равновесие узла К, в котором сходятся стержни 1, 2, 3. На узел действуют сила и реакции ₁, ₂, ₃ стержней, которые направим по стержням от узла, считая стержни растянутыми. Составим уравнения равновесия этой пространственной системы сходящихся сил:

, P cos + N₂ sin + N₃ sin = 0; (1)

, P cos + N₁ –N₂ cos = 0; (2)

, P cos – N₃ cos = 0. (3)

Решив уравнения (1), (2), (3) при заданных числовых значениях силы Р и углов, получим N₁ = 349 Н, N₂ = -345 Н, N₃= 141 Н.

2. Рассмотрим равновесие узла M. На узел действуют сила и реакции ’₂, ₄, ₅, ₆ стержней. При этом по закону о равенстве действия и противодействия реакция '₂ направлена противоположно ₂, численно же N'₂ = N₂ . Составим уравнения равновесия:

, Q cos –N₂ sin - N₄ – N₅ sin sin = 0; (4)

, Q cos +N₂ cos + N₅ sincos = 0; (5)

, Q cos – N₅ cos - N₆ = 0. (6)

При определении проекций силы ₅ на оси X и Y в уравнениях (4) и (5) удобнее сначала найти проекцию '₅ этой силы на плоскость XOY (по числовой величине N'₅ = N₅ sin ), а затем найденную проекцию на плоскость спроектировать на оси X и Y.

Решив систему уравнений (4), (5), (6) и учитывая, что N’₂ = N₂ = - 345 Н, найдем, чему равны N₄, N₅, N₆.

О т в е т: N₁ = 349 Н; N₂ = -345 Н; N₃ = 141 Н; N₄ =50 Н; N₅ = 329 Н; N₆ = -66 Н. Знаки показывают, что стержни 2 и 6 сжаты, остальные - растянуты.

Пример 28. Горизонтальная прямоугольная плита весом Р (см. рис. 1) закреплена сферическим шарниром в точке А, цилиндрическим (подшипником) в точке В и невесомым стержнем DD’. На плиту в плоскости, параллельной XZ, действует сила , а в плоскости, параллельной YZ, - пара сил с моментом М.

Д а н о: Р= 3 кН, F= 8 кН, М= 4 кНм, = б0°, АС= 0,8м, АВ= 1,2 м, ВЕ= 0,4 м, ЕН= 0,4 м.

О п р е д е л и т ь: реакции опор А, В и стержня DD'.

Рис.1

Указания. Задача - на равновесие тела под действием произвольной пространственной системы сил. При её решении учесть, что реакция сферического шарнира (подпятника) имеет три составляющие (по всем трем координатным осям), а реакция цилиндрического шарнира (подшипника) - две составляющие, лежащие в плоскости, перпендикулярной оси шарнира (подшипника). При вычислении момента силы часто удобно разложить сё на две составляющие ’ и ”, параллельные координатным осям (или на три); тогда, по теореме Вариньона, m_x() = m_x(’) + m_x(”) и т.д.

Решение. 1. Рассмотрим равновесие плиты. На плиту действуют заданные силы , и пара с моментом M, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие _A, _A, _A, цилиндрического (подшипника) - на две составляющие _B, _B (в плоскости, перпендикулярной оси подшипника); реакцию стержня направляем вдоль стержня от D к D’, предполагая, что он растянут.

2. Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы:

, X_A + X_B + F cos 60° = 0;

, Y_A – N cos 30° = 0;

, Z_A + Z_B – P + N sin 30° - F sin 60° = 0;

, M – P 0,5 AB + Z_B AB – F sin 60° AB + N sin 30° AB = 0;

, P 0,5 AC – N sin 30° AC + F sin 60° 0,5 AC – F cos 60° BE = 0;

, - F cos 60° AB – N cos 30° AC – X_B AB = 0.

Для определения моментов силы относительно осей раскладываем ее на составляющие ’ и ”, параллельные осям X и Z (, ), и применяем теорему Вариньона. Аналогично можно поступить при определении моментов реакции .

О т в е т: X_A=3,4 кН; Y_A=5,1 кН; Z_A=4,8 кН; X_B=-7,4 кН; Z_B=2,1 кН; N=5,9 кН. Знак минус указывает, что реакция _B направлена противоположно показанной на рисунке.