Главная
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО СТАТИКЕ
Пример 1. Стержни АС
и ВС (рис. 1,а) соединены между
собой шарниром С,
а с вертикальной стеной — посредством шарниров
А и В. В шарнире С приложена
сила F = 1260 Н. Требуется определить реакции N1
и N2 стержней действующие на шарнир С, если 
= 30° и 
= 60°.
Рис. 1
Решение. Рассматриваем равновесие точки С, которая
считается несвободной, так как на нее наложены связи в виде стержней АС и ВС.
Освобождаем точку С
от связей и заменяем их силами реакций связей, считая, что стержень АС растягивается, а стержень ВС сжимается под действием силы F. Обозначим реакцию стержня АС через N1, а реакцию стержня ВС через N2.
В итоге точка С
становится свободной, находясь под действием плоской системы трех сходящихся
сил: активной силы F и сил реакций N1
и N2 (рис. 1, б). Приняв точку О за начало координат, перенесем
силы F, N1 и N2
параллельно самим себе в эту точку (рис. 1, в) и составляем уравнения
проекций сил на оси координат:
или
(1)
и
. (2)
Умножим
уравнение (1) на 
, получим
(3)
. (4)
После сложения
уравнений (3) и (4) получим
откуда 2N2 = F или 
Н. Из уравнения
(1) получаем, что
или 
Н.
Графический метод. Для решения задачи
этим методом выбираем масштаб силы F (например, 10 Н = 1 мм)
и строим замкнутый треугольник сил (рис. 1, г). Из произвольной точки О проводим
прямую, параллельную вектору F, и откладываем на этой
прямой в выбранном масштабе вектор 
. Из конца вектора (точка А) проводим прямую, параллельную вектору
, а из точки О —
прямую, параллельную вектору 
. Пересечение этих прямых дает точку В. Получили замкнутый треугольник сил ОАВ, стороны которого в выбранном масштабе изображают силы,
сходящиеся в точке С. Величины сил N1и
N2 определим после измерения сторон АВ и ВО треугольника ОАВ.
Ответ: N1 = 1089,9 H;
N2 = 630 H
Пример 2. К вертикальной стене АВ на тросе АС подвешен шар с центром О (рис. 1, а) и весом F = 120 Н. Трос
составляет со стеной угол = 30°. Определить реакции N натяжения троса и давления
шара в точке D стены АВ.
Рис. 1
Решение. Рассмотрим равновесие точки О. Освобождая ее от
связей (трос АС и стена АВ), получим в этой точке плоскую систему
трех сходящихся уравновешенных сил: F, N и RD, при этом реакция N направлена по тросу, а реакция RD
- перпендикулярно стене АВ.
Приняв точку О
за начало координат, перенесем в эту точку силы F, N и RD параллельно самим себе
и спроецируем силы на оси Х и Y (рис. 2, б). Уравнения равновесия будут иметь вид
или
(1)
(2)
Из уравнения (2)
Из уравнения
(1)
Н.
Ответ: N = 138,6
H; 
= 69,3 H.
Пример 3. Два жестких стержня АВ и АС
имеют общую шарнирную точку А и шарнирные опоры В
и С (рис. 1, а). Сила F = 500 Н приложена к шарнирному валику в
точке А. Стержни АВ и АС образуют углы по 30° с
линией действия силы F. Определить усилия в стержнях.
а) б) в)
Рис. 1
Решение. Сила F приложена в точке А, которая находится в равновесии под действием силы F и реакции стержней АВ
и АС. Реакции стержней направлены
вдоль их осей.
Рассмотрим равновесие точки А.
Отбросив связи точки А и
заменив их реакциями стержней АВ и АС (рис. 1, б), получим систему
сходящихся сил. Из точки А
проведём координатные оси. Ось Х
направим перпендикулярно силе F. Составим уравнение
равновесия (сумма проекций всех сил на ось Х
равна нулю):
,
откуда
NAB = NAC.
Сумма проекций
всех сил на ось Y также равна нулю:
,
откуда
Н.
В данном
примере силы NAC и NAB получились со знаком «плюс» (+), следовательно, действительное
направление сил совпадает с тем, которое предполагалось при составлении
уравнения. Если сила получится со знаком «минус» (-), то это значит, что ее действительное направление
противоположно тому, которое было намечено при составлении уравнений
равновесия.
Мы определили
величину, а также направление реакций стержней, приложенных к точке A. К верхним концам стержней приложены такие же по величине
силы, но противоположно направленные. К нижним концам стержней приложены силы
реакции опор В и С, равные по величине силам,
приложенным к верхним концам, и направленные им навстречу (рис. 1, в). Следовательно, оба стержня сжимаются силами
NAC = NAB = 288,7 H.
Ответ: NAC = NAB = 288,7 H.
Пример 4. Определить силы, нагружающие стержни АВ и АС
кронштейна, удерживающего в равновесии груз F = 6 кН и растянутую пружину, сила
упругости которой F1 = 2 кН. Весом частей
конструкции, а также трением на блоке пренебречь (рис. 1, а).
Рис. 1
Решение. Задачу решаем аналитическим методом.
Рассматриваем равновесие точки схода А.
К ней приложены заданные активные силы - сила натяжения троса АD, равная весу
груза F, и сила упругости пружины F1.
Так как и трос, и пружина растянуты, то эти силы направлены от точки А. Рассматривая точку A как свободную, отбрасываем связи
(стержни АВ и АС), заменяя их действие реакциями NAB
и NAC. Реакции стержней направляем от точки А, так как
предварительно полагаем стержни растянутыми (действительные направления реакций
стержней в начале решения неизвестны). Если наше предположение окажется
неверным, то искомая реакция стержня получится в ответе со знаком «минус»; это
говорит о том, что стержень сжат и истинное
направление реакции -
к точке А. Полученная расчетная схема
изображена на рис. 1, б.
Принимаем
обычное вертикально-горизонтальное направление координатных осей. Для
полученной плоской системы сходящихся сил составляем два уравнения равновесия:
1) 
2) 
Решая
полученную систему уравнений, находим 
и 
Искомые силы,
нагружающие стержни, по модулю равны найденным реакциям стержней, а по
направлению противоположны им. Замечаем, что в соответствии с изложенным
правилом стержень АВ оказался
растянутым, а стержень АС -
сжатым.
Следует
отметить, что каждое из полученных уравнений равновесия содержало оба
неизвестных, чего можно избежать, направив координатные оси по-другому — совместив одну из осей с неизвестной силой
(рис. 1, в). При этом в уравнении
равновесия для другой оси окажется лишь одно неизвестное:
откуда
и 
Для проверки
правильности решения применяем графический метод - в
выбранном масштабе строим замкнутый силовой многоугольник (рис. 1, г).
От произвольной точки откладываем вектор заданной силы F1,
от конца вектора 
-
вектор заданной силы .
Затем через начало и
конец вектора проводим известные направления искомых реакций стержней АВ и АС.
Стрелки, изображающие направления сил NAB и NAC, ставим таким образом, чтобы в
векторном многоугольнике было единое направление обхода - в данном случае против часовой стрелки. Измеряя
искомые векторы с учетом принятого масштаба, получаем 
и 
. (Точность
графического решения будет тем выше, чем крупнее принят масштаб построения). Следует отметить, что векторный
многоугольник показывает действительное, а не предполагаемое направление
искомых сил.
Ответ: 
; 
Пример 5.
Определить силу натяжения троса, удерживающего в равновесии шар весом G = 20
Н, а также силу давления шара на наклонную опорную плоскость (рис. 1, а).
Решение. Задачу решаем аналитическим методом.
К шару приложена заданная активная сила - вес
шара G. Отбрасываем связи (трос ВС и опорная плоскость), заменяя их действие реакциями NBC, RA.
Реакцию растянутого троса направляем от шара, а реакцию опорной плоскости - по
нормали к ней в сторону к шару (рис. 1, б).
Рассматриваем равновесие точки О схода всех сил. Полученная расчетная схема изображена на
рис. 1, в.
Рис. 1
Принимаем
обычное вертикально-горизонтальное направление координатных осей. Для
полученной плоской системы сходящихся сил составляем два уравнения равновесия:
1) 
2) 
Решая
полученную систему уравнений, находим 
и 
Искомая сила натяжения троса и сила давления шара на
плоскость соответственно равны найденным реакциям, а по направлению
противоположны им.
Решение задачи
при другом, более рациональном направлении координатных осей советуем выполнить
самим учащимся.
Для проверки правильности решения применяем
графоаналитический метод - строим замкнутый силовой треугольник
(рис. 1, г). От произвольной точки откладываем вектор заданной силы G, через
начало и конец которого проводим известные направления искомых реакций троса и
опоры. Построенный графическим методом силовой треугольник решаем аналитическим
методом - здесь удобно применить
известную из математики теорему синусов:
Решая
пропорции, получаем
кН;
кН.
Применение
графоаналитического метода решения целесообразно лишь для системы, состоящей из
трех сил.
Ответ: 
кН; 
кН.
Пример 6. Определить усилия в стержнях АВ и ВС
(рис. 1, а), если сила F, действующая на шарнир В, равна 50 кН;
вес груза G = 60 кН.
а)
б)
Рис. 1
Решение. Задачу решаем аналитическим методом.
К шарниру приложены активные силы — вес
груза G и сила F. Отбрасываем связи
(стержни АВ и ВС), заменяя их действие реакциями NАВ и NВС.
Реакции стержней направляем от точки В к точкам А и С соответственно, так как предварительно
полагаем стержни растянутыми (действительные направления реакций стержней в начале
решения неизвестны). Если наше предположение окажется неверным, то искомая
реакция стержня получится в ответе со знаком «минус»; это говорит о том, что
стержень сжат и истинное направление реакции противоположно. Рассматриваем
равновесие точки В
схода всех сил. Выбираем систему координат так, чтобы одна из осей совпала с
неизвестной силой. Полученная расчетная схема изображена на рис. 1, б.
Для полученной
плоской системы сходящихся сил составляем два уравнения равновесия:
1) 
2) 
.
Решая систему,
получаем:
кН;
кН.
Искомые силы,
нагружающие стержни, по модулю равны найденным реакциям стержней, а по
направлению противоположны им. Замечаем,
что в соответствии с изложенным правилом стержни ВА и ВС оказались
растянутыми.
Проверка. Так как шарнир В находится в
равновесии, то
.
Мы получили верное равенство, значит, задача решена верно.
Ответ: 
кН; 
кН.
Пример 7. Определить силу давления
ступенчатой колонны (рис. 1, a) на горизонтальную опору и силы
взаимодействия частей колонны по сечению А-А. Сила
тяжести (вес) верхней части колонны F1 = 30 кH, нижней F2 = 60 кН.
Решение. По условию задачи надо рассмотреть
равновесие колонны. Точки приложения сил F1 и F2 - в центре тяжести каждой части колонны. Действуют эти силы по одной
вертикальной прямой - вниз, их модули заданы.
Опора колонны - горизонтальная плоскость,
препятствующая ее перемещению по вертикали вниз. Действие опоры заменяем реакцией
R, направленной вертикально вверх (рис. 1, б). Рассматриваемое тело находится в равновесии
под действием трех сил, направленных по одной прямой. Для определения
неизвестной силы реакции опоры применим уравнение равновесия.
Удобнее всего
расположить оси координат таким образом, чтобы одна ось совпадала по
направлению с силами R, F1
и F2, тогда получится одно уравнение равновесия (на
ось X все силы
проектируются в точку):
следовательно,
R = F1 + F2 = 30 +60 =90
кН.
а) б) в) г)
Рис. 1
Сила давления
колонны на опору R' (в соответствии с аксиомой о том, что действие равно
противодействию) равна по модулю реакции R, но направлена в
противоположную ей сторону - вниз (рис. 1, в). Чтобы определить силы
взаимодействия частей колонны по сечению А-А,
мысленно разделим обе части колонны и действие одной части на другую заменим
силами, как показано на рис. 1.23, г.
Рассмотрим
равновесие одной части колонны, например верхней:
кН.
На основании
аксиомы о равенстве действия и противодействия сила 
кН. Тот же результат
получится, если рассмотреть равновесие нижней части колонны:
NA = R - F2 = 90 - 60 = 30 кH.
Ответ: 
кН; 
кН.
Пример 8. Определить опорные реакции, возникающие при
действии на брус силы F = 50 кН (силой тяжести бруса можно пренебречь). Расстояние
между опорами 
= 2 м.
Сила приложена посредине между опорами под углом
45° к оси бруса в точке D (рис. 1, а).
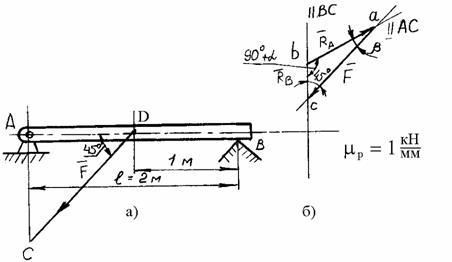
Рис. 1
Решение.
Рассмотрим равновесие бруса, опирающегося на вершину угла В и шарнир А. Действие опор заменим реакциями. Направление опорной реакции RB
перпендикулярно опорной плоскости. Точка С - пересечение линии
действия силы F и направления опорной
реакции RB.
Направление
опорной реакции A определяется на основании того,
что тело может находиться в равновесии под действием трех непараллельных сил
только в случае, если линии действия всех трех сил пересекаются в одной точке.
Следовательно, опорная реакция шарнира A -
RA будет направлена по линии АС. Так как тело находится в равновесии под действием трех сил,
силовой треугольник должен быть замкнутым
(геометрическое условие равновесия). На рис. 1, б выполнено построение силового треугольника и графически
определены опорные реакции RA и RB.
Масштаб
построения силового треугольника 
= 1 кН/мм, т. е. 1 мм соответствует силе в 1 кН. Для определения сил следует длину стороны треугольника умножить на масштаб:
Графическое
решение можно проверить вычислением. Для этого надо найти стороны ab и bc силового треугольника abc. Прежде всего определим
углы и .
Угол a
можно определить из треугольника саb (рис. 1, б).
Согласно построению этот треугольник прямоугольный, а из треугольника CBD видно, что CB = BD = l / 2 = 1 м.
Следовательно, можно написать 
(рис. 1.24, б), отсюда = 26°30' и угол = 180° - 45° - 90° - = 45° -
26°30' = 18°30'.
На основании
теоремы синусов для треугольника abc
можно написать:
кН;
кН.
Небольшое
расхождение в величине опорных реакций объясняется меньшей точностью
графического метода решения.
Ответ: 
кН; 
кН.
Пример 9. Определить реакции стержней АВ и СВ,
общий шарнир В
которых нагружен, как показано на рис. 1, а, силами F1 = 0,5 кН и F2 = 1 кН.
а) б) в)
Рис. 1
Решение
1. Выделим точку, равновесие которой
следует рассмотреть, чтобы определить неизвестные реакции стержней. Здесь такой
точкой является шарнир В.
Изобразим его отдельно на рис. 1, б.
2. Изобразим действующие на точку В активные силы
(нагрузки) F1 и F2, действующие на шарнир В вдоль нитей, к которым прикреплен
каждый из грузов.
3. Мысленно освободим шарнир В от связей
(стержней) и заменим действие связей их реакциями NA
и NC, направленными вдоль стержней ВА и ВС
соответственно. Не всегда заранее можно определить, какой из стержней растянут
или сжат. Например, в данном случае груз F1
сжимает стержень ВА и растягивает
стержень BC, а груз F2 - наоборот: растягивает стержень ВА и сжимает стержень ВС.
Поэтому существует общепринятое правило считать предположительно все стержни
растянутыми. В соответствии с этим правилом реакции NA
и NB стержней на рис. 1.25, б направлены
от шарнира В
к связям.
4. Приняв точку В за начало координат, выберем
положение осей Х (ось абсцисс) и Y (ось ординат) таким образом, чтобы по крайней мере одна из
них совпала с линией действия неизвестной силы, т. е. совместив одну из
осей координат с осью какого-либо стержня. В данном случае (рис. 1, б) ось Х совмещена с осью стержня АВ (можно было бы ось Y совместить с осью стержня ВС).
5. Определив при помощи данных на рис.
1,а углы, образуемые силами F1, F2, NA, NC с осями Х
и Y, определим проекции всех сил на каждую из осей и составим
из этих проекций уравнения равновесия для плоской системы сходящихся сил:
(1)
(2)
6. Решаем получившуюся систему
уравнений. Благодаря тому, что ось Х
совпадает с осью стержня АВ, ось Y перпендикулярна к этому стержню. Проекция NA (реакция стержня АВ) на ось Y равняется нулю, и второе уравнение
содержит только одно неизвестное.
Из уравнения (2) имеем:
кН.
Знак «минус»
перед численным значением NC показывает,
что вектор NC (рис. 1,б) должен быть
направлен в противоположную сторону, т. е. стержень ВС не растянут, как предполагалось, а сжат силой 0,315 кН (315Н).
Из уравнения
(1) имеем:
откуда NA
= 0,6 кН.
Численное
значение NA положительно, значит,
предположительно выбранное направление вектора NA соответствует действительному
и стержень ВА растянут силой 0,6 кН
(600 Н).
7. Решение задачи обязательно следует проверить.
Лучшим способом проверки может быть либо решение с помощью иного выбора осей
координат (решите эту задачу, совместив ось Y с осью стержня ВС), либо решение задачи иным методом, например, графически.
Графическое
решение задачи (оно показано на рис. 1, в) выполнять очень просто с
помощью линейки с миллиметровой шкалой и транспортира. Из произвольной точки а
откладываем вертикально вниз (так направлена сила F1) вектор ab,
который в некотором масштабе 
, кН/мм, изображает силу F1.
Из точки b параллельно действию силы F2 на шарнир В в том же масштабе откладываем вектор bc, изображающий силу F2 (
). Затем из точек а
и с проводим прямые, параллельные
соответственно стержню АВ и стержню ВС. Эти прямые пересекаются в точке d. Образовался замкнутый многоугольник abcda, в котором сторона cd изображает реакцию стержня ВС, а сторона da -
реакцию стержня ВА
(
). Причем стрелки у этих сторон показывают,
который из стержней сжат или растянут.
Ответ: NA = 0,6 кН; NC = 0,315 кН.
Пример 10. Определить силу F, при
которой цилиндр весом 500 Н начнет вкатываться на наклонную плоскость, а также
реакцию наклонной плоскости (рис. 1,а). Трением пренебречь. Указание: в момент начала вкатывания
цилиндр отрывается от горизонтальной опорной плоскости.
а) б) в)
Рис. 1
Решение. Освобождаем тело (цилиндр) от связей
(наклонная плоскость), заменяя их действие на тело
реакциями G и R
(рис. 1, б). Рассмотрим равновесие точки О. В этой точке получим плоскую
систему трёх сходящихся уравновешенных сил: F, G и R, при этом
реакция R направлена перпендикулярно
наклонной плоскости (рис. 1, в). Приняв точку О за начало координат, перенесём
в эту точку силы F, G и R параллельно самим себе и спроецируем силы на оси X и Y. Уравнения равновесия будут иметь
вид
; (1)
. (2)
Выразив из
найденного уравнения (2) неизвестное R, получим
Н.
Тогда,
подставив значение R в уравнение (1), получим
Н.
Ответ: 
Н; 
Н.
Пример 11. Кулачковый
механизм состоит из кулачка треугольной формы, движущегося равномерно под
действием силы F = 80 Н и получающего вертикальное перемещение толкателя с роликом на
конце (рис. 1, а). В данном положении механизма ролик касается гипотенузы в ее середине. Определить реакцию
горизонтальной опорной поверхности и силу давления кулачка на ролик. Весом частей
механизма, а также трением пренебречь.
Решение. Освобождаем тело (кулачок) от связей
(толкатель с роликом и опорная поверхность), заменяя их действие
на тело реакциями (рис. 1, б) и рассмотрим равновесие точки D. Получим в ней плоскую систему трёх сходящихся
уравновешенных сил: F, RD,
и ROП, при этом реакция ROП направлена перпендикулярно опорной
поверхности, а реакция RD -
перпендикулярно гипотенузе кулачка (рис. 1, в). Принимаем точку D за начало координат и переносим в эту точку силы F, RD и ROП, спроецировав их на оси X и Y. Уравнения равновесия будут иметь
вид
; (1)
. (2)
Рис. 1
Из уравнения
(1)
Н.
Из уравнения (2)
Н.
Ответ: 
Н; 
Н.
Пример 12. Груз F = 17 кН равномерно поднимается с помощью троса, перекинутого
через блок B и наматываемого на барабан D лебедки (рис. 1, а). Определить силы, нагружающие стержни АВ и СВ кронштейна. Радиусом блока, весом
частей конструкции и трением на блоке пренебречь.
Рис. 1
Решение. Сила F приложена
в точке B. Реакция стержня АВ направлена вдоль её оси, а стержня ВС – по оси к точке С (рис. 1, б).
Рассмотрим
равновесие точки В. Отбросив связи
точки В и заменив их реакциями силы F и
стержней АВ и ВС, получим систему сходящихся сил с началом координат в точке В (рис. 1, в). Составим уравнения
равновесия:
,
откуда
. (1)
,
откуда
Н 
кН.
Подставляем
полученное значение 
в уравнение (1):
Н = 17 кН.
Ответ: 
кН; 
кН.
Пример 13. Под действием расположенной параллельно наклонной
плоскости сжатой пружины, сила упругости которой равна
3 Н, шарик перекрывает проходное отверстие пневматического клапана (рис. 1, а).
Определить силу F давления сжатого воздуха, при которой проходное отверстие откроется, а
также реакцию наклонной опорной поверхности. Весом частей механизма, а также
трением пренебречь. Указания:
в момент начала отжатия шарик отрывается от стенок
проходного отверстия.
Рис. 1
Решение. Освобождаем тело (шарик) от связей
(опорная поверхность и пружина), заменяя их действие на тело реакциями R и Fупр (рис. 1, б). Рассмотрим равновесие точки О, получим в ней
плоскую систему трех сходящихся уравновешенных сил: F, R и Fупр, при этом реакция R
направлена перпендикулярно наклонной плоскости. Принимаем точку О за начало
координат и, перенеся в эту точку силы F, R и Fупр, проецируем их на
оси X и Y (рис. 1, в). Уравнение равновесия
запишется в виде
. (1)
. (2)
Из уравнения
(2)
Н.
Из уравнения
(1)
Н.
Ответ: 
Н; 
Н.
Пример 14. Груз весом G = 6 кН с помощью наматываемого на барабан троса равномерно
перемещается вниз по наклонной плоскости (рис. 1, а). Приняв силу сопротивления
движению (силу трения) Fтр = 0,16G, определить силу
натяжения троса, а также нормальную реакцию опорной плоскости.
Рис. 1
Решение. Освобождаем тело (груз) от связи
(наклонная плоскость), заменяя её действие на тело
реакцией R (рис. 1, б). Рассмотрим равновесие
точки М и получим в ней плоскую
систему четырех сходящихся уравновешенных сил: G, R, Fтр
и N. Так же мы освобождались и от связи троса N. Точку М
принимаем за начало координат, перенеся в эту точку силы G, R, Fтр
и N параллельно самим себе и спроецировав их на оси X и Y, при этом реакция N направлена по тросу, а реакция R –
перпендикулярно наклонной плоскости (рис. 1, в). Ось X направляем вдоль реакции N. Составим
уравнения равновесия:
,
откуда
Н;
,
откуда
Н.
Ответ: 
Н; 
Н.
Пример 15. Определить силы, нагружающие стержни АВ и СВ кронштейна, удерживающего груз F = 11 кН (рис. 1,
а). Весом частей конструкции пренебречь.
Рис. 1
Решение. Сила
F приложена к точке В. Отбрасываем связи от точки В,
заменяем их реакциями стержней АВ и СВ, направленными
вдоль их осей (рис. 1, б), и получаем систему сходящихся сил
(рис. 1, в). Точка В является началом координат. Ось X направляем
перпендикулярно реакции RAB. Составим уравнения равновесия:
. (1)
. (2)
Из уравнения
(1)
Н 
кН.
Из уравнения (2)
Ответ: 
кН; 
кН.
Пример 16. Из-за разной длины стропильных тросов АВ и СВ
равномерный подъем трубы АС весом 3
кН происходит с перекосом, причем трос СВ оказался расположенным горизонтально (рис. 1, а). Определить
силы натяжения стропильных тросов. Указание: центр тяжести трубы лежит на вертикали, проходящей через точку
В.
Рис. 1
Решение. Освобождаем
тело (крюк) от связей (стропильные тросы АВ
и АС), заменяя их
действие на тело реакциями 
и (рис. 1, б).
Рассмотрим равновесие точки В, получим в этой точке плоскую систему трёх сходящихся сил:
, и NСВ и спроецируем
их на оси X и Y (рис. 1, в). Уравнения равновесия будут иметь вид
. (1)
.
(2)
Из уравнения (2)
Н = 6 кН.
Из уравнения
(1)
Н 
кН.
Ответ: 
кН; 
кН.
Пример 17. С помощью
опорного троса АВ и двух
блоков удерживаются в равновесии три груза (рис. 1, а). Определить вес груза 
и силу натяжения опорного троса, если 
= 5 кН и 
= 7 кН. Трением на блоках пренебречь.
Рис. 1
Решение. Рассмотрим
равновесие точки схода В. К ней
приложены силы и , направленные от точки. Освобождаем точку В от связи (трос АВ), при этом реакция NАВ направлена вдоль троса (рис. 1, б). В точке В получим плоскую
систему четырех сходящихся уравновешенных сил: NАВ, , и (рис. 1, в). Точка В является
началом координат. Спроецируем силы на оси X и Y. Составим
уравнения равновесия:
,
откуда
,
откуда
Ответ: 
кН; 
кН.
Пример 18. Тело весом G = 4 Н под
действием горизонтальной силы F равномерно перемещается вверх по наклонной плоскости (рис.
1, а). Приняв силу сопротивления движению (силу
трения) Fтр = 0,13G, определить
значение силы F, а также
нормальную реакцию опорной плоскости.
Рис. 1
Решение. Освобождаем тело от связи (наклонная
плоскость), заменяя её действие на тело реакцией R (рис. 1, б). Рассмотрим равновесие точки М и получим плоскую систему четырех
сходящихся уравновешенных сил: R, F, G и Fтр.
При этом реакция R направлена перпендикулярно
наклонной плоскости. Приняв точку М
за начало координат, перенесём в эту точку силы R, F, G и Fтр и спроецируем
их на оси X и Y (рис. 1,
в). Ось X направим перпендикулярно реакции R. Составим уравнения равновесия:
; (1)
. (2)
Из уравнения
(1)
Н.
Из уравнения (2)
Н.
Ответ: 
Н; 
Н.
Пример 19. Четыре
стержня, приваренные к косынке, образуют узел фермы строительной конструкции (рис.
1, а). Стержень 2 расположен вертикально. Силы в
стержнях 1 и 2 известны и равны
соответственно = 12 кН и = 7 кН. Определить
силы 
и 
в стержнях 3 и 4. Весом частей конструкции
пренебречь.
Рис. 1
Решение. К
косынке приложены четыре активные силы: , , и (рис. 1, б). Рассмотрим равновесие точки А.
Получаем плоскую систему сходящихся уравновешенных сил. Приняв точку А за начало
координат, перенесём в неё силы , , и и спроецируем их на
оси X и Y (рис. 1, в).
Ось X направим вдоль
стержней 1 и 4, которые лежат на одной прямой. Составим уравнения равновесия:
(1)
. (2)
Из уравнения (2)
кН.
Из уравнения
(1)
Ответ: 
кН; 
кН.
Пример 20. Определить по способу вырезания
узлов усилия в стержнях фермы, изображенной на рис. 1.36, а, если к узлу Е фермы приложена вертикальная сила F = 60 кН.
а)
б)
в)
Рис. 1
Решение. Так как сила F = 60 кН, приложенная к узлу Е
фермы, вертикальна и реакция шарнирно-подвижной опоры В, перпендикулярная к опорной
плоскости, тоже вертикальна, то линия действия реакции шарнирно-неподвижной
опоры А должна быть параллельна им,
т. е. тоже должна быть вертикальна. Согласно этому примечанию для трех
параллельных взаимно уравновешивающихся сил RA, RB и F имеем:
кН; 
откуда
кН и 
кН.
Составим по
два уравнения равновесия сил, приложенных к каждому из узлов фермы (рис. 1, б),
и для проверки правильности произведенных вычислений построим многоугольники
сил, которые должны быть замкнутыми. При построении многоугольников все силы
отложим в некотором масштабе по их истинным направлениям, соответствующим
растяжению или сжатию, руководствуясь результатами вычислений (рис. 1, в).
Расчет начнем
с узла А, к
которому приложены лишь две неизвестные силы N1
и N2.
Узел А
кН; 
кН.
Узел С
кН; 
кН.
Узел E
кН; 
кН.
Узел F
кН.
Узел В
кН.
Результаты
расчётов сводим в табл. 1.
Таблица 1. Результаты
расчётов
|
№ стержня |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
N, кН |
-80 |
69,2 |
-40 |
-69,2 |
40 |
34,6 |
0 |
34,6 |
-40 |
Приведенная табл. 1 усилий показывает, что верхний пояс
фермы сжат, нижний -
растянут.
Пример 21. Пример имеет своим прототипом
схему по расчёту усилий в раскосах и поясах мачтовых опор ЛЭП.
Для фермы (рис. 1, а) определить усилия в
стержнях, если в узле Е приложена
сила F = 1800 Н, в узле С – сила 2F, а угол = 37° (sin = 0,6 и cos = 0,8).
Размеры
стержня указаны на чертеже.
Рис.1
Решение. От действия на ферму сил F и 2F
реакции опор соответственно будут RA = 2F и RB = F. Обратимся к определению усилий в стержнях фермы способом
вырезания узлов. Определение усилий начинают с узла, в котором сходятся только
два стержня (узлы A и B). В дальнейшем выбирают такие
узлы фермы, в которых также будут неизвестными два усилия, и так до тех пор,
пока не будут определены усилия во всех стержнях фермы.
Узел А. Вырезав узел (рис. 1, б), приложим к нему неизвестные усилия N1 (в стержне 1), N2 (в
стержне 2) и реакцию опоры в точке А - RA. В итоге на узел подействует плоская система трех сходящихся сил.
Для определения неизвестных усилий N1 и N2 составим уравнения равновесия:
Неизвестные усилия будем всегда
принимать растягивающими - усилия направлены
от узла. Если в результате вычисления усилие окажется отрицательным, то
принятое направление усилия следует заменить на
обратное (сжатие).
Выберем
систему координат через точку А так, чтобы ось Х
совпадала с линией действия усилия N1. В этом
случае уравнения равновесия принимают вид
,
откуда
Н (сжатие).
Знак «минус»
для усилия N2 указывает на то, что
стержень не растянут, а сжат (следует изменить на рис. 1, б направление усилия N2). После этого изменения уравнение åХ = 0 принимает вид 
, откуда 
, или 
Н (растяжение).
Узел С. Вырезав узел (рис. 2, а), приложим
к нему неизвестные усилия N3 (в стержне 3) и N9 (в стержне 9). В итоге в узле С действует плоская система
четырех сходящихся сил, из которых неизвестными усилиями являются N3 и N9. Выбрав
через точку С
систему координат Х и Y, напишем уравнения равновесия: åХ = 0; N3 - N1 = 0, откуда N3 = N1 = 4800 Н (растяжение); åY = 0; N9 - 2F = 0, откуда N9 = 2F = 3600 Н (растяжение).
Узел D. Вырезав узел (рис. 2, б), приложим к нему неизвестные усилия N4 (в стержне 4)
и N10 (в стержне 10).
В итоге в узле D действует плоская система четырех сходящихся сил, из
которых неизвестными являются усилия N4 и N10.
а)
б)
Рис. 2
Выберем через
точку D
систему координат Х и Y так, чтобы ось Х
проходила по стержню 4, уравнения равновесия принимают вид
или
,
или
Н (сжатие).
Направление усилия N10 следует
изменить на обратное (рис. 2, б).
или
,
N4 = -3100
Н (сжатие).
Направление усилия N4 также
следует изменить на обратное (рис. 2, б).
Узел Е. Вырезав узел (рис. 3, а), приложим к нему
неизвестные усилия N6 (в стержне 6) и N11 (в стержне 11). В итоге в узле Е
действует плоская система четырех сходящихся сил: F, N4, N6, N11. Через точку Е проводим систему координат X и Y так, чтобы ось Y проходила по стержню
11. Составляем уравнения равновесия:
откуда
Н (растяжение)
откуда
(сжатие).
Рис. 3
Направление
усилия 
следует направить в
обратную сторону (см. рис. 3, а).
Узел F. Вырезав узел (рис. 3, б), приложим к нему неизвестные усилия 
(в стержне 5) и 
(в стержне 12). В
итоге в узле F получаем плоскую систему пяти сходящихся
сил, из которых неизвестными усилиями являются и . Выбрав через точку F систему координат X и Y, напишем уравнения равновесия:
откуда
Н (сжатие).
Направление усилия N12 следует
изменить на обратное (см. рис. 3, б).
,
откуда
Н (растяжение).
Узел К. Вырезав узел (рис. 4, а), приложим к нему
неизвестные усилия 
(в стержне 8) и 
(в стержне 13). В
итоге в узле F получаем плоскую систему
четырех сходящихся сил: N6, N12, N13 и N8. Через точку К
проводим систему координат X и Y, так, чтобы ось Y проходила по стержню
В. Составляем уравнения равновесия:
откуда
Н (растяжение).
откуда
Н (сжатие).
Рис. 4
Направление усилия N13 следует изменить на обратное (рис. 4, а).
Узел G. Вырезав узел (рис. 4, б), приложим к нему неизвестное усилие 
(в стержне 7). В итоге
в узле G получаем систему трех сходящихся сил с
неизвестным усилием N7. Выбрав через точку G систему координат X и Y, запишем уравнения равновесия:
откуда
Н (растяжение).
Таблица 2. Результаты
расчётов
|
№ стержня |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
N, кH |
4,8 |
6 |
4,8 |
3,1 |
16,96 |
3,1 |
16,96 |
|
№ стержня |
8 |
9 |
10 |
11 |
12 |
13 |
|
|
N, кH |
15,3 |
3,6 |
3 |
5,52 |
12,2 |
14,64 |
|
Пример 22. Применить леммы о нулевых стержнях к
определению незагруженных стержней ферм, изображенных вместе с действующими на
них внешними силами и реакциями опор (рис. 1-5).
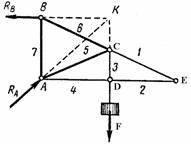
Рис.1 Рис.2
Применяя лемму
2 к узлу D фермы, изображенной на рис. 1,
устанавливаем, что N3 = 0. Мысленно
отбрасывая стержень 3, применяем эту же лемму к узлу C и находим, что N5 = 0.
Рассматривая ферму, изображенную на рис. 2, применяем лемму 1 к узлу E и заключаем, что N1
= 0 и N2 = 0. Затем применяем лемму 3 к узлу D и устанавливаем, что N4 = 0.
На рис. 3
рассматриваем узлы C, D, E и находим: N11 = 0, N9 = 0, N3 =
0. Рассматривая узлы C и D (рис. 4), можно заключить, что N11 =
0 и N9 = 0.
Рис.3 Рис.4
Рассматривая
последовательно узлы C - M фермы, изображенной на рис. 5, находим:
N15 = 0; N13 = 0; N11 = 0; N9 = 0; N7 = 0; N5 = 0; N3 = 0.
Рис.
5
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
