Главная

Лекция 2. Равновесие системы сил. Пара сил.

В данной лекции рассматриваются следующие вопросы

1. Проекция силы на ось и на плоскость.

2. Геометрический способ сложения сил.

3. Равновесие системы сходящихся сил.

4. Момент силы относительно центра или точки.

5. Теорема Вариньона о моменте равнодействующей.

6. Пара сил.

7. Момент пары.

8. Свойства пар.

9. Сложение пар.

10. Теорема о параллельном переносе силы.

11. Приведение плоской системы сил к данному центру.

12. Условия равновесия произвольной плоской системы сил.

13. Случай параллельных сил.

14. Равновесие плоской системы параллельных сил.

15. Сложение параллельных сил. Центр параллельных сил.

16. Понятие о распределенной нагрузке.

17. Расчет составных систем. Статически определимые и статически неопределимые задачи.

18. Графическое определение опорных реакций.

19. Решение задач.

Изучение этих вопросов необходимо в дальнейшем для изучения центра тяжести, произвольной пространственной системы сил, сил трения скольжения, моментов трения качения, решения задач в дисциплине «Сопротивление материалов».

Проекция силы на ось и на плоскость.

Перейдем к рассмотрению аналитического (численного) метода решения задач статики. Этот метод основывается на понятии о проекции силы на ось. Как и для всякого другого вектора, проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак плюс, если перемещение от ее начала к концу происходит в положительном направлении оси, и знак минус - если в отрицательном. Из определения следует, что проекции данной силы на любые параллельные и одинаково направленные оси равны друг другу. Этим удобно пользоваться при вычислении проекции силы на ось, не лежащую в одной плоскости с силой.

Рис. 1

Обозначать проекцию силы на ось Ох будем символом F_x. Тогда для сил, изображенных на рис.1, получим:

Но из чертежа видно, что

Следовательно,

т. е. проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси. При этом проекция будет положительной, если угол между направлением силы и положительным направлением оси - острый, и отрицательной, если этот угол - тупой; если сила перпендикулярна к оси, то ее проекция на ось равна нулю.

Рис.2

Проекцией силы на плоскость Оху называется вектор , заключенный между проекциями начала и конца силы на эту плоскость (рис. 2). Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только своим численным значением, но и направлением в плоскости Оху. По модулю , где — угол между направлением силы и ее проекции .

В некоторых случаях для нахождения проекции силы на ось бывает удобнее найти сначала ее проекцию на плоскость, в которой эта ось лежит, а затем найденную проекцию на плоскость спроектировать на данную ось.

Например, в случае, изображенном на рис. 2, найдем таким способом, что

Геометрический способ сложения сил.

Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил. Величину, равную геометрической сумме сил какой-нибудь системы, будем называть главным вектором этой системы сил. Понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей, для многих систем сил, как мы увидим в дальнейшем, равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил.

Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил (рис. 3, a), откладываем от произвольной точки О (рис. 3, б) вектор Oa, изображающий в выбранном масштабе cилу F₁, от точки a откладываем вектор , изображающий силу F₂, от точки b откладываем вектор bc, изображающий силу F₃ и т. д.; от конца m предпоследнего вектора откладываем вектор mn, изображающий силу F_n. Соединяя начало первого вектора с концом последнего, получаем вектор , изображающий геометрическую сумму или главный вектор слагаемых сил:

или

От порядка, в котором будут откладываться векторы сил, модуль и направление не зависят. Легко видеть, что проделанное построение представляет собою результат последовательного применения правила силового треугольника.

Рис.3

Фигура, построенная на рис. 3,б, называется силовым (в общем случае векторным) многоугольником. Таким образом, геометрическая сумма или главный вектор нескольких сил изображается замыкающей стороной силового многоугольника, построенного из этих сил (правило силового многоугольника). При построении векторного многоугольника следует помнить, что у всех слагаемых векторов стрелки должны быть направлены в одну сторону (по обводу многоугольника), а у вектора - в сторону противоположную.

Равнодействующая сходящихся сил. При изучении статики мы будем последовательно переходить от рассмотрения более простых систем сил к более сложным. Начнем с рассмотрения системы сходящихся сил.

Сходящимися называются силы, линии действия которых пересекаются в одной точке, называемой центром системы (см. рис. 3, а).

По следствию из первых двух аксиом статики система сходящихся сил, действующих на абсолютно твердое тело, эквивалентна системе сил, приложенных в одной точке (на рис. 3, а в точке А).

Последовательно применяя аксиому параллелограмма сил, приходим к выводу, что система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке их пересечения. Следовательно, если силы сходятся в точке A (рис. 3, а), то сила, равная главному вектору , найденному построением силового многоугольника, и приложенная в точке А, будет равнодействующей этой системы сил.

Примечания.

1. Результат графического определения равнодействующей не изменится, если силы суммировать в другой последовательности, хотя при этом мы получим другой силовой многоугольник - отличный от первого.

2. Фактически силовой многоугольник, составленный из векторов сил заданной системы, является ломаной линией, а не многоугольником в привычном смысле этого слова.

3. Отметим, что в общем случае этот многоугольник будет пространственной фигурой, поэтому графический метод определения равнодействующей удобен только для плоской системы сил.

Равновесие системы сходящихся сил.

Из законов механики следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, которое мы назовем движением «по инерции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела.

Отсюда получаем два важных вывода:

1) Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции».

2) Уравновешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела; в покое тело будет при этом находиться лишь в том случае, если оно было в покое и до момента приложения к нему уравновешенных сил.

Для равновесия приложенной к твердому телу системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или аналитической форме.

1. Геометрическое условие равновесия. Так как равнодействующая сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то может обратиться в нуль тогда и только тогда, когда конец последней силы в многоугольнике совпадает с началом первой, т. е. когда многоугольник замкнется.

Следовательно, для равновесия системы, сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут.

2. Аналитические условия равновесия. Аналитически равнодействующая системы сходящихся сил определяется формулой

.

Так как под корнем стоит сумма положительных слагаемых, то R обратится в нуль только тогда, когда одновременно , т. е. когда действующие на тело силы будут удовлетворять равенствам:

Равенства выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.

Если все действующие на тело сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил. В случае плоской системы сходящихся сил получим, очевидно, только два условия равновесия

Равенства выражают также необходимые условия (или уравнения) равновесия свободного твердого тела, находящегося под действием сходящихся сил.

Теорема о трех силах. Уравновешенная плоская система трех непараллельных сил является сходящейся.

Условие «плоская» в формулировке теоремы не является необходимым - можно убедиться, что любая уравновешенная система трех сил всегда будет плоской. Это следует из условий равновесия произвольной пространственной системы сил, которые будут рассмотрены далее.

Пример 1. На рис.4 показаны три силы. Проекции сил на оси х, у, z очевидны:

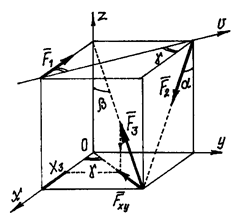
Рис.4

Рис. 2.4.

А чтобы найти проекцию силы на ось х нужно использовать правило двойного проектирования.

Проектируем силу сначала на плоскость хОу, в которой расположена ось (рис.4), получим вектор , величиной а затем его проектируем на ось х: .

Аналогично действуя, найдём проекцию на ось у: .

Проекция на ось z находится проще: .

Нетрудно убедиться, что проекции сил на ось V равны:

;

При определении этих проекций удобно воспользоваться рис.5, видом сверху на расположение сил и осей.

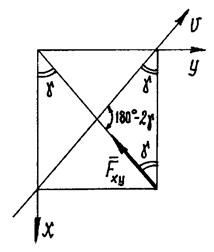
Рис.5

Вернёмся к системе сходящихся сил (рис. 6). Проведём оси координат с началом в точке пересечения линий действия сил, в точке О.

Мы уже знаем, что равнодействующая сил . Спроектируем это векторное равенство на оси. Получим проекции равнодействующей на оси x, y, z:

Они равны алгебраическим суммам проекций сил на соответствующие оси. А зная проекции равнодействующей, можно определить и величину её как диагональ прямоугольного параллелепипеда или

.

Направление вектора найдём с помощью направляющих косинусов (рис.6):

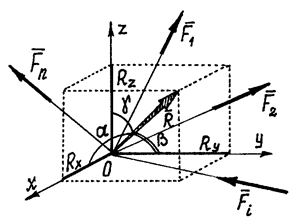
Рис.6

Пример 2. На шар, вес которого Р, лежащий на горизонтальной плоскости и привязанный к ней нитью АВ, действует сила F (рис.7). Определим реакции связей.

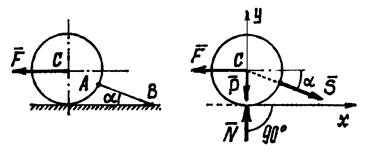
Рис.7

Следует сразу заметить, что все задачи статики решаются по одной схеме, в определённом порядке.

Продемонстрируем ее на примере решения этой задачи.

1. Надо выбрать (назначить) объект равновесия – тело, равновесие которого следует рассмотреть, чтобы найти неизвестные.

В этой задаче, конечно, объект равновесия – шар.

2. Построение расчётной схемы. Расчётная схема – это объект равновесия, изображённый отдельно, свободным телом, без связей, со всеми силами, действующими на него: реакциями и остальными силами.

Показываем реакцию нити и нормальную реакцию плоскости – (рис.7). Кроме них на шар действуют заданные силы и .

3. Надо установить какая получилась система сил и составить соответствующие уравнения равновесия.

Здесь получилась система сходящихся сил, расположенных в плоскости, для которой составляем два уравнения (оси можно проводить произвольно):

4. Решаем систему уравнений и находим неизвестные.

По условию задачи требовалось найти давление шара на плоскость. А мы нашли реакцию плоскости на шар. Но, по определению следует, что эти силы равны по величине, только давление на плоскость будет направлено в противоположную сторону, вниз.

Пример 3. Тело весом Р прикреплено к вертикальной плоскости тремя стержнями (рис.8). Определим усилия в стержнях.

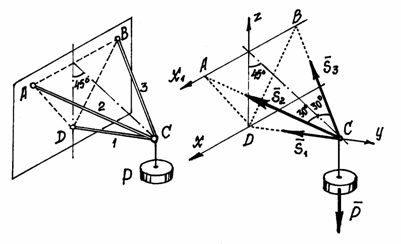
Рис.8

В этой задаче объект равновесия – узел С вместе с грузом. Он нарисован отдельно с реакциями, усилиями в стержнях и весом . Силы образуют пространственную систему сходящихся сил. Составляем три уравнения равновесия:

Из первого уравнения следует: S₂ = S₃. Тогда из третьего:

, а из второго:

Когда мы направляли усилие в стержне от узла, от объекта равновесия, предполагали, что стержни работают на растяжение. Усилие в стержне CD получилось отрицательным. Это значит – стержень сжат. Так что знак усилия в стержне указывает как работает стержень: на растяжение или на сжатие.

Пример 4. Определить реакции стержней, соединенных шарниром В, если к нему подвешен груз весом Q (рис.9,а).

Решение. В соответствии с предложенным выше планом выбираем тело, равновесие которого мы будем рассматривать. Этот выбор, в основном, определяется условиями задачи. Если в этой задаче рассмотреть равновесие подвешенного груза, то мы сумеем найти только силу натяжения нити, которая равна весу тела: T = Q (рис.9,б).

Чтобы определить реакции стержней, рассмотрим равновесие точки В. Можно считать, что к ней посредством нити приложена активная сила Q и реакции отброшенных стержней S_A и S_C (рис.9,в).

Решим эту задачу аналитически. Выбирая начало отсчета в точке В, составим уравнения равновесия, которые примут вид:

-S_A cosα + S_C cosβ = 0;

S_A sinα + S_C sinβ = Q.

Чтобы найти отсюда S_C сложим полученные уравнения, умножив предварительно первое из них на sinα, а второе – на cosα:

S_C (sinαcosβ + cosα sinβ) = Q cosα.

Отсюда следует, что S_C = Q cosα/sin(α+β), а поскольку α и β в эти уравнения входят симметрично, то S_A = Q cosβ/sin(α+β).

Для проверки правильности аналитического решения задачи воспользуемся графическим методом.

Треугольник, образованный из трех сил: Q, S_A и S_C должен быть замкнут, поэтому решение сводится к построению треугольника по известной стороне (Q) и направлению двух других сторон (S_A и S_C). Для этого нужно в масштабе построить вектор Q, а затем из начала и из конца этого вектора провести прямые, параллельные S_A и S_C до их пересечения (рис.9,г).

Измерив длины найденных отрезков и пересчитав в масштабе, можно считать поставленную задачу решенной. Направление полученных векторов определяется из условия замкнутости силового многоугольника, то есть конец последнего вектора должен совпадать с началом первого.

Рис.9

Можно, впрочем, определить величину S_A и S_C и без масштабной линейки, если просто решить построенный треугольник.

С этой целью воспользуемся теоремой синусов:

откуда, заменяя синус дополнительного угла косинусом, получим:

То есть, результат графического решения совпадает с аналитическим, значит задача решена правильно.

Пример 5. Центр невесомого идеального блока удерживается при помощи двух стержней, соединенных шарнирно в точке В. Через блок переброшена нить, один конец которой закреплен, а к другому – подвешен груз весом Q (рис.10,а). Определить реакции стержней, пренебрегая размерами блока.

Решение. Рассмотрим равновесие блока В, к которому приложены силы натяжения нитей Т₁ и Т₂ и реакции отброшенных стержней S_A и S_С, которые, как и в предыдущем примере мы считаем растянутыми (рис.10,б).

Фактически в качестве активной силы выступает вес груза Q, который приложен к блоку с помощью нити, поэтому Т₁ = Q. По поводу силы Т₂ надо отметить, что идеальным – то есть без трения блоком называется механизм, который меняет направление силы натяжения нити, но не ее величину, поэтому Т₁ = Т₂ = Q.

Пренебрегая размерами блока, получим уравновешенную систему сходящихся сил, приложенных в точке В (рис.10,в).

Определим реакции S_A и S_С аналитически. Отметим, что если в первое из аналитических уравнений равновесия входят оба неизвестных, то в уравнение ΣY_i = 0 неизвестная реакция S_С не войдет, поэтому имеет смысл начать решение задачи именно с этого уравнения:

S_Acos30°+ Т₂ cos60°- Т₁ = 0.

Подставляя сюда значения тригонометрических функций и Т₁ = Т₂ = Q, получим:

Откуда

Теперь вернемся к уравнению ΣX_i = 0:

- S_Acos60°+ Т₂ cos30°+ S_С = 0,

или

Подставив найденное выше значение S_A, получим:

При этом минус в последнем выражении означает, что стержень ВС не растянут, как мы предполагали, а сжат.

Для проверки полученного результата решим эту задачу графически. С этой целью от центра О последовательно откладываем в масштабе известные силы Т₁ и Т₂, затем от начала первого и от конца последнего вектора проводим прямые, параллельные S_A и S_С до их пересечения (рис.10,г).

Рис.10

Нетрудно видеть, что построенный силовой многоугольник имеет ось симметрии и |S_A|=|S_С|. При этом направление вектора S_С на силовом многоугольнике противоположно первоначальному направлению, указанному на чертеже, то есть стержень ВС не растянут, а сжат.

Примечания.

1. В системе аналитических уравнений равновесия оси координат не обязательно должны быть взаимно перпендикулярными, поэтому, если в последнем примере выбрать ось Ох, совпадающую по направлению с силой Т₂ , мы получим систему уравнений, из которых неизвестные S_A и S_С находятся независимо одно от другого.

2. Впоследствии мы увидим, что аналитическое решение можно проверить не только с помощью графического решения, но и аналитически. Впрочем, для системы сходящихся сил изложенный метод решения задач является, по-видимому, оптимальным.

Момент силы относительно центра (или точки).

Опыт показывает, что под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется ее моментом.

Рассмотрим силу , приложенную в точке А твердого тела (рис. 11). Допустим, что сила стремится повернуть тело вокруг центра О. Перпендикуляр h, опущенный из центра O на линию действия силы , называется плечом силы относительно центра О. Так как точку приложения силы можно произвольно перемещать вдоль линии действия, то, очевидно, вращательный эффект силы будет зависеть: 1) от модуля силы F и длины плеча h; 2) от положения плоскости поворота ОАВ, проходящей через центр О и силу F; 3) от направления поворота к этой плоскости.

Рис.11

Ограничимся пока рассмотрением систем сил, лежащих в одной плоскости. В этом случае плоскость поворота для всех сил является общей и в дополнительном задании не нуждается.

Тогда для количественного измерения вращательного эффекта можно ввести следующее понятие о моменте силы: моментом силы относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.

Момент силы относительно центра О будем обозначать символом m₀(F). Следовательно,

В дальнейшем условимся считать, что момент имеет знак плюс, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки, и знак минус, - если по ходу часовой стрелки. Так, для силы , изображенной на рис.20,а, момент относительно центра О имеет знак плюс, а для силы, показанной на рис.20,б, - знак минус.

Отметим следующие свойства момента силы:

1) Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия.

2) Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю).

3) Момент силы численно выражается удвоенной площадью треугольника ОАВ (рис. 20,б)

Этот результат следует из того, что

Рассмотренное определение момента силы подходит только для плоской системы сил.

Теорема Вариньона о моменте равнодействующей.

Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.

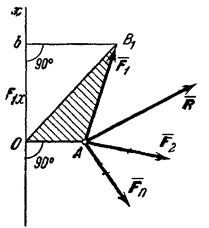
Рис.12

Рассмотрим систему сил , сходящихся в точке А (рис.12). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.

Для доказательства теоремы найдем соответствующие выражения моментов m₀(), m₀(), … . По формуле . Но, как видно из рисунка, где F_1x - проекция силы на ось Ох; следовательно

.

Аналогично вычисляются моменты всех других сил.

Обозначим равнодействующую сил , через , где . Тогда, по теореме о проекции суммы сил на ось, получим . Умножая обе части этого равенства на ОА, найдем:

или,

.

Пара сил. Момент пары.

Парой сил (или просто парой) называются две силы, равные по величине, параллельные и направленные в противоположные стороны (рис.13). Очевидно, и .

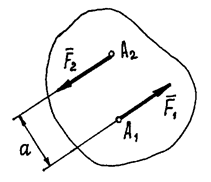
Рис.13

Несмотря на то, что сумма сил равна нулю, эти силы не уравновешиваются. Под действием этих сил, пары сил, тело начнёт вращаться. И вращательный эффект будет определяться моментом пары:

.

Расстояние a между линиями действия сил называется плечом пары.

Если пара вращает тело против часовой стрелки, момент её считается положительным (как на рис.13), если по часовой стрелке – отрицательным.

Для того, чтобы момент пары указывал и плоскость, в которой происходит вращение, его представляют вектором.

Вектор момента пары направляется перпендикулярно плоскости, в которой расположена пара, в такую сторону, что если посмотреть оттуда, увидим вращение тела против часовой стрелки (рис. 14).

Нетрудно доказать, что вектор момента пары – есть вектор этого векторного произведения (рис. 14). И заметим, что он равен вектору момента силы относительно точки А, точки приложения второй силы:

.

О точке приложения вектора будет сказано ниже. Пока приложим его к точке А.

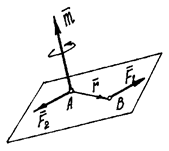
Рис.14

Свойства пар

1) Проекция пары на любую ось равна нулю. Это следует из определения пары сил.

2) Найдём сумму моментов сил оставляющих пару, относительно какой-либо точки О (рис.15).

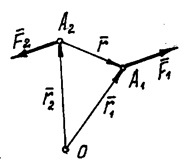
Рис.15

Покажем радиусы-векторы точек А₁ и А₂ и вектор , соединяющий эти точки. Тогда момент пары сил относительно точки О

.

Но . Поэтому .

Но .

Значит .

Момент пары сил относительно любой точки равен моменту этой пары.

Отсюда следует, что, во-первых, где бы не находилась точка О и, во-вторых, где бы не располагалась эта пара в теле и как бы она не была повёрнута в своей плоскости, действие её на тело будет одинаково. Так как момент сил, составляющих пару, в этих случаях один и тот же, равный моменту этой пары .

Поэтому можно сформулировать ещё два свойства.

3) Пару можно перемещать в пределах тела по плоскости действия и переносить в любую другую параллельную плоскость.

4) Так как действие на тело сил, составляющих пару, определяется лишь её моментом, произведением одной из сил на плечо, то у пары можно изменять силы и плечо, но так, чтобы момент пары остался прежним. Например, при силах F₁=F₂=5 H и плече а = 4 см момент пары m = 20 H∙см. Можно силы сделать равными 2 Н, а плечо а = 10 см. При этом момент останется прежним 20 Нсм и действие пары на тело не изменится.

Все эти свойства можно объединить и, как следствие, сделать вывод, что пары с одинаковым вектором момента и неважно где расположенные на теле, оказывают на него равное действие. То есть такие пары эквивалентны.

Исходя из этого, на расчётных схемах пару изображают в виде дуги со стрелкой, указывающей направление вращения, и рядом пишут величину момента m (рис.15.1). Или, если это пространственная конструкция, показывают только вектор момента этой пары. И вектор момента пары можно прикладывать к любой точке тела. Значит вектор момента пары – свободный вектор. Такое упрощенное изображение оправдано тем, что пара сил характеризуется моментом, а не ее положением в плоскости. Но если необходимо определять не внешние силы, а внутренние в разных сечениях элемента, как это делается в сопротивлении материалов, то важен знак и место приложения пары сил.

Рис.15.1. Эквивалентные пары сил

И ещё одно дополнительное замечание. Так как момент пары равен вектору момента одной из сил её относительно точки приложения второй силы, то момент пары сил относительно какой-либо оси z – есть проекция вектора момента пары на эту ось:

,

где – угол между вектором и осью z.

Сложение пар.

Пусть даны две пары с моментами m₁ и m₂, расположенные в пересекающихся плоскостях (рис.16).

Сделаем у пар плечи одинаковыми, равными а = АВ. Тогда модули сил, образующих первую пару, должны быть равны: , а образующих вторую пару: .

Эти пары показаны на рис.16, где . И расположены они в своих плоскостях так, что плечи пар совпадают с прямой АВ на линии пересечения плоскостей.

Рис.16

Рис. 4.4.

Сложив силы, приложенные к точкам А и В, построением параллелограммов, получим их равнодействующие . Так как , то эти силы и будут образовывать пару, момент которой , где – радиус-вектор точки В, совпадающий с АВ.

Так как , то момент полученной пары

.

Следовательно, в результате сложения пар, расположенных в пересекающихся плоскостях, получится пара сил. Момент её будет равен векторной сумме моментов слагаемых пар.

При сложении нескольких пар, действующих в произвольных плоскостях, получим пару с моментом

.

Конечно, эта результирующая пара будет располагаться в плоскости перпендикулярной вектору .

Равенство нулю результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие равновесия пар

=0.

Это является необходимым и достаточным условием равновесия систем пар.

Если пары расположены в одной плоскости, векторы моментов их будут параллельны. И момент результирующей пары можно определить как алгебраическую сумму моментов пар.

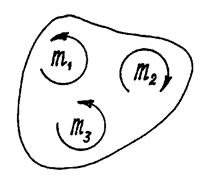
Рис.17

Например, пары, показанные на рис.17, расположены в одной плоскости и моменты их:

m₁=2 Hсм , m₂=5 Hсм, m₃=3 Hсм. Пары уравновешиваются, потому что алгебраическая сумма их моментов равна нулю:

Пример 6. Определить опорные реакции рамы, загруженной системой пар (рис.18).

Рис.18

Решение. Заменим систему пар, приложенных к раме, результирующей парой по формуле:

M_R = M₁ - M₂ + M₃ = 3 - 4 + 7 = 6 кНм.

Из условия равновесия систем пар =0 следует, что активную пару M_R , приложенную к раме, может уравновесить только пара сил, образованных опорными реакциями, поэтому линия действия R_A должна быть параллельной R_В и

M_R + M (R_A, R_В) = 0,

откуда R_A = R_В = M_R /d , где d = 6cos30°= 3 м - плечо пары (R_A, R_В).

Итак, R_A = R_В = 6/(3) = (2)/3 м.

Теорема о параллельном переносе силы.

Одной из основных задач, решаемых статикой, является замена одной системы сил другой – эквивалентной ей.

Такая процедура позволяет все многообразие систем сил свести к простейшим каноническим системам, классифицировать их и получить уравнения равновесия, необходимые для решения практических задач. Ключевую роль в проведении таких преобразований систем сил играет следующая теорема, называемая Лемма Пуансо.

Равнодействующая системы сходящихся сил непосредственно находится с помощью аксиомы параллелограмма сил. Для двух параллельных сил эта задача была решена путем приведения их к сходящимся силам. Очевидно, что аналогичную задачу легко будет решить и для произвольной системы сил, если найти и для них метод приведения к силам, приложенным в одной точке.

Ранее мы установили, что вектор силы можно переносить по линии действия в любую точку тела.

Попробуем силу (рис. 19) перенести в какую-нибудь точку О, не расположенную на линии действия.

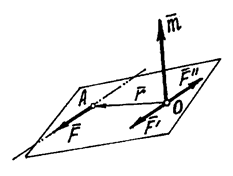
Рис.19

Приложим к этой точке две уравновешивающиеся силы и , параллельные силе и равные ей по величине:

В результате получим силу , приложенную к точке О. То есть мы как бы перенесли заданную силу из точки А в точку О, но при этом появилась пара, образованная силами и . Момент этой пары , равен моменту заданной силы относительно точки О.

Этот процесс замены силы равной ей силой и парой называется приведением силы к точке О.

Точка О называется точкой приведения; сила , приложенная к точке приведения, – приведённой силой. Появившаяся пара – присоединённой парой.

Приведение плоской системы сил к данному центру.

Пусть на твердое тело действует какая-нибудь система сил , лежащих в одной плоскости. Возьмем в этой плоскости произвольную точку О, которую назовем центром приведения, и, перенесем все силы в центр О (рис. 20, а). В результате на тело будет действовать система сил приложенных в центре О, и система пар, моменты которых будут равны:

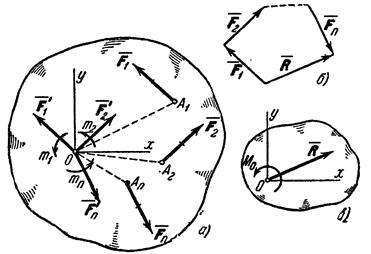
Рис.20

Силы, приложенные в центре О, можно заменить одной силой , приложенной в том же центре; при этом или

Точно так же, по теореме о сложении пар, все пары можно заменить одной парой, лежащей в той же плоскости. Момент этой пары или .

Величина , равная геометрической сумме всех сил системы, называется, как известно, главным вектором системы; величину М_о, равную сумме моментов всех сил системы относительно центра О, будем называть главным моментом системы относительно центра О.

В результате мы доказали следующую теорему: всякая плоская система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяется одной силой R, равной главному вектору системы и приложенной в центре приведения О, и одной парой с моментом М₀, равным главному моменту системы относительно центра О (рис. 20, в).

Примечания:

1. Для плоской системы сил под главным моментом системы часто также понимают величину этого момента.

2. Очевидно, что главный вектор R₀ не зависит, а главный момент M₀ зависит от выбора центра приведения.

Частные случаи приведения плоской системы сил.

В зависимости от значений главного вектора R₀ и главного момента M₀ возможны следующие случаи приведения плоской системы сил.

1) R₀ =0, M₀ =0 - система сил находится в равновесии;

2) R₀ =0, M₀ ≠0 - система эквивалентна паре сил с моментом, равным главному моменту системы, который в этом случае не зависит от выбора центра приведения;

3) R₀ ≠0, M₀ =0 - система эквивалентна равнодействующей R, равной и эквивалентной главному вектору системы R₀ , линия действия которой проходит через центр приведения: R = R₀ , R~R₀ ;

4) R₀ ≠ 0, M₀ ≠0 - система эквивалентна равнодействующей R, равной главному вектору системы R₀, ее линия действия проходит на расстоянии d = |M₀|/ R₀ от центра приведения (рис.20, б).

Условия равновесия произвольной плоской системы сил.

Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия: R = 0, M₀ = 0.

Здесь О - любая точка плоскости.

Из этого условия следуют уравнения равновесия произвольной плоской системы сил, которые можно записать в трех различных формах:

1) Первая форма:

ΣM_A = 0;

ΣX = 0;

ΣY = 0.

2) Вторая форма:

ΣM_A = 0;

ΣM_B = 0;

ΣY = 0, где ось Oy неперпендикулярна отрезку АВ.

3) Третья форма:

ΣM_A = 0;

ΣM_B = 0;

ΣM_С = 0, где точки А, В и С не лежат на одной прямой.

Равенства выражают, следующие аналитические условия равновесия: для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.

Теорема о трех моментах. Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.

.

Равновесие плоской системы параллельных сил.

В случае, когда все действующие на тело силы параллельны друг другу, мы можем направить ось Ох перпендикулярно к силам, а ось Оу параллельно им (рис. 21). Тогда проекция каждой из сил на Ox будет равна нулю и первое из 3-х равенств обратится в тождество вида 0 = 0. В результате для параллельных сил останется два условия равновесия:

Где ось Оу параллельна силам.

Рис.21

Сложение параллельных сил. Центр параллельных сил.

Пусть даны две параллельные силы и , направленные в одну сторону и приложенные к точкам и (рис.22).

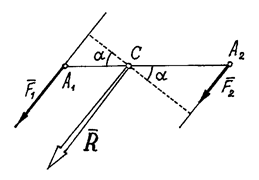
Рис.22

Конечно, величина их равнодействующей . Вектор её параллелен силам и направлен в ту же сторону. С помощью теоремы Вариньона найдём точку приложения равнодействующей – точку С. По этой теореме .

Значит

Отсюда . То есть точка приложения равнодействующей делит расстояние между точками A₁ и A₂ на части обратно пропорциональные силам.

Если параллельные силы направлены в противоположные стороны (рис.23), то аналогично можно доказать, что равнодействующая по величине будет равна разности сил: (если ), параллельна им, направлена в сторону большей силы и расположена за большей силой – в точке С. А расстояния от точки С до точек приложения сил обратно пропорциональны силам:

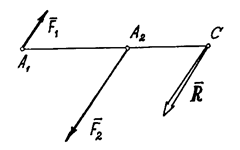
Рис.23

Следует заметить, что если точка приложения равнодействующей расположена на одной прямой с точками A₁ и A₂, точками приложения сил, то, при повороте этих сил в одну сторону на одинаковый угол, равнодействующая также повернётся вокруг точки приложения С в том же направлении, и останется параллельной им.

Такая точка приложения равнодействующей называется центром параллельных сил.

Конечно, если хотя бы одну из сил перенести по своей линии действия в другую точку, то и точка приложения равнодействующей, центр параллельных сил, тоже переместится по линии действия.

Следовательно, положение центра параллельных сил зависит от координат точек приложения сил.

Центром нескольких параллельных сил, найденный последовательным сложением каждых двух сил, будем называть точку С, радиус-вектор которой определяется формулой

, (1)

где - радиусы-векторы точек приложения сил; – величина равнодействующей параллельных сил, равная алгебраической сумме этих сил (знак силы определяется направлением, которое заранее выбирается и считается положительным).

Используя (1), нетрудно найти координаты центра параллельных сил. Если радиусы-векторы откладывать из начала координат, то проекции радиусов-векторов точек на оси будут равны их координатам. Поэтому, проектируя векторное равенство (1) на оси, получим

где – координаты точек приложения сил.

Понятие о распределенной нагрузке.

Наряду с рассмотренными выше сосредоточенными силами строительные конструкции и сооружения могут подвергаться воздействию распределенных нагрузок – по объему, по поверхности или вдоль некоторой линии – и определяемых ее интенсивностью.

Примером нагрузки, распределенной по площади, является снеговая нагрузка, давление ветра, жидкости или грунта. Интенсивность такой поверхностной нагрузки имеет размерность давления и измеряется в кН/м² или килопаскалях (кПа = кН/м²).

При решении задач очень часто встречается нагрузка, распределенная по длине балки. Интенсивность q такой нагрузки измеряется в кН/м.

Рассмотрим балку, загруженную на участке [a, b] распределенной нагрузкой, интенсивность которой изменяется по закону q= q(x). Для определения опорных реакций такой балки нужно заменить распределенную нагрузку эквивалентной сосредоточенной. Это можно сделать по следующему правилу:

Рассмотрим частные случаи распределенной нагрузки.

а) общий случай распределенной нагрузки (рис.24)

Рис.24

q(x) - интенсивность распределенной силы [Н/м],

- элементарная сила.

l – длина отрезка

Распределенная по отрезку прямой сила интенсивности q(x) эквивалентна сосредоточенной силе

Сосредоточенная сила прикладывается в точке С (центре параллельных сил) с координатой

б) постоянная интенсивность распределенной нагрузки (рис.25)

Рис.25

в) интенсивность распределенной нагрузки, меняющаяся по линейному закону (рис.26)

Рис.26

Расчет составных систем.

Под составными системами будем понимать конструкции, состоящие из нескольких тел, соединенных друг с другом.

Прежде, чем переходить к рассмотрению особенностей расчета таких систем, введем следующее определение.

Статически определимыми называются такие задачи и системы статики, для которых число неизвестных реакций связей не превышает максимально допустимого числа уравнений.

Если число неизвестных больше числа уравнений, соответствующие задачи и системы называются статически неопределимыми. При этом разность между числом неизвестных и числом уравнений называется степенью статической неопределимости системы.

Для любой плоской системы сил, действующих на твердое тело, имеется три независимых условия равновесия. Следовательно, для любой плоской системы сил из условий равновесия можно найти не более трех неизвестных реакций связи.

В случае пространственной системы сил, действующих на твердое тело, имеется шесть независимых условия равновесия. Следовательно, для любой пространственной системы сил из условий равновесия можно найти не более шести неизвестных реакций связи.

Поясним это на следующих примерах.

1. Пусть центр невесомого идеального блока (пример 4) удерживается при помощи не двух, а трех стержней: АВ, ВС и BD и нужно определить реакции стержней, пренебрегая размерами блока.

С учетом условий задачи мы получим систему сходящихся сил, где для определения трех неизвестных: S_A, S_C и S_D можно составить по-прежнему систему только двух уравнений: ΣX = 0, ΣY=0. Очевидно, поставленная задача и соответствующая ей система будут статически неопределимыми.

2. Балка, жестко защемленная на левом конце и имеющая на правом конце шарнирно-неподвижную опору, загружена произвольной плоской системой сил (рис.27).

Для определения опорных реакций можно составить только три уравнения равновесия, куда войдут 5 неизвестных опорных реакций: X_A, Y_A, M_A, X_B и Y_B. Поставленная задача будет дважды статически неопределимой.

Такую задачу нельзя решить в рамках теоретической механики, предполагая рассматриваемое тело абсолютно твердым.

Рис.27

Вернемся к изучению составных систем, типичным представителем которых является трехшарнирная рама (рис. 28,а). Она состоит из двух тел: AC и BC, соединенным ключевым шарниром C. На примере этой рамы рассмотрим два способа определения опорных реакций составных систем.

1 способ. Рассмотрим тело AC, загруженное заданной силой Р, отбросив в соответствии с аксиомой 7 все связи и заменив их соответственно реакциями внешних (X_A, Y_A) и внутренних (X_C, Y_C) связей (рис. 28,б).

Аналогично можно рассмотреть равновесие тела BC под действием реакций опоры В - (X_B, Y_B) и реакций в соединительном шарнире C - (X_C’, Y_C’) , где в соответствии с аксиомой 5: X_C = X_C’, Y_C = Y_C’.

Для каждого из этих тел можно составить три уравнения равновесия, таким образом, общее число неизвестных: X_A, Y_A , X_C =X_C’, Y_C =Y_C’, X_B , Y_B равняется суммарному числу уравнений, и задача является статически определимой.

Напомним, что по условию задачи требовалось определить только 4 опорные реакции, нам же пришлось проделать дополнительную работу, определяя реакции в соединительном шарнире. В этом и заключается недостаток данного способа определения опорных реакций.

2 способ. Рассмотрим равновесие всей рамы АВС, отбросив только внешние связи и заменив их неизвестными опорными реакциями X_A, Y_A, X_B , Y_B .

Полученная система состоит из двух тел и не является абсолютно твердым телом, поскольку расстояние между точками А и В может изменяться вследствие взаимного поворота обеих частей относительно шарнира С. Тем не менее можно считать, что совокупность сил, приложенных к раме АВС образует систему, если воспользоваться аксиомой отвердевания (рис.28,в).

Рис.28

Итак, для тела АВС можно составить три уравнения равновесия. Например:

ΣM_A = 0;

ΣX = 0;

ΣY = 0.

В эти три уравнения войдут 4 неизвестных опорных реакции X_A, Y_A, X_B и Y_B . Отметим, что попытка использовать в качестве недостающего уравнения, например такое: ΣM_В = 0 к успеху не приведет, поскольку это уравнение будет линейно зависимым с предыдущими. Для получения линейно независимого четвертого уравнения необходимо рассмотреть равновесие другого тела. В качестве него можно взять одну из частей рамы, например - ВС. При этом нужно составить такое уравнение, которое содержало бы «старые» неизвестные X_A, Y_A, X_B , Y_B и не содержало новых. Например, уравнение: ΣX^(ВС) = 0 или подробнее: -X_С’ + X_B = 0 для этих целей не подходит, поскольку содержит «новое» неизвестное X_С’, а вот уравнение ΣM_С^(ВС) = 0 отвечает всем необходимым условиям. Таким образом, искомые опорные реакции можно найти в следующей последовательности:

ΣM_A = 0; → Y_B = Р/4;

ΣM_В = 0; → Y_А = -Р/4;

ΣM_С^(ВС) = 0; → X_B = -Р/4;

ΣX = 0; → X_А = -3Р/4.

Для проверки можно использовать уравнение: ΣM_С^(АС) = 0 или, подробнее: -Y_А∙2 + X_А∙2 + Р∙1 = Р/4∙2 -3Р/4∙2 + Р∙1 = Р/2 - 3Р/2 + Р = 0.

Отметим, что в это уравнение входят все 4 найденные опорные реакции: X_А и Y_А - в явной форме, а X_B и Y_B - в неявной, поскольку они были использованы при определении двух первых реакций.

Графическое определение опорных реакций.

Во многих случаях решение задач можно упростить, если вместо уравнений равновесия или в дополнение к ним непосредственно использовать условия равновесия, аксиомы и теоремы статики. Соответствующий подход и получил название графического определения опорных реакций.

Прежде чем перейти к рассмотрению графического метода отметим, что, как и для системы сходящихся сил, графически можно решить только те задачи, которые допускают аналитическое решение. При этом графический метод определения опорных реакций удобен при небольшом числе нагрузок.

Итак, графический метод определения опорных реакций основан главным образом на использовании:

- аксиомы о равновесии системы двух сил;

- аксиомы о действии и противодействии;

- теоремы о трех силах;

- условия равновесия плоской системы сил.

При графическом определении реакций составных систем рекомендуется следующая последовательность рассмотрения:

- выбрать тело с минимальным числом алгебраических неизвестных реакций связей;

- если таких тел два или больше, то начать решение с рассмотрения тела, к которому приложено меньшее число сил;

- если таких тел два или больше, то выбрать тело, для которого большее число сил известно по направлению.

Решение задач.

При решения задач этого раздела следует иметь в виду все те общие указания, которые были сделаны ранее.

Приступая к решению, надо, прежде всего, установить, равновесие какого именно тела следует в данной задаче рассмотреть. Затем, выделив это тело и рассматривая его как свободное, следует изобразить все действующие на тело заданные силы и реакции отброшенных связей.

Далее следует составить условия равновесия, применяя ту из форм этих условий, которая приводит к более простой системе уравнений (наиболее простой будет система уравнений, в каждое из которых входит по одному неизвестному).

Для получения более простых уравнений следует (если это только не усложняет ход расчета):

1) составляя уравнения проекций, проводить координатную ось, перпендикулярно какой-нибудь неизвестной силе;

2) при составлении моментного уравнения в качестве моментной целесообразно выбирать точку, где пересекаются линии действия двух неизвестных опорных реакций из трех – в этом случае они не войдут в уравнение, и оно будет содержать только одно неизвестное;

3) если две неизвестных опорных реакции из трех параллельны, то при составлении уравнения в проекциях на ось последнюю следует направить так, чтобы она была перпендикулярна к двум первым реакциям – в этом случае уравнение будет содержать только последнее неизвестное;

4) при решении задачи систему координат надо выбирать так, чтобы ее оси были ориентированы так же, как большинство приложенных к телу сил системы.

При вычислении моментов иногда бывает удобно разлагать данную силу на две составляющие и, пользуясь теоремой Вариньона, находить момент силы как сумму моментов этих составляющих.

Решение многих задач статики сводится к определению реакций опор, с помощью которых закрепляются балки, мостовые фермы и т. п.

Пример 7. К кронштейну, изображенному на рис.29, а, в узле В подвешен груз весом 36 кН. Соединения элементов кронштейна шарнирные. Определить усилия, возникающие в стержнях АВ и ВС, считая их невесомыми.

Решение. Рассмотрим равновесие узла В, в котором сходятся стержни АВ и ВС. Узел В представляет собой точку на чертеже. Так как груз подвешен к узлу В, то в точке В прикладываем силу F, равную весу подвешенного груза. Стержни ВА и ВС, шарнирно соединенные в узле В, ограничивают возможность любого его линейного перемещения в вертикальной плоскости, т.е. являются связями по отношению к узлу В.

Рис. 29. Расчетная схема кронштейна к примеру 7:

а – расчетная схема; б – система сил в узле B

Мысленно отбрасываем связи и заменяем их действия силами - реакциями связей R_А и R_С. Так как стержни невесомые, то реакции этих стержней (усилия в стержнях) направлены вдоль оси стержней. Предположим, что оба стержня растянуты, т.е. их реакции направлены от шарнира внутрь стержней. Тогда, если после расчета реакция получится со знаком минус, то это будет означать, что на самом деле реакция направлена в сторону, противоположную указанной на чертеже, т.е. стержень будет сжат.

На рис. 29, б показано, что в точке В приложены активная сила F и реакции связей R_А и R_С. Видно, что изображенная система сил представляет плоскую систему сил, сходящихся в одной точке. Выбираем произвольно оси координат OX и OY и составляем уравнения равновесия вида:

ΣF_x = 0; -R_a - R_ccos𝛼 = 0;

ΣF_y = 0; -F - R_c cos (90 - α) = 0.

Учитывая, что cos (90 - α) = sinα, из второго уравнения находим

R_c = -F/sinα = -36/0,5 = -72 кН.

Подставив значение R_c в первое уравнение, получим

R_a = -R_c cosα = - (-72) ∙0,866 = 62,35 кН.

Таким образом, стержень АВ - растянут, а стержень ВС - сжат.

Для проверки правильности найденных усилий в стержнях спроектируем все силы на любую ось, не совпадающую с осями X и Y, например, ось U:

ΣF_u = 0; -R_c - R_a cosα - F cos (90- α) = 0.

После подстановки значений найденных усилий в стержнях (размерность в килоньютонах) получим

- (-72) – 62,35∙0,866 - 36∙0,5 = 0; 0 = 0.

Условие равновесия выполняется, таким образом, найденные усилия в стержнях верны.

Пример 8. Балка строительных подмостей, весом которой можно пренебречь удерживается в горизонтальном положении гибкой тягой СD и шарнирно опирается на стену в точке А. Найти усилие в тяге СD, если на край подмостей встанет рабочий весом 80 кг ≈0,8 кН (рис.30, а).

Рис. 30. Расчетная схема подмостей к примеру 8:

а – расчетная схема; б – система сил действующих на подмости

Решение. Выделяем объект равновесия. В данном примере объектом равновесия является балка подмостей. В точке В на балку действует активная сила F, равная весу человека. Связями в данном случае являются неподвижный опорный шарнир А и тяга CD. Мысленно отбросим связи, заменив их действие на балку, реакциями связей (рис. 30, б). Реакцию неподвижной шарнирной опоры по условию задачи определять не нужно. Реакция в тяге CD направлена вдоль тяги. Предположим, что стержень CD растянут, т.е. реакция R_D направлена от шарнира С внутрь стержня. Разложим реакцию R_D, по правилу параллелограмма, на горизонтальную и вертикальную составляющие:

R_Dx^гор =R_D cosα;

R_Dy^верт = R_D cos(90-α) =R_D sinα.

В результате получили произвольную плоскую систему сил, необходимым условием равновесия которой является равенство нулю трех независимых условий равновесия,.

В нашем случае удобно первым записать условие равновесия в виде суммы моментов относительно моментной точки А, так как момент опорной реакции R_A относительно этой точки равен нулю:

Σm_A = 0; F∙3a - R_dy∙a = 0

или

F∙3a - R_D sinα= 0.

Значение тригонометрических функций определим из треугольника АСD:

cosα = АC/CD = 0,89,

sinα = AD/CD = 0,446.

Решая уравнение равновесия, получим R_D = 5,38 кH. (Тяж СD - растянут).

Для проверки правильности вычисления усилия в тяже CD необходимо вычислить хотя бы одну из составляющих опорной реакции R_A. Воспользуемся уравнением равновесия в виде

ΣF_y = 0; V_A + R_Dy - F = 0

или

V_A = F - R_dy.

Отсюда V_A = -1,6 кН.

Знак минус означает, что вертикальная составляющая реакции R_A на опоре направлена вниз.

Проверим правильность вычисления усилия в тяже. Используем еще одно условие равновесия в виде уравнений моментов относительно точки В.

Σm_B = 0; V_A ∙3а + R_Dy∙2a = 0;

-1,6∙3а + 5,38∙0,446∙2а = 0; 0 = 0.

Условия равновесия соблюдаются, таким образом, усилие в тяже найдено верно.

Пример 9. Вертикальный бетонный столб забетонирован нижним концом в горизонтальное основание. Сверху на столб передается нагрузка от стены здания весом 143 кН. Столб изготовлен из бетона плотностью γ= 25 кН/м³. Размеры столба показаны на рис. 31, а. Определить реакции в жесткой заделке.

Рис. 31. Расчетная схема столба к примеру 9:

а – схема загрузки и размеры столба; б – расчетная схема

Решение. В данном примере объектом равновесия является столб. Столб загружен следующими типами активных нагрузок: в точке А сосредоточенной силой F, равной весу стены здания, и собственным весом столба в виде равномерно распределенной по длине бруса нагрузки интенсивностью q на каждый метр длины столба: q = 𝛾А, где А - площадь поперечного сечения столба.

q = 25∙0,51∙0.51 = 6,5 кН/м.

Связями в данном примере является жесткая заделка в основании столба. Мысленно отбросим заделку и заменим ее действие реакциями связей (рис. 31, б).

В нашем примере рассматривается частный случай действия системы сил, перпендикулярных заделке и проходящих по одной оси через точку приложения опорных реакций. Тогда две опорные реакции: горизонтальная составляющая и реактивный момент будут равны нулю. Для определения вертикальной составляющей опорной реакции спроектируем все силы на ось элемента. Совместим эту ось с осью Z, тогда условие равновесия запишется в следующем виде:

ΣF_Z = 0; V_B - F - ql = 0,

где ql - равнодействующая распределенной нагрузки.

Отсюда

V_B = F +ql=143 + 6,5∙4 = 169 кН.

Знак плюс указывает, что реакция V_B направлена вверх.

Для проверки правильности вычисления опорной реакции остается еще одно условие равновесия - в виде алгебраической суммы моментов всех сил относительно любой точки, не проходящей через ось элемента. Предлагаем выполнить эту проверку самостоятельно.

Пример 10. Для балки, изображенной на рис.32, а, требуется определить опорные реакции. Дано: F = 60 кН, q = 24 кН/м, М = 28 кН∙м.

Рис. 32. Расчетная схема и размеры балки к примеру 10:

а – расчетная схема; б – объект равновесия

Решение. Рассмотрим равновесие балки. Балка загружена активной нагрузкой в виде плоской системы параллельных вертикальных сил, состоящих из сосредоточенной силы F, равномерно распределенной нагрузки интенсивностью q с равнодействующей Q, приложенной в центре тяжести грузовой площади (рис. 32, б), и сосредоточенного момента М, который можно представить в виде пары сил.

Связями в данной балке являются шарнирно-неподвижная опора А и шарнирно-подвижная опора В. Выделим объект равновесия, для этого отбросим опорные связи и заменим их действия реакциями в этих связях (рис. 32, б). Реакция подвижной опоры R_B направлена вертикально, а реакция шарнирно-неподвижной опоры R_A будет параллельна активной системе действующих сил и направлена также вертикально. Предположим, что они направлены вверх. Равнодействующая распределенной нагрузки Q = 4,8∙q приложена в центре симметрии грузовой площади.

При определении опорных реакций в балках необходимо стремиться так составлять уравнения равновесия, чтобы в каждое из них входило только одно неизвестное. Этого можно добиться, составляя два уравнения моментов относительно опорных точек. Проверку опорных реакций обычно проводят, составляя уравнение в виде суммы проекций всех сил на ось, перпендикулярную оси элемента.

Примем условно направление вращения момента опорных реакций вокруг моментных точек за положительное, тогда противоположное направление вращения сил будем считать отрицательным.

Необходимым и достаточным условием равновесия в данном случае является равенство нулю независимых условий равновесия в виде:

Σm_A = 0; V_B ∙6 - q∙4,8∙4,8 + M + F∙2,4 = 0;

Σm_B = 0; V_A∙6 - q∙4,8∙1,2 - M - F∙8,4 = 0.

Подставляя численные значения величин, находим

V_B = 14,4 кН, V_A = 15,6 кН.

Для проверки правильности найденных реакций используем условие равновесия в виде:

ΣF_y = 0; V_A + V_B - F -q∙4,8 =0.

После подстановки численных значений в это уравнение получаем тождество типа 0=0. Отсюда делаем выводы, что расчет выполнен верно и реакции на обеих опорах направлены вверх.

Пример 11. Определить опорные реакции для балки, изображенной на рис.33, а. Дано: F = 2,4 кН, M = 12 кН∙м, q = 0,6 кН/м, a = 60°.

Рис. 33. Расчетная схема и размеры балки к примеру 11:

а – расчетная схема; б – объект равновесия

Решение. Рассмотрим равновесие балки. Мысленно освобождаем балку от связей на опорах и выделяем объект равновесия (рис. 33, б). Балка загружена активной нагрузкой в виде произвольной плоской системы сил. Равнодействующая распределенной нагрузки Q = q∙3 приложена в центре симметрии грузовой площади. Силу F разложим по правилу параллелограмма на составляющие – горизонтальную и вертикальную

F_z = Fcosα= 2,4 cos60° = 1,2 кН;

F_y =Fcos(90-α) = F sin60° = 2,08 кН.

Прикладываем к объекту равновесия вместо отброшенных связей реакции. Предположим, вертикальная реакция V_A шарнирно подвижной опоры А направлена вверх, вертикальная реакция V_B шарнирно неподвижной опоры B направлена также вверх, а горизонтальная реакция H_В - вправо.

Таким образом, на рис. 33, б изображена произвольная плоская система сил, необходимым условием равновесия которой является равенство нулю трех независимых условий равновесия для плоской системы сил. Напомним, что, согласно теореме Вариньона, момент силы F относительно любой точки равен сумме моментов составляющих F_z и F_y относительно этой же точки. Примем условно, направление вращения момента опорных реакций вокруг моментных точек за положительное, тогда противоположное направление вращение сил будем считать отрицательным.

Тогда условия равновесия удобно составить в следующем виде:

ΣFz = 0; - F_z + H_B = 0; отсюда H_B = 1,2 кН;

Σm_A = 0; V_B∙6 + M - F_y ∙2 + 3q∙0.5 = 0; отсюда V_B = - 1,456 кН;

Σm_B = 0; V_A ∙6 - 3q∙6,5 - F_y ∙4 - M = 0; отсюда V_A = 5,336 кН.

Для проверки правильности вычисленных реакций используем еще одно условие равновесия, которое не использовали, например:

ΣF_y = 0; V_A + V_B - 3q - F_y = 0.

После подстановки численных значений получаем тождество 0=0.

Вертикальная опорной реакции V_B получилась со знаком минус, это показывает, что в данной балке она направлена не вверх, а вниз.

Пример 12. Определить опорные реакции для балки, жестко заделанной с одной стороны и изображенной на рис. 34, а. Дано: q =20 кН/м.

Рис. 34. Расчетная схема и размеры балки к примеру 12:

а – расчетная схема; б – объект равновесия

Решение. Выделим объект равновесия. Балка загружена активной нагрузкой в виде плоской системы параллельных сил, расположенных вертикально. Мысленно освобождаем балку от связей в заделке и заменяем их реакциями в виде сосредоточенной силы V_B и пары сил с искомым реактивным моментом М_B (см. рис.34, б). Так как активные силы действуют только в вертикальном направлении, то горизонтальная реакция Н_B равна нулю. Примем условно направление вращения момента опорных реакций вокруг моментных точек по часовой стрелке за положительное, тогда противоположное направление вращения сил будем считать отрицательным.

Составляем условия равновесия в виде

ΣF_y = 0; V_B - q∙1,6 = 0;

Σm_B = 0; M_B - q∙1,6∙1,2 = 0.

Здесь q∙1,6 – равнодействующая распределенной нагрузки.

Подставив численные значения распределенной нагрузки q, находим

V_В = 32 кН, М_B = 38,4 кН∙м.

Для проверки правильности найденных реакций составим еще одно условие равновесия. Теперь возьмем за моментную точку какую-нибудь другую точку, например правый конец балки, тогда:

Σm_A = 0; M_B – V_B∙2 + q∙1,6∙0,8 = 0 .

После подстановки численных значений получаем тождество 0=0.

Окончательно делаем выводы, что опорные реакции найдены верно. Вертикальная реакция V_B направлена вверх, а реактивный момент М_В - по часовой стрелке.

Пример 13. Определить опорные реакции балки (рис.35, а).

Решение. В качестве активной нагрузки выступает равнодействующая распределенной нагрузки Q=(1/2)∙aq=(1/2)∙3∙2=3кН, линия действия которой проходит на расстоянии 1 м от левой опоры, сила натяжения нити Т = Р = 2 кН, приложенная на правом конце балки и сосредоточенный момент.

Поскольку последний можно заменить парой вертикальных сил, то действующая на балку нагрузка вместе с реакцией подвижной опоры В образует систему параллельных сил, поэтому реакция R_A будет также направлена вертикально (рис.35, б).

Для определения этих реакций воспользуемся уравнениями равновесия.

ΣM_A = 0; -Q∙1 + R_В∙3 - M + Т∙5 = 0,

откуда

R_В = (1/3) (Q + M - Р∙5) = (1/3) (3 + 4 - 2∙5) = -1 кН.

ΣM_B = 0; - R_A∙3 + Q∙2 - M + Т∙2 = 0,

R_A = (1/3) (Q∙2 - M + Р∙2) = (1/3) (3∙2 - 4 + 2∙2) = 2 кН.

Рис.35

Чтобы проверить правильность полученного решения, воспользуемся дополнительным уравнением равновесия:

ΣY_i = R_A - Q + R_В + Т = 2 - 3 - 1 + 2 = 0,

то есть, задача решена правильно.

Пример 14. Найти опорные реакции консольной балки, загруженной распределенной нагрузкой (рис.36, а).

Решение. Равнодействующая распределенной нагрузки приложена в центре тяжести грузовой эпюры. Чтобы не искать положение центра тяжести трапеции, представим ее в виде суммы двух треугольников. Тогда заданная нагрузка будет эквивалентна двум силам: Q₁ = (1/2)∙3∙2 = 3 кН и Q₂ = (1/2)∙3∙4 = 6 кН, которые приложены в центре тяжести каждого из треугольников (рис.36,б).

Рис.36

Опорные реакции жесткого защемления представлены силой R_A и моментом M_A, для определения которых удобнее использовать уравнения равновесия системы параллельных сил, то есть:

ΣM_A = 0; M_A = 15 кН∙м;

ΣY = 0, R_A = 9 кН.

Для проверки воспользуемся дополнительным уравнением ΣM_В = 0, где точка В находится на правом конце балки:

ΣM_В = M_A - R_A∙3 + Q₁∙2 + Q₂∙1 = 15 - 27 + 6 +6 = 0.

Пример 15. Однородная балка весом Q = 600 Н и длиной l = 4 м опирается одним концом на гладкий пол, а промежуточной точкой В на столб высотой h = 3 м, образуя с вертикалью угол 30°. В таком положении балка удерживается веревкой, протянутой по полу. Определить натяжение веревки T и реакции столба - R_B и пола - R_A (рис.37,а).

Решение. Под балкой или стержнем в теоретической механике понимают тело, у которого поперечными размерами в сравнении с его длиной можно пренебречь. Таким образом, вес Q однородной балки приложен в точке С, где АС = 2 м.

Рис.37

1) Поскольку две неизвестных реакции из трех приложены в точке А, первым следует составить уравнение ΣM_A = 0, так как туда войдет только реакция R_B:

- R_B ∙АВ+ Q∙(l/2)∙sin30° = 0,

где АВ = h/cos30°= 2 м.

Подставляя в уравнение, получим:

R_B ∙2 = 600∙2∙(1/2) = 600,

откуда

R_B = 600/ (2) = 100 ≅ 173 Н.

Аналогично из моментного уравнения можно было бы найти и реакцию R_A, выбрав в качестве моментной точку, где пересекаются линии действия R_B и Т. Однако это потребует дополнительных построений, поэтому проще воспользоваться другими уравнениями равновесия:

2) ΣX = 0; R_B ∙cos30° - Т = 0; → Т = R_B ∙cos30°= 100 ∙(/2) = 150 Н;

3) ΣY = 0, R_B∙sin30°- Q + R_A = 0; → R_A = Q - R_B∙sin30°= 600 - 50 ≅ 513 Н.

Таким образом, мы нашли Т и R_A через R_B , поэтому проверить правильность полученного решения можно с помощью уравнения: ΣM_B = 0, куда в явном или неявном виде войдут все найденные реакции:

R_A∙АВ sin30°- Т∙АВ cos30° - Q∙(АВ - l/2)∙sin30°= 513∙2 ∙(1/2) - 150∙2 ∙( /2) - 600∙ (2 - 2)∙(1/2) = 513∙ - 150∙3 - 600∙( -1) ≅ 513∙1,73 - 450 - 600∙0,73 = 887,5 - 888 = -0,5.

Полученная в результате округления невязка ∆= -0,5 называется абсолютной погрешностью вычисления.

Для того чтобы ответить на вопрос насколько точным является полученный результат, вычисляют относительную погрешность, которая определяется по формуле:

ε=[|∆| / min(|Σ⁺|, |Σ^-|)]∙100% =[|-0,5| / min(|887,5|, |-888|)]∙100% = (0,5/887,5)∙100% = 0,06%.

Пример 16. Определить опорные реакции рамы (рис.38). Здесь и в дальнейшем, если не оговорено специально, все размеры на рисунках будем считать указанными в метрах, а силы - в килоньютонах.

Рис.38

Решение. Рассмотрим равновесие рамы, к которой в качестве активной приложена сила натяжения нити Т, равная весу груза Q.

1) Реакцию подвижной опоры R_B найдем из уравнения ΣM_A = 0. Чтобы при этом не вычислять плечо силы Т, воспользуемся теоремой Вариньона, разложив эту силу на горизонтальную и вертикальную составляющие:

R_B∙2 + Т sin30°∙3 - Т cos30°∙4 = 0; → R_B = (1/2)∙ Q(cos30°∙4 - sin30°∙3) = (5/4) ∙ (4- 3) кН.

2) Для вычисления Y_A составим уравнение ΣM_С = 0, где точка С лежит на пересечении линий действия реакций R_B и Х_A:

- Y_A∙2 + Т sin30°∙3 - Т cos30°∙2 = 0; → Y_A = (1/2)∙ Q(sin30°∙3 -cos30°∙2) = (5/4) ∙ (3 -2) кН.

3) Наконец, находим реакцию Х_A:

ΣX = 0; Х_A - Т sin30° = 0; → Х_A = Q sin30° = 5/2 кН.

Поскольку все три реакции были найдены независимо друг от друга, для проверки нужно взять уравнение, в которое входит каждая из них:

ΣM_D = Х_A∙3 - Y_A∙4 - R_B∙2 = 15/2 - 5∙(3 -2) - (5/2)∙ (4- 3) = 15/2 - 15 + 10 -10 +15/2 = 0.

Пример 17. Определить опорные реакции стержня, имеющего ломаное очертание (рис.39,а).

Решение. Заменяем распределенную нагрузку на каждом участке стержня сосредоточенными силами Q₁ = 5 кН и Q₂ = 3 кН, а действие отброшенного жесткого защемления - реакциями Х_A ,Y_A и M_А (рис.39,б).

Рис.39

1) ΣM_А = 0; M_А -Q₁∙2,5 - Q₂∙5,5 = 0; → M_А = 5∙2,5 + 3∙5,5 = 12,5 + 16,5 = 29 кНм.

2) ΣX = 0; Х_A + Q₁∙sina = 0; → Х_A = -5∙(3/5) = -3 кН.

3) ΣY = 0; Y_A - Q₁ cosa - Q₂ = 0; → Y_A = 5∙(4/5) + 3 = 4 + 3 = 7 кН, так как sinα = 3/5, cosα = 4/5.

Проверка: ΣM_В = 0; M_А + Х_A∙3 - Y_A∙7 + Q₁cosα∙4,5 + Q₁sinα∙1,5 + Q₂∙1,5 = 29 -3∙3 - 7∙7 + 5∙(4/5)∙5 + 5∙(3/5)∙1,5 + 3∙1,5 = 29 - 9 - 49 + 20 + 4,5 + 4,5 = 58 - 58 = 0.

Пример 18. Для рамы изображенной на рис.40, а, требуется определить опорные реакции. Дано: F = 50 кН , М = 60 кН∙м , q = 20 кН/м.

Решение. Рассмотрим равновесие рамы. Мысленно освобождаем раму от связей на опорах (рис.40, б) и выделяем объект равновесия. Рама загружена активной нагрузкой в виде произвольной плоской системы сил. Вместо отброшенных связей прикладываем к объекту равновесия реакции: на шарнирно-неподвижной опоре А - вертикальную V_A и горизонтальную H_A, а на шарнирно-подвижной опоре В - вертикальную реакцию V_B Предполагаемое направление реакций показано на рис.40, б.

Рис.40. Расчетная схема рамы и объект равновесия к примеру 18:

а – расчетная схема; б – объект равновесия

Составляем следующие условия равновесия:

ΣF_x = 0; -H_A + F = 0; H_A = 50 кН.

Σm_A = 0; V_B∙6 + M - q∙6∙3 - F∙6 = 0; V_B = 100 кН.

ΣF_y = 0; V_A + V_B - q∙6 = 0; V_A = 20 кН.

Здесь условно принято направление вращения вокруг моментных точек против движения часовой стрелки за положительное.

Для проверки правильности вычисления реакций используем условие равновесия, в которое входили бы все опорные реакции, например:

Σm_C = 0; V_B∙3 + M – H_A∙6 – V_A∙3 = 0.

После подстановки численных значений получаем тождество 0=0.

Таким образом, направления и величины опорных реакций определены верно.

Пример 19. Определить опорные реакции рамы (рис.41,а).

Рис.41

Решение. Как и в предыдущем примере, рама состоит из двух частей, соединенных ключевым шарниром С. Распределенную нагрузку, приложенную к левой части рамы, заменяем равнодействующей Q₁, а к правой - равнодействующей Q₂, где Q₁ = Q₂ = 2кН.

1) Находим реакцию R_B из уравнения ΣM_С^(ВС) = 0; → R_B = 1кН;

Рассмотрим равновесие всей рамы как абсолютно твердого тела. Поскольку Q₁, Q₂ и R_B образуют систему параллельных сил, реакции в точке А будут представлены вертикально направленной силой R_А и реактивным моментом М_А (рис.37,б), поэтому можно составить следующие уравнения равновесия:

2) ΣM_А = 0; → M_А = 4 кН∙м;

3) ΣY = 0; → R_А = 3 кН.

Проверка:

ΣM_С^(АС) = M_А - R_А∙2 + Q₁∙1 = 4 - 3∙2 + 2∙1 = 6 - 6 = 0.

Пример 20. Определить опорные реакции рамы (рис.42,а).

Рис.42

Решение. В отличие от двух предыдущих примеров формальное определение опорных реакции в этой задаче требует совместного рассмотрения системы уравнений:

ΣM_А =0; M + Y_В∙3 - X_B∙1 = 0;

ΣM_С^(СВ) =0; M + Y_В∙1 + X_B∙1 = 0.

Ее решением будет: X_B = -M/2; Y_В = -M/2.

Рассматривая затем равновесие всей рамы в целом, получим:

ΣХ = 0; X_А + X_B = 0; → X_А = M/2;

ΣY = 0; Y_А + Y_В = 0; → Y_А = M/2.

Проверка. ΣM_С^(АС) = X_А∙1 - Y_А∙3 + M =M/2 - M/2 + M = 0.

Пример 21. Определить реакции в опорах и в соединительном шарнире трехшарнирной арки (рис.43,а).

Рис.43

Решение. Находим опорные реакции:

1) ΣM_А = 0; → Y_В = Р/2;

2) ΣM_С^(СВ) = 0; → Х_В = -Р/2;

3) ΣM_В= 0; → Y_А = Р/2;

4) ΣХ = 0; → X_А = Р/2.

Для определения реакций в соединительном шарнире нужно рассмотреть равновесие одной из частей рамы. При этом результат будет зависеть от того, к какой части считать приложенной силу Р. Например, считая эту силу приложенной к телу АС, получим из условий равновесия левой части (рис.43,б):

ΣХ^(АС) = 0; → X_C = –Р/2;

ΣY^(АС) = 0; → Y_C = -Р/2.

А если считать силу Р поделенной поровну между левой и правой частями рамы, то Y_C будет равняться нулю. В общем случае эту силу можно поделить в любом соотношении между частями рамы, но в сумме с реакцией Y_C она всегда будет равняться - Р/2.

Пример 22. Определить графически опорные реакции рамы, изображенной на рис.44.

Рис.44

Решение. Система состоит из двух тел, имеющих равное число алгебраических неизвестных: 4 - для АС (X_A, Y_A, X_C, Y_C) и 4 - для ВС (X_B, Y_B, X_C’, Y_C’), но на тело АС действуют три силы (P, R_A, R_C), а на ВС - только две (R_В, R_C’), поэтому начинаем решение с рассмотрения тела ВС.

Согласно второй аксиоме R_В и R_C’ действуют вдоль прямой, соединяющей точки их приложения, то есть по прямой ВС.

Рассмотрим равновесие всей рамы АВС как твердого тела. На нее действует уравновешенная система трех непараллельных сил, которая в силу теоремы о трех силах должна быть сходящейся, поэтому реакция R_A должна проходить через точку К, где пересекаются линии действия R_В и R_C’ (рис.44,а).

Строим силовой треугольник, проводя через начало и конец вектора Р прямые, параллельные направлениям R_A и R_В до их пересечения (рис.44,б).

Из подобия силового треугольника Oab и треугольника ВАК на чертеже находим искомые реакции:

R_В /P = ()/4; → R_В = ()/4; X_В = - (R_В)/2 = -P/4; Y_В = P/4.

|X_А| /P = 3/4; X_А = -(3/4)P; Y_А = -P/4.

Пример 23. Определить графически опорные реакции рамы, показанной на рис.45.

Рис.45

Решение. Начинаем рассмотрение с части, на которую действуют только две силы, и по аксиоме 2 определяем линию действия R_A (рис.45).

Рассматривая равновесие рамы в целом, приходим к заключению, что опорные реакции R_A и R_В должны составить пару, которая уравновесит приложенный к раме момент. Отсюда следует, что R_A = R_В = М/, при этом

X_А = Y_А = R_A (/2) = М/2; X_В = Y_В = -М/2.

Примечания к решению задач:

1. При решении задач с большим числом нагрузок – например, при выполнении расчетно-проектировочных работ все вычисления удобнее делать в десятичных дробях. В этом случае все результаты и проверка будут получаться с некоторым приближением, но относительная погрешность независимо от величин определяемых реакций и даже при использовании самых скромных вычислительных средств не должна выходить за пределы 1%.

2. Если проверка не выполняется и не удается найти ошибку, то нужно, во-первых, постараться ее локализовать, то есть выяснить, какие из вычисленных реакций найдены неверно, и воспользоваться для их определения альтернативными уравнениями. Во-вторых, можно воспользоваться следующим приемом, который вытекает из свойств систем линейных алгебраических уравнений: опорные реакции от заданной нагрузки равны сумме опорных реакций от каждой нагрузки в отдельности.

Вопросы для самопроверки

- Какая система сил называется сходящейся?

- Как определить равнодействующую системы сходящихся сил путем построения силового многоугольника?

- Какие силы называются сходящимися? Как определить их равнодействующую?

- Что называется главным вектором плоской системы сил?

- Что называется главным моментом плоской системы сил относительно какого-нибудь центра?

- Составьте условие равновесия для произвольной плоской системы сил.

- Запишите уравнения равновесия для плоской системы: а) параллельных сил; б) сходящихся сил.

- Составьте условие равновесия для системы сходящихся сил.

- Сформулируйте геометрический и аналитический методы определения равнодейстующей плоской и пространственной системы сходящихся сил?

- Составьте условие равновесия для плоской системы параллельных сил.

- Сформулируйте геометрическое условие равновесия системы сходящихся сил.

- Что называется главным вектором системы сил?

- В чем различие между главным вектором и равнодействующей системы сил?

- Для какой системы сил равнодействующая и главный вектор совпадают?

- Назовите методы определения равнодействующей системы сходящихся сил.

- Как выражаются проекции равнодействующей системы сходящихся сил через проекции сил этой системы?

- Определите величину силы по известным проекциям =3кН; 4кН.

- Определить модуль и направления силы, если известны ее проекции =30H; =40H.

- Назовите необходимое и достаточное условие равновесия системы сходящихся сил.

- Что такое силовой многоугольник?

- Имеет ли значение порядок расположения сил при построении силового многоугольника?

- В каком случае силовой многоугольник замкнутый?

- Запишите условие равновесия системы сходящихся сил в векторной форме.

- Сформулируйте условия равновесия системы сходящихся сил в координатной форме.

- Какие задачи позволяют решать условия равновесия системы сходящихся сил?

- Какой из силовых многоугольников на рисунке относится к уравновешенной системе сходящихся сил?

- Как определяется направление равнодействующей системы сходящихся сил при построении силового многоугольника?

- Каковы условия и каковы уравнения равновесия системы сходящихся сил, расположенных в пространстве и плоскости?

- Возможно ли равновесие трех сходящихся сил, не лежащих в одной плоскости?

- Обязательно ли будет находиться в равновесии тело, если на него в одной плоскости действуют три силы и линии их действия пересекаются в одной точке?

- Что называется равнодействующей системы сил?

- Как сложить силы:

а) геометрически,

б) аналитически?

- Как разложить силу по двум заданным направлениям?

- Что называется моментом силы относительно центра на плоскости?

- Как проектируется сила на ось и на плоскость? Чем отличаются эти проекции и как они вычисляются?

- Дайте определение векторного момента силы относительно точки. Каковы способы его вычисления?

- Сформулируйте теорему о равновесии трех непараллельных сил?

- Изменится ли момент силы относительно точки при переносе силы вдоль линии действия?

- В каком случае момент силы относительно точки равен нулю?

- Какая система сил называется парой?

- Чем характеризуется пара сил? Каковы свойства пар?

- Можно ли заменить действие пары сил на тело одной силой?

- Что такое момент пары?

- Какая плоскость называется плоскостью действия пары?

- Какие пары называются эквивалентными?

- Что называется плечом пары?

- Запишите векторную и скалярную зависимости между элементами пары.

- Почему пара сил не имеет равнодействующей?

- Имеет ли пара сил равнодействующую?

- Каким образом можно уравновесить действие на тело пары сил?

- Что такое момент пары сил?

- Как направлен и чему равен по модулю вектор-момент пары сил?

- Изменятся ли моменты пар сил, если положения сил, показанные на рис. а, изменить на положения, показанные на рис. б?

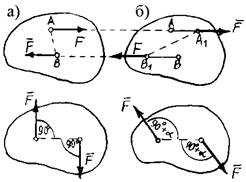
- Какие пары называются эквивалентными?

- При каком условии две пары будут эквивалентны?

- Эквивалентны ли пары сил, изображенные на рисунке?

- Каким образом производится сложение пар сил?

- Сформулируйте условие равновесия пар сил.

- Какие уравнения и сколько их можно составить для уравновешенной плоской системы сходящихся сил?

- Сформулируйте теорему о равновесии трех непараллельных сил, лежащих в одной плоскости.

- Чем характеризуется действие пары сил на твердое тело?

- Как направлен вектор момента пары сил?

- Как определяются моменты пар сил, лежащих в одной плоскости?

- Каковы условия эквивалентности пар сил на плоскости и в пространстве?

- Какие преобразования пары сил не изменяют ее действия на твердое тело?

- Почему момент пары сил является свободным вектором?

- Чему равен момент пары сил, эквивалентной двум парам сил, расположенным в пересекающихся плоскостях?

- Чему равен момент пары сил, эквивалентной системе пары сил, расположенных в пространстве и в одной плоскости?

- Каковы условия равновесия системы пар сил, расположенных в пространстве и в одной плоскости?

- Чем можно уравновесить заданную пару сил?

- Чем характеризуется система распределенных сил?

- Как определить равнодействующую системы распределенных сил?

- Перечислите виды нагрузок, действующих на твердое тело.

- Какое тело называется несвободным? Приведите примеры.

- Сформулируйте принцип освобождаемости от связей.

- Как направлены реакции наиболее распространенных связей: гладкой поверхности, подвижного и неподвижного шарниров, жесткой заделки, идеального стержня, нити?

- Как направлены реакции опор балки, нагруженной парой сил и лежащей на двух опорах, из которых одна – шарнирно-неподвижная, а другая – на катках?

- Какова последовательность действий при определении опорных реакций?

- Какой третьей парой сил можно уравновесить две пары сил, лежащие в пересекающихся плоскостях?

- Сформулируйте теоремы об эквивалентности пар.

- Что называется результирующей парой?

- Запишите формулу для определения результирующей системы пар.

- Назовите условия равновесия плоской системы пар.

- Приведите векторную запись условия равновесия произвольной системы пар.

- При каких условиях плоская система сил приводится к равнодействующей?

- Чему равен главный вектор плоской системы сил, которая может быть приведена к равнодействующей?

- В каком случае главный момент плоской системы сил не зависит от выбора центра приведения?

- Что такое момент силы относительно точки?

- Будет ли изменяться момент силы относительно точки, если, не меняя направления, переносить силу вдоль линии ее действия?

- На тело действуют две силы F₁ = 40 Н и F₂ = 50 Н, как показано на рисунке (а = 0,5 м, b = 0,8 м, ). Какая из сил создает больший момент относительно точки О?

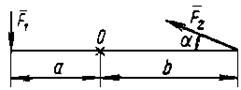
- Что такое главный вектор и главный момент плоской системы сил?

- Как аналитически найти главный вектор и главный момент данной плоской системы сил?

- В чем сходство и в чем различие между главным вектором плоской системы сил и ее равнодействующей?

- Сформулируйте теорему Вариньона.

- Приведите векторную запись теоремы Вариньона.

- Сформулируйте теорему Вариньона для произвольной плоской системы сил.

- Чему равен главный вектор системы сил?

- Чему равен главный момент системы сил при приведении ее к точке?

- Тело движется равномерно и прямолинейно (равновесие). Чему равны главный вектор и главный момент системы?

- Тело вращается вокруг неподвижной оси. Чему равны главный вектор и главный момент действующей на него системы сил?

- Зависят ли главный вектор и главный момент заданной системы сил от выбора центра приведения?

- Каковы возможные случаи приведения сил, расположенных произвольно на плоскости?

- К какому простейшему виду можно привести систему сил, если известно, что главный момент этих сил относительно различных точек на плоскости:

а) имеет различную числовую величину;

б) имеет постоянное значение, не равное нулю;

в) равен нулю.

- Как определяется модуль и направление главного вектора системы параллельных сил на плоскости?

- При каком условии сила, равная главному вектору плоской системы сил, является равнодействующей этой системы?

- Каковы условия и уравнения равновесия плоской системы параллельных сил на плоскости?

- Какое твердое тело называют рычагом?

- Какое условие выполняется, когда рычаг находится в покое?

- Чему равен главный вектор и главный момент произвольной плоской системы сил?

- Сформулируйте три формы уравнений равновесия произвольной плоской системы сил.

- Какие задачи статики называют статически определимыми и какие статически неопределимыми?

- Какую из форм уравнения равновесия целесообразно использовать при определении реакций в заделке?

- Какую из форм уравнения равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?

- В чем сущность решения задач на равновесие сочлененной системы тел?

- Какие системы называют составными?

- Приведите примеры составных коснтрукций, в которых тела соединяются шарнирами, и покажите силы взаимодействия между частями этих конструкций.

- Как направлены силы взаимодействия, если тела, входящие в систему, касаются друг друга гладкими поверхностями?

- Какими реакциями заменяют связи различных типов?

- Какие силы в составных конструкциях называют внешними?

- В чем состоит задача статики при рассмотрении системы твердых тел?

- Сколько уравнений равновесия можно составить для системы из N тел на плоскости?

- Какие варианты составления уравнений равновесия для составной конструкции можно рассмотреть?

- Как рационально выбрать оси координат и моментные точки при составлении уравнений равновесия?

- Какой вид будут иметь уравнения равновесия, если на систему действует плоская система параллельных или сходящихся сил?

- Невесомый груз нагружен силой F, как показано на рисунке. Определите (воспользовавшись, если нужно, только калькулятором), под каким углом к брусу направлена реакция шарнира А.

Ответ: а) ; б) .

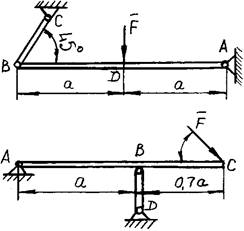
- Чтобы определить момент силы необходимо знать:

1) силу и плечо силы;

2) плечо силы;

3) направление силы;

4) пару сил;

5) расстояние и силу.

- Какой вектор в механике называют скользящим?

1) вектор равнодействующей системы сил;

2) вектор силы;

3) вектор скорости.

- Какую способность силы характеризует момент?

1) вращательную способность силы;

2) способность силы совершать поступательное движение;

3) способность силы быть перемещенной по линии ее действия.

- Что такое пара сил?

1) система двух сил, линии действия которых параллельны;

2) система двух сил, равных по модулю и противоположных по направлению;

3) система двух равных по модулю, параллельных, направленных в противоположные стороны и не лежащих на одной прямой сил действующих на абсолютно твердое тело.

- Что называется интенсивностью распределения нагрузки?

1) это значение силы, приходящейся на единицу длины нагруженного отрезка;

2) это сила, которая заменяет действие на тело распределенной силы;

3) это сила, численно равная площади распределенной нагрузки.

- В многоугольнике сил, какой вектор изображает равнодействующую силу

1)

2)

3)

4)

5)

- В многоугольнике сил, какой вектор изображает равнодействующую силу

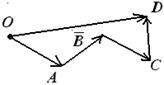
1)

2)

3)

4)

5)

- При каком значении угла между силой и осью проекция силы равна нулю?

1) =0;

2) =90°;

3) =180°.

- Если проекция силы на ось = 8 кН , = 3 кН, то действующая сила равна:

1)

2)

3)

4)

5)

- Если проекция силы на ось = 8 кН , = 6 кН, то действующая сила равна:

1) =10 кН;

2) кН;

3) кН;

4) =11 кН;

5) =12 кН.

- При каком значении угла , проекция силы P на ось y равна нулю

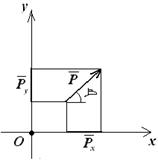
1)

2) ;

3)

4)

5)

- При каком значении угла , проекция силы P на ось y равна нулю?

1)

2) ;

3)

4)

5)

- Определить проекцию равнодействующей силы на ось y, если известны проекции каждого из слагаемых векторов:

1) =40 H;

2) =60 H;

3) = -100 H;

4) = -120 H.

- Определить модуль равнодействующей системы сходящихся сил, если проекции слагаемых векторов равны:

1) =50 H;

2) = -30 H;

3) =60 H;

4) =70 H;

5) = -70 H;

6) =40 H;

7) =80 H;

8) = -90 H.

- В каком из указанных случаев плоская система сходящихся сил уравновешена?

1)

2)

3)

4)

- Что определяет эффект действия пары сил?

1) произведение силы на плечо;

2) момент пары и направление поворота.

- Чем можно уравновесить пару сил?

1) одной силой;

2) парой сил.

- Зависит ли эффект действия пары сил на тела от его положения в плоскости?

1) да;

2) нет.

- Какие из приведенных ниже пар эквивалентны?

1) а) сила пары 100 кН, плечо 0,5 м; б) сила пары 20 кН, плечо 2,5 м; в) сила пары 1000 кН, плечо 0,05 м. Направление всех трех пар одинаково.

2) а) М₁=-300 Нм; б) М₂=300 Нм.

- Момент пары сил равен 100 Нм, плечо пары 0,2 м. Определить значении сил пары? Как изменится значение сил пары, если плечо увеличить в два раза при сохранении численного значения момента?

- Будет ли тело находиться в равновесии, если на него действуют три пары сил, приложенных в одной плоскости, и моменты этих пар имеют следующие значения: М₁=-600 Нм; М₂=320 Нм и М₃=280 Нм.

1) тело будет находиться в равновесии;

2) тело не будет находиться в равновесии.

- Зависит ли значение и направление момента силы относительно точки от взаимного расположения этой точки и линии действия силы?

1) не зависит;

2) зависит.

- Когда момент силы относительно оси равен нулю?

1) когда силы параллельно оси;

2) когда линия действия силы пересекает ось;

3) Когда сила и ось расположены в одной плоскости.

- Зависит ли момент присоединенной пары сил от расстояния точки приведения до линии действия силы?

1) зависит;

2) не зависит.

- Зависит ли значение и направление главного вектора от положения центра приведения?

1) не зависит;

2) зависит.

- Зависит ли значение и знак главного вектора от положения центра приведения?

1) не зависит;

2) зависит.

- Можно ли определить алгебраическую сумму моментов сил относительно некоторой точки О, если задана только равнодействующая этих сил и ее плечо а относительно этой точки?

1) нельзя;

2) можно.

- Чем отличается главный вектор от равнодействующей плоской системы произвольно расположенных сил?

1) величиной;

2) направлением;

3) величиной и направлением;

4) точкой приложения;

5) ничем.

- Главный вектор системы сил определяется по формуле:

1)

2)

3)

4)

5)

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00