Главная
Тестовые
вопросы по теме "Динамика системы и твердого тела"
- Число степеней свободы данной системы равно...
1. нулю
2. трем
3. двум
4. единице
- Число степеней свободы данной системы равно...
1. двум
2. нулю
3. единице
4. трем
- Число степеней свободы данной системы равно...
1. двум
2. нулю
3. единице
4. трем
- Число степеней свободы данной системы равно...
1. нулю
2. трем
3. двум
4. единице
- Число степеней свободы данной системы равно...
1. нулю
2. трем
3. двум
4. единице
- Момент инерции тела относительно оси это …
1. произведение силы инерции тела на расстояние до оси вращения
2. произведение масс материальных точек, составляющих тело на
расстояние от каждой точки до оси
3. отношение вращающего момента к массе вращающегося тела
4. сумма произведений масс материальных точек, составляющих тело, на квадрат
расстояний от них до оси
- Метод кинетостатики (принцип Даламбера) основан на…
1. принципе независимости действия сил
2. гипотезе Бернулли
3. уравновешивании сил, действующих на точку, силами инерции
4. выводах из закона Гука
- Принцип Даламбера формулируется следующим образом?
1. При движении системы сумма работ всех активных сил и сил инерции системы
равных нулю
2. В каждый момент времени заданные силы и реакции связей,
действующие на материальную точку (тело) как бы уравновешиваются силой инерции
3. Сумма работ всех внешних и внутренних сил, приложенных к
системе равна изменению количества движения системы
- Движением по инерции называют ... движение
1. равномерное прямолинейное
2. равномерное по дуге окружности
3. равноускоренное прямолинейное
4. равнозамедленное прямолинейное
- Для уравновешивания вращающегося тела (ротора) необходимо чтобы…
1. его эксцентриситет был максимальным
2. его центр тяжести лежал на оси вращения
3. угловая скорость вращения не превышала предельные значения для
данной массы ротора
4. радиус инерции ротора не превышал его эксцентриситет
- Если (m) – масса
точки, (c) – центр масс, (
)
– скорость центра масс, то 
- это...
1. момент сил инерции твердого
тела
2. кинетический момент твердого
тела относительно оси
3. количество движения твердого
тела
4. кинетическая энергия твердого
тела при вращательном движении
5. кинетическая энергия
материальной точки
- Если (m) – масса
точки, (V) – скорость точки, то 
- это...
1. кинетическая энергия
материальной точки
2. нормальная сила инерции точки
3. кинетический момент точки
относительно оси
4. касательная сила инерции точки
5. количество движения точки
- Если (m) – масса
точки, (V) – скорость точки, (ρ) – радиус кривизны траектории, то
- это...
1. кинетическая энергия
материальной точки
2. нормальная сила инерции точки
3. кинетический момент твердого
тела относительно оси
4. момент сил инерции твердого
тела
5. нормальная сила инерции точки
- Если (m) – масса
точки, (с) – центр масс, (v) – скорость точки, то 
- это...
1. момент сил инерции твердого
тела
2. кинетический момент твердого
тела относительно оси
3.количество движения твердого
тела
4. кинетическая энергия твердого
тела при поступательном движении
5. кинетическая энергия материальной
точки
- Если (I) – момент
инерции тела, (ω) – угловая
скорость тела, то 
- это...
1. момент сил инерции твердого
тела
2. кинетический момент твердого
тела относительно оси
3.количество движения твердого
тела
4. кинетическая энергия твердого
тела при вращательном движении
5. кинетическая энергия
материальной точки
- Центробежная сила инерции при криволинейном движении всегда
направлена…
1. от мгновенного центра кривизны траектории
2. по касательной к траектории в сторону, противоположную ускорению
3. по касательной к траектории в сторону ускорения
4. к мгновенному центру кривизны траектории
- Теорема об изменении кинетического момента системы
материальных точек относительно центра гласит первая производная по времени от
кинетического момента системы материальных точек относительно центра равна
главному моменту всех … сил относительно данного центра:
1. внешних
2. активных
3. внутренних
- Сила инерции и ускорение точки направлены ...
1. по одной прямой в противоположные стороны
2. по одной прямой в одну и ту же сторону
3. под некоторым углом друг к другу
4. перпендикулярно друг другу
- Мерой отклонения движения от движения по инерции является ...
1. масса
2. скорость
3. время
4. ускорение
- Эксцентриситет массы ротора – это…
1. произведение массы ротора на квадрат смещения центра тяжести относительно
оси вращения
2. отношение момента инерции ротора к его массе
3. расстояние от центра тяжести ротора до оси вращения
4. смещение радиуса инерции ротора относительно оси вращения
- Масса механической системы?
1. 
2. 
3. 
4. 
5. 
- Масса механической системы?
1. 
2. 
3. 
4. 
5. 
- Если (mi) – масса
точки, (
)
– скорость точки, (n) – количество точек, то 
это...
1. кинетическая энергия системы материальных точек
2. кинетический момент твердого тела относительно оси
3. главный вектор количества движения системы материальных точек
4. кинетическая энергия твердого тела при вращательном движении
5. кинетическая энергия материальной точки
- Тело 1 поднимается с ускорением a = 3 м/с2, массы тел m1 = m2 = 20кг, радиус барабана 2, который можно считать однородным цилиндром, r = 0,1м (g = 10 м/с2). Тогда модуль момента М пары сил равен...
1. 27 Нм
2. 17 Нм
3. 29 Нм
4. 11 Нм
- Тело 1 поднимается массой m1 = 3 кг поднимается с постоянным ускорением a = 2 м/с2, массой ступенчатого блока можно пренебречь, считать R=2r (g = 10 м/с2). Тогда модуль силы F будет равен...
1. 3 Нм
2. 15 Нм
3. 12 Нм
4. 18 Нм
- Тело 1 массой m1 = 3 кг поднимается с постоянным ускорением a = 2 м/с2 (g = 10 м/с2). Тогда модуль силы F будет равен...
1. 36 Н
2. 6 Н
3. 30 Н
4. 24 Н
- Центр С однородного сплошного катка 1, масса которого m1 = 5 кг, радиус r = 0,4м, движется вверх с постоянным ускорением ac = 2м/с2 (g = 10 м/с2). Тогда модуль силы F будет равен...
1. 40 Н
2. 65 Н
3. 70 Н
4. 45 Н
- Тело 1 массой m1 = 3 кг поднимается по шероховатой наклонной плоскости с постоянным ускорением a = 1 м/с2. Коэффициент трения скольжения f=0,12, масса блока m2 = 2 кг равномерно распределена по ободу блока (g = 10 м/с2). Тогда модуль силы F будет равен (округлить до целого значения)...
1. 8 Н
2. 19 Н
3. 13 Н
4. 23 Н
- Центр С катка 1, масса которого m1 = 5 кг равномерно распределена по ободу, радиус r=0,4 м, движется вверх с постоянным ускорением ac = 2 м/с2 (g = 10 м/с2). Тогда модуль силы F будет равен...
1. 25 Н
2. 40 Н
3. 45 Н
4. 30 Н
- Регулятор Уатта в установившемся движении при угловой скорости вращения ω = 12с-1 имеет момент инерции I = 40кгм2. Сопротивление вращению пренебрегаем. В случае сохранения кинетического момента при угловой скорости ω1 = 3с-1 момент инерции I1 равен...
1. 10
2. 120
3. 240
4. 160
- Сплошной однородный диск массы 6 кг и радиуса R = 2м катится без скольжения по
горизонтальной поверхности. Скорость центра масс диска изменяется по закону Vc = 2t + 11 [м/с], где 
- время в секундах. Модуль главного вектора сил инерции
равен...Н.
1. 12
2. 16
3. 13
4. 15
5. 14
- Ступенчатое колесо радиуса R, масса
которого m равномерно
распределена по окружности радиуса R, катится по
прямолинейному горизонтальному рельсу без проскальзывания, касаясь рельса
ободом r(R=3r), имея
ускорение в центре масс 
.
Тогда главный вектор сил инерции колеса по модулю равен...
1.
2. 2ma
3. ma
4. 0
- Диск радиуса R и массой m, которая равномерно распределена по тонкому стержню,
проходящему через центр, катится по горизонтальной плоскости, имея ускорение в
центре масс .
Тогда главный вектор сил инерции диска по модулю равен...
1. 2ma
2. 0
3. ma
4.
- Диск радиуса R и массой m, которая равномерно распределена по тонкому стержню,
проходящему через центр диска, вращается относительно оси, проходящей через т. О, лежащую на ободе перпендикулярно
плоскости диска, имея ускорение в центре масс .
Тогда главный вектор сил инерции колеса по модулю равен...
1. 0
2. ma
3. 
4. 
- Колесо радиуса R, масса которого m равномерно распределена по ободу,
жестко прикреплен к невесомому стержню длиной l=R, который вращается относительно оси, проходящей через его конец О
перпендикулярно плоскости диска, имея в т.С
скорость 
.
Количество движения колеса равно...
1. 
2. mV
3. 0
4. 
- Ступенчатое колесо радиуса R, масса
которого m равномерно распределена по
окружности радиуса r, катится по прямолинейному
горизонтальному рельсу, касаясь рельса ободом радиуса R=2r, имея в т.С
скорость .
Количество движения колеса равно...
1.
2. mV
3. 0
4.
- Однородный диск радиуса R и массы m вращается вокруг неподвижной оси, проходящей через т.О перпендикулярно плоскости диска, с угловой скоростью ω и угловым ускорением ε. Кинетический момент диска относительно оси вращения равен...
1. 
;
2. 
;
3. 
;
4. 
- Однородный диск радиуса R и массы m вращается вокруг неподвижной оси, проходящей через т.О и перпендикулярной плоскости диска, с угловой скоростью ω и угловым ускорением ε. Главный вектор сил инерции диска равен...
1. 
2. 
3. 
4. 0
- Однородный диск радиуса R и массы m вращается
вокруг неподвижной оси, проходящей через т.О
и перпендикулярной плоскости диска, имея ускорение в центре масс .
Тогда главный вектор сил инерции диска по модулю равен...
1. 
2. 0
3.
4.
- Однородный диск радиуса R и массы m катится
по горизонтальной плоскости без проскальзывания, имея ускорение в центре масс 
Тогда главный вектор сил инерции по модулю
равен...
1. 0
2. ma
3. 2ma
4.
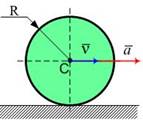
- Однородный диск радиуса R и массы m катится
по горизонтальной плоскости без проскальзывания, имея ускорение в центре масс .
Главный момент сил инерции диска относительно оси, проходящей через его центр
масс перпендикулярно плоскости колеса равен...
1. 
2. mRa
3. 
4. 
- Для механизма, представленного на рисунке, в момент времени, когда угол φ=30°, силы инерции ползунов Ф1 = Ф2 = 2Н. При использовании общего уравнения динамики, сила тяжести G1 равна (с точностью до 0,01)...
1. 5,46 Н
2. -1,46 Н
3. 0,85 Н
4. 3,15 Н
- Однородная квадратная пластина со стороной a и массой m вращается вокруг оси, перпендикулярной плоскости пластины и проходящей через середину одной из ее сторон, с постоянной угловой скоростью ω. Модуль главного вектора сил инерции этой системы Ф равен...
1. 0
2. 
3. 
4. 
- Однородный стержень CD массой m вращается вокруг неподвижной горизонтальной оси Ax, перпендикулярной стержню, с постоянной угловой скоростью ω. Размеры заданы на чертеже, массой вала можно пренебречь. Полная реакция подшипника в точке А равна RA =...
1. 
;
2. 
;
3. 
;
4. 
.
- Зубчатая передача состоит из двух колес с числом зубьев z2 = 2z1. На колесо 1 действует пара сила с моментом 10 Нм. Тогда в случае равновесия передачи модуль момента пары сил, действующей на колесо 2, равен…
1. 17
2. 25
3. 31
4. 20
5. 14
- Грузы 1 и 2 (масса груза 1 в 2 раза меньше массы груза 2) прикреплены к тросу, переброшенному через блок, ось вращения которого неподвижна и горизонтальна. Тогда ускорение грузов равно…
1. 2,94
2. 4,83
3. 3,75
4. 2,53
5. 3,27
- К горизонтальной зубчатой рейке
массой 2,5 кг приложена переменная сила F
= 9t2. Зубчатое
колесо, находящееся в зацеплении с зубчатой рейкой, имеет радиус
1. 1,5
2. 2,1
3. 0,6
4. 2,5
5. 0,9
- Оси вращения двух конических
зубчатых колес неподвижны и перпендикулярны. Радиус колеса 1 равен
1. 1
2. 2
3. 3
4. 4
5. 5
- Зубчатое колесо, находящееся в
зацеплении с зубчатой рейкой, имеет радиус
1. 20
2. 21
3. 22
4. 23
5. 24
- К звездочке 1 цепной передачи
велосипеда радиуса
1. 9
2. 10
3. 11
4. 12
5. 13
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов
