Примеры решения задач

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

Кинематика вращения тела вокруг неподвижной оси

1. Краткие сведения из теории

Уравнение вращательного движения твердого тела вокруг неподвижной оси имеет вид

. (40)

Отсчет угла ведется от выбранного начала. При этом углам, отложенным в направлении движения часовой стрелки, придается знак “минус”, а углам противоположного направления – знак “плюс”.

Угол поворота выражается в радианах. Иногда угол поворота определяется числом оборотов N. Зависимость между и N следующая .

Угловая скорость тела:

(41)

Знак производной дает возможность установить происходит ли вращение тела в положительном направлении отсчета угла поворота (знак “плюс”) или в обратную сторону (знак “минус”). Единица измерения угловой скорости – радиан в секунду (или 1/с).

Иногда угловую скорость характеризуют числом оборотов в минуту и обозначают буквой n. Зависимость между и n имеет вид

Угловое ускорение тела:

(42)

Знак производной дает возможность установить является ли вращение тела в данный момент времени ускоренным или замедленным. Если знаки и одинаковы, тело вращается ускоренно, а если их знаки различны – замедленно. Единица измерения углового ускорения – радиан на секунду в квадрате (или 1/с²).

Траекториями точек тела, не лежащих на оси вращения, являются окружности с центрами на оси вращения и радиусами, равными кратчайшему расстоянию от этих точек до оси вращения.

Модуль скорости любой точки тела, находящейся на расстоянии h от оси вращения (рис. 18), определяется по формуле

. (43)

Направлена скорость точки по касательной к описываемой точкой окружности в сторону движения.

Ускорение любой точки тела состоит из двух составляющих – вращательного и осестремительного ускорений:

Модуль вращательного ускорения точки определяется по формуле

. (44)

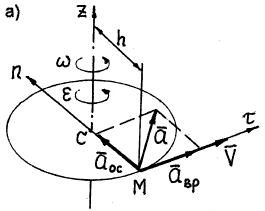
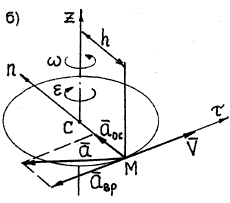
Image938.gif (3979 bytes) Image939.gif (3617 bytes)

Рис. 18

Вращательное ускорение направлено по касательной к описываемой точкой окружности в ту же сторону, что и его скорость, если вращение тела ускоренное (рис. 18, а) и в сторону, противоположную скорости, если вращение замедленное (рис.18, б).

Модуль осестремительного ускорения определяется по формуле

. (45)

Осестремительное ускорение всегда направлено по радиусу окружности от точки к центру окружности (рис. 18).

Модуль полного ускорения точки определяется по формуле

(46)

2. Основные типы задач кинематики вращения тела вокруг оси

В зависимости от того, что задано в условии задачи и что требуется определить, различают следующие два основных типа задач.

1. Исследуется движение тела в целом. В этих задачах вначале нужно получить законы (40)–(42) и, используя связь между ними, определить требуемую величину (см. примеры 17 и 18).

2. Требуется определить скорости и ускорения отдельных точек тела. Для решения задач этого типа вначале надо установить кинематические характеристики движения всего тела в целом, т.е. найти , и . После чего по формулам (43), (44), (45), (46) определить скорости и ускорения точек тела (см. пример 19).

Пример 17. Пропеллер самолета, делающий 1200 об/мин, после выключения двигателя останавливается через 8 с. Сколько оборотов сделал пропеллер за это время, если считать его вращение равнозамедленным?

Решение:

Вначале получим законы вращения пропеллера (40), (41) и (42). По условию задачи пропеллер вращается равнозамедленно, из этого следует, что

Поэтому

, (47)

(48)

Начальной угловой скоростью при замедленном вращении будет та, которую пропеллер имел до выключения двигателя. Следовательно, . В момент остановки при t₁ = 8 сек. угловая скорость тела . Подставляя эти значения в уравнение (47), получим

Отсюда

Если обозначить число сделанных пропеллером за время t₁ оборотов через N₁, то угол поворота за то же время будет равен

Подставляя найденные значения и в уравнение (48), получим

Отсюда оборотов.

Пример 18. Найти закон вращения тела вокруг оси, если известны следующие данные: угловая скорость изменяется пропорционально t², начальный угол поворота рад, для заданного момента времени t₁= 3 с угловое ускорение 1/с².

Решение:

По условию задачи модуль угловой скорости изменяется пропорционально t². Обозначая неизвестный коэффициент пропорциональности буквой k, имеем

. (49)

Найдем , беря производные по времени от обеих частей равенства (49),

Определим коэффициент k из условия, что при t₁= 3 сек. угловое ускорение 1/с²: или

Подставляя значение k в уравнение (49), получим

Учитывая, что , будем иметь

Умножая обе части этого уравнения на dt и интегрируя, находим

В начальный момент при t = 0, = 2 рад, следовательно, c = 2.

Таким образом, радиан.

Пример 19. В период разгона ротор электродвигателя вращается по закону , где t в сек, в рад.

Определить в конце 4-й секунды линейную скорость, вращательное, осестремительное и полное ускорения точки, лежащей на ободе ротора, если диаметр ротора D = 40 см.

Решение:

По заданному уравнению вращения ротора находим его угловую скорость и угловое ускорение , .

Подставляя значение t₁ = 4 сек в выражение для и , найдем

1/с,

1/с2.

Определим модули линейной скорости, вращательного и осестремительного ускорений в этот же момент времени по формулам (43), (44) и (45)

Модуль полного ускорения точки обода ротора определим по формуле (46)

3. Определение скоростей и ускорений в случаях, когда вращающееся тело входит в состав различных механизмов

Рассмотрим механизмы с поступательным и вращательным движением звеньев. Решение задачи начинают с определения скоростей точек того звена, для которого движение задано. Затем рассматривают звено, которое присоединено к первому звену и т.д. В результате определяют скорости точек всех звеньев механизма. В такой же последовательности определяют и ускорения точек.

Передача вращения от одного вращающегося тела, называемого ведущим, к другому, называемому ведомым, может осуществляться при помощи фрикционной или зубчатой передачи (рис. 19).

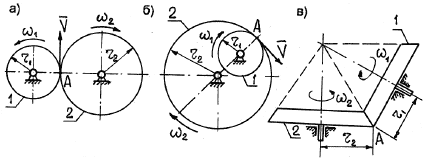
Image969.gif (7430 bytes)

Рис. 19

Во фрикционной передаче вращение передается вследствие действия силы трения в месте контакта соприкасающихся колес, в зубчатой передаче – от зацепления зубьев. Оси вращения ведущего и ведомого колес могут быть параллельными (рис. 19, а, б) или пересекаться (рис. 19, в). В рассмотренных случаях линейные скорости точек А соприкасания колес одинаковы, их модули определяются так:

. (50)

Отсюда . (51)

То есть угловые скорости колес фрикционной или зубчатой передачи обратно пропорциональны радиусам колес.

При преобразовании вращательного движения в поступательное (или наоборот) часто используют зацепление зубчатого колеса с зубчатой рейкой (рис. 20). Для этой передачи выполняется условие: .

Кроме фрикционной и зубчатой передач, существует передача вращения при помощи гибкой связи (ремня, троса, цепи) (рис. 21).

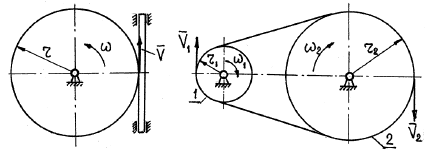
Image973.gif (5969 bytes)

Рис. 20 Рис. 21

Так как модули скоростей всех точек ремня одинаковы и ремень не скользит по поверхностям шкивов, то соотношения (50) и (51) относятся и к ременной передаче.

Пример 20. В механизме домкрата при вращении рукоятки ОА шестерни 1, 2, 3, 4, 5 приводят в движение зубчатую рейку ВС домкрата (рис. 22).

Определить скорость рейки, если рукоятка ОА делает 30 оборотов в минуту (n = 30 об/мин). Числа зубцов шестерен: z₁ = 6, z₂= 24, z₃ = 8, z₄ = 32; радиус пятой шестерни r₅ = 4 см.

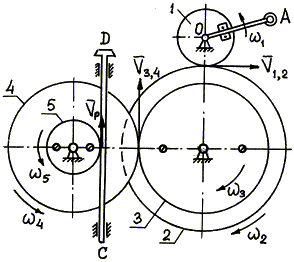
2_5.gif (8421 bytes)

Рис. 22

Решение:

Так как рукоятка ОА жестко соединена с шестерней 1, то последняя делает тоже 30 об/мин или

Модули скоростей точек соприкасания зубчатых колес 1 и 2 одинаковы для точек обоих колес и определяются по формуле (50)

Отсюда (см. также (51)).

Так как числа зубьев пропорциональны радиусам колес, то .

Отсюда

Шестерни 2 и 3 жестко соединены между собой, поэтому

Для находящихся в зацеплении колес 3 и 4 на основании (51) можно записать

Отсюда

Шестерни 4 и 5 жестко соединены между собой, поэтому

Модули скоростей точек соприкосновения зубчатой рейки ВС и шестерни 5 одинаковы, поэтому

или

Пример 21. Рейка 1, ступенчатое колесо 2 с радиусами R₂ и r₂ и колесо 3 радиуса R₃, скрепленное с валом радиуса r₃, находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис.23). Рейка движется по закону

Дано: R₂=6 см, r₂=4 см, R₃=8 см, r₃=3 см, (S - в сантиметрах, t - в секундах), А - точка обода колеса 3, t₁=3 с. Определить: , , , в момент времени t = t₁.

Указания. Пример 21 - на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что, когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы, при этом считается, что ремень по ободу колес не скользит.

Решение:

Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса R₁), через V₁, а точек, лежащих на внутренних ободах (радиуса r₁), через U₁.

1. Зная закон движения рейки 1, находим ее скорость:

. (52)

Рис. 23

Так как рейка и колесо 2 находятся в зацеплении, то V₂=V₁ или . Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, или . Из этих равенств находим: